基于MATLAB软件对ULF车辆门架式转向架径向机构通过曲线的运动仿真分析
2016-06-01张德乾王伯铭李天一
张德乾 王伯铭 曹 恺 李天一
(西南交通大学机械工程学院,610031,成都∥第一作者,硕士研究生)
基于MATLAB软件对ULF车辆门架式转向架径向机构通过曲线的运动仿真分析
张德乾王伯铭曹 恺李天一
(西南交通大学机械工程学院,610031,成都∥第一作者,硕士研究生)
摘 要介绍了ULF车辆的门架式转向架的结构组成,分析了径向调节机构的工作原理和特点。利用Matlab软件对转向架径向调节机构进行数学建模和运动仿真,重点分析不同速度和不同曲线半径条件下前后车轮的摇头角位移、摇头角速度和摇头角加速度。通过对比分析,认为径向调节机构可以减小轮缘冲角,使门架式转向架通过曲线性能良好。
关键词低地板轻轨车辆;门架式转向架;径向调节机构;运动分析;Matlab仿真
Author's address College of Mechanical Engineering,Southwest Jiaotong University,610031,Chengdu,China
ULF车辆为奥地利SGP公司生产的超低地板轻轨车辆,由于采用了门架式转向架,车辆地板面在车门入口处距轨面的高度只有152 mm,另一侧高度为197 mm。车组由5辆或7辆短车体通过铰接形式连接。列车总长24 m(5辆)或35 m(7辆),两铰接端的间距为5 630 mm[1]。
ULF车辆采用了独特的门架式单轴迫导向径向转向架技术,如图1所示。其中,牵引电机单元(包括三相异步电机、制动盘和齿轮传动装置)竖向悬挂,二系悬挂与车体中部连接。转向架被安放在两车体之间的连接处,车体之间用铰接装置连接,允许模块之间的相对转动[2]。由于门架式转向架属于径向转向架,当车辆进入曲线时,铰接在一起的车体会产生相对转动,从而带动连杆机构动作,拉动转向架趋于径向位置。
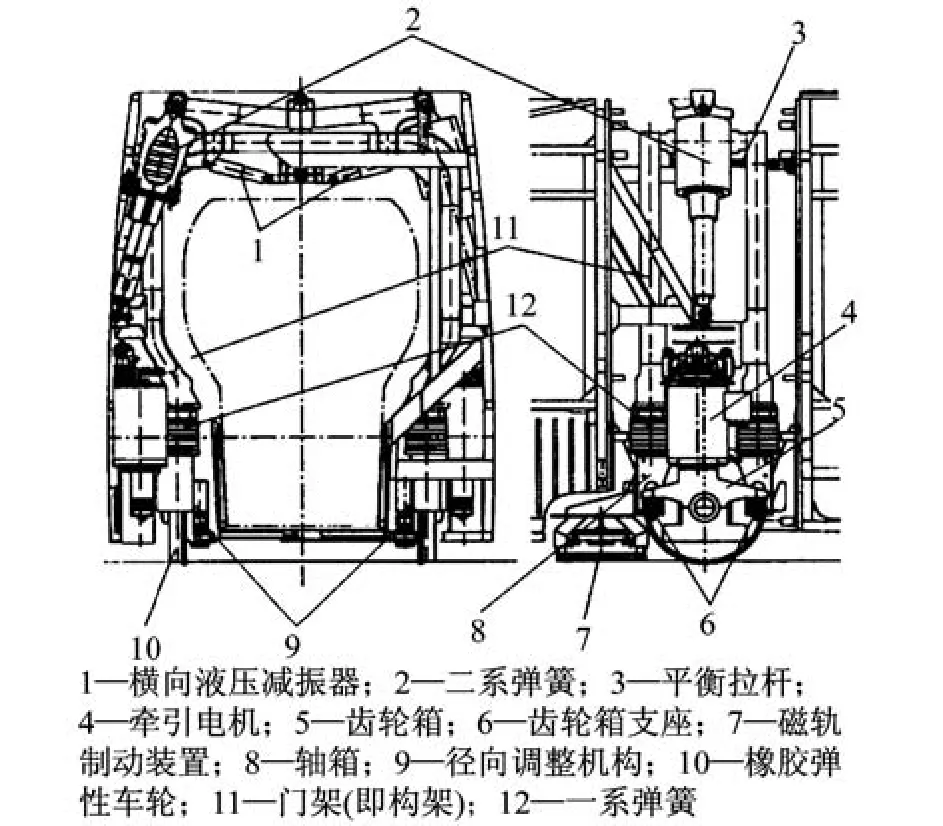
图1 ULF车辆门架式转向架
1 门架式转向架径向调节机构的基本原理和特点
1.1径向调节机构的基本工作原理
ULF车辆的头车和中间车体之间的门架式转向架径向调节机构如图2所示。通过曲线时,车体2和车体3相对回转,通过对称控制装置带动转向架2径向转动,并通过径向调节机构促使前车转向架1径向调节。该转向架径向调节机构主要有三个功能:①通过对称控制装置将相邻车体间的相对摇头角位移传递到跟随转向架2的左右车轮;②通过径向调节机构将跟随轮组摇头角位移传递到前车转向架车轮,使前、后转向架车轮发生径向调节;③左、右车轮横向控制机构使同一转向架具有相同的摇头角位移[3]。
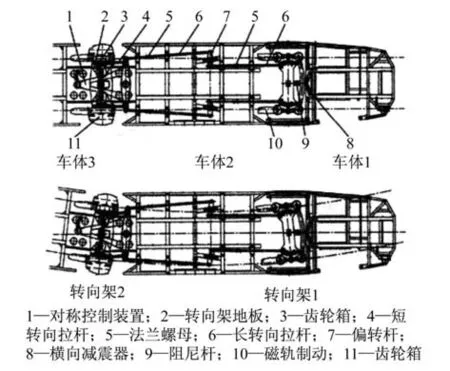
图2 门架式转向架径向调节机构
1.2径向调节机构的主要特点
(1)转向架两侧的车轮为独立驱动。两个车轮借助对称控制装置各自与车体耦连在一起,当车辆通过曲线时能够自动调节到曲线半径方向,使左右车轮保持平行。
(2)前部和后部车轮通过横向控制机构与相邻的门架连接架连接在一起。横向控制机构允许这些车轮(尽管它们本身不受约束)调节到曲线半径方向,而左右车轮保持平行。
2 径向调节机构的模型简化和运动方程分析
2.1径向调节机构模型简化
为了简单准确地分析门架式转向架径向调节机构,可将整个机构简化为图3所示的机构模型。图中L1、L2、L3、L4、L5、L6、L7、L8、L9分别为杆件1、杆件2、杆件3、杆件4、杆件5、杆件6、杆件7、杆件8、杆件9的长度。径向调节驱动由杆件1输入。为了更好地满足车辆实际运行的需要,径向调节机构整体呈对称结构布置。

图3 ULF车辆门架式转向架径向调节机构简图
当车辆在直线运行时,机构中杆件1平行于杆件5,杆件4平行于杆件7,从而保证了前、后车轮轴平行并且垂直于轨道中心线稳定向前运行;当车辆进入曲线段时,由于车体与车体之间的相对转动,在对称控制装置的作用下,车体间的转动被传递到后车车体转向架,迫使后车车轮径向回转,通过与之铰接的径向调节机构进一步推动前车车体转向架车轮向曲线径向方向调整。即图3中,杆件1绕铰接点A回转从而带动杆杆件5绕铰接点G回转。
2.2机构自由度确定
径向调节机构中的活动构件数n=9,低副数Pl=13,高副数Ph=0,则由平面一般机构自由度的计算公式F=3n-2Pl-Ph,可得到径向调节机构自由度F=1。
由于机构自由度=原动件数目=1,所以机构具有确定的运动轨迹。
2.3机构位置分析
对杆件1、2、3所组成的RRRⅡ级杆组进行分析[4]。
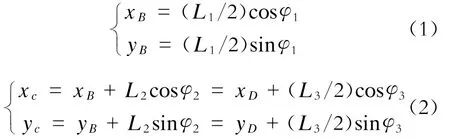
式中:

式中:
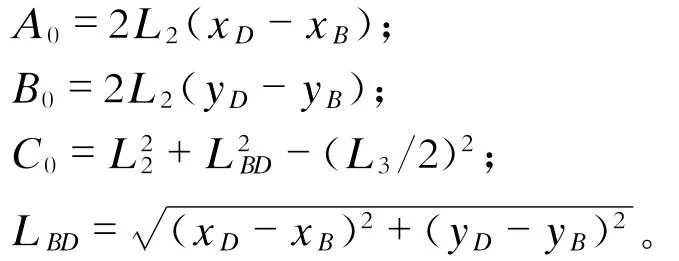
解式(3)可得:
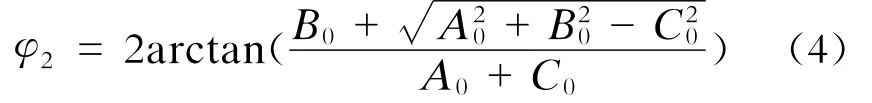
将结果代入式(2)可求得φ3。
由于杆件6刚度大,可将G点看成不动点,这样只需对杆件3、4、5所组成的RRRⅡ级杆组进行分析。式中:

φ4——L4与水平方向的夹角;
φ5——L5与水平方向的夹角。
将式(6)移项后平方相加,消去φ5后可得:
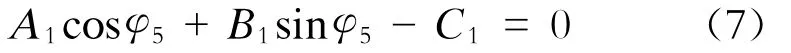
式中:
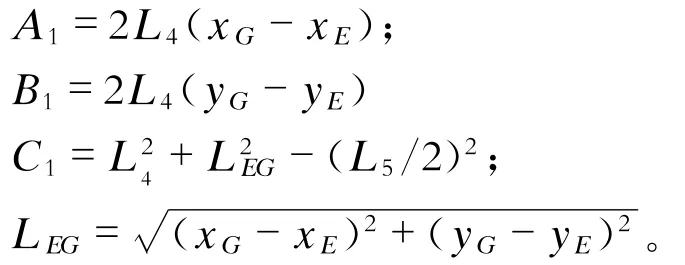
解式(7)可得:
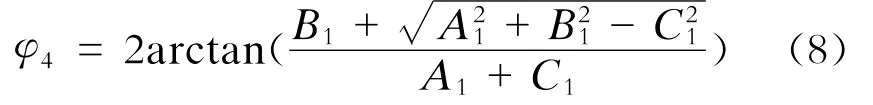
将结果代入式(6)可求得φ5。
2.4机构角速度分析
将式(1)对时间t求导,可得B点速度:
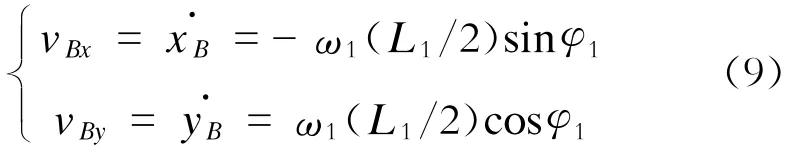
式中:
ω1——L1的转动角速度。
将式(2)对时间t求导可得:
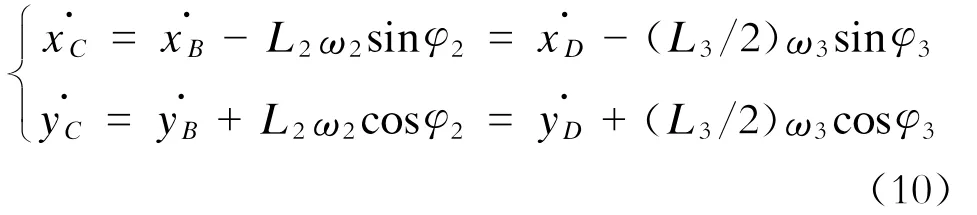
式中:
ω2——L2的转动角速度;
ω3——L3的转动角速度。
由式(9)、(10)联合可得:
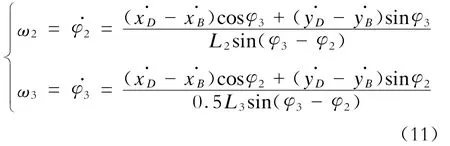
将结果代入式(10)可得C点速度。
将式(5)对时间t求导,可得E点速度:
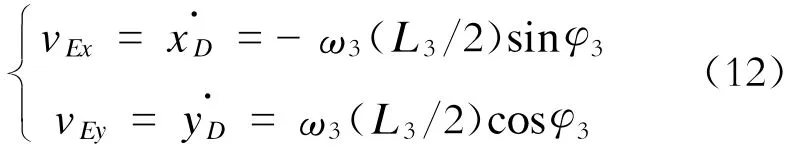
将式(6)对时间t求导可得:
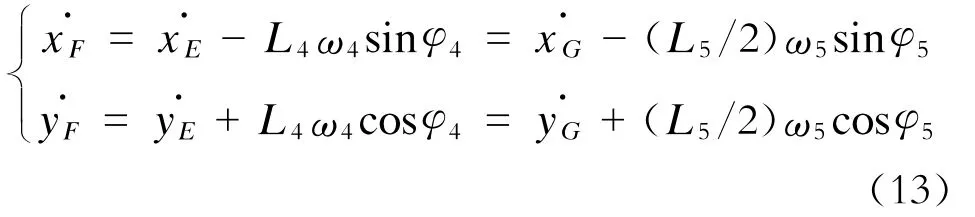
式中:
ω4——L4的转动角速度;
ω5——L5的转动角速度。
由式(12)、(13)联合可得:

将结果代入式(13)可得F点速度。
2.5机构角加速度分析
将式(11)、(14)分别对时间t求导得:
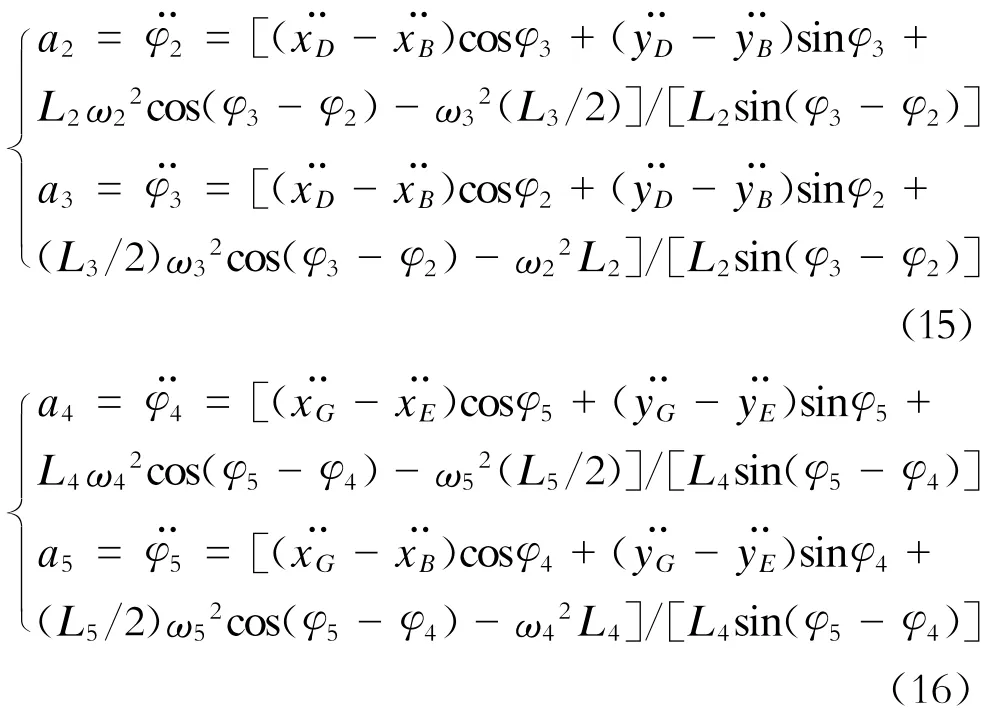
式中:
a2——L2的角加速度;
a3——L3的角加速度;
a4——L4的角加速度;
a5——L5的角加速度。
根据式(15)、(16),可得C、F点的加速度为:
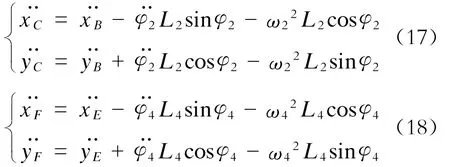
3 径向调节机构通过曲线时的运动学分析
3.1机构模型参数初始化
(1)关键点位置初始化,如表1所示。
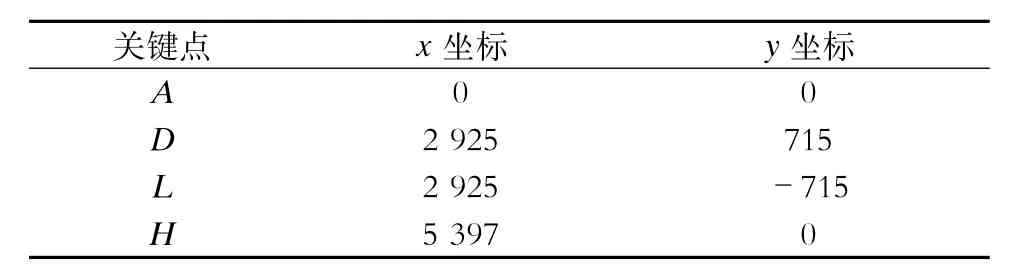
表1 关键点坐标 mm
(2)关键杆长初始化,如表2所示。

表2 关键杆长
3.2车辆通过带缓和曲线的圆曲线径向调整角的确定
目前,国内外传统铁路和高速铁路中大部分采用三次抛物线形的缓和曲线[5]。三次抛物线形缓和曲线的方程为:

式中:
R——圆曲线半径;
L——缓和曲线长度。
抛物线上任意一点的切线偏角或调整角β为:
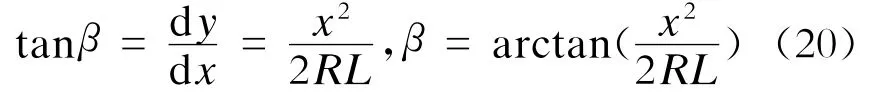
由于β变化比较小,所以可进行以下的近似计算:
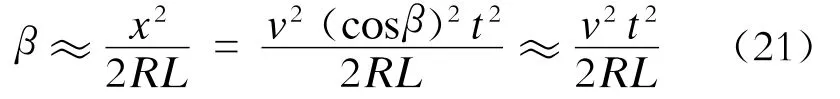
3.3不同半径条件下的机构运动仿真分析
根据我国颁布的《城市快速轨道交通工程项目建设标准》,地铁和轻轨等不同轨道交通正线最小曲线半径分别为:A型车300~500m;B型车250~300m;C型车50~100m。ULF车辆属于C型车,故分别选取50m、100m半径的曲线进行径向调节机构的运动学分析。
列车速度v=40km∕h,缓和曲线长度L= 40m,圆曲线半径R分别为50m、100m。利用Matlab软件进行径向调节机构的数学建模和软件编程,通过图4所示的流程图,仿真了不同曲线半径下机构的运动学性能。
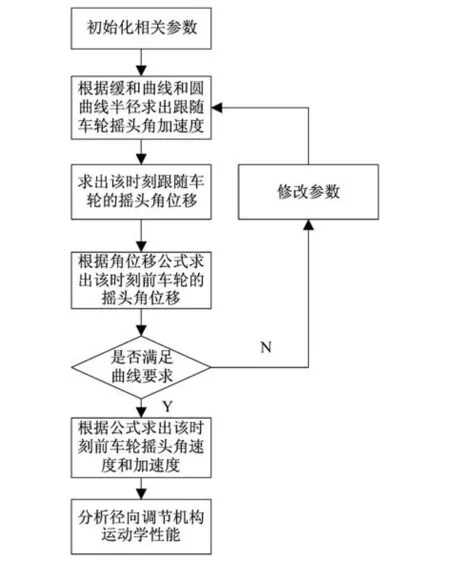
图4 不同曲线半径下Matlab软件仿真流程图
图5为前后车轮在不同曲线半径下的摇头角位移曲线。可以看出,机构的最大径向调整角与曲线半径有关。随着曲线半径的增大,最大径向调整角变小,车轮径向调节的趋势逐渐变缓;半径越大,达到最大径向调整角的时间越长。当曲线出现拐点时,说明机构达到了最大调整角,即车辆已经完全进入曲线,并且在后续一段时间内该角度保持不变。在两种曲线半径下,ULF车辆前后车轮都能在极短的时间内完成径向调节,说明机构的运动学性能良好。
图6为前后车轮在不同曲线半径下的摇头角速度曲线。可以看出,随着曲线半径的增加,前后车轮的径向调节速度变缓。从时间原点开始,车轮径向调节速度从0开始匀速上升,说明机构没有滞后性,响应灵敏平稳。当曲线出现拐点时,说明机构达到了最大调整角,即车辆已经完全进入了曲线,由于此时摇头角保持不变,所以摇头角速度变为0。
图7为前后车轮在不同曲线半径下的摇头角加速度曲线。可以看出,随着曲线半径的增加,车轮的摇头角加速度变小,曲线出现拐点的时间度变长,即达到机构最大调整角的时间增加。当曲线出现拐点时,说明车辆已经完全进入曲线,摇头角角度保持不变,摇头角加速度变为0。在出现拐点前曲线平稳,说明机构径向调节平稳。
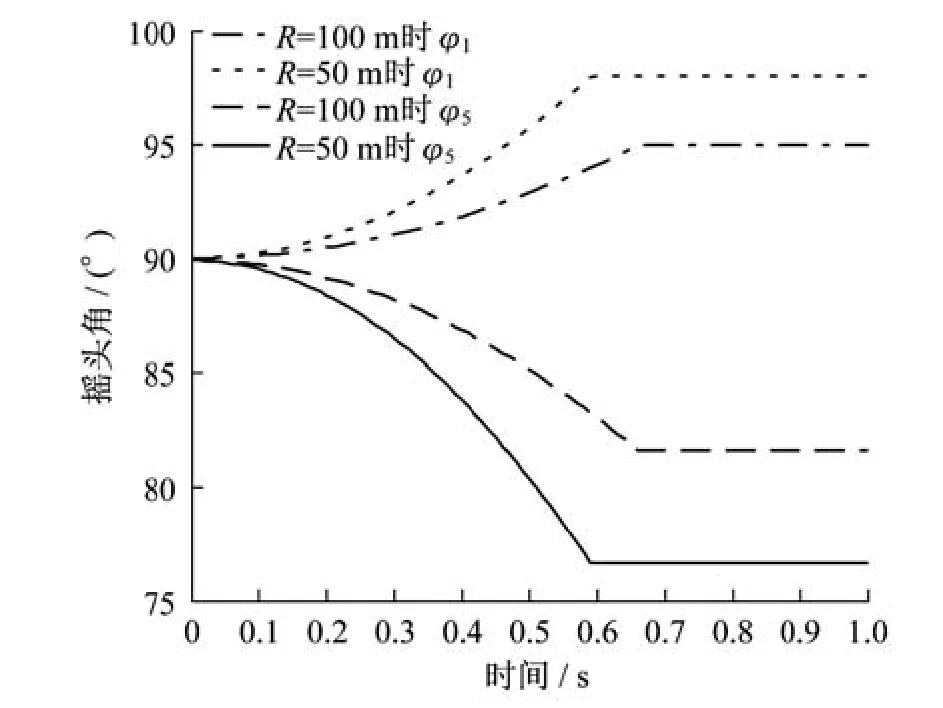
图5 不同曲线半径下前后车轮摇头角位移曲线
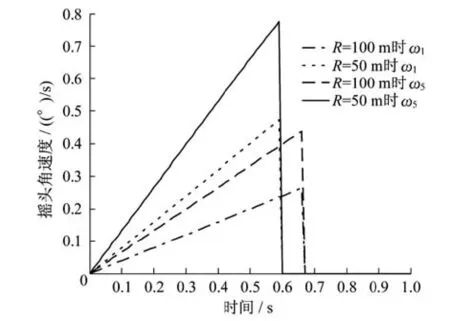
图6 不同曲线半径下前后车轮摇头角速度曲线
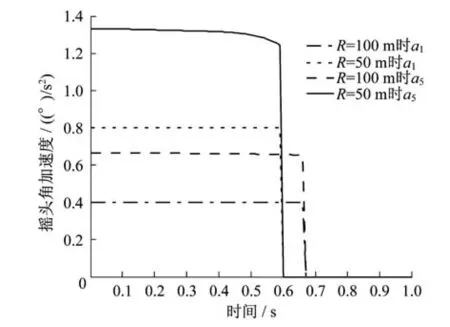
图7 不同曲线半径下前后车轮摇头角加速度曲线
3.4不同速度条件下的机构运动仿真分析
基本运动工况为:L=40 m,R=50 m,列车速度v分别为30 km∕h、40 km∕h。
通过Matlab机构仿真,得出了不同速度时机构的运动学性能。不同速度条件下径向调节机构的仿真流程如图8所示。

图8 不同速度条件下Matlab仿真流程图
图9为前后车轮在不同速度条件下的摇头角位移曲线。可以看出,车轮速度越大,径向调节的趋势越大,到达最大调整角的时间越短,但机构的最大径向调节角度与车轮速度无关。当曲线出现拐点时,说明机构达到了最大调整角,即车辆已经完全进入曲线,这时摇头角保持不变。两种速度下,车轮完成径向调节的时间都比较短,说明机构响应灵敏、性能良好。

图9 不同速度下前后车轮摇头角变化曲线
图10为前后车轮在不同速度条件下的摇头角速度变化曲线。从中可看出,随着车轮速度增加,前后车轮的径向调节速度也逐渐变大。从时间原点开始,车轮径向调节速度从零匀速增加,说明机构反应灵敏,没有滞后性。当曲线出现拐点时,说明机构达到最大调整角,这时车辆已经完全进入曲线,摇头角保持不变,所以摇头角速度变为0。
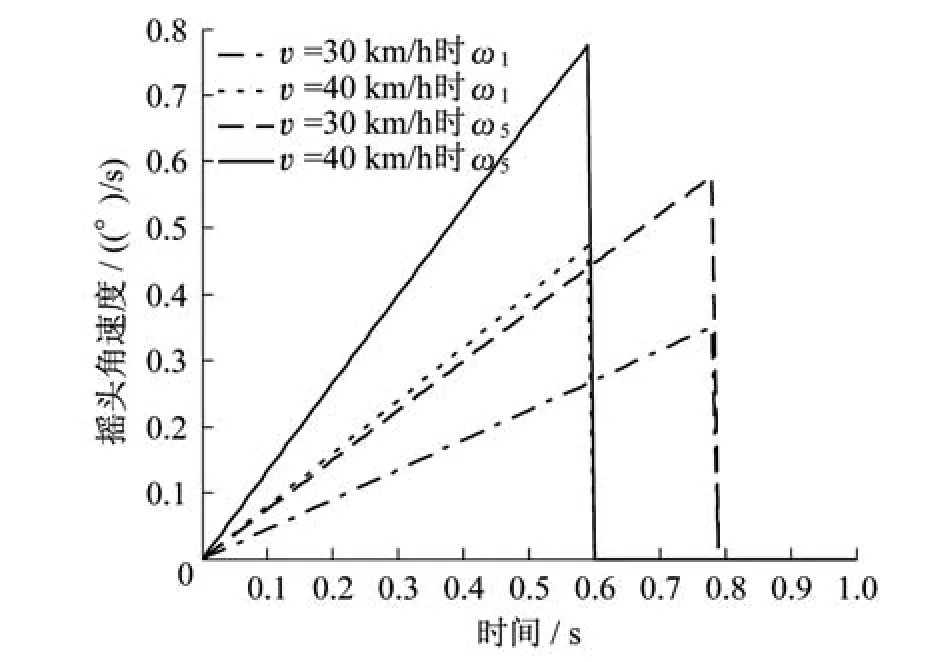
图10 不同速度下前后车轮摇头角速度变化曲线
图11为前后车轮在不同速度条件下的摇头角加速度变化曲线。从中可以看出,随着车轮速度增加,车轮的摇头角加速度逐渐变大,曲线出现拐点的时间缩短,即到达机构最大调整角的时间缩短。当曲线出现拐点时,说明车辆已完全进入曲线,摇头角角度保持不变,所以摇头角加速度变为0。在出现拐点前曲线平稳,说明机构径向调节平稳。
4 结论
(1)径向调节机构的最大调整角与车轮速度无关,但与曲线半径大小有关。
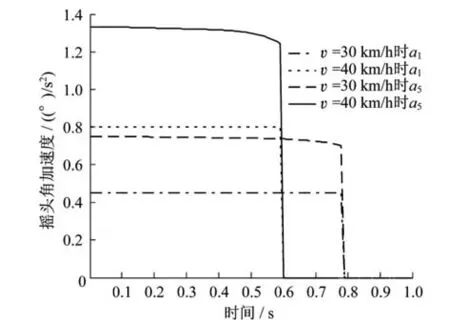
图11 不同速度下前后车轮摇头角加速度变化曲线
(2)径向调节机构在不同曲线半径和不同速度条件下反应灵敏,没有时间的滞后性,可以快速实现车轮曲线导向。
(3)在相同车轮速度下,曲线半径越大,机构运动学性能越好;在相同的曲线半径下,速度越小,机构运动学性能越好。
(4)径向调节机构可以明显减小轮缘冲角,从而降低车轮受力,可有效提高车辆的曲线通过性能。
参考文献
[1] 王欢,戴焕云,池茂儒.国外100﹪低地板轻轨车辆发展概述[J].国外铁道车辆,2012,49(2):1.
[2] 王欢,戴焕云,关庆华.100﹪低地板轻轨车辆导向结构分析[J].铁道车辆,2009(9):12.
[3] HONDIUS H.Low-floor development out of control[J]. Railway Gazette International,1991(11):793.
[4] 于红英,唐德威,王建宇.平面五杆机构运动学和动力学特性分析[J].哈尔滨工业大学学报,2007,39(6):940.
[5] 王国栋,马俊海.铁路三次抛物线缓和曲线的计算[J].交通科技与经济,2011,13(1):13.
Simulation Analysis of the Negotiation Curve Motion of ULF Portal Bogie Based on MATLAB
Zhang Deqian,Wang Boming,Cao Kai,Li Tianyi
AbstractThe structure of ULF portal bogie is introduced,its working principle and structure of the radial adjustment mechanism are analyzed.Then,mathematical modeling and motion simulation are conducted for radial bogie regulatory agencies by using Matlab software,the front and rear wheels'head shaking angular displacement,the angular velocity and angular acceleration under different velocities and curve radius are analyzed with particular emphasis. Through comparative study,it can be concluded that the radial adjustment mechanism can reduce the rim angle of attack to ensure good performance of the portal bogie negotiation curve.
Key wordslow-floor ULF vehicle;portal bogie;radial adjusting mechanism;motion analysis;Matlab simulation
中图分类号U 270.331
DOI:10.16037∕j.1007-869x.2016.01.006
收稿日期:(2014-03-22)