微重力下低温液氧贮箱热分层研究

刘 展 孙培杰 李 鹏 厉彦忠 晋永华

(1西安交通大学能源与动力工程学院 西安 710049) (2上海宇航系统工程研究所 上海 201108)

微重力下低温液氧贮箱热分层研究

刘 展1孙培杰2李 鹏2厉彦忠1晋永华1

(1西安交通大学能源与动力工程学院 西安 710049) (2上海宇航系统工程研究所 上海 201108)

为研究微重力下，在轨运行低温液氧箱体内部流体温度场分布，建立了相关数值模型，考虑了气液相变以及各空间辐射热流的影响。计算结果表明：当g为0 g0时，表面张力驱使液相包裹气枕，并将球形气枕挤出壁面。由于箱内没有自然对流，箱体壁面流体会出现局部过热。当g增加到10-6g0时，表面张力作用仍较为明显。箱体内部物理场分布与0 g0工况大致相同。当g增加到10-5g0时，液相已不能完全包裹气相，气相区一直与箱体顶部接触。当g增加到10-4g0时，此时箱体内部自然对流已十分明显，气相区大致呈带状，并与顶部壁面有较大的接触面积。短时间内，自然对流可及时将外部漏热带入箱体内部。另外，箱体压力随时间增长呈先降低后逐渐升高的趋势。重力越小，箱体压力也越小。最后通过对比还发现，初始边界条件设置对箱体内部物理场有较大的影响。

微重力 低温液氧箱体 热分层 空间辐射

1 引 言

低温推进剂贮箱在轨运行期间将受到微重力及表面张力的共同影响。由于微重力效应所带来的热对流将逐渐减弱，由表面张力驱动所引起气液界面面积增加的影响[1-2]逐渐增强。因此研究微重力下，低温箱体内部流体温度分层意义重大。

目前来看，有关低温箱体分层增压的研究，研究人员主要采用了理论分析模型[3-5]以及数值模拟方法[6-11]进行了研究。理论模型中，零维模型由于模型简单计算方便，应用较广泛。但该模型由于因素考虑不全面，限定性假设较粗糙，在预测箱体压增及温度场时往往与实际情况偏离较大；已有的CFD模型在一定范围内能够较好预测箱体增压过程。在已有的文献中，研究人员大都只针对某一特定重力水平下，研究了低温箱体的增压分层现象，并未考虑对不同重力水平对该过程的影响，为此有必要对不同重力水平下在轨运行低温贮箱分层增压过程进行研究。本文针对某一设计低温推进剂箱体，采用VOF模型研究其在不同微重力条件下的分层增压过程。相关研究结果可为低温贮箱在轨增压设计提供技术参考。

2 研究对象

以某一低温液氧贮箱为例，对其在轨运行过程进行数值模拟。液氧箱体包括筒段以及前后底椭球形封头。其中筒段直径2 000 mm，高1 095 mm；上下底封头高500 mm。贮箱壁面为铝合金材料，厚4.0 mm，金属壁密度取2 800 kg/m3，导热系数159 W/(m·K)，比热容830 J/(kg·K)。箱体外部包裹发泡+多层绝热材料。发泡层厚20 mm，绝热材料导热系数约0.03 W/(m·K)，密度取40 kg/m3，比热容为1 470 J/(kg·K)。多层绝热材料厚10 mm，其密度约50 kg/m3，比热容为1 000 J/(kg·K)，导热系数8×10-4W/(m·K)。初始液位高度1 995 mm。另外，本过程为箱体自增压过程，箱体初始压力为0.35 MPa。

3 空间热辐射模型

在轨运行期间，低温液氧箱体受到各种空间辐射的影响。在不同空间辐射热流中，太阳直射辐射、地球反照辐射、地球红外辐射以及空间黑背景辐射[12]为主要辐射方式，需着重考虑。

3.1 太阳辐射

从近地轨道至地球同步轨道的高度内，太阳光被认为是均匀的平行光束，其辐射强度为一个太阳常数S(取1 414W/m2)。低温箱体外表面投影面积A上所收到的太阳辐射外热流为：

(1)

式中：φ1为太阳辐射角系数；q1为太阳辐射外热流，W;A为投影面积，m3。

3.2 地球反照外热流

假设地球为漫反射体，对太阳辐射的反射遵守兰贝特定律且各处均匀，反射光谱与太阳光谱相同，反照率以平均反照率ρ表示，本文取ρ=0.3。则地球表面对箱体外表面投影面积的地球反照辐射外热流为：

(2)

式中：φ2为地球反照角系数；q2为地球反照外热流，W。

3.3 地球红外辐射热流

假设地球是一个均匀辐射的热平衡体，并且地球表面上任一点红外辐射强度相同。低温箱体外表面投影面积收到整个地球表面AE的红外辐射外热流为：

(3)

式中：φ3为地球红外角系数，该系数跟地球光照部分以及箱体与地球间的相对位置有直接关系，计算十分复杂；q3为地球红外辐射热流,W。对于近地运行低温箱体来说，由于地球反照外热流在箱体所接收的总空间辐射外热流中所占比例较小，因此本处为了简化φ3的计算，采用如下近似。

(4)

式中：ψ为相角。

3.4 空间黑背景辐射

由于空间深空背景温度较低，约4K左右，因此低温箱体将向空间黑背景辐射冷量。该部分冷量采用Stephen-Boltzmann定律确定。

(9)

式中：ε为贮箱外壁发射率取0.7，q4为箱体壁面向外部环境辐射热流量，W;Tw为箱体壁面温度，K;At为箱体外表面积,m2。

至此，低温液氧箱体所接受的总辐射热流量qt为

(10)

式中：α为贮箱外壁吸收率，取0.4。

该热流是随时间以及空间逐渐变化的。因此在计算模拟中，需将此部分热流通过自定义程序输入计算模型，并作为热边界条件，以实现在轨阶段对各空间漏热的考虑。

4 计算设置

采用Gambit 2.4.6前处理器对低温液氧箱体进行分区网格划分。箱体筒段划分结构网格，上下底封头采用非结构网格。金属壁面以及绝热层分别划分网格，紧贴壁面处采用边界层网格。采用二维轴对称面网格来预测该物理过程。通过计算对比最终选定计算网格数约为30 298。

采用Fluent15双精度求解器对不同过程进行非稳态数值求解。计算时间步长为0.001 s。选用VOF两相流模型计算箱体压增分层过程。采用标准k-ε模型模拟箱体内部流体与壁面间流固耦合作用。压力项采用PRESTO格式，压力速度耦合项选用PISO算法，其他参量均采用二阶迎风格式。气相采用理想气体模型；液相密度仅随温度变化，其他参数均参考物性软件NIST。在微重力条件下，表面张力作用明显。因此，模型中激活表面张力选项，选取连续表面力模型，接触角取10°，表面张力取0.013 473N/m。

在外部漏热下，气液界面会发生传热传质过程。计算过程中，可通过对比网格温度Tcell与饱和温度Tsat的相对大小来作为相变发生的判据[13-14]具体如下：

当Tcell≥Tsat时，液体蒸发

(11)

当Tcell

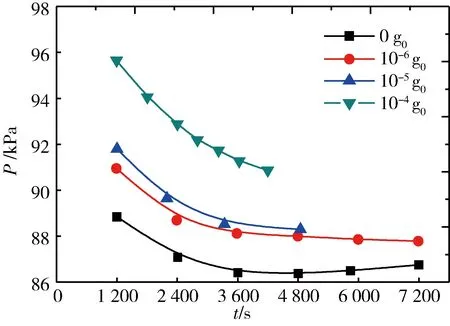
(12)

5 计算结果分析

分别对两种工况下低温氧箱分层增压过程进行对比分析：工况1中假定箱体筒段与前后底均为辐射边界条件，辐射热流为箱体所接受外部热流的平均值；工况2中假定箱体筒段与后底为辐射边界条件，箱体前底设为定温边界条件，温度为110 K。两工况初始状态均相同，仅有前底边界条件不同。

5.1 工况1

通过考虑空间太阳辐射、地球红外、反照辐射和空间冷背景辐射的影响，并根据空间辐射换热模型进行计算，箱体各壁面辐射热流在8—15 W/m2范围内。本处对不同工况边界热流均取15 W/m2。由于壁面温度高达200—300 K，为方便对比，不同时刻不同重力下，箱体内部显示的温度分布均设定为89—90 K。另外，相图中红色区域为气相，蓝色区域为液相。

通过对初始液位为1 995 mm的低温液氧贮箱进行数值模拟，详细计算结果如下。图1展示了在所有边界均设置为辐射热流边界的条件下，不同重力水平、不同时刻低温液氧箱体内部温度场及相分布。图1a给出了0 g0工况下，1 200、2 400以及3 600 s三时刻下，液氧箱体气液相分布以及温度分布。可以看出，在没有重力的情况下，表面张力起主导作用。气液界面由最初的水平界面先变为曲面，然后会逐渐变为球面。当时间为1 200 s时，在表面张力的作用下，气相逐渐被液相包裹，但此时气枕仍附着在箱体壁面。随着时间的增加，球形气相区逐渐脱离壁面，在惯性力的作用下，沿箱体旋转轴向下运动。在1 200 s时，由于气相温度较高，并且气相处于箱体顶部，受箱体形状以及球形气相的影响，与气相所接触的液相温度分布并不均匀。气相区以下，受气相向液相的导热影响，该部分温度分层较规律。在2 400 s时，气相区已脱离壁面，向箱体底部运动，此时整个气相区仍大致保持球形。球形气枕经过的地方会造成液相温度分布的不均匀性。气相以下的液相区受壁面导热以及气相导热的影响，形成了近似半椭圆的温度分布。当时间为3 600 s时，受惯性力、表面张力以及其他扰动的影响，气枕开始变形，并且部分气相开始被液相撕裂成小的气泡。此时箱体内部温度分布已比较混乱，气相以及壁面两个高温区均向液相导热。由于与壁面所接触的液相直接接受壁面漏热，此时没有自然对流，热量会集中在箱体壁面，造成液相核态沸腾。由于大部分流体仍具有一定的过冷度，即使气泡产生也会被液相冷却掉，所以图中并没有发现壁面有气泡产生，但紧贴箱体壁面一圈，液相温度均出现局部过热。

当重力水平由0 g0增加到10-6g0时，在表面张力作用下，液相仍可以将气枕包裹成球形。如图1b所示，气枕在1 200 s以及2 400 s时，均为球形，并且紧贴箱体顶部壁面。在3 600 s时，气枕脱离了壁面向箱体底部运动。 而在0 g0工况下， 2 400 s时气枕已脱离了壁面。这说明当重力水平增加时，气枕脱离壁面所需要的时间是逐渐增长的。在10-6g0工况下，1 200 s时箱体气液相分布以及温度分布与0 g0工况基本一致。当时间增加到2 400 s时，在气相以及壁面的漏热下，气相下部液相温度均呈现近似半椭球型线分布。在3 600 s时，由于气相向下运动，与气相接触的上下部液相温度扰动增加。并且随着时间的增长，箱体壁面流体也出现局部过热的现象。

图1 工况1，不同重力水平不同时刻箱体内部流体温度及相分布图Fig.1 Case1，liquid temperature and phase distribution over timein different microgravity

图1c展示了10-5g0工况下，不同时刻流体相分布以及温度分布图。该工况与上述两工况最明显的不同是：在微重力与表面张力的共同作用下，液相已不能将气枕包裹成球形，此时气枕近似椭球型。通过对该工况计算3 600 s还发现，气枕在这一过程中始终未脱离箱体顶部，气相区域始终与箱体顶部接触。出现这种现象的原因是，当重力为10-5g0时，其所引起的浮力大小已可以与表面张力相匹敌，表面张力已不能使气相变成球形或脱离壁面。从流体温度分布上来看， 本工况1 200 s时与之前工况没有太大区别。2 400 s时温度分布与10-6g0工况下也较为相似。而3 600 s时箱内流体温度分布与10-6g0工况有较大的区别，但却与本工况2 400 s时温度分布较为相近。两时刻所不同的是，3 600 s时箱体壁面流体温度出现局部过热。

10-4g0工况下，箱体内部流体相分布以及温度分布可参见图1d。该工况与前3种工况均不同。首先，气枕只有边缘区被液相包围，大致呈条带型，并且没有脱离壁面。计算3 600 s，气枕形状没有发生明显变化。这说明10-4g0微重力已开始起主导作用，极大抑制了液体表面张力的影响。再者箱体内部温度均呈现环状分布。这主要是由于在10-4g0工况下，受壁面加热的影响，热流体在浮升力的驱动下向上运动，当运动到箱体顶部或气枕区时，热流体折返回来，并向下运动，由此形成环流。具体变化可参考图2所展示箱体内部速度场分布。从中可以看出，气枕下部的折回流体仍具有较大的速度。另外，在自然对流循环的影响下，壁面漏热被及时带到箱体内部，箱体壁面处流体没有出现局部过热的现象。但随着时间的增长，当自然对流不能完全带走外部漏热时，壁面仍将有局部过热现象的出现。

图2 10-4g0中箱体内部速度场分布Fig.2 Velocity field distribution inside tank in 10-4 g0 microgravity

图3展示了工况1条件下，不同重力水平下箱体压力变化。从中可以看出，不同重力水平下，箱体压力随时间大致呈现出先逐渐降低，然后再缓慢升高的趋势。出现这种现象的原因是由于气相温度比液相温度高，其将向低温液体传递热量。气枕被液体冷却，以致于气相压力出现逐渐降低。但随着气枕向箱体底部运动或长时间的集聚在箱体顶部，气相会被被撕裂或冷凝，此时气相被液相压缩，所以气枕压力又出现逐渐升高的变化。另外，从图中还可以看出，当重力水平由10-4g0减小到0 g0时，箱体压力呈逐渐减小的态势。这主要是因为，重力水平越小，在表面张力作用下，液相越能包裹更大的气相区域，如在10-6g0以及10-5g0下，液相已全部包裹气相。当气相与液相接触表面较大时，气相被液相冷却的程度越大，气相压力降低也越大。因此也就出现重力水平越小，箱体压力越小的趋势。

图3 工况1，不同重力水平下箱体压力变化Fig.3 Case 1, pressure changes inside tank indifferent microgravity

5.2 工况2

为与工况1方便对比，工况2箱体筒段以及后底壁面热流仍取15 W/m2。前底采用定温边界，温度110 K。计算结果中，气液相温区仍控制在89—90 K内。

图4展示了在工况2条件下，不同重力水平、不同时刻低温液氧箱体内部温度场及相分布。从图4a所展示的0 g0下气液相分布以及流体温度分布可知，在前2 400 s时，物理场分布与工况1大致相同，而到3 600 s时，两工况出现了较大的差异。工况2中，被液相包裹的气相向下运动到一段距离之后，在惯性力以及表面张力的作用下，开始向箱体顶部运动。这种现象在工况1中也有出现，但时间较短。整体上，气相是向箱体底部运动的，但在运动过程中伴随着气相形状以运动方向的变化。对工况2进行更长时间的监测发现，气相也会向箱体底部运动。

图4 工况2，不同重力水平不同时刻箱体内部流体温度及相分布图Fig.4 Case2，liquid temperature and phase distribution over timein different microgravity

图4b与图4c所展示的10-6g0以及10-5g0下的物理场分布与工况1条件下的物理场分布大致相同。只不过工况2条件下，与箱体筒段以及后底所接触流体出现了更大区域的高温区。箱体前底由于设置定壁面边界，漏热热流相对较小，与其接触的流体并没有出现大面积的局部过热。

图4d展示了工况2条件下，10-4g0重力水平下的箱体内部相分布及温度场分布云图。对比两工况发现，箱体内部气液相分布大致相同，温度分布也基本一致。但工况2下的温度场发展明显晚于工况1下的温度发展，并且与箱体筒段以及后底所接触流体均出现了不同程度的局部过热。分析原因有可能是箱体壁面边界条件设置的原因。由于边界条件初始设置不均匀，前底与筒段热流边界过渡不顺畅，导致箱体筒段热流过于集中，并在此处出现了局部过热。再者通过计算3 600 s，工况2箱体内部自然对流发展仍处在箱体底部；而工况1中，已发展到箱体中部。初始边界条件的设置影响了工况2箱体内部自然对流的发展。

图5展示了在工况2条件下，不同重力水平下箱体压力变化。可以看出，工况2条件下，箱体压力变化与工况1大致相同。受表面张力以及气泡运动的影响，随着时间的增加，箱体压力呈现先减小后逐渐增加的变化。箱体压力随着重力水平的减小也逐渐减小。

图5 工况2，不同重力水平下箱体压力变化Fig.5 Case 2, pressure changes inside tank indifferent microgravity

两种工况下，各不同重力不同时刻下，液氧箱体内部物理场分布大致相同，但由于初始设置不同，工况1前底漏热热流要高于工况2漏热热流，导致两工况的物理场还是出现了区别。由于工况1中壁面漏热整体较大，该工况下箱体内部温度分布整体较高，并且在大热流下，气泡运动以及自然对流发展都较快。

6 结 论

针对在轨运行低温液氧箱体，本文详细考虑了各种空间辐射热流的影响，数值研究了低温箱体内部气相形态变化以及箱内温度场分布。对不同重力水平进行3 600 s计算发现：当重力水平为0 g0时，表面张力其主导作用，液相会逐渐包裹气相，并将气相挤出壁面。球形的气相在惯性力作用下向箱体的底部运动，运动过程中伴随着气泡形状的变化以及被液相撕裂出小气泡的现象。由于此时箱体内部没有自然对流，一段时间以后，箱体壁面流体会出现局部过热。当重力水平增加到10-6g0时，表面张力作用仍较为明显。箱体内部物理场分布与0 g0工况大致相同。当重力水平增加到10-5g0时，此时微重力影响与表面张力作用相当。具体表现为，在表面张力驱使下，液相已不能完全包裹气相，并且气相一直与箱体顶部接触，没有脱离壁面。当重力水平增加到10-4g0时，箱体内部自然对流已十分明显，气相区大致呈带状，并且与箱体顶部壁面有较大的接触面积。当时间较短时，箱体壁面漏热可通过自然对流及时带入箱体内部。通过监测箱体内部气相压力得出：箱体压力随时间增长呈先降低后逐渐升高的趋势。重力越小，箱体压力也越小。另外，通过对比两不同边界设置发现，边界条件不仅影响气相运动状态，而且还直接影响壁面流体温度分布。

1 李章国，刘秋生，纪 岩，等. 航天器贮箱气液自由界面追踪数值模拟术[J]. 空间科学学报, 2008, 28(1): 69-73.

Li Zhangguo, Liu Qiusheng, Ji Yan, et al. Numerical simulation of liquid-vapor interface tracking in tank of spacecraft[J]. Chin. J. Space Sci., 2008, 28(1):69-73.

2 黄晓波. 表面张力驱动对流的实验研究[J]. 力学进展, 1989, 19(3): 353-364.

Huang Xiaobo. Experimental study of surface-tension driven convection[J]. Advances in Mechanics, 1989, 19(3): 353-364.

3 AydelottJ.Normal gravity self-pressurization of 9-inch(23cm) diameter spherical liquid hydrogen tankage[R].NASA TN D-4171,1967.

4 王赞社,顾兆林,冯诗愚,等. 低温推进剂贮箱增压过程的传热传质数学模拟[J]. 低温工程,2007,160(6):28-37.

Wang Zanshe, Gu Zhaolin, Feng Shiyu, et al. Simulation of heat transfer and mass transfer in cryogenic propellant tank pressurization process[J]. Cryogenics, 2007,160(6):28-30.

5 ZilliacG,ArifKarabeyoglu M. Modeling of propellant tank pressurization[R].AIAA2005-3549, 2005

6 Panzarella C,Kassemi M.Self-pressurization of large spherical cryogenic tanks inspace[J].Journal of Spacecraft and Rocket,2005,42(2):299-308.

7 Sim J, Kuan C K, Shyy W. Simulation of spacecraft fuel tank self-pressurization using Eulerian-Lagrangianmethod[R].AIAA 2011-1318.

8 Grayson G D,Lopez A, Chandler F O, et al. Cryogenic tank modelingfor theSaturnAS-203 experiment[R].AIAA 2006-5258.

9 Mattick S J, Lee C P, Hosangadi A, et al. Progress in modeling pressurization in propellant tanks[R].AIAA 2010-6560

10 刘 展, 厉彦忠, 王 磊,等.在轨运行低温液氢箱体蒸发量计算与增压过程研究[J]. 西安交通大学学报, 2015, 49(2): 135-140.

Liu Zhan, Li Yanzhong, Wang Lei, et al. Evaporation calculation and pressurization process of on-orbit cryogenic liquid hydrogen storage tank[J]. Journal of Xi'an Jiaotong University, 2015, 49(2): 135-140.

11 Ahuja V, Hosangadi, A Mattick S J, et al. Computational analyses of pressurization in cryogenic tanks[R]. AIAA,2008:4752.

12 闵桂荣. 卫星热控制技术[M].北京:中国宇航出版社, 1991.9.

Min Guirong.Satellite thermal control technology[M].Beijinh:China Astronautic Publishing House,1991.9.

13 Kartuzova O, Kassemi M. Modeling interfacial turbulent heat transfer during ventless pressurization of a large scale cryogenic storage tank in microgravity [R]. AIAA2011-6037.

14 Wang L, Li Y, Zhao Z, et al.Transient thermal and pressurization performance of LO2tank during helium pressurization combined with outside aerodynamic heating[J]. International Journal of Heat & Mass Transfer, 2013, 62(1):263-271.

Research on thermal stratification of cryogenic liquid oxygen tank in microgravity

Liu Zhan1Sun Peijie2Li Peng2Li Yanzhong1Jin Yonghua1

(1School of Energy and Power Engineering, Xi’an Jiaotong University, Xi’an 710049, China) (2Shanghai Institute of Aerospace System Engineering, Shanghai 201108, China)

One numerical calculation model is built to investigate the temperature distribution of on-orbit cryogenic oxygen tank in microgravity, with phase change and different space radiations considered. The results show that when gravity sets as 0 g0, the liquid would encircle the ullage under the influence of surface tension, and the spherical ullage breaks away from tank wall and moves toward the tank bottom. Local overheating appears in fluid close to tank wall due to the lack of free convection in tank. While gravity increases to 10-6g0, the effect of surface tension is still obvious and the tank physical distribution is almost the same as that of 0 g0. When gravity increases to 10-5g0, the liquid could not encircle the ullage fully and the ullage always touches the top of the tank. While gravity increases to 10-4g0, free convection becomes more and more evident. The ullage looks like a ribbon and touches a large area of tank top. The external heat leakage could enter the tank in short time by fluid free convection. Moreover, tank pressure reduces firstly and then increases gradually. A smaller gravity causes to a smaller tank pressure. Finally, it is found that initial boundary condition setup has a large influence on tank physical distribution.

microgravity;cryogenic liquid oxygen tank;thermal stratification;space radiation

2015-11-22；

2016-02-19

国家自然科学基金(51376142),航天低温推进剂技术国家重点实验室开放课题(SKLTSCP1407),上海航天核攀项目(ZY2015-015)项目资助。

刘 展，男，24岁，博士研究生。

TB657

A

1000-6516(2016)01-0025-07