基于控制线的开式整体叶盘环形刀四轴加工算法研究*

田荣鑫，邓 霜，张晓峰，任军学，姚倡锋，常威威

（1.西北工业大学现代设计与集成制造技术教育部重点实验室，西安 710072；2.中国航天科技集团公司六院7103厂，西安 710100）

航空发动机是飞机的核心部件，直接影响飞机的可靠性，它是一个国家科技、工业、国防实力的重要体现。开式整体叶盘是现代高推重比航空发动机采用的新结构[1]（图1），开式整体叶盘解决了传统叶片与轮盘装配结构所表现的连接部分易疲劳、寿命低、装配误差不可避免的缺点，同时整体叶盘的叶片与轮盘作为整体结构加工出来，大大减小了叶盘的结构重量和零件数量，极大地简化了发动机结构；另一方面，整体叶盘采用的宽弦、弯掠叶片和窄流道结构有效地提高了气动效率[1]。随着轻质、高强度、耐高温材料（如钛合金、高温合金和复合材料等）广泛地应用于整体叶盘的制造中，其可靠性和工作性能得到了进一步的提高。

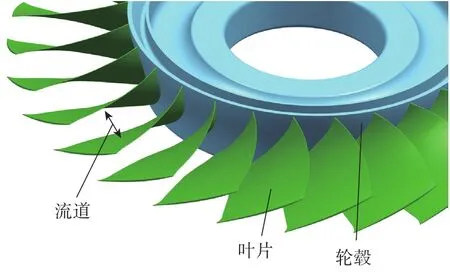
图1 开式整体叶盘结构示意图Fig.1 Structure diagram of open blisk

由于整体叶盘的结构特点，通道两侧的叶片多为复杂薄壁自由曲面结构，其几何精度要求较高，加工叶片还要受到内轮毂与相邻叶片的约束，通道内腔槽复杂、开敞性差，容易发生干涉，因而刀轴方向难以控制。此外整体叶盘的叶片具有薄壁、刚性差、易变形、切除量大等工艺特性[2-3]，对刀具性能要求比较高，这给整体叶盘加工带来很大的困难。

针对整体叶盘的刀轴优化和刀具选择难题，国内外学者进行了大量的研究。Ho等[4]研究了利用典型位置来定义符合机床运动学特性的刀轴，采用四元数值差值计算中间位置刀轴矢量，并对其进行刀具干涉检验得出最后优化的刀轴矢量。Wang和Tang[5]通过计算每一切触点的有效角速度求得五轴加工中无干涉可用刀轴。Castagnetti等[6]提出在规划刀轴同时计算几何约束和机床运动学约束的方向可行域概念来优化刀轴。南京航空航天大学的姬俊峰等[7]借鉴动画设置关键帧的思想提出一种全局光顺刀轴矢量生成方式，能避免刀轴矢量突变引起的机床振动，但该算法程序依赖于曲面矢量，计算量大，算法冗余。西北工业大学的王晶等[8]提出一种基于临界约束的刀轴优化算法，获得的刀轴可以显著地改善机床运动的连续性，并避免刀具的干涉，但算法中采用点搜索法计算每一切触点的刀轴可行域来优化刀轴，工程应用中计算量大。西北工业大学的任军学等[9]提出了控制线控制球头刀刀轴加工整体开式叶盘的通道，该方法不仅可以解决开式叶盘叶片加工中的刀具干涉问题，而且有效地避免了刀轴突变引起的啃伤现象，明显提高了叶盘表面的加工质量，但算法基于球头刀刀心与待加工叶片等偏置面的特点，无法克服球头刀易磨损，加工中需要多次换刀的缺点。综合当前研究和实际加工现状，五轴加工的成本比较高，对机床刚性和刀具的要求都比较高，而基于控制线的球头刀四轴加工虽然解决了刀轴突变引起的啃伤现象，但是球头刀易磨损，加工中存在需要多次换刀的问题。

本文在利用基于控制线球头刀加工整体叶盘的理论基础上，结合环形刀切削线速度大，加工效率高，相同材料切除量下刀具寿命相对于球头刀更高[10]的优点，提出一种利用球头刀刀轴控制线解决环形刀刀轴控制进行四轴加工的算法。文章首先阐述基于球头刀四轴加工控制线的生成方法；其次在建立球头刀和环形刀的刀具与曲面啮合关系的基础上，确定球头刀和环形刀的刀轴关系并计算环形刀的刀位点，进而提出一种环形刀刀轴通过控制线的算法，并求出控制线的环形刀可用刀轴；最后对算法进行试验仿真及加工验证。

1 球头刀四轴加工刀轴控制线的生成方法

刀轴控制线是控制刀具在加工过程中刀轴变化的一条光滑样条曲线，在规划的刀位轨迹上，每一个刀位点在刀轴控制线上有相对应的刀轴控制点。每一个刀位点指向刀轴控制点的方向作为其刀位点的刀轴矢量方向，在加工中由刀位点和刀轴矢量共同决定刀具加工姿态。

在求取球头刀的四轴加工刀轴控制线时，首先将两侧的叶片型面以及内轮毂曲面向通道内侧偏置一个刀具半径加切削余量的距离，其中切削余量视情况而定，比如叶盘尺寸和加工工艺，叶盘尺寸越大余量越大，粗铣余量大于精铣余量等，得到通道内侧的偏置面，并在外轮毂处沿叶片边沿做半径为刀具半径的管道曲面，若没有管道曲面，则叶尖点与刀轴的距离可能小于刀具半径，从而发生干涉。

每个位于叶型偏置面上的刀位点，其可用刀轴区域均为一个扇形区域，如图2所示，该扇形区域的具体生成方法为：首先用一系列平行于刀轴方向的摆刀平面，面之间的间距由加工精度决定，来截取两个通道偏置面，得到两条叶型偏置面截面线；在这两条截面线上按一定的密度离散出一系列的刀位点，任取其中一个刀位点C，依次计算该刀位点与通道方向其余刀位点的矢量Vi1，并计算出C点在叶型曲面上的法矢N在摆刀平面上的分量N'，依次计算Vi1和N'的夹角ai，取夹角最小的矢量即为刀位点C在本截面线侧的临界刀轴矢量；过刀位点C，沿矢量N'方向做直线，和通道对侧的截面线相交于点C'，在C'和对侧的截面线上的开口之间按照一定的密度离散一系列的点，依次计算刀位点C和对侧一系列点之间的矢量vi2，以及这些矢量和矢量N'的βi，取夹角最大的矢量即为相邻叶片的临界刀轴矢量，如图中所示临界刀轴矢量分别为T1和T2；本截面线侧的临界刀轴矢量和相邻叶片的临界刀轴矢量之间的开口区域即为该刀位点的四轴无干涉刀轴摆动区间。

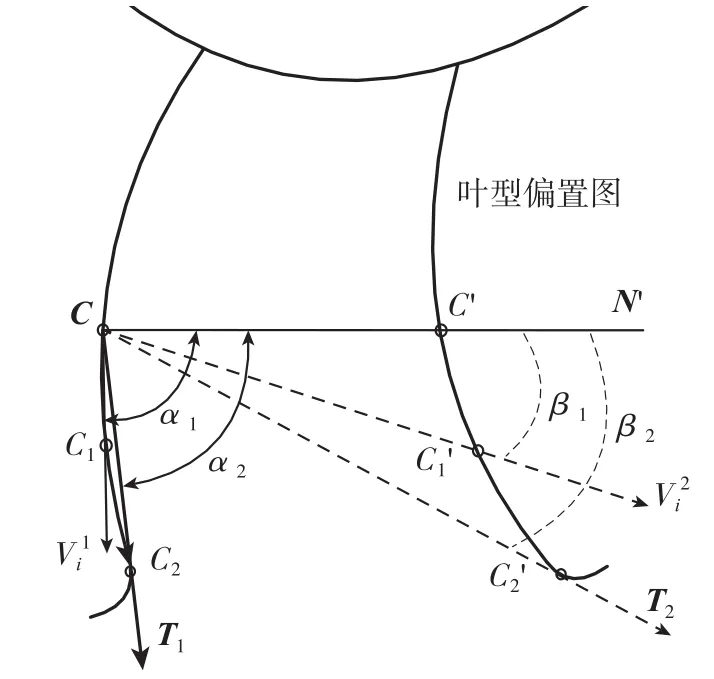
图2 无干涉刀轴求解Fig.2 Solution to the Interference-free Cutter Shaft

以叶盘回转中心为中心轴，考虑到刀具和刀柄对叶片的避让，利用大于叶盘半径的距离为半径构造一个回转圆柱面，则任意一个刀位点的无干涉摆动扇形区域与上述回转圆柱面交于一段圆弧线，该圆弧线即为无干涉刀轴摆动弧。如图3所示，求出叶盆侧摆刀平面内第i个刀位点的叶盆侧的临界刀轴矢量如图中实线所示，以及相对叶背侧的临界刀轴矢量如图中虚线所示，这两个刀轴矢量与回转圆柱面交于两个点，取叶盆侧所有刀位点对应的两个交点中距离最近的两个点CT1和CT2，过这两个点，以摆刀平面和叶盘中心轴的交点为圆心，得到的圆弧即为该摆刀平面内所有刀位点对应的无干涉摆刀曲线。理论上，该无干涉摆刀曲线上任意一点和任一刀位点的连线所得的刀轴都是不干涉的。用上述方法求取所有摆刀平面内的无干涉摆刀曲线，并将这些曲线组拟合成一个曲面，即为叶盆侧的无干涉刀轴控制面，且无干涉刀轴控制面内的任意一点都可以作为四轴加工的不干涉刀轴控制点。叶背侧无干涉刀轴控制面求解同理。

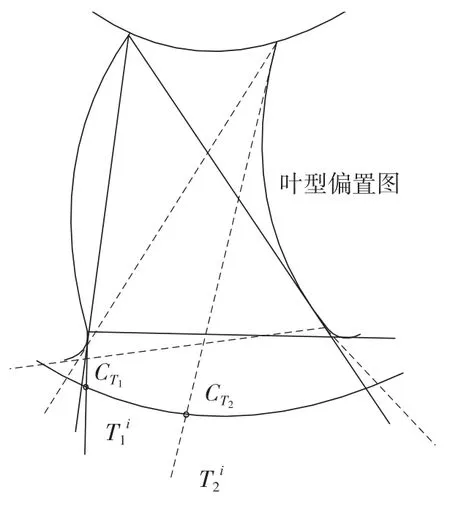
图3 无干涉刀轴摆动弧的求解Fig.3 Solution to the oscillating arc of the interference-free cutter shaft

为了获得较好的加工质量和加工效率，按照一定的生成准则[9]，沿着切削方向在无干涉刀轴控制面上生成一条曲线作为无干涉刀轴控制线。得到的无干涉刀轴控制线在加工中可以保证刀轴变化不依赖于曲面，刀轴变化较为平缓，从而使加工表面较为光顺。

但根据环形刀的刀具结构以及加工中切触关系，环形刀心点与切触点之间的距离随着曲面曲率的变化而改变，因而，环形刀刀心轨迹不在与加工平面等距离的偏置面上，因此环形刀控制线的生成方法中刀心点等偏置面不适应于环形刀刀心点轨迹，为了简化环形刀刀轴控制线的求解，可以采用球头刀的控制线，需要建立环形刀与球头刀的刀具与曲面啮合关系，确定刀轴之间的关系，并计算环形刀的刀心点。

2 球头刀和环形刀的刀位计算

为了计算环形刀与球头刀的刀轴关系，在确保两者刀轴与切触点法矢夹角相同的情况下，需建立环形刀与球头刀的刀具与曲面的啮合关系，以此确定环形刀与球头刀的刀轴关系和计算环形刀的刀心点。

2.1 球头刀和环形刀刀轴矢量的关系

为求取环形刀和球头刀的刀轴中心线，考察半径为R的球头刀和曲面的啮合关系，如图4（a）所示，及刀具半径为R、底刃半径为r的环形刀和曲面的啮合关系，如图4（b）所示。

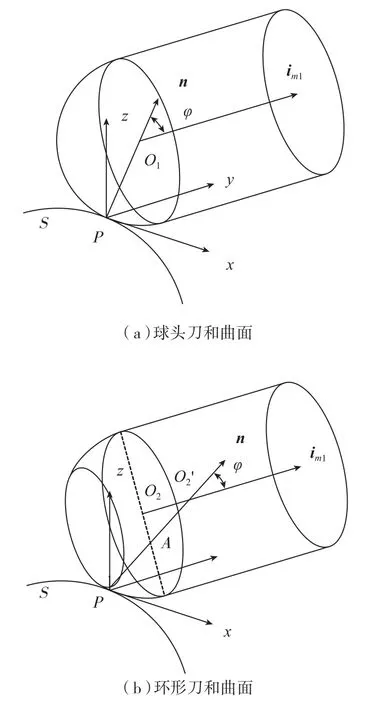
图4 刀具与曲面啮合关系Fig.4 Meshing relationship between the cutter and the curved surface

在图4（a）中，球头刀刀心O1位于法矢n上，和切触点P的距离为R，球头刀的刀轴矢量为im1，设im1与n的夹角为φ时，则球头刀的刀轴矢量集合为以O1为顶点的锥面P1（x，y，z）上，如图5（a）所示。在图4（b）中，环形刀切触点为P，环形刀底环环心与法矢n交点为A，刀心点为O2，刀轴与法矢n的交点为O2'，刀轴矢量为im2，当im2与n的夹角为φ时，则环形刀的刀轴矢量集合为以O2'为顶点的锥面上P1（x，y，z），如图5（b）所示。

在四轴加工模式下，当球头刀和环形刀与曲面切触于相同点P，且刀轴和法矢夹角φ也相同时，φ角度受到法矢n的约束。为完成四轴加工，刀轴矢量集合锥面必须与过锥面顶点的四轴摆刀平面有交线。

法矢n和摆刀平面有夹角α，不失一般性，令摆刀平面为XOY平面，设n=（i,j,k），则n与平面XOY的夹角有：

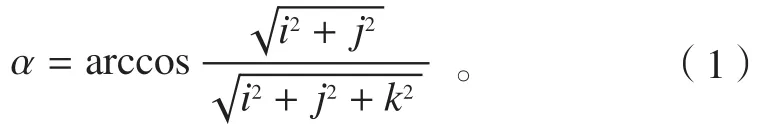
当φ＜α时，如图6（a）所示，刀轴集合与摆刀平面没有交线，不能完成四轴加工。

当φ=α时，如图6（b）所示，刀轴集合与摆刀平面只有一条交线，理论上能在四轴方式下实现刀具与加工面的啮合，但受开式整体叶盘复杂干涉结构的影响，无法完成整张曲面的连续加工。

当φ＞α时，如图6（c）所示，锥面P1与平面∑1有两条交线im1和i'm1，锥面P2与平面∑2有两条交线im2和i'm2，由于实际加工中开式整体叶盘通道的单向性，两条交线只能取指向通道外侧的一条做为可用刀轴。由图形的相似性可知im1//im2，i'm1//i'm2。

图5 空间刀轴集合模型Fig.5 Spatial model of the assembly of the cutter shafts

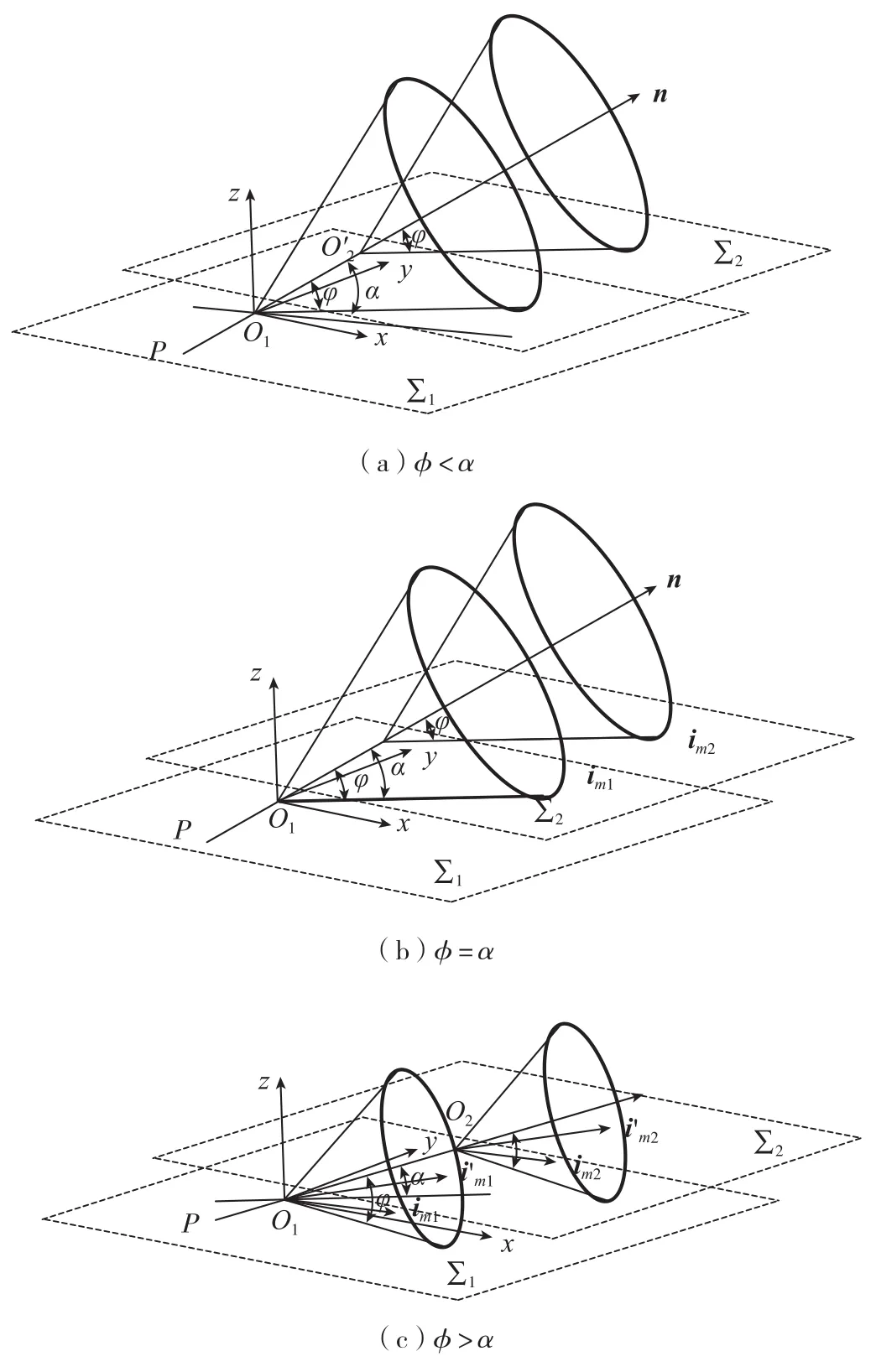
图6 可用刀轴空间关系Fig.6 Spatial relationships of the available cutter shafts

当球头刀和环形刀切触于曲面相同点P并进行四轴加工时，且刀轴矢量与曲面法矢n夹角同为φ时，环形刀的刀轴矢量和球头刀刀轴矢量平行。

2.2 环形刀刀位点的计算

图4（b）中所示，环形刀和曲面啮合于P点，前述已知刀轴矢量和曲面法矢夹角相同时，环形刀刀轴矢量和球头刀刀轴矢量平行。由球头刀刀轴矢量位于刀心点和刀轴控制线上等高点的连线上，可得环形刀刀轴矢量的方向，刀轴矢量标准化。考察刀轴矢量和曲面法矢n所构成的平面∑，图7所示。

A为环形刀底刃中心线与法矢n的交点，φ为刀轴与矢量n的夹角。在空间坐标系中，P点的坐标为（xp，yp，zp），法矢n为（i，j，k），im为（xm，ym，zm），得球头刀的刀心点O1的坐标：

式中，OP=（xp，yp，zp）。由几何关系可求得点 O'1的坐标：

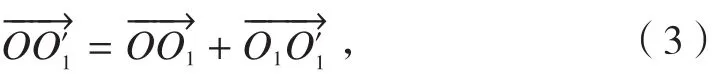
式中，，求取点A的坐标：，则矢量，同理可求得环形刀刀心点O2的坐标为：

式中，且：

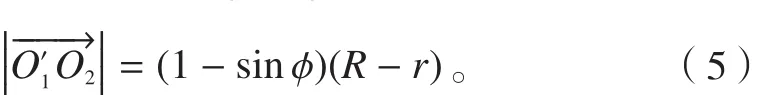
再根据环形刀端部内的几何关系，可知刀尖点T的坐标为：

式中，

得：

式中：im1和im2的空间距离就是环形刀采用四轴加工且刀轴矢量和切触点法矢夹角与球头刀相同时，环形刀和球头刀刀轴中心线之间的距离。球头刀刀轴中心线一定通过刀轴控制线，因此环形刀刀轴中心线和刀轴控制线有一定的距离，此时无法保障所生成的环形刀刀位轨迹不会产生干涉。为了避免环形刀加工中零件发生干涉，需要对环形刀刀位点和刀轴进行调整，通过改变环形刀刀轴矢量和切触点法矢夹角φ，使其通过球头刀的刀轴控制线，达到无干涉四轴加工的目的。

3 环形刀刀轴通过控制线方法

由于环形刀和球头刀在相同的φ角条件下，刀心点与切触点的距离不同，环形刀刀心线不通过球头刀控制线上的控制点，必须在环形刀四轴加工模式下调整φ角，使环形刀刀心线通过球头刀刀轴控制线。

如图7所示，环形刀和球头刀均与加工面切触于点P，当φ角发生变化时，球头刀为满足四轴加工，必须使im1在过点O1且平行于XOY，其理论摆动范围是360°，由于三角形是直角三角形，在此过程中O'1划过的轨迹均位于以AO1为直径的球面S1上，具体轨迹为平面Z=（zO1）与球面S1相交构成的圆O3,如图8所示。

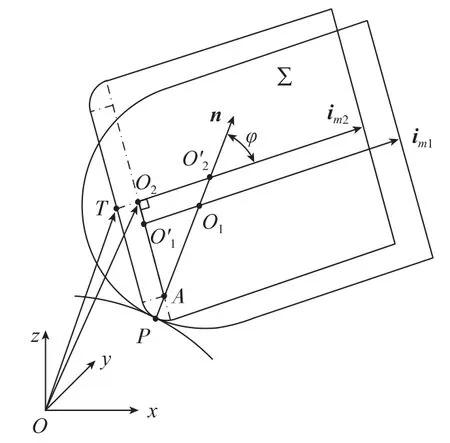
图7 基于控制线的环形刀刀位点计算Fig.7 Cutter location point calculation of the circular cutter based on the control curve

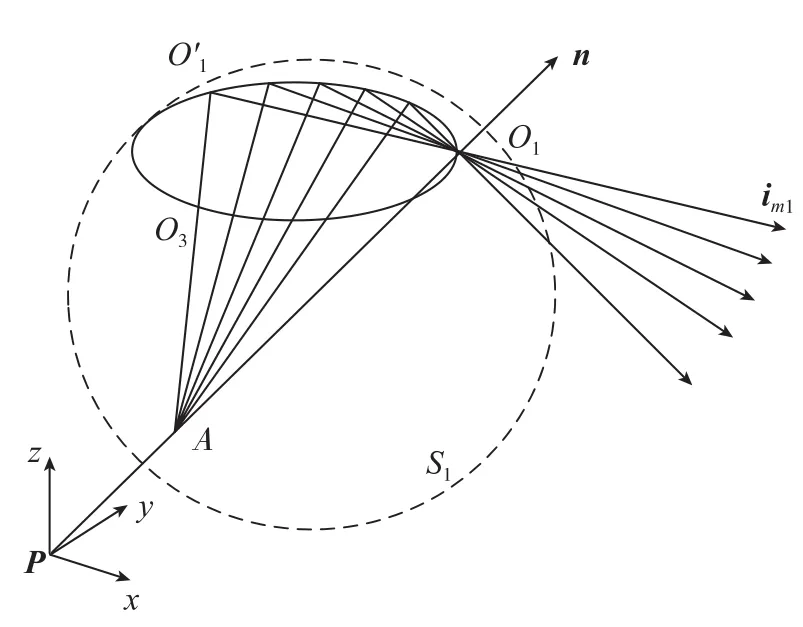
图8 球头刀刀尖点轨迹Fig.8 Tool nose point locus of the ball-end cutter

根据图7，|AO2|=R−r，可知环形刀刀心点一定位于以A为中心，以R-r为半径的球面S2上面，将延长，与球面S2的交点就是环形刀刀心点O2，随φ角变化，将圆O3沿点A投影到球面S2上，所得的曲线l就是所有满足四轴加工的环形刀刀心点集合，而每个刀心点所对应的刀轴矢量由曲线l和直线上等高点的连线确定，考虑到避免与叶片发生自干涉，其可用区域位于曲线和曲面法矢同侧的区域，如图9所示。

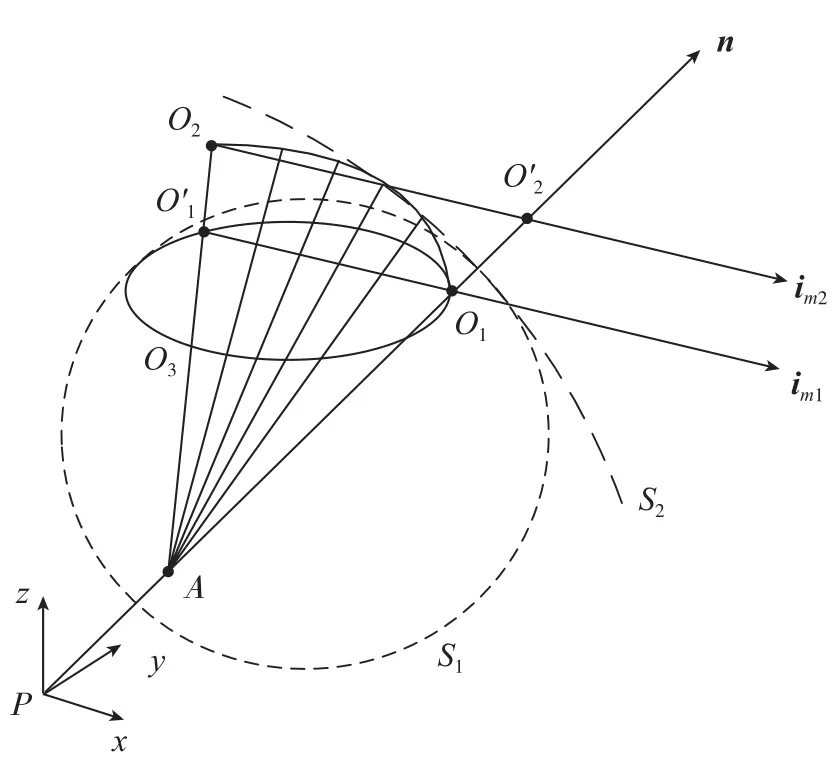
图9 环形刀刀心点轨迹Fig.9 Tool center point locus of the circular cutter

连接曲线l和直线上等高点构成直纹面∑'，并将其向流道外侧延拓至曲线l'，如图10所示，直纹面上的每条直纹线都是和加工曲面切触于P点的环形刀加工刀心线。图10所示的加工状态下，曲面法矢表明这是在加工一个向右上侧呈现凸出状态的曲面，即一个顺航向逆时针旋转的整体叶盘的叶背面，其球头刀控制线lk形状与叶背面趋势相同，向右上凸出的高度方向单调曲线，随高度升高，控制点从右下向左上变化。考察直纹面∑'，其环形刀刀轴中心线从O2O'2变化到极限状态O1O1"，由两个变化构成，第一个是与曲面法矢的夹角φ不断变大，第二个是刀轴中心线与曲面法矢的交点高度不断减小。刀轴中心线与曲面法矢的交点即等夹角刀轴矢量集合锥面的顶点，此顶点变化轨迹为从右上向左下变化；同时刀轴矢量集合锥面的顶角不断变大，使锥面与平面的交线不断单向远离锥面回转中心线，即环形刀刀轴中心线在叶盘通道外侧的延长线从右向左变化。这两个运动合成后对环形刀刀轴中心线直纹面∑'外侧边界线l'的影响是同位的，l'的变化规律是随着高度升高，从左下向右上单调变化。在极限状态下环形刀刀轴中心线O1O1"与曲面法矢垂直，φ=90°,在平面O1O1'O1"内，O1O1"位于球头刀刀轴控制点Kq的左侧，即位于刀轴控制线lk的左下侧；考察平行四边形O1O1'KqO2"内，O2O2"位于刀轴控制线右上侧，结合lk和∑'的单调性，可知lk与∑'必有且只有一个交点Kh，此交点就是环形刀四轴加工模式下通过球头刀刀轴控制线时的刀轴控制点，it就是环形刀通过刀轴控制线的刀轴矢量，点Ot是环形刀刀心点。

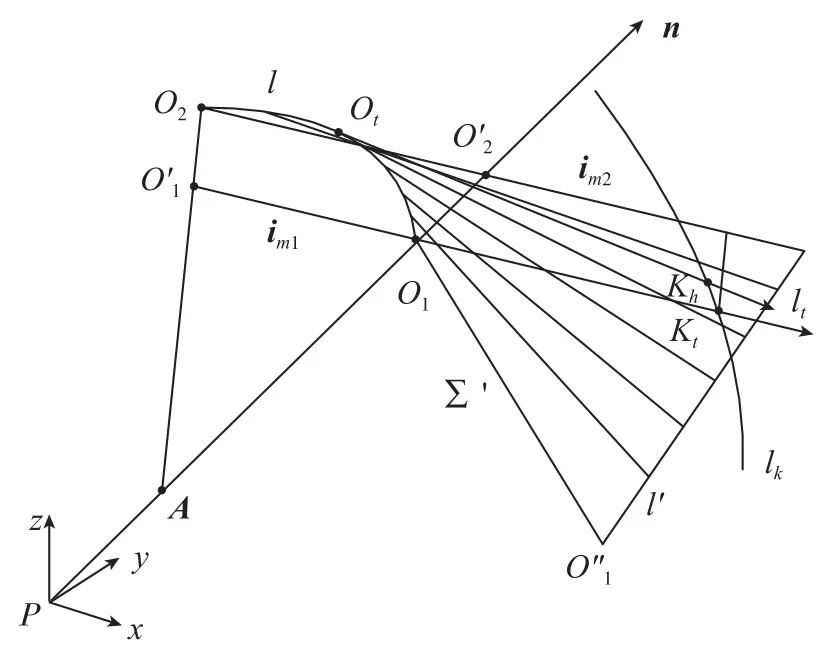
图10 过控制线环形刀刀轴计算Fig.10 Shaft calculation of the circular cutter over the control curve

采用环形刀通过球头刀刀轴中心线进行四轴加工，刀具中心点相比球头刀更加远离加工面，不会发生加工面自干涉。一般情况下刀轴控制线按照双侧干涉安全距离接近的方式构造，环形刀相比球头刀最大接近干涉面不大于，依公式（5），叶盘加工中φ均大于60°，按常用直径12mm底刃半径3mm的刀具估计，此时加工点附近的值为0.4mm，而干涉敏感区一般情况下位于叶尖处，且干涉安全距离一般大于0.5mm，将球头刀控制线用于环形刀刀轴控制一般不会出现环形刀他干涉，但加工前仍需对所编制的加工程序进行刀具及刀柄干涉检查。以上算例是一个顺航向逆时针旋转的整体叶盘叶背加工的情况，其他旋向及叶背、叶盆加工模式均可推导对应算法。

4 仿真分析及试验验证

基于前述算法构造的环形刀四轴加工开式整体叶盘的刀轴轨迹仿真，结果如图11所示。

图11 整体叶盘切削实验仿真图Fig.11 Simulation diagram of the blisk cutting experiment

利用本文提出的环形刀控制线方法进行加工试验，采用直径为12mm的环形刀，底刃倒角半径为3mm,齿数为4，切深为0.3mm，切宽为0.4mm，每齿进给量为0.025mm/r，主轴转速为5500r/min，进给速度为550mm/min。环形刀控制线方法加工试验现场如图12所示。

图12 加工现场图Fig.12 Map of machining spot

如图13所示为环形刀控制线加工后的叶片表面，可以发现叶片的刀痕整齐，纹理清晰，表面质量高。这是因为控制线控制下的刀轴不依赖于曲面形状，刀轴变化平缓，刀柄深入到叶盘通道内部使实际加工刀长变短，刀具振动小，加工表面质量非常好，表面粗糙度、叶身轮廓度指标均能满足设计要求。

5 结论

基于控制线的开式整体叶盘环形刀四轴加工方法，可以有效地解决加工过程中因刀轴变化率过大引起的叶片啃伤问题，提高了叶片加工表面质量，同时利用环形刀刀具磨损小解决了基于控制线球头刀四轴加工因为刀具易磨损需要频繁换刀的问题，提高了叶盘加工效率，在一定程度上降低了加工成本。

图13 加工结果局部图Fig.13 Local map of the machining result

采用环形刀带来的缺点是同样行距的情况下，残留高度相比球头刀加大。在某型整体叶盘加工中，曾采用的加工刀具从D8球头刀改成D12R3的环形刀，在同样是0.4mm行距的情况下，其残留高度从0.005mm增加到了0.0067mm，略微增大的残留高度仍是可以接受的，但实际工艺规划中仍需注意。若按等残留高度值进行加工，则环形刀相比同直径球头刀，其行距必须加密。

[1] 任军学,张定华,王增强 ,等,整体叶盘数控加工技术研究[J],航空学报,2004,25(2):205-208.

REN Junxue,ZHANG Dinghua,WANG Zengqiang,et al,Research on the CNC machining technique of blisk[J],Acta Aeronautica et Astronautica Sinica,2004,25(2):205-208.

[2] 任军学,姜振南,姚倡锋,等,开式整体叶盘四坐标高效开槽插铣工艺方法[J],航空学报,2008,29(6):1692-1698.

REN Junxue,JIANG Zhennan,YAO Changfeng,et al,Process for 4-axis high eff iciency slot plunge milling of open blisk[J],Acta Aeronautica et Astronautica Sinica,2008,29(6):1692-1698.

[3] 单晨伟,任军学,张定华,等.开式整体叶盘四坐标侧铣开槽粗加工轨迹规划[J].中国机械工程,2007,18(16):1917-1920.

SHAN Chenwei,REN Junxue,ZHANG Dinghua,et al,4-axis CNC sidemilling roughing path planning for open blisks[J],China Mechanical Engineering,2007,18(16):1917-1920.

[4] HO M C，WANG Y R，HU C H ,Five-axis tool orientation smoothing using quaternion interpolation algorithm[J],International Journal of Machine Tools and Manufacture,2003,43(12): 1259-1267.

[5] WANG N,TANG K,Automatic generation of gouge-free and angular-velocity-compliant five-axis tool path[J],Computer Aided Design,2007,39(10):841-852.

[6] CASTAGNETTI C,DUC E,RAY P,The domain of admissible orientation concept:a new method for five-axis tool path optimization[J].Computer-Aided Design,2008,40(9):938-950.

[7] 姬俊锋,周来水,安鲁陵,等,一类开式整体叶轮五坐标数控加工刀轴矢量生成及其光顺方法的研究[J],中国机械工程,2009,20(2):202-206.

JI Junfeng,ZHOU Laishui,AN Luling,et al,Generation and the smoothing method of 5-axis ncmachining tool orientation for the open integrated impeller[J],China Mechanical Engineering,2009,20(2):202-206.

[8] 王晶,张定华,罗明,等,复杂曲面零件五轴加工刀轴整体优化方法[J],航空学报,2013,34(6):1452-1462.

WANG Jing,ZHANG Dinghua,LUO Ming,et al,A global tool orientation optimization method for five-axis CNC machining of sculptured surfaces[J],Acta Aeronautica et Astronautica Sinica,2013,34(6):1452-1462.

[9] 任军学,杨大望,姚倡锋,等,基于控制线的开式整体叶盘叶片四轴数控加工刀轴控制方法[J],航空学报,2012,33(8):1515-1523 .

REN Junxue,YANG Dawang,YAO Changfeng,et al,A cutteraxis vector control method for open blisk 4-axis CNC machining based on the control curve[J],Acta Aeronautica et Astronautica Sinica,2012,33(8):1515-1523.

[10] 陈英,模具高速铣削刀具轨迹规划与工艺参数优选技术的研究[D].长春：吉林大学,2012.

CHEN Ying,Research on tool path planning and process parameter optimization technology of high speed milling for die[D],Changchun:Jilin University,2012.