基于模型重构的变形叶片配准定位技术*

蒋利洋，陈志同，江泽鹏，赵名绘，田茂璟

（1.北京航空航天大学机械工程及自动化学院，北京 100191；2.秦川机床工具集团股份公司，宝鸡 721009）

利用数字化检测手段对零件进行快速检测与重构，并进一步实现数字化检测——模型重构——数控加工一体化的集成加工，是提高航空发动机叶片类零件的制造精度、加工效率和自动化水平的关键技术，称之为叶片类零件自适应数控加工技术[1]。随着叶片精密制坯技术的快速发展，该技术成为了叶片类零件批量生产的主要加工方式之一，同时也是实现叶轮、叶片修复及再制造加工的重要方法。但是，前期工艺都只是相当于完成零件的粗加工过程，更为严格的加工精度、形状、位置要求需要最终的数控加工手段保证。无论是前期加工还是服役，都会使叶片产生变形和基准偏移，若利用叶片原始定位基准进行检测定位会造成余量不均甚至余量不足或超差的情况，同时影响曲面重构精度，带来加工误差。因此，如何保证变形叶片毛坯的精确定位是叶片数控加工的核心问题[2]。

本文所提到的配准定位就是对叶片毛坯进行在机测量，利用叶片的测量数据和它的理论数模进行配准对齐，实现调姿定位和余量均匀分配的目的。Arun等[3]提出的迭代最近点（ICP）算法在曲面配准领域得到广泛应用，但是，实际叶片毛坯型面测量点相较于理论模型发生了较大的变形，直接进行配准会产生较大误差。Sun等[4]建立了有余量约束的数学模型并对单张曲面配准问题进行了试验验证。张定华等[5]提出了考虑弯扭变形的叶片模型配准方法，首先通过测量设备获取叶片切片数据，建立弯扭变形曲线，据此对测量数据进行预变换，最后利用ICP算法进行配准，该方法对于成批具有相似变形规律的叶片具有一定的效果，但对于变形规律不一致的叶片而言难以实施。现有的配准定位算法[6-12]，如ICP算法、遗传算法、拟退火算法、能量算法等大多是针对余量较大的结构件的配准定位，对变形叶片的精准定位问题还不能很好地解决。

本文以叶片进排气边的自适应数控加工中的检测定位为研究对象，其特点为叶片进排气边未加工，叶身型面通过前期工艺已满足设计要求，但仍存在较大变形误差。据此提出了一种基于叶片特征参数的配准定位方法，通过在叶片原始基准坐标系下获取典型的测量点集进行求解分析，最终得到叶片变形量以及最优的坐标系变换。

1 模型重构与切片

对于点触式三坐标测量机，由于叶片毛坯面上的实测点存在法矢补偿误差，同时由于变形和粗定位偏差造成实测点与理论点并不一致，为此，本文采用直接采集测头球心点并进行曲面偏置的方式以获得准确的叶片偏差状态。另外，测量过程中设置测量机按照等Z值运动，尽量保证所采集的球心点处于同一平面，方便后续模型重构。

如图1所示，设球心采集点为Pij（i=1，…，m；j=1，…，n），m为测量截面线条数，n为每条截面线的测点个数。采用NURBS曲线和曲面原理对球心数据点Pij进行曲线和曲面拟合以得到叶片型面，该操作在三维建模软件中也较为容易实现，此处不再赘述。得到球心点拟合曲面之后，对其沿内法矢偏置测头半径以得到实际叶片毛坯曲面。

图1 曲面重构示意图Fig.1 Schematic diagram of curved surface reconstruction

获得偏置面（实际测量叶片毛坯面）之后，需要进行切片化处理，如图2所示。

具体操作为：利用若干等Z平面同时截取偏置面与理论模型，获得平面内的实测截面线与理论截面线，同时对实测截面线进行离散，以用于后续配准计算分析。

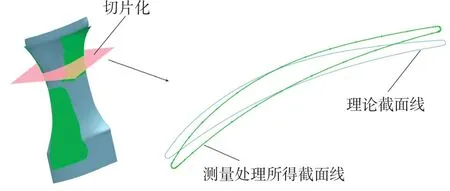
图2 叶片的切片化处理Fig.2 Slice processing of blade

2 配准定位模型的构建与求解

前期工艺下的叶片存在着较大变形，会直接影响配准求解结果，造成余量分布极不均匀。事实上，当叶片存在变形时，无论怎样求解都不可能得到余量均匀的情况。而如何在余量分布与变形量之间寻找较优的状态是本文研究的核心内容。

2.1 叶片变形定义

本文针对的是变形叶片，所以首先阐述叶片变形定义。叶片设计中，得到流面基元叶型之后，需要按照一定规律叠放以得到三维的叶片，即叶片积叠。叶片的积叠线可以位于叶片的不同位置，对于转子叶片，一般位于叶片流面的形心（积叠点），以减小叶片应力水平。如图3所示，X轴与Y轴交点为理论叶型积叠点，X'轴与Y'轴交点为实际叶型积叠点，其中轴与叶型相对位置不变，则叶片变形归纳为如下3种形式。

（1）扭变形：X轴与X'轴的夹角θ，也可以定义为弦线夹角（图3）；

（2）掠变形：理论积叠点到实际积叠点在X轴上的投影距离S（图4）；

图3 叶片扭变形Fig.3 Torsional deformation of blade

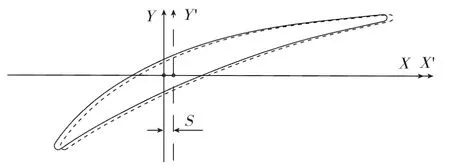
图4 叶片的掠变形Fig.4 Grazing deformation of blade

（3）弯变形：理论积叠点到实际积叠点在Z轴上的投影距离d（图5）。

图5 叶片的弯变形Fig.5 Bending deformationof blade

2.2 配准定位总体策略

基于模型重构的变形叶片配准定位方法总体分为以下5个步骤，流程如图6所示。

Step 1 粗配准：以叶片榫头（原始基准）作为粗定位基准，利用六点定位法或几何定位法进行粗定位；

Step 2截面线测量：提取叶片测量截面线，设置测量机按照定Z值运动，采集测量过程中的测头球心点坐标；

Step 3 模型重构：对每条截面线测量球心点分别进行拟合，并进行放样得到球心轨迹曲面，沿内法矢偏置测头半径得到实际叶片模型；

Step 4 切片：选取适当等Z平面对理论叶片模型和重构得到的实际叶片模型进行切片，每个平面内得到两组截面线，离散实际叶片模型上截面线获得若干点集。

Step 5 参数获取：将离散点集与对应的理论截面线进行配准，得到一个旋转两个平移参数，对每个等Z平面上的3个参数进行分析，得到最佳定位参数。

图6 配准定位总体流程图Fig.6 Generalflow-process diagram of registering and position

2.3 配准定位模型的构建与求解

（1）求取每条截面线点集的形心。离散得到的每条截面线点集为：

求解每条截面线上的数据点形心()以作为配准计算的原点。其求解按照如下公式进行：

（2）求取各个等Z截面数据的配准参数。

在等Z平面内的配准属于二维配准对齐，其可以调节的定位参数是在等Z平面内的平移量Δxi，Δyi绕Z轴的旋转量，其配准过程如图7所示。

图7 等Z面内的配准对齐Fig.7 Registering alignment of the equal Z values of the surface

（3）配准参数坐标系转换。

配准运算的坐标原点为叶片截面形心，而定位变换的坐标原点为叶片整体绝对坐标系，而绝对坐标系Z轴与截面的交点与截面形心并不重合，所以需要进行转换。

图8 配准参数的转换原理图Fig.8 Shifting principle diagramof registration parameters

如图8所示，设叶片截面形心为M，绝对坐标系Z轴与截面交点为N，MN与X轴夹角为φ。si、di、θi分别为叶片截面以N点为原点沿X轴的平移、沿Y轴的平移、绕Z轴的旋转。易知叶片截面绕M点顺时针旋转Δθi，等效于绕N点顺时针旋转Δθi与沿MN的垂线方向平移 2lsin（Δθ/2）。据此可求得si、di、θi，如下式所示：

则配准定位结果x=(Δα,Δβ,Δγ,Δx,Δy,Δz)T可按照以下4步求取：

Step 1: 如图9所示，拟合si-Z曲线，并求得最小二乘拟合直线l1，经分析，配准参数si反映的是叶片沿X轴的移动Δx和绕Y轴旋转Δβ的补偿量，l1与S轴的截距便是Δx，直线l1斜率的反正切便是Δβ。

图9 Δx与Δβ求解图Fig.9 Solving graph of Δx and Δβ

Step 2: 如图10所示，拟合θi-Z曲线，并求得最小二乘拟合直线l2，配准参数di反映的是叶片沿Y轴的移动 Δy和绕X轴旋转Δα的补偿量，l1与d轴的截距便是Δy，直线l2斜率的反正切便是Δα。

图10 Δy与Δα求解图Fig.10 Solving graph of Δy and Δα

Step 3: 如图11所示，拟合di-Z曲线，并最小二乘拟合得到直线l3（ 为了均化两端的最大偏差，此处的l2只能为平行于横坐标的直线且取拟合数据的中间值），则可得到Δγ。

图11 Δγ求解图Fig.11 Solving graph of Δγ

Step 4: 需要特别说明的是，经测量试验验证，以叶片榫头作为测量基准，叶片Z向配准定位的补偿量几乎为零，即Δz≈0,据此定位参数x=(Δα,Δβ,Δγ,Δx,Δy,Δz)T已全部得到，定位完成。

3 仿真验证

如图12所示，为某航空发动机理论叶片模型，在标准叶型上截取7个等距平面，对每个平面与叶型的交线（L1，…，L7）进行一定的旋转平移变换，利用曲面放样重构变换后的叶片模型，利用该叶片以仿真带变形实测叶片模型。将重构叶片模型按如下参数进行变换：(Δα,Δβ,Δγ,Δx,Δy,Δz)=（0,0,0,5,0.2,0.2,0），以仿真叶片基准偏差。

按照上文所述切片化方法处理得到截面点集如图12所示，将点集与截面曲线进行配准得到结果如表1所示。

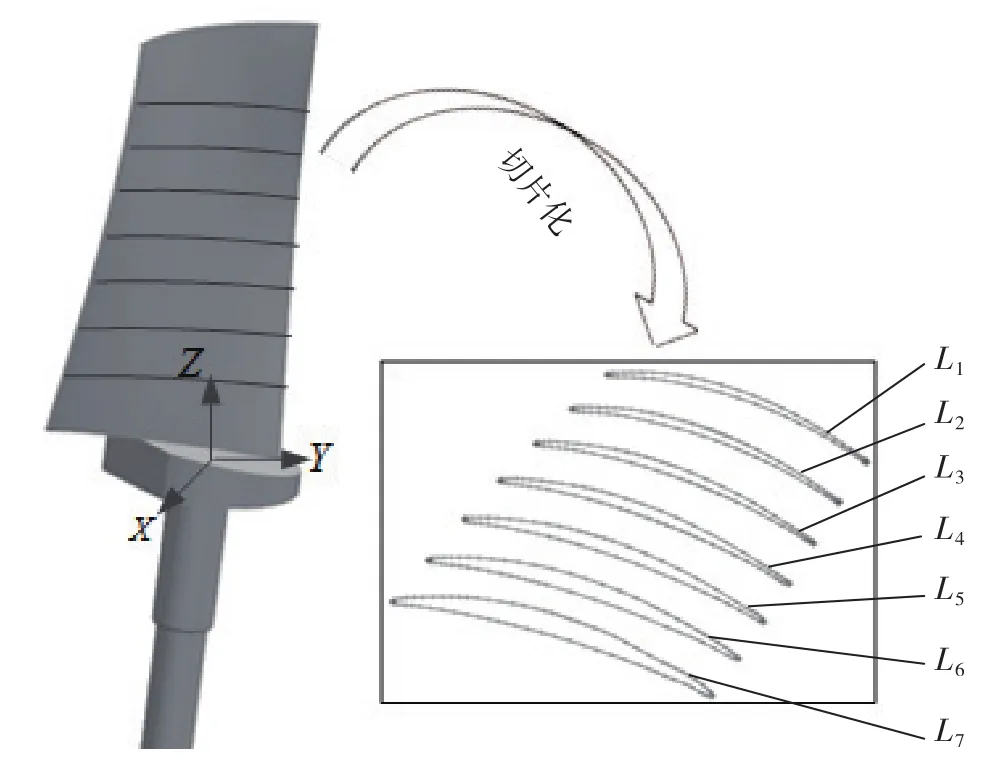
图12 航空发动机叶片模型Fig.12 Blade model of aero engine

获得每条截面线的旋转平移变换之后，以Z坐标为自变量，旋转平移变换为因变量进行线性拟合，最终结果如图13所示，其中，拟合函数为：

沿X轴平移函数：

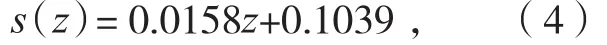
沿Y轴平移函数：

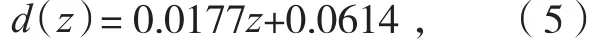
绕Z轴旋转函数：

表1 各截面配准参数

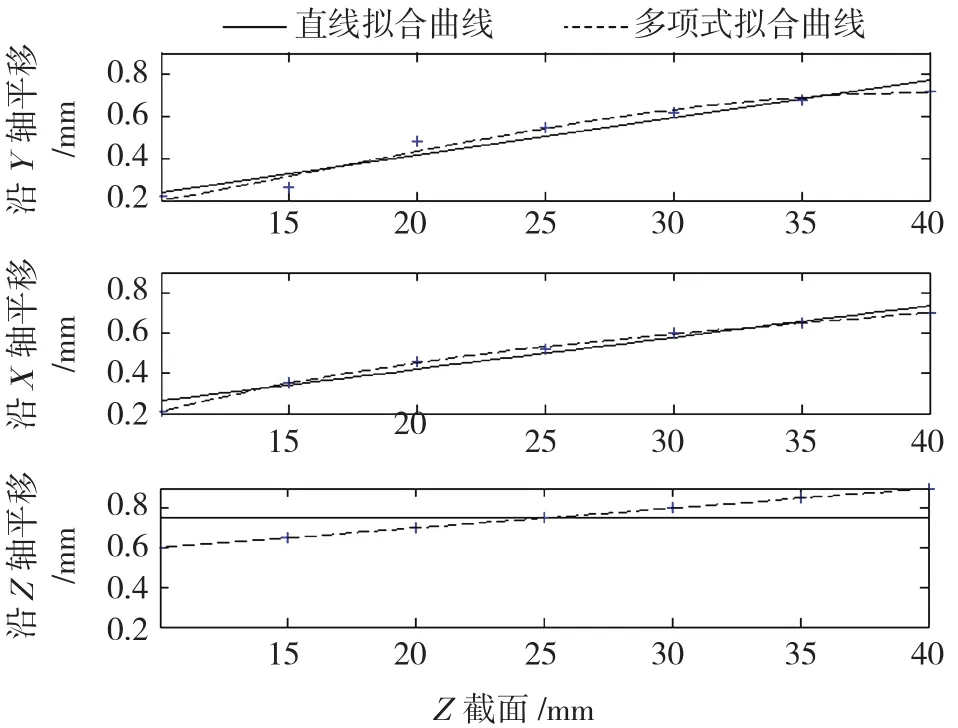
图13 拟合曲线Fig.13 Fitting curve

根据2.3节求取配准定位结果x=(Δα,Δβ,Δγ,Δx,Δy,Δz)T的分析和求解方法，式（4）所表示的直线方程的截距为Δx,直线方程斜率的反正切 为 Δβ，即，Δx=0.01039，Δβ=tan-1（0.0158）=0.900；同理 Δy=0.061，Δαtan-1（0.0177）=1.014；Δγ=0.750，故定位结果为（1.014,0.900,0.750,0.1039,0.061,0）。

不考虑叶片变形影响，利用ICP算法配准得到定位结果为（0.9256,1.1136,0.7510,0.0624,0.1105,0.03），对比结果如表2所示。

表2 配准数据对比

3种配准定位方式下，叶片加工余量分布（叶片偏差）如图14所示：原始理论偏差分布区间为[-0.61,0.999],榫头基准定位后的偏差分布区间为[-0.49,0.81],ICP配准定位后的偏差分布区间为[-0.256,0.446]，考虑叶片变形的配准定位偏差分布区间为[-0.165,0.192],按照本文提出的变形叶片定位方法配准定位后，其整体偏差小于无余量定位，偏差分布区间小，实现叶片余量整体均匀分布的目的。

图14 配准方法的对比分析Fig.14 Comparative analysis of registration method

4 结论

配准定位的目的在于使叶片整体余量尽可能小且均匀，但因为叶片在前期工艺下存在变形，所以几乎不可能实现叶片余量整体均匀的目的，因此，如何在叶片余量与变形间找到最优的折中状态，是本文研究的核心内容。从图14可以看出，利用榫头基准定位（即仿真设计中的变换参数）之后的偏差呈现明显的变形趋势，与仿真截面变换相符；采用无余量定位之后，最大偏差为0.446mm，按照本文的变形叶片定位方法配准定位后，其最大偏差为0.192mm，整体偏差较小且余量分布均匀，定位结果更加符合实际需求。因此，本文所述方法在变形叶片定位上效果显著。

[1] ZHANG D H,ZHANG Y WU B H,Research on the adaptive machining technology of blisk[J],Advanced Materials Research,2009,96-70:445-450

[2] 张莹,叶片类零件自适应数控加工关键技术研究[D].西安：西北工业大学，2010.

ZHANG Ying,Research on key technology of adaptive CNC machining of blade parts [D],Xi’an :Northwestern Polytechnical University,2010.

[3] ARUN K S,HUANG T S,BLOSTEIN S D,Least-squares fitting of two 3-D point sets[J],IEEE Transactions on Pattern Analysis and Machine Intelligence,1987,9(5):698-700.

[4] SUN Y,XU J,GUO D,et al,A unified localization approach for machining allowance optimization of complex curved surfaces[J],Precision Engineering,2009,33(4): 516-523.

[5] 张定华,程云勇,卜昆,等,考虑弯扭变形的叶片模型配准方法[J],航空学报,2009(12):2449-2455.

ZHANG Dinghua,CHENG Yunyong,BU Kun,et al,Reliable alignment method for blade shape analysis consideringits blend and twist deformation [J],Journal of Aviation,2009 (12): 2449-2455.

[6] 沈兵,高军,大型复杂曲面类毛坯最佳适配算法的研究[J].西安交通大学学报,1999,33(11):90-94.

SHEN Bing,GAO Jun,Best-fitting blanks of huge sculpture surface parts [J],Journal of Xi’an Jiaotong University,1999,33 (11): 90-94.

[7] 马骊溟,姜虹,贠敏,等,大型复杂曲面类毛坯加工定位的全局优化算法[J],系统仿真学报,2005(4):825-826.

MA Liming,JIANG Hong,YUN min,et al,A global optimization algorithm of localizationfor huge sculpture surface blank [J],Journal of System Simulation,2005(4):825-826.

[8] 李欢,基于实物测量的复杂毛坯加工余量优化分配技术研究[D],南京：南京航空航天大学,2013.

LI Huan,Research on optimal allocation of machiningallowance for complex blanks based on objects measurement [D],Nanjing：Nanjing University of Aeronautics & Astronautics,2013.

[9] 陈满意,李斌,段正澄,叶片零件毛坯余量分布优化问题研究[J],机械科学与技术,2006(2):246-248.

CHEN Manyi,LI Bin,DUAN Zhengcheng,Research on optimization of blank allowance distribution for bladeparts[J],Mechanical Science and Technology,2006 (2): 246-248.

[10] 曾艳,李斌,彭芳瑜,等,面向数控加工的大型螺旋桨桨叶的余量估算问题研究[J],中国机械工程,2006(6):566-569.

ZENG Yan,LI Bin,PENG Fangyu,et al,Research on the estimation of the propeller allowance in CNC machining[J],China Mechanical Engineering,2006 (6): 566-569.

[11] 孙杰,航空整体结构件数控加工变形校正理论和方法研究[D],杭州：浙江大学,2003.

SUN Jie,Study on correction theoryand method for distorted aeronautical monolithic component dueto CNC machining [D],Hangzhou:Zhejiang University,2003.

[12] 吴广宽,席光,粱武科,等,基于自适应遗传算法的叶片铸件最佳匹配问题求解[J],铸造技术,2006,27(2):101-104.

WU Guangkuan,XI Guang,LIANG Wuke,et al,Approach for blade roughcast optimal matching basedon self adapting genetic algorithm [J].Foundry Technology,2006,27 (2): 101-104.