机动期间的GEO卫星钟差确定方法

2016-06-01武美芳杨旭海

测绘通报 2016年4期

关键词：插值机动

武美芳，韦　沛，杨旭海

(1. 中国科学院国家授时中心，陕西西安 710600； 2. 中国科学院精密导航定位与定时技术重点实验室，陕西西安 710600； 3. 中国科学院大学，北京 100049)

机动期间的GEO卫星钟差确定方法

武美芳1,2,3，韦沛1,2,3，杨旭海1,2

(1. 中国科学院国家授时中心，陕西西安 710600； 2. 中国科学院精密导航定位与定时技术重点实验室，陕西西安 710600； 3. 中国科学院大学，北京 100049)

Method of Determination of GEO Satellite Precise Clock Bias during Maneuvering

WU Meifang，WEI Pei，YANG XuHai

摘要：分析了多种精密卫星钟差的插值方法，构建了GEO卫星机动模型，并结合插值方法，确定机动期间的GEO卫星钟差，并将结果与iGMAS最终产品进行了比较和分析。结果表明，三次样条插值是用于确定机动期间的GEO卫星钟差的最优方法,其结果精度可达0.01～0.38 ns。

关键词：GEO卫星；机动；精密卫星钟差；插值；卫星钟差确定

GNSS提供全球连续的定位与授时服务，目前最主要的应用包括导航测绘、国土资源监测、气象学、地震学、安全救援等领域。因此，精度并不是需要考虑的唯一参数，完备性、连续性、可用性、可靠性等也是值得关注的。我国自主建设和运行的北斗导航系统(以下简称BDS)，《北斗卫星导航系统公开服务性能规范(1.0版)》也明确规定了除精度之外的连续性、可用性的相关指标。

我国的BDS用地球静止轨道卫星(以下简称GEO)作为导航星座。但是，GEO导航卫星在轨道寿命期内，由于信号干扰、轨位限制等问题，必须定期进行机动，这种机动会产生推力，导致动力学建模误差，进而影响定轨精度和卫星钟差的确定。因此，在目前的BDS导航文件中，机动当天连续8 h，卫星状态为“不可用”，而在目前的精密钟差产品中，也不包含GEO卫星机动期间的钟差和轨道数据。这种情况一方面直接影响了BDS的可用性和连续性指标，制约了某些领域的应用，如安全救援和地震减灾；另一方面也给利用GEO卫星钟差产品开展的科学研究带来了一定的影响。因此，GEO机动期间卫星钟差研究及确定就显得极为重要。

卫星机动期间，只有星历、卫星钟差不可用，轨道等其他因素是完好的，如果能确定机动期间的卫星钟差，则卫星机动带来的影响可大大消除。从本质上来讲，机动期间的GEO卫星钟差确定是一个插值问题，即利用机动前后的已知的精密星钟差来内插得到机动期间的GEO卫星钟差。

一、钟差插值方法的分析

机动期间的GEO卫星钟差确定需要钟差内插，而用于内插的数学方法很多，如二次多项式插值、三次样条插值及高次多项式插值(如拉格朗日多项式、切比雪夫多项式)等，从理论上讲，这些方法都可以用于精密钟差的内插。

1. 二次多项式插值

卫星钟的钟差包括钟差、频偏、频漂及钟的随机误差。卫星钟的这种偏差可用二阶多项式的形式加以表示。设二阶多项式的系数分别为a0、a1、a2，由最小二乘求解模型参数，卫星钟差为卫星钟时间T与导航系统的时间t之差，其关系式如下

T-t=a0+a1(t-t0)+a2(t-t0)2

(1)

式中，t0为参考历元；系数a0、a1、a2分别为t0时刻的钟差、钟速及钟速的变率。因此，二阶多项式插值可用于卫星钟差插值。

2. 拉格朗日多项式插值

拉格朗日多项式插值模型也可用于钟差插值。但是，卫星钟差除了包括钟差、频偏、频漂等产生的误差外，还包含钟差的随机项，由于卫星钟差的随机项的不确定性，导致卫星钟差变化无规律可循，高次拉格朗日多项式用于钟差内插时的精度并不理想。国内的相关学者也证明了上述结论，并指出：当拉格朗日多项式的阶数取2时，可以得到最佳的内插结果，此时标准差和最大误差都最小；当阶数大于10时，内插精度越来越低，即多项式阶数越高，卫星钟差插值的精度越低，振荡现象越明显。因此，如果钟差的内插采用拉格朗日多项式，建议阶数不要超过10，以保证内插的精度和稳定度。

定义拉格朗日插值函数如下

(2)

式中

是n次插值基函数，满足条件

对于n阶插值，即有n+1个已知点，内插位于这n+1个点之间的任意位置的函数值。

3. 三次样条插值

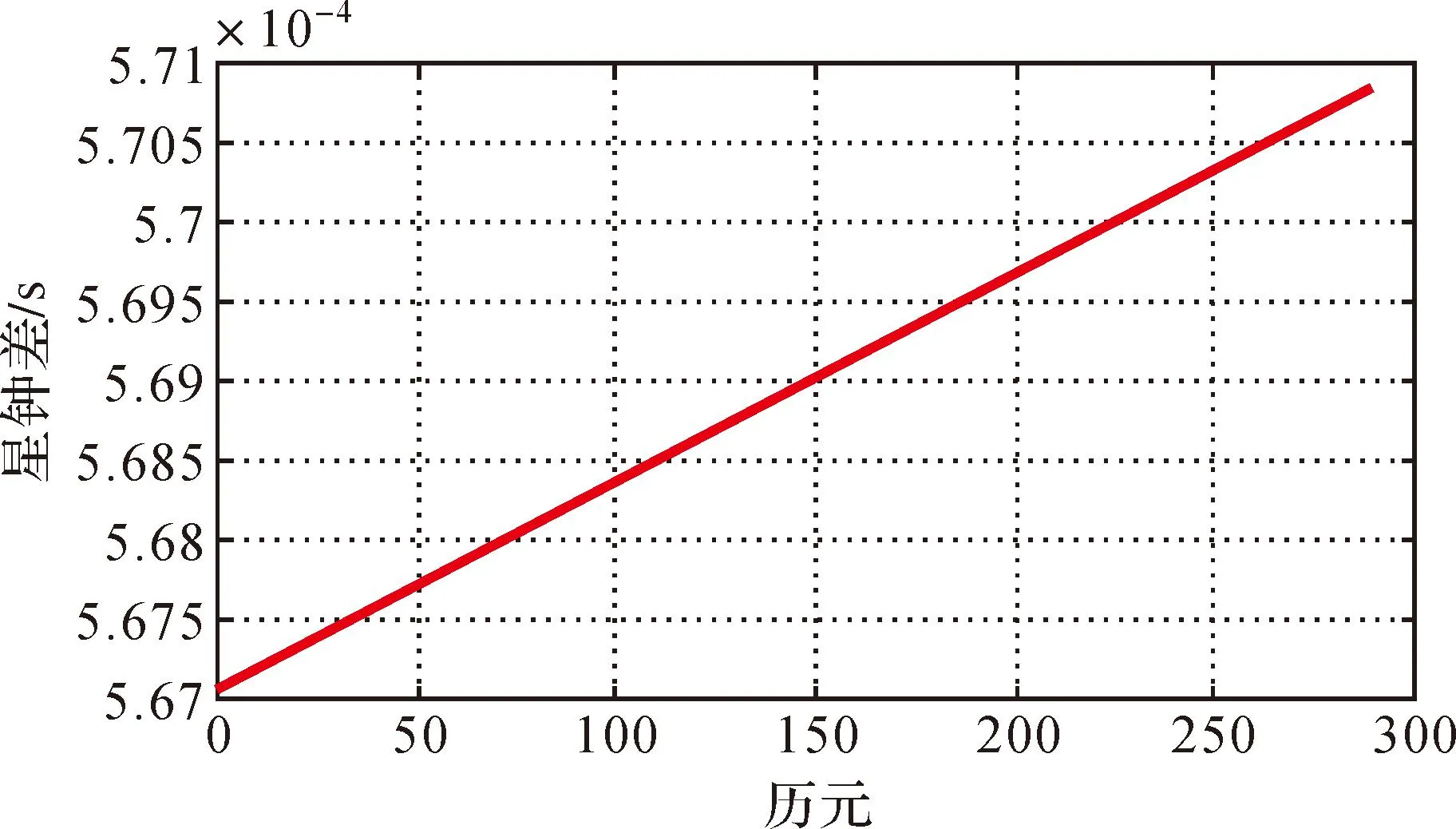
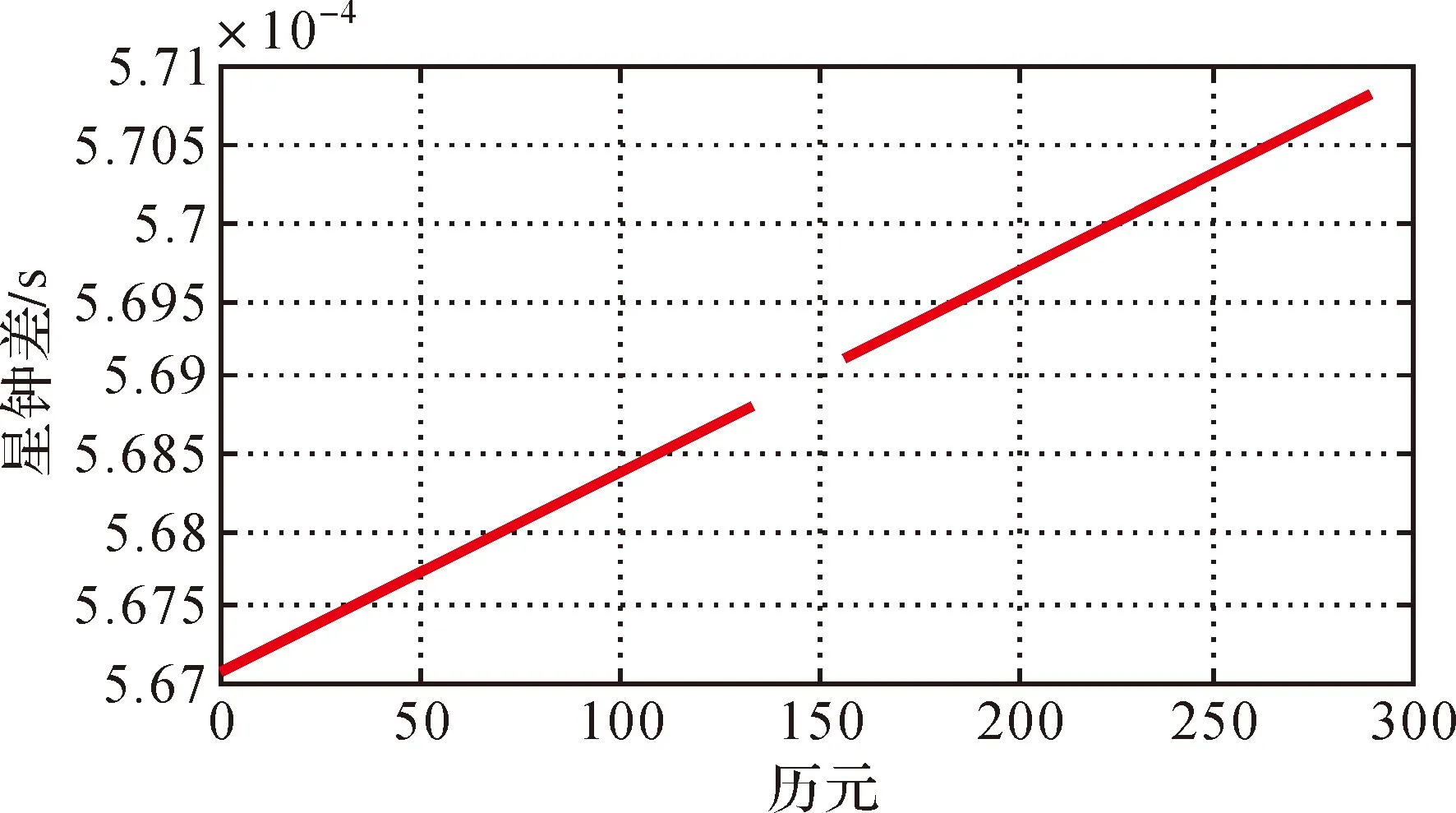
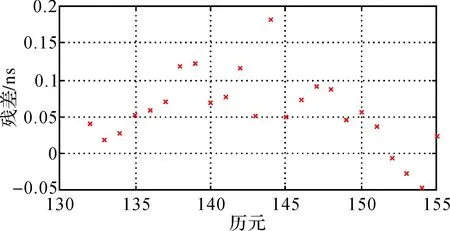
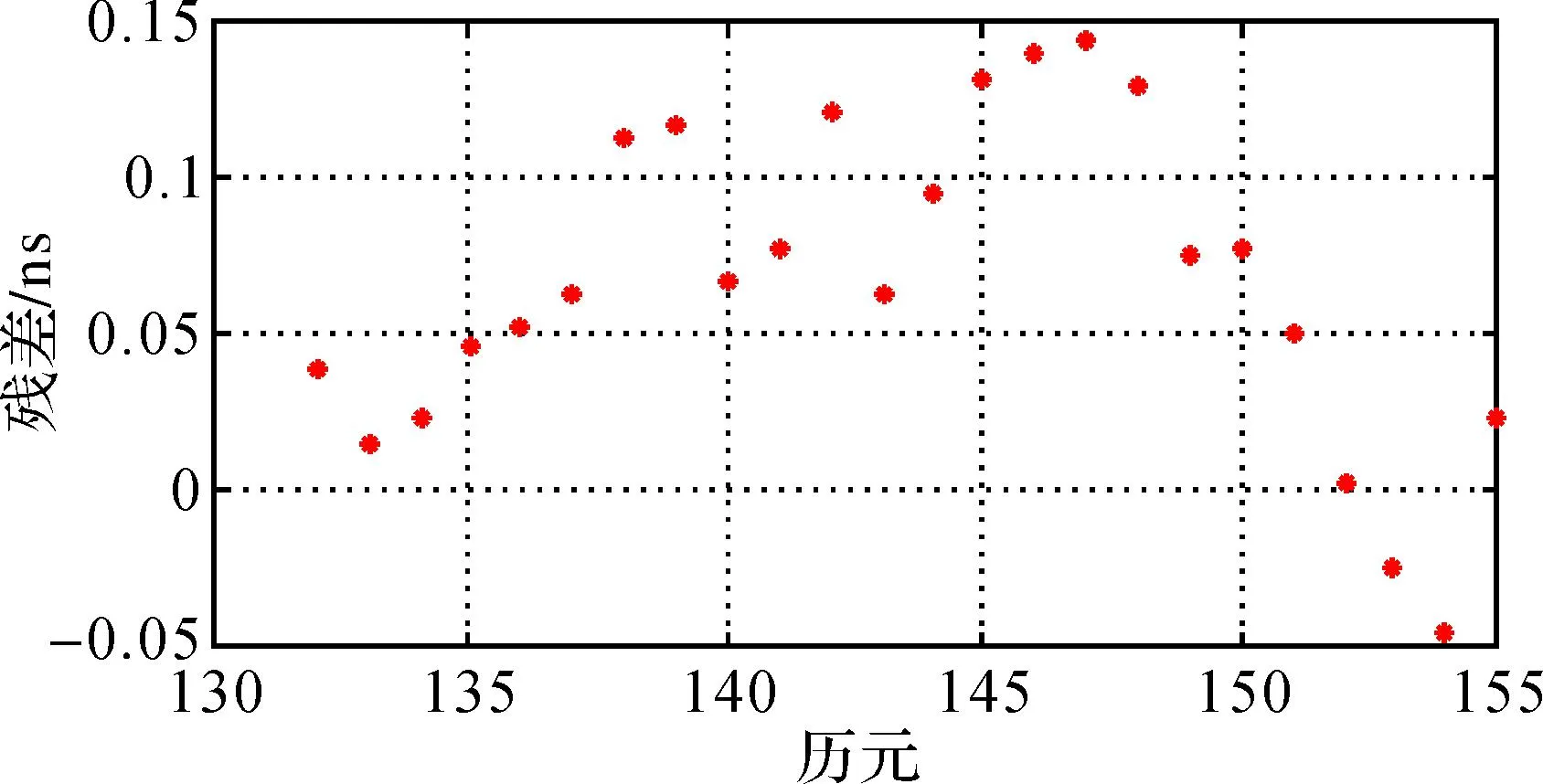
三次样条插函数是分段三次多项式，在每个节点处有2阶连续导数，设[a,b]上给出一组节点a≤x0

1)s(x)∈c2[a,b]。

2)s(x)在每个小区间[xi,xi+1](i=0,1,…,n-1)上是三次多项式，则称s(x)是节点x0,x1,…,xn上的三次样条函数。

3) 若s(x)在节点上还满足插值条件s(xi)=f(xi)，(i=0,1,…,n-1)，则称s(x)为[a,b]上的三次样条插值函数。

二、算例分析

1. 确定试验方案

本试验首先构造卫星机动期间钟差试验数据；其次利用插值模型对试验数据进行插值以确定GEO卫星机动期间的钟差，插值模型包括二次多项式、三次样条插值和拉格朗日多项式插值；最后，将iGMAS中GEO卫星精密钟差作为真值，用于检验3种模型的精度并得出结论。

2. 构造试验数据

GEO卫星机动当天，其广播星历中有连续8 h的数据状态显示为不可用，且没有事后精密钟差及轨道数据。因此必须利用GEO非机动时段的精密钟差数据构造GEO卫星机动数据作为试验数据。

非机动日的精密钟差数据为iGMAS官方网站上发布的BDS中2014年7月15日C03号GEO卫星的精密钟差数据，其采样间隔为5 min，一天共有288个历元，如图1所示。

图1　2014年7月13日C03号卫星精密钟差数据

由于在卫星机动当天，卫星的实际机动时间不会超过2 h，因此相应去掉非机动日精密钟差数据中连续2 h的数据，即图1中133—156个历元，生成GEO卫星机动数据作为试验数据。如图2所示，在生成的试验数据中，已知数据分为两部分，即第1—132个历元和第156—288个历元，长度264，有钟差数据；未知(待计算)数据为第133—156个历元，长度24，无钟差数据。

图2　生成的C03号卫星机动数据

3. 分析试验结果

使用生成的试验数据，结合拉格朗日多项式、三次样条和二次多项式3种插值方法，内插计算卫星机动期间缺失的钟差数据，并利用iGMAS提供的精密卫星钟差作为真值，计算插值残差，C03号卫星残差结果如图3—图5所示。

图3　C03号卫星拉格朗日插值计算残差

图4　C03号卫星三次样条插值计算残差

图5　C03号卫星二次多项式计算残差

由于目前iGMAS公布的BDS精密钟差的内符合精度在0.5 ns左右，因此，内插精度应该优于0.5 ns。为了验证该结论，分别计算3种模型插值残差的均方根误差和最大误差，并统计其插值精度，见表1。

表1　内插统计结果　ns

表1表示BDS 2014年7月15日C01—C05号，共5颗GEO卫星分别用3种插值模型得到的残差统计结果。从结果可以看出：

1) 二阶多项式模型在3种插值模型中，插值精度最差，最大时甚至大于1 ns，故不可用于确定机动期间的GEO卫星钟差。

2) 三次样条插值和低阶拉格朗日多项式的插值精度均在亚纳秒量级，均可满足实际应用需求。

3) 三次样条插值精度和低阶拉格朗日多项式的插值精度相差不大，约在0.01 ns量级。

4) 除C03号卫星外，三次样条插值的精度优于低阶拉格朗日多项式。

5) 三次样条插值的稳定性较好，其残差的最大值均小于其他两种插值模型。

6) 综上所述，确定机动期间的GEO卫星钟差，可以使用三次样条插值和低阶拉格朗日多项式插值方法。从优到劣为三次样条插值、低阶拉格朗日插值。

三、结束语

通过算例证明，大多数情况下，三次样条插值是3种方法中确定机动期间的GEO卫星钟差的插值方法中效果最好的插值方法。由于在iGMAS系统中，GEO卫星精密钟差精度在0.5 ns左右，而三次样条插值精度可达到0.01～0.38 ns(针对算例数据)，因此可认为三次样条插值结果能够满足实际应用的需求；同时，其插值的稳定性也明显优于低阶拉格朗日插值和二次多项式插值；并且，三次样条插值函数是分段三次多项式，在每个节点处有二阶连续导数，插值结果连续光滑，且插值计算简便，运算效率高。综上所述，三次样条插值是确定机动期间的GEO卫星钟差的理想方法。由此，机动期间的GEO卫星钟差可以通过三次样条插值得以确定，BDS的可用性、连续性指标得以提高，并且对利用GEO卫星钟差产品开展的科学研究具有一定的意义。

参考文献：

[1]KOUBA J.A Guide to Using International GPS Service(IGS) Products[R]. [S.l.]：IGS,2003.

[2]刘伟平，郝金明，于合理，等.导航卫星精密轨道与钟差确定方法研究及精度分析[J].测绘通报，2014(4): 5-7.

[3]雷雨，赵丹宁.三种综合预报卫星钟差的方法[J].测绘通报，2014(5): 22-25.

[4]刘冬，张清华.基于高斯过程的精密卫星钟差加密[J].测绘学报，2011，40(5)：59-62.

[5]洪樱，欧吉坤，彭碧波.GPS卫星精密星历和钟差三种内插方法的比较[J].武汉大学学报(信息科学版)，2006，31(6):516-518.

[6]叶聪云，罗涛，陈远，等.精密卫星钟差的内插方法研究[J].测绘信息与工程，2008，33(1):11-13.

[7]吴继忠，高俊强，李明峰.IGS精密星历和钟差插值方法的研究[J].工程勘察，2009(7):52-54.

[8]韩保民.精密卫星钟差加密方法及其对星载GPS低轨卫星定轨精度影响[J].武汉大学学报(信息科学版)，2006，31(12):1075-1078.

[9]郭东美，韩保民，熊熊.低轨卫星定轨中精密卫星钟差的插值方法[J].大地测量与地球动力学，2007，27(2):103-106.

[10]张丽，徐源强，李政.精密单点定位中卫星钟差插值方法研究[J].测绘通报，2013(7):16-18.

[11]何峰，王刚，刘利.地球静止轨道卫星广播星历参数拟合与试验分析[J].测绘学报，2011，40(5)：52-58.