一种有效的GNSS双差观测值组成方法

肖玉钢，刘鸿飞，陈渠森，袁　鹏

(1. 武汉大学测绘学院，湖北 武汉 430079； 2. 云南省测绘工程院，云南 昆明 650033；3. 武汉大学卫星导航定位技术研究中心，湖北 武汉 430079)



一种有效的GNSS双差观测值组成方法

肖玉钢1，刘鸿飞2，陈渠森1，袁鹏3

(1. 武汉大学测绘学院，湖北 武汉 430079； 2. 云南省测绘工程院，云南 昆明 650033；3. 武汉大学卫星导航定位技术研究中心，湖北 武汉 430079)

An Effective Double Differencing Method for GNSS Observations

XIAO Yugang，LIU Hongfei，CHEN Qusen，YUAN Peng

摘要：针对目前常用的GNSS双差观测值组成方法所存在的缺点，提出一种基于全局搜索的双差映射算法，并利用实测数据对各双差方法进行了比较分析。结果表明，基于全局搜索的双差映射算法适用于所有观测环境，且所得双差观测值个数与参考站-参考星法差别不大，是一种较为理想的双差映射方法，可以在科研生产中推广应用。

关键词：GNSS；双差观测值；全局搜索；参考站；参考星

GNSS相位观测值的双差解算可在保持原有精度的条件下，大幅减少待估参数个数，降低数据处理的工作量和复杂程度[1-3]。同时，双差解算还可消除或削弱观测方程中未模型化的系统误差，提高导航定位的精度与可靠性[4-8]。尤其在地球动力学研究、变形监测等对定位结果精度要求较高的领域，GNSS双差解算的优势更加明显[9]。

为进行双差解算，每历元的GNSS单程相位观测值均需经双差映射转化为双差观测值，进而采用滤波或法方程叠加的形式处理每历元观测，得到待估参数估值。双差映射的过程需满足两个条件：一是生成的双差观测值之间函数独立；二是尽可能多地形成双差观测值，以保证原始观测资料的充分利用[10-11]。GNSS双差观测值的组成方法有单差-双差法[12]、参考站-参考星法[13]等。单差-双差法将双差定义过程分为两步，从而使双差定义简单化，但某些时候不能定义出所有函数独立的双差观测值[14]。参考站-参考星法通过定义参考站或参考星完成双差映射，具有形式简单、算法实现方便等优点，且可搜寻出当前历元所有函数独立的双差观测值，是一种较为优秀的双差映射算法，但当某历元观测不存在任何参考站和参考星时，该方法失效。

针对当前常用GNSS双差观测值形成方法的缺点，本文发展了一种基于全局搜索的双差映射算法。在详细论述全局搜索方法的实施步骤之后，本文采用实测数据，从双差映射的可用性和有效性等角度出发，对新方法和传统方法进行了比较分析，所得结论对科学研究和生产实践均具有一定的实际意义。

一、一般双差组成方法

传统的双差组成方法有单差-双差法、参考站-参考星法等，其中以参考站-参考星法应用最为普遍。

1. 单差-双差法

单差-双差法首先在站间差分形成单差观测值，再利用单差观测值在卫星间差分，生成双差相位观测值。设某历元m个测站对n颗卫星观测，则原始单程相位观测值可表示为

φ=[φ11φ12…φ1nφ21φ22…φ2n

…φm1φm2…φmn]T

(1)

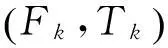
Δφ=Sφ

(2)

(3)

式中

(4)

星间单差在卫星间进行。对站间单差观测值再进行星间单差即得双差观测值

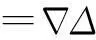
(5)

(6)

单差-双差法形成的双差观测值之间线性无关，且可用于所有观测历元。但由于在构成双差映射矩阵D的过程中首先需进行站间单差，若某站星之间不存在观测值则可导致形成的双差观测值组不是最大线性无关组，即丢失了部分线性无关的双差观测值。

2. 参考站-参考星法

为解决单差-双差法容易丢失线性无关双差观测值的问题，Bock等提出了参考站-参考星法[13]。某历元对所有卫星均有观测的测站称为参考站；对所有测站均有观测的卫星称为参考星。参考站法与参考星法类似，下面仅针对参考站的情况简要介绍该方法。

3. 基于全局搜索的双差组成方法

针对一般双差映射方法存在的缺点，本文提出了一种基于全局搜索的双差组成方法，下面简述其实施步骤。

设某历元3个测站对3颗卫星观测，其中第一个测站对第二颗卫星没有观测值，则此历元的原始单程相位观测向量为

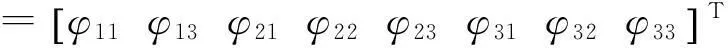
(7)

若基线按1-2、1-3定义，则根据单差-双差法组成的双差观测值向量为

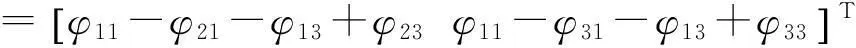
(8)

对同样的观测，利用参考站-参考星法形成的双差观测值向量为(以测站2为参考站)

Dφ=[φ11-φ21-φ13+φ23φ21-φ31-φ22+φ32

φ21-φ31-φ23+φ33]T

(9)

针对式(7)所示的实例，采用全局搜索法得到的双差观测值向量为

Dφ=[φ11-φ21-φ13+φ23φ11-φ31-φ13+φ33

φ22-φ32-φ23+φ33]T

(10)

比较式(8)—式(10)可知，采用单差-双差法进行双差观测值映射可能会丢失部分双差观测值，而参考站-参考星法很好地解决了此问题，且由式(9)可知参考站-参考星法所得双差观测值组是最大线性无关组。但参考站-参考星法受观测环境等的限制，若某历元不存在参考站和参考星，此方法失效。在式(7)所示实例中，全局搜索法得到的线性无关双差观测值个数与参考站-参考星法相同，且不受参考站和参考星是否存在等限制，适用于所有情况的双差观测值映射，是一种通用方法。当观测条件较为复杂时，全局搜索法同样可能丢失部分线性无关双差观测值，但其概率和数量均远小于单差-双差法。

二、数据分析

为研究全局搜索双差映射方法的可用性和有效性，本文设计了试验，利用实测数据从多个角度出发对各双差组成方法进行了比较分析。

试验采用的数据为中国北部某省部分CORS网点及其周边IGS站共40个点2013年8月9日(年积日221)全天的原始观测值。截止高度角10°，采样间隔30 s，共计2880历元。

表1为3种双差映射方法的可用性统计结果。由表1可知，在本文所采用的试验环境下，单差-双差法及全局搜索法在所有观测历元均适用，而参考站-参考星法在绝大部分观测历元同样适用，但有34个历元因不存在参考站和参考星导致方法失效，说明与其余两方法相比，参考站-参考星法的可用性略差。

表1　各双差映射方法可用性统计

图1为3种双差方法在各历元所得双差观测值的数量。表2为各双差方法在试验时段内所得双差观测值的总量及其之间的比例关系。由于参考站-参考星法在试验时段内的34个历元失效，因此对双差观测值数量的统计仅针对剩余的2846个历元进行。由图1可知，在3种双差方法均有效的观测历元上，参考站-参考星法和全局搜索法所得双差观测值数量差别不大，而单差-双差法所得观测值数量明显小于其余两方法。此结论在表2中也得到证实。由表2可知，全局搜索法所得双差观测值数量与参考站-参考星法差别很小，只有424个。与试验时段内约80万的观测值总量相比，此差别对解算结果的影响可忽略。但单差-双差法所得观测值数量只是参考站-参考星法的95%左右，差别较为明显。结合表1对各双差方法的可用性统计结果可知，全局搜索法既保证了在所有观测历元的可用性，同时又可获得较多的线性无关双差观测值，因此是一种较为理想的双差观测值映射方法。

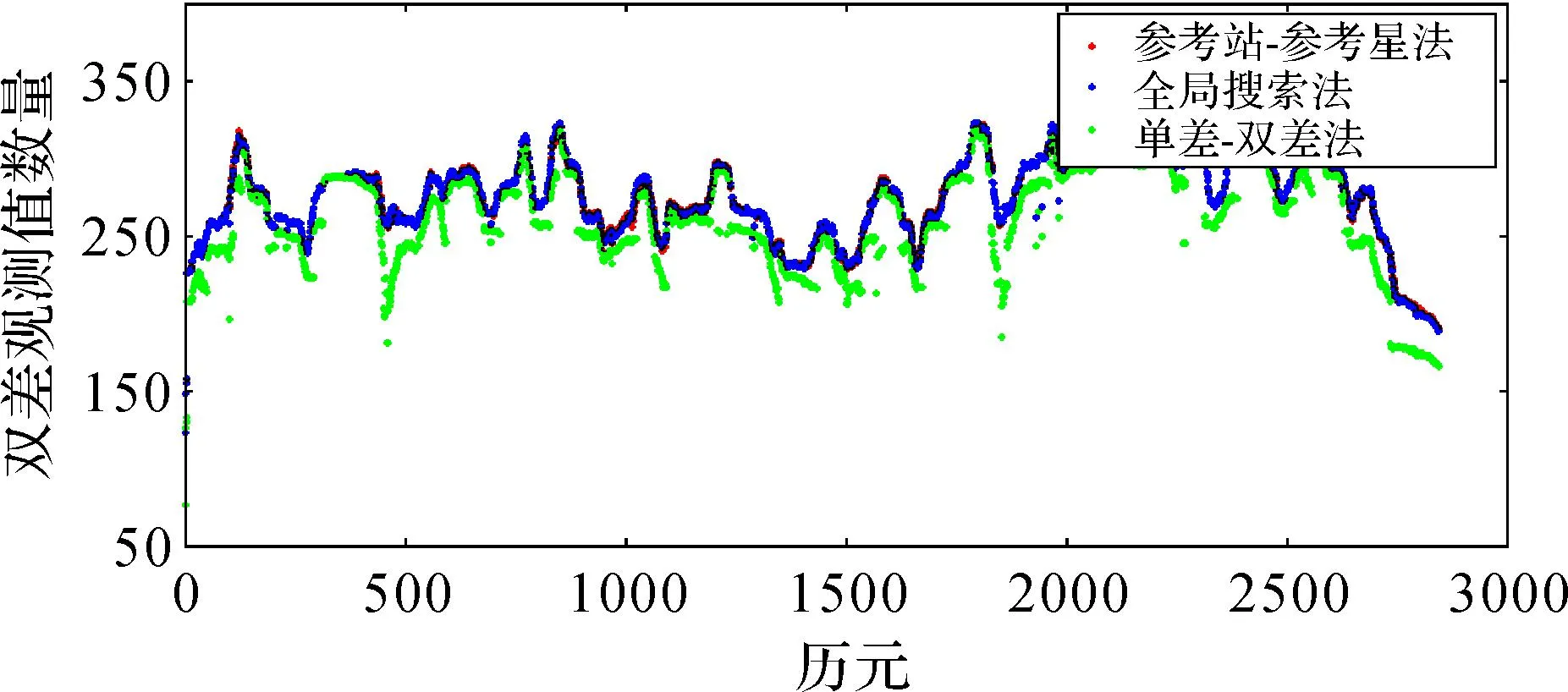
图1　不同双差方法在各历元所得双差观测值数量

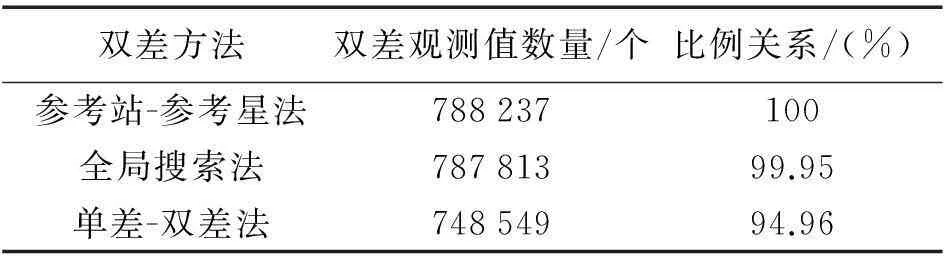
双差方法双差观测值数量/个比例关系/(%)参考站-参考星法788237100全局搜索法78781399.95单差-双差法74854994.96

注：比例关系以参考站-参考星法所得双差观测值数量为基准计算。

三、结束语

针对目前常用GNSS双差观测值组成方法所存在的缺点，本文提出了基于全局搜索的双差映射算法，并根据实测数据对其进行了分析。结果表明，全局搜索方法既可保证在所有观测历元的适用性，同时又可获得较多的线性无关双差观测值，因此是一种较为理想的双差观测值映射方法。

在实际的数据处理中，可根据每历元的观测情况选取不同的双差映射策略。若某历元观测存在参考站或参考星，则可采用参考站-参考星法；若某历元不存在任何参考站和参考星，则可采用全局搜索法，从而既最大限度地充分利用原始观测值，同时也保证了算法的稳定性和可靠性，有望得到更高精度的解算结果。

参考文献：

[1]DONG D N, BOCK Y. Global Positioning System Network Analysis with Phase Ambiguity Resolution Applied to Crustal Deformation Studies in California[J]. Journal of Geophysical Research, 1989,94(B4)：3949-3966.

[2]李征航, 黄劲松. GPS测量与数据处理[M]. 武汉：武汉大学出版社,2010.

[3]张双成, 曹海洋, 高涵, 等. 基于GAMIT的GPS短基线解类型分析及应用[J]. 测绘通报,2011(10)：27-29.

[4]BLEWITT G. Carrier Phase Ambiguity Resolution for the Global Positioning System Applied to Geodetic Baselines up to 2000 km[J]. Journal of Geophysical Research, 1989,94(B8)：10187-10203.

[5]BOCK Y. Establishment of Three-dimensional Geodetic Control by Interferometry with the Global Positioning System[J]. Journal of Geophysical Research, 1985,90(B9)：7689-7703.

[6]刘经南, 叶世榕. GPS非差相位精密单点定位技术探讨[J]. 武汉大学学报(信息科学版),2002,27(3)：234-240.

[7]赵姣姣, 曲江华, 袁洪. 针对北斗系统的降维快速高精度定向算法[J]. 测绘学报,2015,44(5)：488-494.

[8]任常, 白征东, 元荣. 变形量对双差模糊度固定的影响分析[J]. 测绘通报,2014(4)：30-32.

[9]李征航, 张小红. 卫星导航定位新技术及高精度数据处理方法[M]. 武汉：武汉大学出版社,2009.

[10]魏子卿, 葛茂荣. GPS相对定位的数学模型[M]. 北京：测绘出版社,1998.

[11]葛茂荣. GPS卫星精密定轨理论及软件研究[D]. 武汉：武汉测绘科技大学,1995.

[12]BEUTLER G, GURTNER W, BAUERSIMA I, et a1. Efficient Computation of the Inverse of the Covariance Matrix of Simultaneous GPS Carrier Phase Difference Observations[J]. Manuscripta Geodaetica,1986,11(4)：249-255.

[13]BOCK Y, GOUREVITCH S A, COUNSELMAN III C C, et al. Interferometric Analysis of GPS Phase Observations[J]. Manuscripta Geodaetica,1986(11)：282-288.

[14]刘经南, 葛茂荣. GPS相对定位中的双差新方法[J]. 测绘学报,1996,25(2)：110-115.

中图分类号：P228

文献标识码：B

文章编号：0494-0911(2016)04-0015-03

作者简介：肖玉钢(1984—)，男，博士生，研究方向为GNSS高精度定位定轨算法。E-mail: ygxiao@whu.edu.cn

基金项目：国家863计划(2012AA12A209)；国家自然科学基金(41374033)

收稿日期：2015-05-21；修回日期： 2015-12-01

引文格式： 肖玉钢，刘鸿飞，陈渠森，等. 一种有效的GNSS双差观测值组成方法[J].测绘通报，2016(4)：15-17.DOI:10.13474/j.cnki.11-2246.2016.0112.