GNSS精密卫星钟差估算与分析

万　军，党亚民，庞　辉，成英燕，王　虎，岳彩亚，3

(1. 中国测绘科学研究院，北京 100830； 2. 河北电力工程监理有限公司，河北 石家庄 050021； 3. 山东科技大学，山东 青岛 266510)



GNSS精密卫星钟差估算与分析

万军1，党亚民1，庞辉2，成英燕1，王虎1，岳彩亚1，3

(1. 中国测绘科学研究院，北京 100830； 2. 河北电力工程监理有限公司，河北 石家庄 050021； 3. 山东科技大学，山东 青岛 266510)

Estimation and Analysis of Multi-System Satellite Clock

WAN Jun,DANG Yamin,PANG Hui,CHENG Yingyan,WANG Hu,YUE Caiya

摘要：为估算与分析GNSS卫星钟差的精度，利用中国测绘科学研究院国际GNSS监测评估系统分析中心研发的软件，采用全球均匀分布的50个IGS跟踪站和8个我国自建的IGMAS测站的观测数据，对GNSS包含的四大导航系统事后精密卫星钟差进行了估计。计算结果分别与国际上的分析中心结果进行了比对，得出GPS卫星钟差与IGS结果互差在0.2 ns，GALILEO卫星钟差精度与GPS相当，在亚纳秒量级，GLONASS卫星钟差精度相对较低，在4 ns以内，BDS各轨道类型上卫星之间钟差存在较大的系统性偏差，选择多星基准消除偏差之后，估算的北斗卫星钟差精度在1 ns以内。试验结果表明，目前我国分析中心估算的卫星钟差总体上与国际IGS各分析中心估计的卫星钟差精度相当。

关键词：多系统；GNSS；卫星钟差；IGS；IGMAS

全球导航卫星系统(GNSS)包括美国的GPS、俄罗斯的GLONASS、欧盟的Galileo及我国的北斗导航系统[1]。随着GPS、GLONASS现代化进程的开展，以及Galileo计划与我国BDS的逐步应用实施，GPS已有32颗卫星提供导航定位服务；GLONASS在轨卫星也已达到29颗，其中有24颗卫星能提供正常服务；Galileo有4颗IOV卫星；我国共发射了16颗北斗导航卫星，其中14颗组网并提供服务，分别为5颗静止轨道卫星(GEO)、5颗倾斜地球同步轨道卫星(IGSO)，4颗中地球轨道卫星(MEO)。未来将是一个全球卫星导航系统的多系统融合时代，多系统组合定位能够增加可观测卫星数，优化卫星的几何图形结构，提高多系统组合定位精度和可靠性。多模GNSS数据融合与处理将是导航定位领域的主要发展趋势之一。

GNSS观测量是以卫星和接收机的钟频信号为基准获得的,卫星钟差与轨道一样，钟差精度的高低直接影响星地测距观测值的精度，进而影响导航、定位和授时服务的精度和稳定性[3]，特别是在非差精密单点定位中，高精度的卫星钟差尤为重要。国际上研究精密卫星钟差的机构主要是IGS服务组织及其各个分析中心，IGS在综合6家分析中心提供的GPS事后精密卫星钟差形成的最终产品，精度优于0.1 ns[4]；国内对卫星钟差估计的研究主要是针对单系统的，文献[5]利用预报卫星星历与若干个跟踪站伪距观测值一起估计GPS相对卫星钟差，相对精度为3～5 ns；文献[6]对GLONASS卫星的广播星历轨道及钟差进行了分析，其卫星钟差均方根误差在15 ns以内；文献[7]估计了Galileo在轨验证卫星的实时钟差，精度优于6 ns。

北斗导航系统2012年实现了具备覆盖亚太地区定位、导航和授时及短报文通信服务的能力，为全面拓展北斗国际化应用并为我国北斗卫星导航系统的观测数据和精密产品提供全球发布窗口，我国成立了相应的GNSS分析中心。本文利用中国测绘科学研究院国际GNSS监测评估系统分析中心研发的软件对北斗导航系统的卫星钟差进行了估计，并分析了目前我国GNSS分析中心提供其他系统精密卫星钟差产品的精度。

一、精密卫星钟差估算

在精密卫星钟差估算中,采用无电离层影响的非差相位和伪距观测值，观测值误差方程[1]为

(1)

(2)

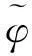
固定时间基准的措施包含以下几种方法：①引入基准钟，该基准钟钟差不变或线性变化，通常可固定某一个较稳定的测站钟，或将原子钟外接于观测站作为时间基准；②拟稳基准，引入一个钟群，认为该钟群钟差重心基准不变或呈某种已知的变化；③以广播星历卫星钟差改正项所隐含的时间基准为参考基准，目前广播星历的钟差已达到几个纳秒的精度，可满足要求。

为便于把估计结果和国际分析中心结果转换到同一时间基准下进行比较，本文算例采用引入基准钟的方法固定时间基准，GNSS观测值是测站与卫星之间的相对时间延迟，不能同时确定所有的卫星和接收机钟差，因此，先固定某一基准钟(卫星钟或接收机钟)的钟差，然后确定其他接收机和卫星的相对钟差[8]。只要保证基准钟的钟差精度优于10-6s,相对钟差和绝对钟差对用户定位结果而言是等价的，即相对钟差的系统性偏差在用户定位模型中可完全被用户接收机钟差吸收，而不影响用户的定位精度，本文所讨论的精密卫星钟差均指相对钟差。

二、试验分析

1. 试验方案

为研究我国GNSS分析中心提供的4个导航系统钟差产品的精度，特别是北斗卫星导航系统目前的卫星钟差精度及稳定性，基于分析中心研发的软件，对GNSS卫星事后精密钟差进行估算与分析。文献[3]选用了全球40个IGS测站一周的观测数据对GPS卫星事后精密钟差进行估计，精度与国际IGS分析中心相当。本文采用全球均匀分布的50个IGS跟踪站和8个我国自建的IGMAS测站(如图1所示)2014年12月11日—20日共10天的观测数据进行估算，为便于和国际上分析中心事后精密卫星钟差结果作比较，估算卫星钟差时采用5 min的时间间隔。

4个系统的卫星钟差解算结果分别与国际上较权威的分析中心提供的精密卫星钟差作比较并进行精度评定，其中把GPS卫星钟差与IGS结果、GLONASS卫星钟差与IGL结果、Galileo卫星钟差与TUM结果、北斗卫星钟差与GFZ结果进行比较。为避免因固定的基准钟不同导致时间基准不同，采用作二次差的方法，即先选择相同的一个参考卫星，分别将GNSS估算结果和国际上分析中心结果中其他卫星与参考星的钟差作一次差，消除了由于时间基准不同而对卫星钟差产生的影响，把消除了基准钟影响的估算结果与国际上分析中心结果作二次差，此时的结果可以有效反映出估算结果与国际上分析中心事后精密卫星钟差的符合程度。

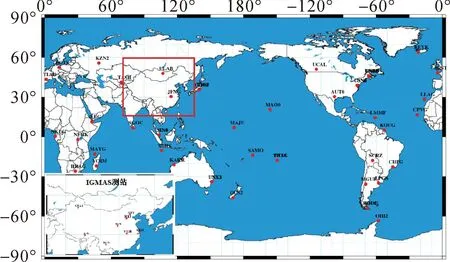
图1　50个IGS跟踪站和8个IGMAS测站分布

将每颗卫星10天所有历元的结果都作二次差，分别统计二次差时间序列的均方根σrms和标准偏差σsd，公式如下

(3)

(4)

式中，δi为每个历元的二次差值；δ为10天所有历元二次差值的均值；n为10天所有历元的个数；统计值σrms与σsd反映是否消除了系统性偏差的钟差精度的统计结果。

2. GPS/GLONASS/Galileo卫星钟差

GPS导航系统有32颗卫星提供导航定位服务，按照GPS在轨卫星钟类型分为铯钟与铷钟(见表1)。

表1　GPS卫星钟类型和卫星号对照表

分别选择GPS卫星01号星、10号星为参考星，图2(a)、(b)分别为以带有铷钟的01号星和带有铯钟的10号星为基准钟估算的GPS卫星钟差与IGS结果的二次差值。由图可以看出，带有铷钟的GPS卫星采用不同基准推算的σrms略有分别，但以01号星为基准钟估算的σrms整体的平均值比以10号星为基准钟估算的σrms整体的平均值小，带有铯钟的GPS卫星以10号星为参考星估算结果的σrms明显比以一号星为参考星估算结果的σrms小，说明铯钟与铷钟之间还存在一定的系统性偏差，且铯钟不如铷钟稳定；带有铷钟的GPS卫星两次估算结果的σsd明显都比带有铯钟的GPS卫星两次估算结果的σsd小，说明铷钟的精度比铯钟高。图2(c)为所有带有铷钟的卫星以01号星基准钟、带有铯钟的卫星以10号星为基准钟估算的GPS卫星钟差与IGS结果的二次差值。由图可以看出，GPS各卫星估算结果的σsd绝大多数都在0.2 ns以内，在消除卫星钟类型影响后的σrms与σsd仍有明显的差别，但也在0.6 ns以内。

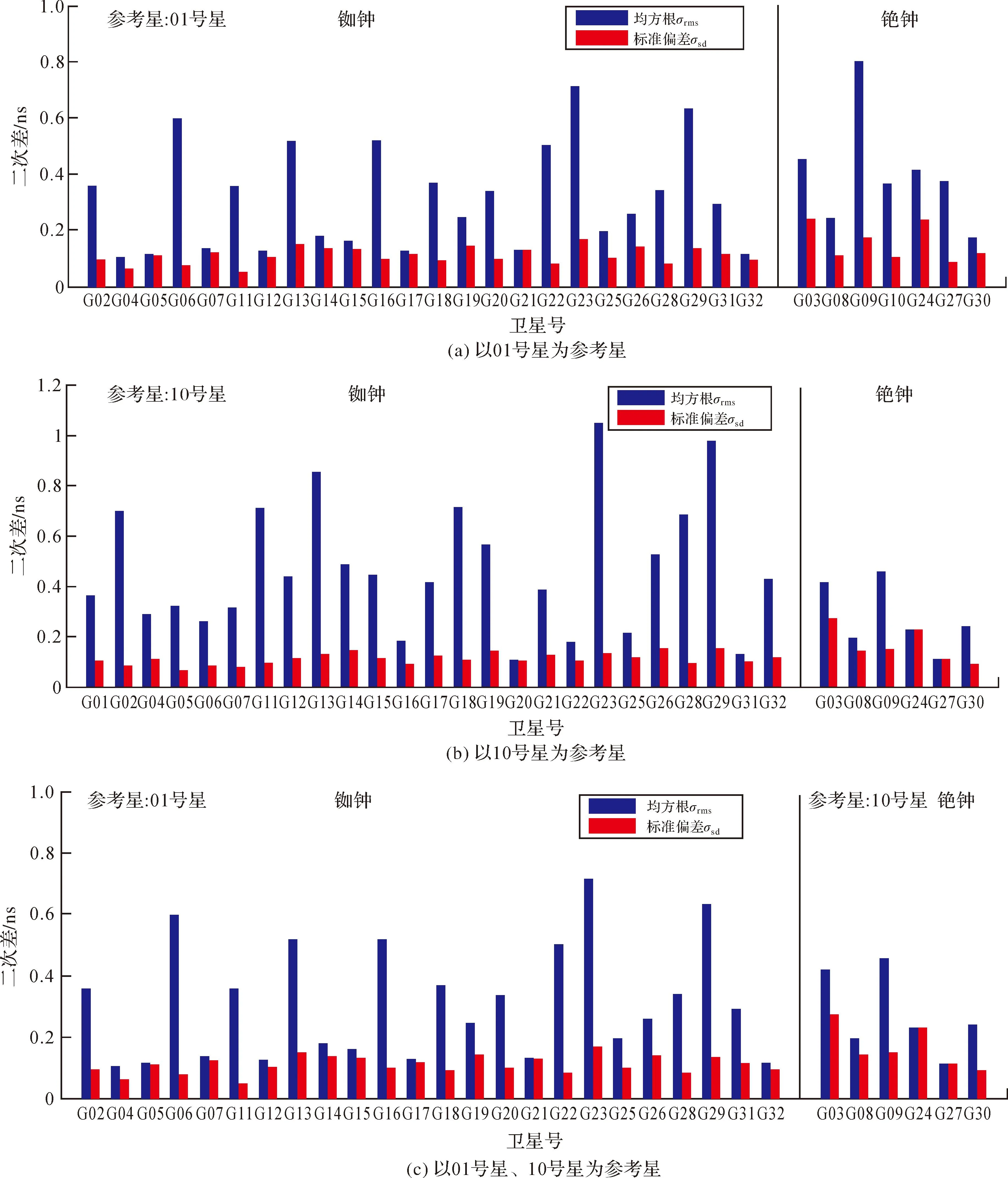
图2　估算的GPS卫星钟差与IGS结果的二次差值

图3为估算的GLONASS卫星钟差与IGL结果，以及Galileo卫星钟差与TUM结果的二次差值，其中GLONASS卫星以01号星为参考星，Galileo卫星以11号卫星为参考星。从图上可以看出，GLONASS卫星钟差精度较低，σrms在6 ns以内，σsd在4 ns左右，分析其原因可能与GLONASS卫星钟自身稳定性较差有关，也可能是钟差估计时采用的误差估计模型或方法有差别导致的；Galileo卫星钟差精度与GPS卫星钟差精度相当，在0.5 ns以内。

图3　估算的GLONASS、GALILEO卫星钟差分别与IGL、TUM结果的二次差值

3. BDS卫星钟差

我国的北斗卫星导航系统目前由14颗组网并提供服务，前5颗为静止轨道卫星，6—10号为倾斜地球同步轨道卫星，最后4颗为中地球轨道卫星。为分析北斗导航系统卫星钟差，本文分别对选择单星基准和多星基准进行研究。

(1) 单星基准

按照各卫星所在轨道类型选择参考星，图4(a)及图4(b)右图分别为以01号星、10号星和14号星为参考星估算的北斗卫星钟差与GFZ结果的二次差值。从图中可以看出，非参考星类型的卫星钟差估计结果的σrms与σsd有明显的系统性偏差，σsd在1 ns以内，而σrms多数已到达6 ns以上，6、7号卫星钟差与同类型的8、9号卫星钟差仍有2 ns的系统性偏差；由图4(b)左图可以看出，当以7号星为参考星时,消除了6号星的系统性偏差。

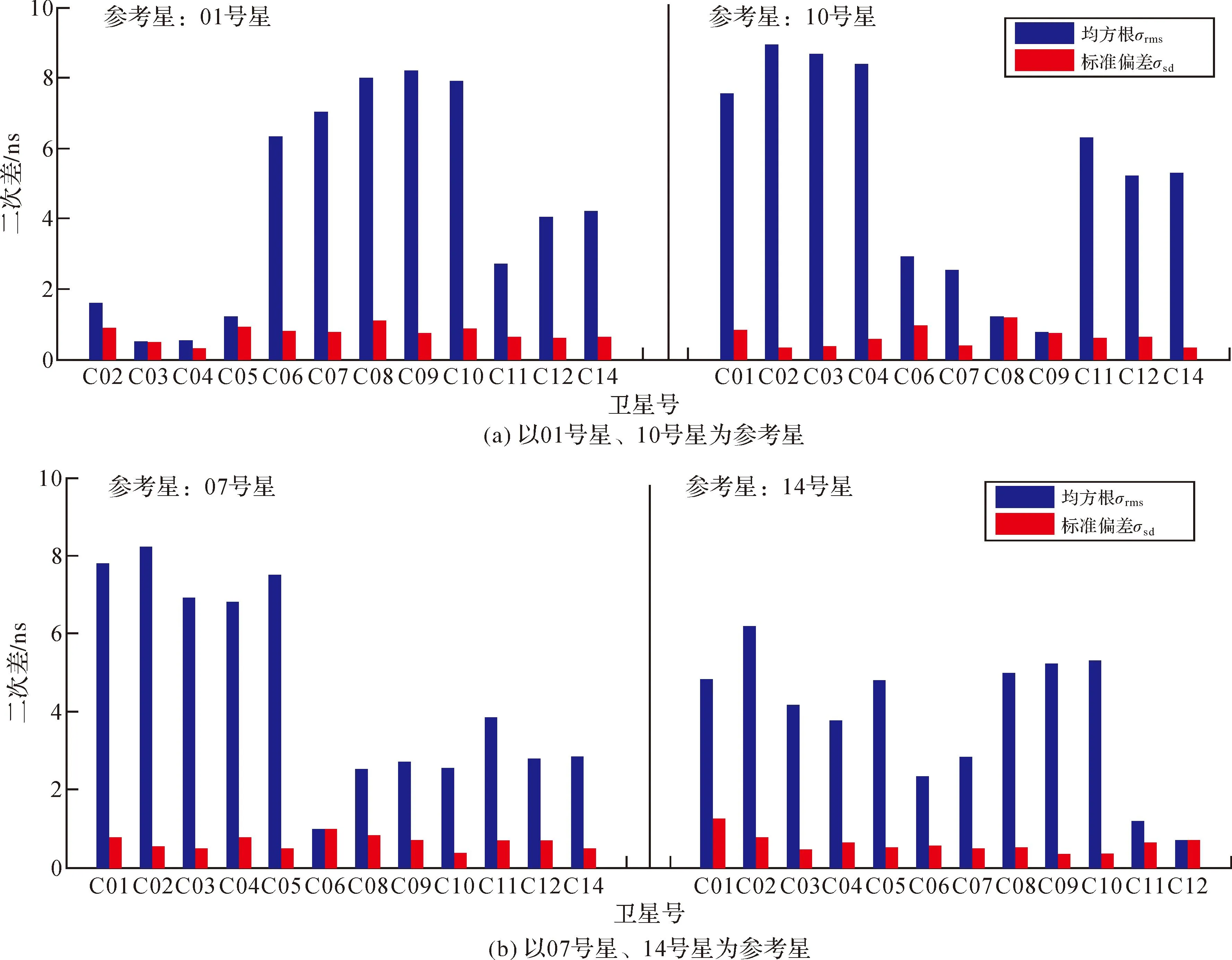
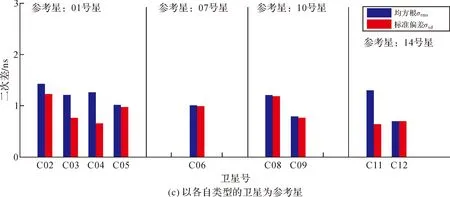
图4　估算的北斗卫星钟差与GFZ结果的二次差值

(2) 多星基准

根据以上对单星基准的分析，图4(c)把北斗导航卫星划分为4类，分别以各自类型的卫星为参考星，可以看出各卫星钟差估计结果的σrms与σsd没有明显的差别，σsd多数都在1 ns以内。这说明北斗各类型卫星之间存在较大的系统性偏差，而本文利用的计算软件也没有完全消除系统偏差，当分别以各自类型的卫星为参考星时，北斗卫星钟差精度在1 ns以内。

三、结束语

目前，我国GNSS分析中心提供的4个导航系统钟差产品的精度基本上与国际相当。中国测绘科学研究院国际GNSS监测评估系统分析中心研发的软件估算的GPS卫星钟差与IGS事后精密钟差互差优于0.2 ns，带有铷钟的GPS卫星钟差比带有铯钟的GPS卫星钟差精度高，稳定性也好，在消除因卫星钟类型不同而对钟差产生的影响后，仍存在0.6 ns的系统性偏差；估算的Galileo卫星钟差精度与GPS卫星相当，在亚纳秒量级；估算的GLONASS卫星钟差精度相对较低，精度在4 ns左右，分析其原因可能与GLONASS卫星钟自身稳定性较差有关，也可能是由本文利用的软件在钟差估计中的误差估计模型或方法与IGL有差别导致的。

我国的北斗卫星导航系统目前有14颗卫星分布在三类轨道上，按照各卫星所在轨道类型选择单星基准时，各类型卫星之间钟差存在较大的系统性偏差，偏差在4 ns左右；选择多星基准可以消除各轨道类型上卫星之间的系统性偏差，消除了偏差之后估算的北斗卫星钟差精度在1 ns以内，但精度仍比GPS卫星钟差低，这可能与北斗系统自身的卫星钟有关。

本文估算的GLONASS卫星钟差精度相对较低，原因有待进一步研究。

参考文献：

[1]党亚民,秘金钟,成英燕.全球导航卫星系统原理与应用[M].北京：测绘出版社，2007.

[2]楼益栋,施闯,周小青，等.GPS精密卫星钟差估计与分析[J].武汉大学学报(信息科学版),2009,34(1):88-91.

[3]罗璠,李建文,黄海，等.北斗卫星钟稳定性分析及噪声识别[J].测绘科学技术学报, 2014(1):34-37.

[4]IGS(2008).IGS Product Availability[EB/OL].[2015-04-20].http:igscb.jpl.nasa.gov.

[5]刘经南,陈俊勇,张燕平，等.广域差分GPS原理和方法[M].北京：测绘出版社, 1999.

[6]郭际明,孟祥广,李宗华，等.GLONASS卫星广播星历精度分析[J].大地测量与地球动力学, 2011,31(1):68-71.

[7]罗小敏,蔡昌盛,戴吾蛟，等. Galileo IOV卫星实时轨道和钟差数据的精度评估[J].测绘通报, 2014(6):1-4.

[8]冯义楷,刘焱雄,单瑞，等.GPS精密卫星钟差的计算模型研究[J].大地测量与地球动力学, 2010,30(2):109-112.

[9]WANG H, WANG C, WANG J X,et al. Global Characteristics of the Second-order Ionospheric Delay Error Using Inversion of Electron Density Profiles from COSMIC Occultation Data[J].China-Phys Mech Astron, 2014(57):365-374.

[10]王宇谱,吕志平,陈正生，等.卫星钟差预报的小波神经网络算法研究[J].测绘学报, 2013,42(3):323-329.

[11]黄观文,杨元喜,张勤.开窗分类因子抗差自适应序贯平差用于卫星钟差参数估计与预报[J].测绘学报, 2011,40(1):15-21.

[12]郭海荣,杨元喜.导航卫星原子钟时域频率稳定性影响因素分析[J].武汉大学学报(信息科学版)， 2009,34(2):218-221.

[13]杨元喜.动态定位自适应滤波解的性质[J].测绘学报, 2003,32(3):189-192.

[14]李玮,程鹏飞,秘金钟. 灰色系统模型在卫星钟差短期预报中的应用[J]. 测绘通报, 2009(6):32-35.

[15]王继刚.基于GPS精密单点定位的时间比对与钟差预报研究[D].北京：中国科学院研究生院, 2010.

中图分类号：P228

文献标识码：B

文章编号：0494-0911(2016)04-0005-05

作者简介：万军(1991—)，男，硕士生，主要从事多系统周跳探测及数据处理方面的研究。E-mail: wanjcasm@163.com

基金项目：国家自然科学基金(41474011；41374014); 国家863计划(2013AA122501); 国家测绘地理信息局基础测绘项目(A1403); 北斗分析中心项目(GFZX0301040308-06); 中国测绘科学研究院学术科研业务费(7771502；7771405)

收稿日期：2015-05-19

引文格式： 万军，党亚民，庞辉，等. GNSS精密卫星钟差估算与分析[J].测绘通报，2016(4)：5-9.DOI:10.13474/j.cnki.11-2246.2016.0110.