基于SVM和LS-SVM的住宅工程造价预测研究
2016-06-01秦中伏雷小龙金灵志
秦中伏,雷小龙,翟 东*,金灵志
(1. 浙江大学 建筑工程学院, 浙江 杭州 310058; 2. 杭州市发展规划研究院, 浙江 杭州 310006)
基于SVM和LS-SVM的住宅工程造价预测研究
秦中伏1,雷小龙1,翟东1*,金灵志2
(1. 浙江大学 建筑工程学院, 浙江 杭州 310058; 2. 杭州市发展规划研究院, 浙江 杭州 310006)
摘要:为在方案设计初期与工程造价相关信息很少的条件下,准确快速地预测住宅工程造价,在分析既往相关理论和方法优劣的基础上,选取支持向量机构建住宅工程造价预测模型,并通过主成分分析对原始数据进行降噪处理. 选取住宅工程造价预测指标集与样本,对输入指标的数据进行主成分分析,消除指标相关性的同时对原始数据降维,将处理后的数据分别导入到“标准支持向量机”和“最小二乘支持向量机”模型中进行训练和预测,并对预测结果进行对比分析,选取较为合理的预测模型,通过参数寻优进一步优化预测效果. 所构建预测模型的相对误差均控制在±7%以内,预测精度较高,结果稳定.
关键词:造价预测;主成分分析;支持向量机;最小二乘支持向量机
QIN Zhongfu1, LEI Xiaolong1, ZHAI Dong1*, JIN Lingzhi2
(1.CollegeofCivilEngineeringandArchitecture,ZhejiangUniversity,Hangzhou310058,China; 2.HangzhouDevelopmentPlanning&ResearchInstitute,Hangzhou310006,China)
建筑工程造价预测是建设项目可行性研究的重要内容,将直接影响建设单位对建设项目的投资决策. 建筑工程的造价预测最初是通过单位指标法[1]套用相应的估算指标计算并汇总而得. 由于估算指标统一,不能很好地适应各类市场经济体制. 在传统的统计分析方法中,线性回归法是通过建立回归分析模型来预测工程造价的,当该方法面对繁多的不确定因素且样本数据较少时表现较差[2]. 时间序列分析法需要的样本数量相对较少,但未能充分考虑建筑工程造价偶然因素繁多且难以估计的特点[3-4].
近年来,基于神经网络、灰色理论等的工程造价预测研究逐渐成熟. 虽然,神经网络算法与传统的统计分析相比,预测效果有一定改善,但仍存在所需样本数量多、训练速度较慢、容易出现局部最优等问题[5-6]. 灰色理论虽然可以在一定程度上解决建筑工程造价预测所面临的小样本问题,但模型参数少,容错性小,不适用于方案设计初期的工程造价预测[7-8].
支持向量机算法(SVM)是基于VAPNIK等[9]建立的统计学习理论(SLT)发展而来的.由于该算法引入了结构风险最小化原理和核函数,因此,与神经网络等传统的机器学习相比,其在小样本学习和非线性问题上表现突出,泛化能力强[10-11]. 由于SVM训练的复杂性,因此,以降低训练时间和计算复杂性的SVM改进算法的研究居多,如块处理算法、SMO算法等[12-13].最小二乘支持向量机(LS-SVM)也是SVM的一种改进算法,用于解决SVM面临的维数灾难,该算法在一定程度上保证SVM预测的鲁棒性和精度的同时,可有效提高机器学习的效率[14-15]. SVM和LS-SVM在工程造价预测应用上各有优劣,研究者大多分别基于SVM和LS-SVM展开预测,很少对比分析两者的预测效果,以选出较为合理的预测模型[16-17].
本研究通过主成分分析将降噪处理的样本数据分别导入到“SVM”和“LS-SVM”模型中进行训练和预测,并对预测结果进行对比分析,进而选出较为合理的预测模型;另外,由于应用SVM算法进行预测时,惩罚系数和核参数等的设定对预测结果影响较大[18-19],因此,本研究将通过参数寻优进一步优化模型的预测效果.
1支持向量机原理
1.1标准支持向量机
支持向量机(SVM)理论是从线性可分情况下的最优分类线[20]发展而来,可以很好地解决建筑工程造价预测所面临的小样本、非线性问题. 最优分类线不仅能够将两类不同的样本分开,且分类间隔最大. 最优分类线上升到多维空间上就变成了最优分类面,寻找最优分类面是一个二次规划问题. 支持向量机在寻找最优分类面时,通过运用核函数将原始空间上线性不可分的样本映射到高维空间进行分类,并运用损失函数引入容错率. 因此,SVM的优化问题为:
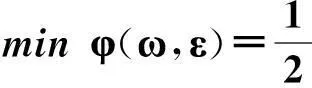
s.t.y1(ωxi+b)=1-εi,
(1)
i=1,2,…,l;εi≥0,
其中,ω为权值系数;b为常值偏差;C为惩罚系数;εi为松弛因子.定义Lagrange函数:
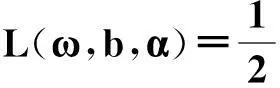
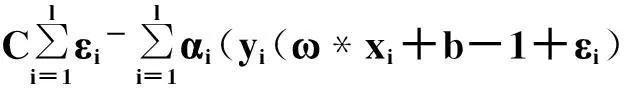
(2)
原二次规划问题转化为:
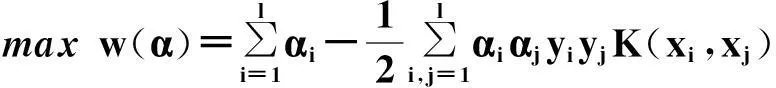
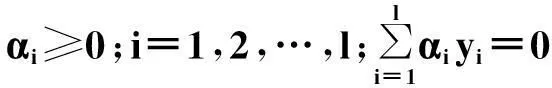
(3)
1.2最小二乘支持向量机
LS-SVM是SVM的一种改进算法,在优化问题的处理上对支持向量机进行了改进,选取了不同的损失函数,将不等式约束条件变为等式约束,因此,LS-SVM的优化问题为:
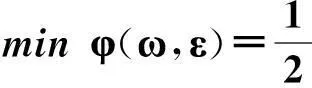
s.t.yi(ωxi+b)=1-εi,
(4)
i=1,2…,l;εi≥0,其中,ω为权值系数;b为常值偏差;C为惩罚系数;εi为松弛因子.
定义Lagrange函数:
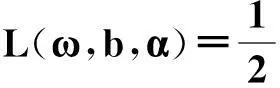
(5)
令ω,b,εi,αi的偏导数等于0,并消去ω,ε可得:
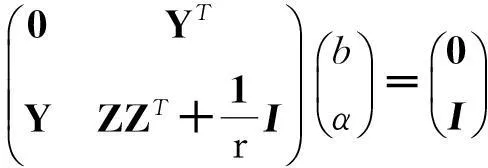
(6)
其中,
ZT=[y1φ(x1),y2φ(x),…,ylφ(xl)],
YT=[y1φ(x1),y2φ(x),…,ylφ(xl)],
IT=[1,2,…,l],αT=[α1,α2,…,αl].
且根据mercer条件[21-22],存在核函数
K(xi,xj)=φ(xi)Tφ(xj)T,
(7)
因此,最小二乘支持向量机的决策函数为:
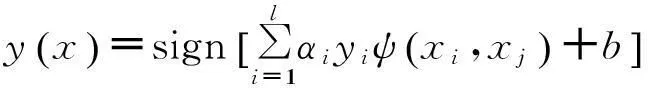
(8)
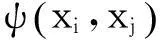
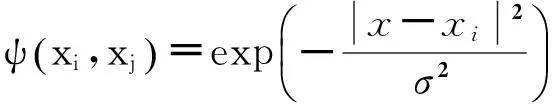
(9)
其中, σ为核函数的参数,与C同在Matlab里通过参数寻优得到.
2住宅工程造价预测指标选取
为了实现“方案设计初期的住宅建筑的毛坯造价”的预测,该阶段建设工程的相关信息量较少,往往只能初步确定该工程的结构与基础等参数.通过查阅文献、结合相关专家意见,并参考文献[25],本研究选取了用于住宅工程造价预测模型构建的指标,所选指标均反映方案设计初期建设工程的基本特征,具体如表1所示.
3基于SVM和LS-SVM的预测模型对比分析
3.1案例说明
本文共收集了26个杭州地区的住宅项目(分别来自不同的地产公司和施工企业).因建筑面积过小的项目其造价易受偶然因素影响,在综合考虑专家意见的基础上,淘汰了其中1个建筑面积小于3×104m2的建设项目,将其余25个项目作为样本,对建筑工程造价预测模型进行仿真分析.
根据表1编号,25个样本工程的造价数据的指标分布如表2所示.
表1住宅工程造价预测指标
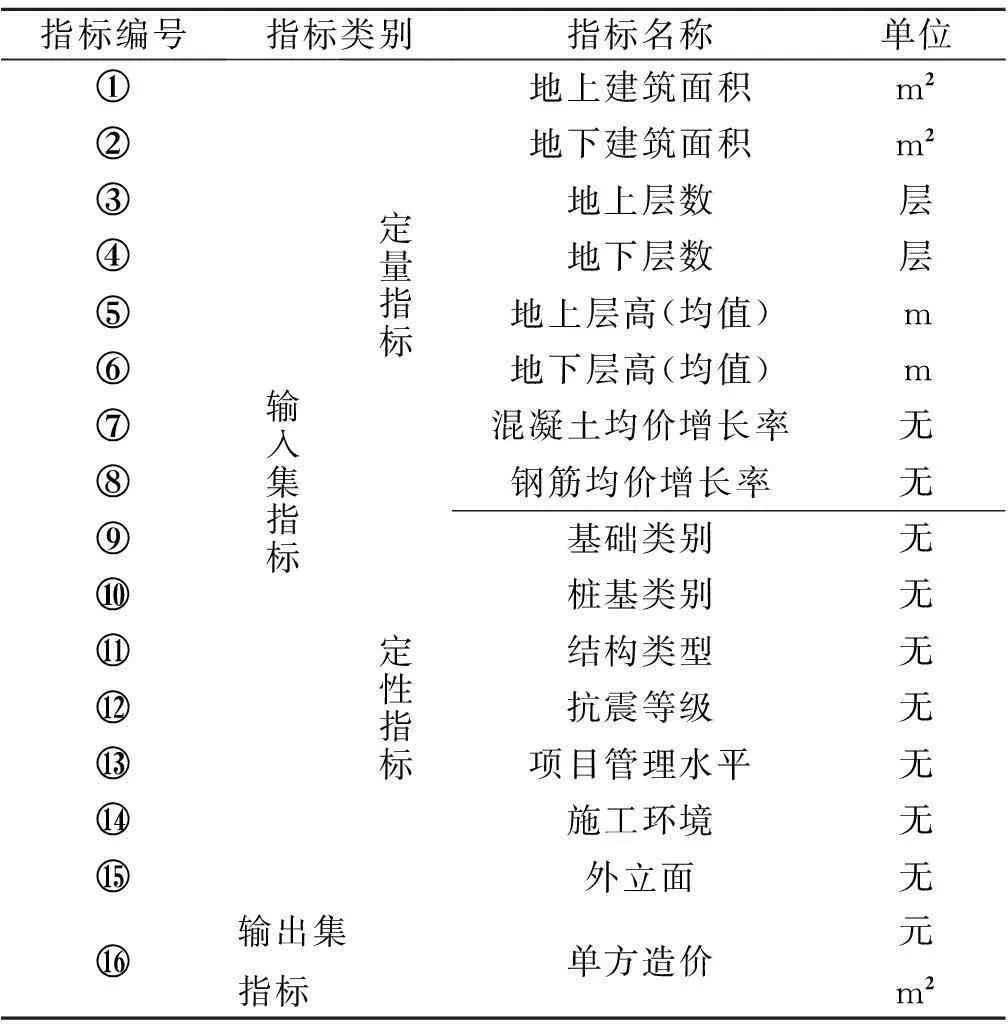
Table 1 The indicators of residential construction
注由于本文是针对建设项目方案设计初期工程造价的预测,因此将文献[25]中的“土方处理难度”指标删除,同时补充“施工环境”指标,该指标信息在项目前期较易获取.
表2样本工程造价数据分布
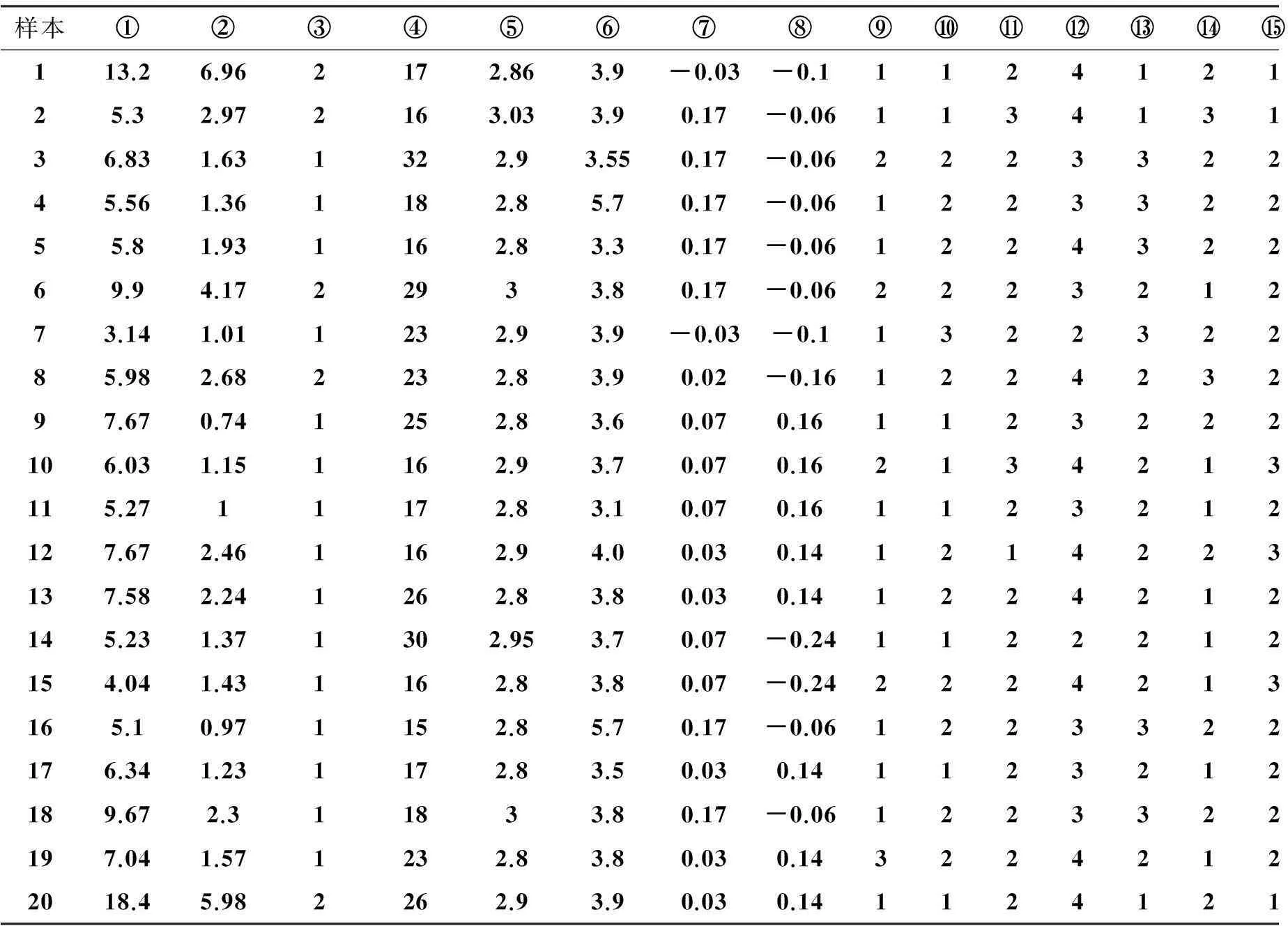
Table 2 Cost of engineering data from different cases
续表2
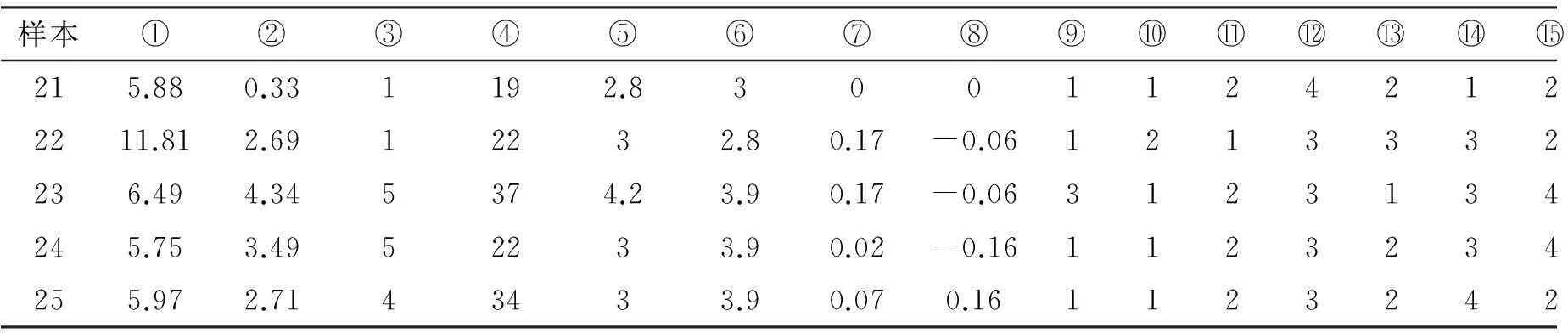
样本①②③④⑤⑥⑦⑧⑨⑩215.880.331192.8300112421216072211.812.6912232.80.17-0.0612133322306236.494.345374.23.90.17-0.0631231342391245.753.4952233.90.02-0.1611232342460255.972.7143433.90.070.1611232422701
3.2主成分分析
对25个样本工程的输入集指标数据进行主成分分析,每个样本有15个变量,构成一个25×15阶矩阵:

(10)
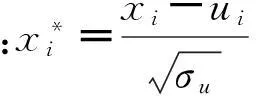
表3主成分的特征值、贡献率和累计贡献率
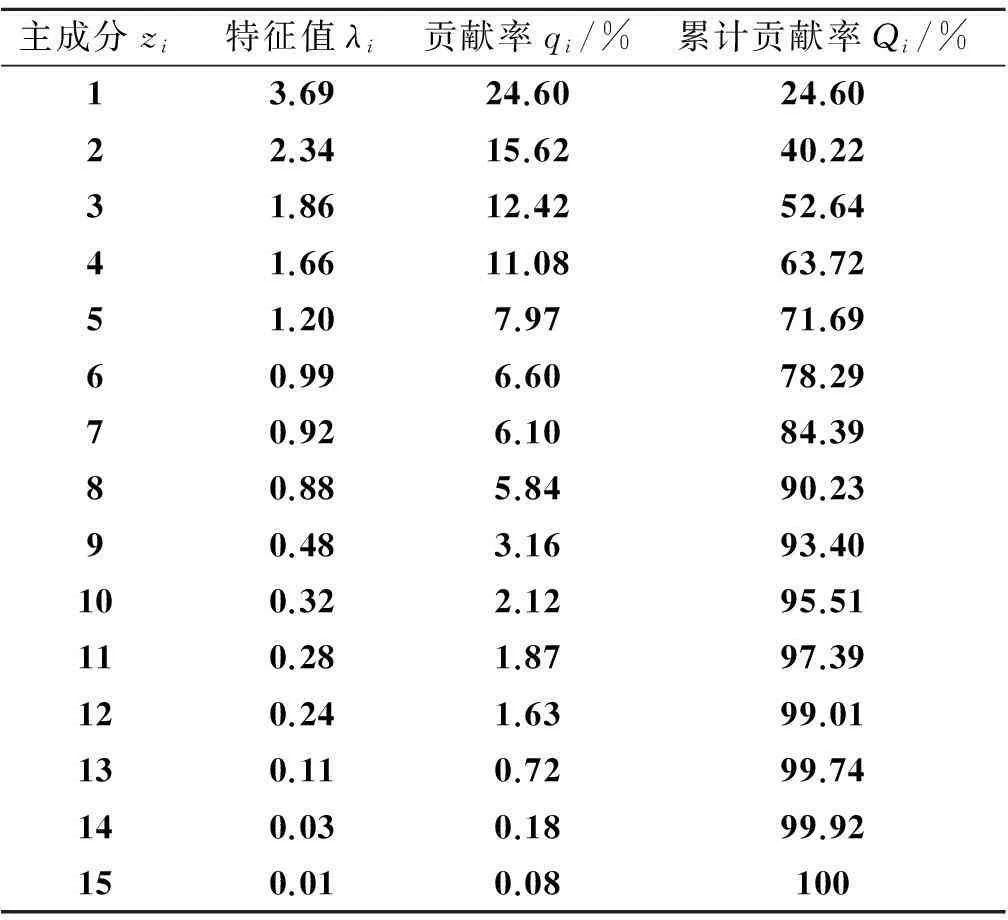
Table 3 The eigenvalue, contribution rate and the cumulative
各主成分的特征值和贡献率从z1到z15依次减小. 一般累计贡献率Qi≥85%时,认为前i个主成分可以代替原始指标信息[16-17,20]. 本研究选取前9个主成分(Q=93.3961%)作为建筑工程造价预测模型的新输入集,用于“基于SVM和LS-SVM的预测模型对比分析”.
3.3预测模型对比分析
首先,将25个样本进行分离,选取前20个样本作为训练样本,剩下的5个样本作为测试样本;其次,在Matlab环境中,将处理后的输入集数据和输出集数据分别导入到SVM和LS-SVM预测模型中,2种支持向量机的起始参数均为:惩罚系数C=100,核函数的宽度系数σ2=0.25;最后,分别导出2种支持向量机的预测结果并进行对比分析. 其中计算机的运行环境为:(1)配置:4 G内存,intel酷睿处理器(i3,2370m),英伟达显卡(GT610M,1 G);(2)软件:Matlab 2009b,预装SVM与LS-SVM工具箱.
图1所示分别为基于SVM和LS-SVM的预测模型的预测曲线.
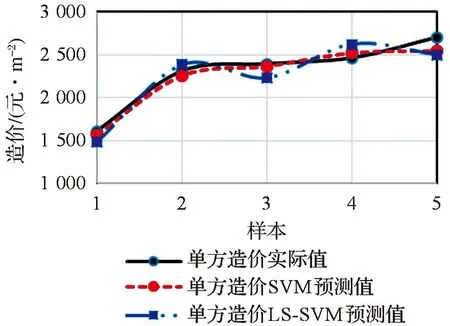
图1 基于SVM和LS-SVM的住宅工程造价预测效果图Fig.1 Forecast effect of housing project cost basedon SVM and LS-SVM
3.3.1精度分析
如表4所示,基于SVM的预测模型预测绝对误差最大为53元·m-2,最小为-163元·m-2,基于LS-SVM的预测模型预测绝对误差最大为159元·m-2,最小为-204元·m-2;基于SVM的预测模型预测相对误差最大为2.15%,最小为-6.03%,基于LS-SVM的预测模型预测相对误差最大为6.46%,最小为-7.78%.
从以上数据中可发现:(1)基于SVM和LS-SVM的住宅工程造价预测的相对误差均控制在±10%以内,满足实际生活中建筑工程造价快速估算的精度要求[24-25,27];(2)基于SVM的住宅工程造价预测模型在相对误差控制上表现更好,因此,其预测精度更高.
3.3.2鲁棒性分析
本研究将通过2种支持向量机模型预测相对误差的极差分析,来进一步分析2种支持向量机模型预测的稳健度.
由表4可知,基于SVM模型预测的相对误差分布区间为[-6.03%,2.15%],其极差为最大值-最小值,即2.15%-(-6.03%)=8.18%. 基于LS-SVM模型预测的相对误差分布区间为[-7.78%,6.46%],其极差为6.46%-(-7.78%)=14.24%.
通过以上分析,可知“基于LS-SVM模型预测的相对误差”的极差相较于“基于SVM模型预测的相对误差”极差要大74.8%,因此,基于SVM的预测模型的预测精度更稳健.
3.3.3预测时间分析
由表4可知,基于SVM预测模型的预测时间为5.43 s,基于LS-SVM预测模型的预测时间为3.45 s;相较于前者,预测时间缩短了36.46%.因此,基于LS-SVM预测模型的预测速度较快,很好地实现了对标准SVM数据处理的算法优化,对SVM所面临的数据灾难进行了降维.
通过以上关于基于SVM和LS-SVM的模型的预测效果对比分析,发现基于LS-SVM的预测模型预测速度较快,其预测时间相较于SVM模型缩短了1.98 s,效率提升36.46%,但是该模型预测精度较低,预测结果也不够稳健.
考虑到现实生活中,“1.98 s”对于一次住宅工程的造价预测影响较小,笔者认为“基于标准SVM的住宅工程造价预测模型”更适用于方案设计初期工程造价的预测.
表4基于SVM和LS-SVM模型的预测效果对比
4预测模型参数寻优
相关研究表明,影响支持向量机性能的关键因素是核函数的参数σ,惩罚系数C,而不是核函数的类型[21-22]. 因此,选择合适的核函数参数和惩罚系数至关重要. 由于惩罚系数和核函数参数之间是相互独立的,为此,本文以径向基函数为核函数的SVM为例,采用“控制变量法”实现参数的寻优.
将25个样本进行分离,选取前20个样本作为预测模型的训练样本,剩下的5个样本作为测试样本;之后,将处理后的数据导入到SVM预测模型中;此时,分别调整该模型所选的参数,并对预测效果进行评估.
4.1惩罚系数寻优
控制核参数σ=0.5不变,惩罚系数C的取值为[50,150]中10的倍数. 本文以预测模型预测的“绝对误差的绝对值的均值(即平均预测偏差)”为纵坐标,衡量模型预测效果与参数选择的关系.
陈小华:是58到家旗下子公司,未来自己融资,自己做IPO。在中国的公司里面,一直讲一拆就散,一合就死,战略协同很难做。不过未来58到家的子公司,都会是58到家集团的一分子,所有战略都会协同,各个业务的CEO首先是集团的高管,其次才是业务的CEO。
从图2可见,随着惩罚系数C的增大,预测模型的平均偏差逐渐减小,即模型预测效果逐渐变好. 但模型结构风险最小化趋向于经验风险最小化,因此在模型预测精度提高的同时,其泛化能力却逐渐降低,且模型复杂度逐渐提高. 为此,本文选取惩罚系数C=100作为模型参数寻优的结果.
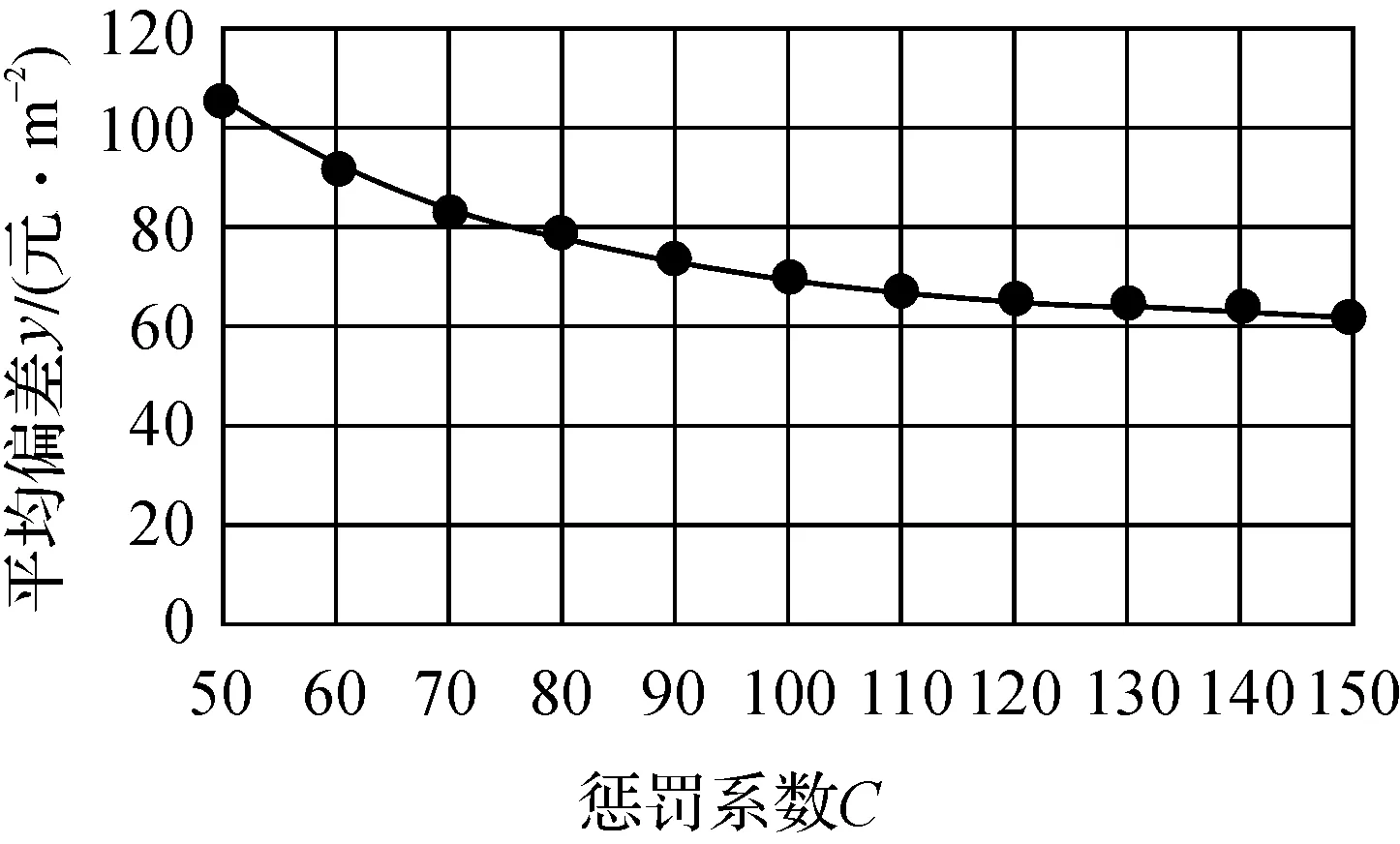
图2 惩罚系数C与预测平均偏差的关系Fig.2 Relationship between penalty coefficient Cand average deviation
4.2核参数寻优
控制惩罚系数C=100不变,核参数的取值为[0.1,1.0]中0.1的倍数. 本文以预测模型预测的“绝对误差的绝对值的均值(即平均预测偏差)”为纵坐标,衡量模型预测效果与参数选择的关系.
如图3所示,随着核参数的增大,预测模型的平均偏差先减小后增大,即模型预测效果先逐渐变好后又逐渐变差. 当核参数取某一中间值时,预测模型表现出最佳的预测效果. 根据图3核参数与预测平均偏差的关系,本文选取σ=0.4为模型核参数寻优的结果.
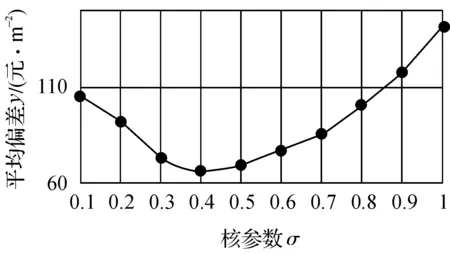
图3 核参数与预测平均偏差的关系Fig.3 Relationship between kernel parameterand average deviation
通过以上分析,所获取的最优参数组合为:惩罚系数C=100,核参数σ=0.4.
4.3最优参数组合下预测模型仿真分析
取25个样本中的前20个作为训练样本,其余5个作为测试样本;在Matlab环境中,将经PCA处理后的数据导入到SVM模型中,设定参数:惩罚系数C=100,核参数σ=0.4. 预测结果如表5所示,可知惩罚系数C=100,核参数σ=0.4时,模型预测相对误差在[-5.70%,2.07%]. 预测精度和稳健度较核参数σ=0.5时有进一步提高.
表5最优参数组合下模型的预测效果
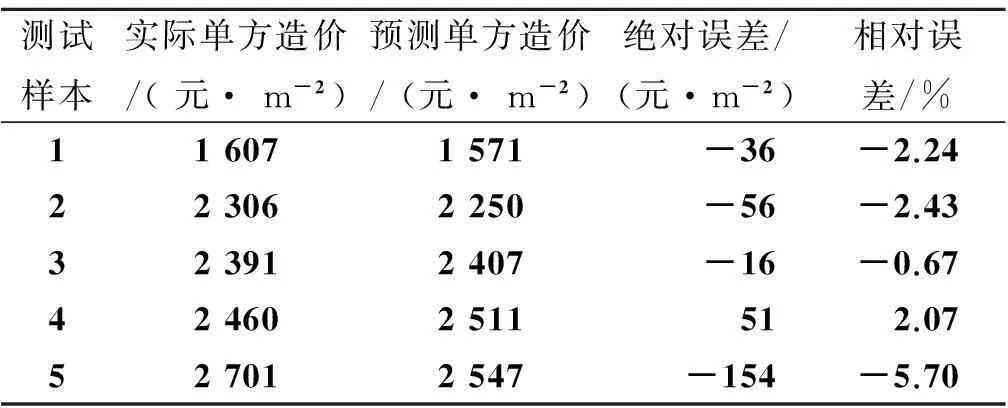
Table 5 Prediction effect of the optimal parameter
5结论
基于SVM和LS-SVM 2种模型在造价预测上的优劣分析,将通过主成分分析进行降噪处理的样本数据分别导入到“SVM”和“LS-SVM”模型中进行训练和预测,并对预测结果进行对比分析,选取较为合理的预测模型,更好地实现方案设计初期的住宅工程造价预测.通过对比分析,发现基于标准SVM的预测模型的预测精度较高,且结果稳健. 另外,通过控制变量法实现了对标准SVM模型的惩罚系数C和核参数σ值的选取,进一步论证了惩罚系数与核参数对SVM性能的重要影响.
参考文献(References):
[1]毛义华.建筑工程经济[M].杭州:浙江大学出版社,2012:145.
MAO Yihua.Construction Economy[M]. Hangzhou:Zhejiang University Press, 2012:145.
[2]薛向阳.一种改进的线性回归预测模型[J].科学技术与工程,2010,10(12):2970-2973.
XUE Xiangyang. Improved linear regression forecast model[J].Science Technology and Engineering,2010,10(12):2970-2973.
[3]KAYACAN E, ULUTAS B, KAYNAK O. Grey system theory-based models in time series prediction[J]. Expert Systems with Applications,2010,37(2):1784-1789.
[4]余昕.基于数据挖掘的时间序列预测的研究与应用 [D]. 北京:中国地质大学,2011.
YU Xin. Research and Application on Time Series Prediction Based on Data Mining Method[D]. Beijing:Chinese University of Geosciences,2011.
[5]陈智勇, 廉海涛, 吴星星.一种改进的神经网络分支预测技术[J].微电子学与计算机,2014,31(11):152-155.CHEN Zhiyong, LIAN Haitao,WU Xingxing. An improved branch prediction based on the neural network[J]. Microelectronics and Computer,2014,31(11):152-155.
[6]祝文娟.基于遗传模糊神经网络的建筑工程造价估算模型[D].焦作:河南理工大学,2010.
ZHU Wenjuan. Building Project Cost Estimate Model Based on Genetic Fuzzy Neural Network[D]. Jiaozuo:Henan Polytechnic University,2010.
[7]YIN M S. Fifteen years of grey system theory research: A historical review and bibliometric analysis[J]. Expert Systems with Applications,2013,40(7):2767-2775.
[8]孙涛.灰色系统预测理论在建筑工程造价中的应用 [D].西安:西北工业大学,2006.
SUN Tao. Gray Forecast Theory in the Construction Costs[D]. Xi’an: Northwestern Polytechnical University,2006.
[9]VAPNIK V N. Statistical Learning Theory[M]. New York: John Wiley,1998:34-42.
[10]ALDRICH C, AURET L. Statistical learning theory and kernel-based methods[C] // Unsupervised Process Monitoring and Fault Diagnosis with Machine Learning Methods. London: Springer , 2013: 117-181.
[11]蒋丽娜.基于支持向量机的建筑工程造价预测研究[D]. 邯郸: 河北工程大学,2009.JIANG Lina. Research on the Predict of the Construction Cost Based on Support Vector Machine[D]. Handan: Hebei University of Engineering,2009.
[12]白鹏,张喜斌,张斌. 支持向量机理论及工程应用实例 [M].西安:西安电子科技大学出版社, 2008:13-36.
BAI Peng, ZHANG Xibin, ZHANG Bin. Support Vector Machine Theory and Engineering Application Examples[M]. Xi’an:: Xidian University Press, 2008:13-36.
[13]PENG X. TSVR: An efficient twin support vector machine for regression[J]. Neural Networks,2010,23(3):365-372.
[14]SUYKENS J A K, VANDEWALLE J. Least squares support vector machine classifiers[J]. Neural Processing Letter,1999(3):293-300.
[15]邢永忠.最小二乘支持向量机的若干问题与应用研究[D].南京: 南京理工大学,2009.
XING Yongzhong. A Number of Problems and Applications of the Least Squares Support Vector Machine[D]. Nanjing: Nanjing University of Science and Technology, 2009.
[16]彭光金,俞集辉,韦俊涛,等.特征提取和小样本学习的电力工程造价预测模型[J].重庆大学学报,2009,32(9):1104-1110.
PENG Guangjin, YU Jihui, WEI Juntao, et al. Cost forecast model for power engineering based on feature extraction and small-sample learning[J].Journal of Chongqing University,2009,32(9):1104-1110.
[17]申瑞娜,曹昶,樊重俊.基于主成分分析的支持向量机模型对上海房价的预测研究[J].数学的实践与认识,2013,43(23):11-16.SHEN Ruina, CAO Chang, FAN Chongjun. Support vector machine model based on principal component analysis for the Shanghai real estate price of prediction[J]. Mathematics in Practice and Theory,2013,43(23):11-16.
[18]刘健. 基于支持向量机的在线学习算法研究[D]. 杭州:浙江大学,2013.
LIU Jian. Study on the Online Learning Algorithm Based on Support Vector Machine[D]. Hangzhou: Zhejiang University,2013.
[19]顾燕萍,赵文杰,吴占松.最小二乘支持向量机的算法研究[J].清华大学学报:自然科学版,2010(07):1063-1066,1071.
GU Yanping, ZHAO Wenjie, WU Zhansong. Algorithm for least squares support vector machine[J]. Journal of Tsinghua University :Natural Science Edition, 2010(07):1063-1066,1071.
[20]ABDI H, WILLIAMS L J. Principal component analysis[J]. Wiley Interdisciplinary Reviews: Computational Statistics,2010,2(4):433-459.
[21]CRISTIANINI N, SHAWE-TAYLOR J. An Introduction to Support Vector Machines and Other Kernel-Based Learning Methods [M]. Cambridge: Cambridge University Press,2000:30-34.
[22]BOOLCHANDANI D, SAHULA V. Exploring efficient kernel functions for support vector machine based feasibility models for analog circuits[J].International Journal on Design Analysis and Tools for Circuits and Systems,2011,1(1):1-8.
[23]王东, 史晓霞, 尹交英. 不同核函数的支持向量机用于空调负荷预测的对比研究[J].电工技术学报,2015(S1):531-535.
WANG Dong, SHI Xiaoxia, YIN Jiaoying. Different kernel function of support vector machine for air conditioning load forecasting contrast[J]. Electrotechnical Journal,2015(S1):531-535.
[24]PRAJAPATI G L, PATLE A. On performing classification using SVM with radial basis and polynomial kernel functions[C]// Emerging Trends in Engineering and Technology(ICETET)- 3rd International Conference on IEEE,Washington:IEEE Computer Society,2010: 512-515.
[25]杨锦跃.基于BP神经网络的建筑工程造价预测研究[D]. 杭州:浙江大学, 2015.
YANG Jinyue. BP Neural Network Based on the Construction Project Cost Prediction Research[D]. Hangzhou: Zhejiang University, 2015.
[26]陈佩. 主成分分析法研究及其在特征提取中的应用[D]. 西安:陕西师范大学,2014.
CHEN PEI. Principal Component Analysis Method and its Application in Feature Extraction [D]. Xi’an: Shaanxi Normal University, 2014.
[27]雷雨.基于改进 BP神经网络的工程造价估算研究[D].西安:西安建筑科技大学,2013.
LEI Yu. Engineering Cost Estimation Research Based on Improved BP Neural Network[D].Xi’an: Xian University of Architecture and Technology,2013.

Forecasting the costs of residential construction based on support vector machine and least squares-support vector machine. Journal of Zhejiang University(Science Edition), 2016,43(3):357-363
Abstract:To forecast the costs of a residential construction rapidly and accurately at the initial stage of construction that lacks relevant information, in view of the strengths and weaknesses of previous approaches, we choose support vector machine (SVM) and principal component analysis (PCA). Firstly, a residential project cost forecasting index set is selected; The data of the input index is then analyzed and the correlation is eliminated by PCA; Thirdly, the processed data are imported into the standard support vector machine and trained by the least squares support vector machine model. The prediction results are compared and analyzed, and then a more reasonable prediction model is adopted; Finally, the prediction result of the model is optimized by model parameter optimization. Experiments show that the relative error of the prediction model is controlled within ±7%, and the result is stable.
Key Words:construction cost forecasting; principal component analysis; support vector machine; least squares support vector machine
中图分类号:TU -9
文献标志码:A
文章编号:1008-9497(2016)03-357-07
作者简介:秦中伏(1965-),ORCID:http://orcid.org//0000-0003-3894-1263,男,副教授,博士,主要从事人工智能、建筑经济等研究,E-mail:qinzhongfu@zju.edu.cn.*通信作者,ORCID:http://orcid.org//0000-0001-5309-060X,E-mail:0012078@zju.edu.cn.
基金项目:国网浙江省电力公司经济技术研究院资助项目(12-513205-007,名称:输电线路工程造价预测快速实现).
收稿日期:2015-11-30.
DOI:10.3785/j.issn.1008-9497.2016.03.017
