点到代数曲线最短距离的细分算法

祁佳玳， 寿华好

(浙江工业大学 理学院, 浙江 杭州 310023)



点到代数曲线最短距离的细分算法

祁佳玳， 寿华好*

(浙江工业大学 理学院, 浙江 杭州 310023)

摘要：距离计算在计算机辅助几何设计与图形学领域有着广泛的应用. 为了有效计算点到代数曲线的最短距离，提出了一种基于区间算术和区域细分的细分算法.利用四叉树数据结构对给定区域进行细分，用区间算术计算细分后所有像素点到给定点的距离区间，得到最小距离区间.该方法的优势在于在得到任意精度的点到代数曲线最短距离的同时，亦得到了该结果的最大误差限.为进一步提高速度，还对算法进行了改进.

关键词：代数曲线；最短距离；区间算术；细分算法

0引言

距离计算有着广泛的应用，如计算机图形学及游戏中的碰撞检测、CAD/CAM中的干涉检测、几何造型中点到曲线距离的查询等.此外，距离计算还广泛应用于计算机仿真、触觉仿真、机器人路径规划等.关于距离计算的研究亦从未中断过.

CHANG 等[1]基于剔除技术提出了一种有效且稳定的方法，计算2条Bézier曲线及2张Bézier曲面之间的最短距离.该方法充分利用控制顶点凸包的最近点对，提出了一种新的节点分割方法.MA等[2]通过将一系列圆锥球作为包围盒，提出了有效计算2张管道曲面距离的方法：用圆锥球包围盒之间的距离近似为2张管道曲面的距离.

陈小雕等[3]首先将得到的一些区间的单向Hausdorff距离作为Hausdorff距离的下界，然后消除上界比该下界小的子区间，提出用几何裁剪法计算2条B-spline曲线的Hausdorff距离，并提出了Hausdorff距离是否发生在两曲线端点的判断条件，该条件把2条曲线间Hausdorff距离的计算转换成点和曲线的最大最小距离，具有较高的稳定性.陈小雕等[4]在稳定的曲线、曲面分裂技术和基于常半径滚动球的几何裁剪算法的基础上，提出了计算Bézier曲线曲面间最近距离的混合算法：首先判断曲线段或曲面片是否包含最近点，此条件可摒弃大部分不包含最近点的曲线段或曲面片；然后判断最近点是否落在曲线的端点或曲面的边界曲线上，将曲线/曲面间的距离计算问题转换成点/曲面或曲线/曲线之间的距离问题，大大降低了问题的复杂度，提高了计算效率. CHEN 等[5]提出了用裁剪圆算法计算点到NURBS曲线的最短距离.以曲线外一定点与该曲线的距离平方作为目标函数，以该定点为裁剪圆圆心，获得裁剪圆初始半径，并利用裁剪圆排除裁剪圆外部的曲线段，有效提高了算法的效率和稳定性. 陈小雕等[6]根据一条曲线上的最近点是另一条曲线的等距曲线与该曲线的切点这一几何特征，基于等距思想提出了计算2条平面代数曲线间最近距离的方法. 该方法同样可用于计算代数曲线和参数曲线之间的最短距离.

LENNERZ等[7]提出了计算边界是二次曲线的二次曲面片之间最小距离的方法.将距离计算问题转换为次数不超过8的单变量多项式的求解问题. KIM[8]根据2张曲面间最近点法向平行的几何特性，提出了计算管道曲面与简单曲面间最小距离的算法. 管道曲面的脊柱曲线和半径函数确定了曲面的特征圆，该特征圆上点的法向形成的一个顶点为脊柱曲线上的点，轴与脊柱曲线上点的切线平行的圆锥，得到该管道曲面与简单曲面间的垂线. 由此建立方程并求解，即可得到最小距离.

余正生等[9]基于隐式曲线曲面的几何特性，分别利用点到曲线的最短距离矢量与曲线上对应点的切向量垂直以及定点到隐式曲面的最短距离矢量与曲面上对应点的法向量平行的事实，得到相应的方程组. 而对于方程组的求解则应用了计算复杂度较低的离散牛顿法，提高了算法的稳定性.

寿华好等[10]基于区间算术和细分算法计算2条代数曲线间的Hausdorff距离.首先利用四叉树数据结构和区间算术对代数曲线进行离散，找到包含这2条代数曲线的全部像素点的集合，然后利用区间算术计算离散化之后的矩形的Hausdorff距离，最后得到距离区间，取该区间的中点为2条代数曲线间Hausdorff距离的近似值，且误差不超过该区间长度的一半.

伍丽峰等[11]提出基于几何特征的快速迭代法、格点法计算点到空间参数曲线的最小距离，并进行了分析比较. 林意等[12]提出把参数曲线离散成折线，将参数曲线间Hausdorff距离的计算转换成折线间Hausdorff距离的计算. 廖平等[13]通过将参数曲线离散成曲线段，提出了点到平面曲线最小距离的分割逼近算法.

本文利用区间算术和细分算法计算点到代数曲线的最短距离区间，将该区间的中点作为点到代数曲线的最短距离的近似值，同时得到了相应的最大误差限. 与已有的算法相比，本算法在得到距离近似值的同时亦得到了误差限，而且理论上精度可以无限高，当然精度越高，花费的时间也越长.

1点到代数曲线最短距离的细分算法

1.1算法原理

1.2算法步骤

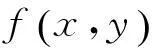
Step3利用四叉树方法，过中心点将该矩形平面区域分成4个小矩形，再对每个小矩形区域重复step1，直到得到的矩形长、宽都小于等于给定的条件ε为止，如果此时还存在排除不掉的矩形区域，则把它们保存在result1中；

Step4考虑result1中的所有矩形区域，若曲线过该矩形区域的2条边，即认为曲线穿过该矩形区域，可以去掉对最小距离计算没有作用的矩形区域，保留曲线穿过的矩形区域；

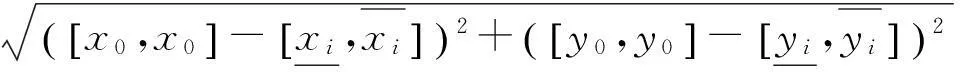
1.3计算实例

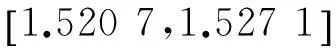
从例1和例2可以看出，当终止条件ε无限小时，所得到的点到代数曲线的最短距离可以无限接近于精确值，误差可达任意小.

2与其他算法的比较

2.1直接计算法

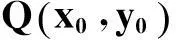
(1)

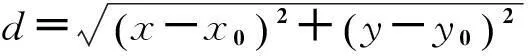
(2)

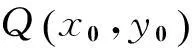
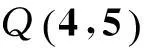
2.2利用四叉树解方程组(本文算法的改进)

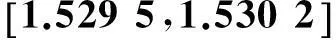
从计算结果可以看出，改进后算法的计算速度有较大的提升.

2.3拉格朗日乘数法

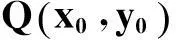
(3)

2.4离散牛顿法

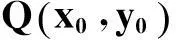
而代数曲线是一种特殊的隐式曲线，因此该算法同样适用于点到代数曲线最短距离的计算.

2.5基于几何特征的快速迭代法

代数曲线在一定条件下可以表示成参数曲线，因此该算法也可应用于求解点到代数曲线的最短距离.

(4)

通过编程实现，选取ε=0.05，当选取参数u=2.42时，得到的最短距离为1.524 6，运行时间为0.043 000 s；当选取参数u=2.43时，得到的最短距离为1.521 4，运行时间为0.044 000 s；当选取参数u=2.435时，得到的最短距离为1.520 3，运行时间为0.058 000 s；当选取参数u=2.437时，得到的最短距离为1.520 0，运行时间为0.057 000 s；当选取参数u=2.437 7时，得到的最短距离为1.519 9，运行时间为0.052 000 s；当选取参数u=2.438时，得到的最短距离为1.519 9，运行时间为0.053 000 s.当选取参数u=3时，得到的最短距离为3.629 9，运行时间为0.007 000 s.

虽然该算法可以得到比较好的结果，但对初始点的要求比较苛刻，若初始点选取不当，得到的结果可能会陷入局部极值，此外，误差也无法得到.

2.6格点法

在点到代数曲线的最短距离问题中，首先需要对代数曲线进行参数化，转变为参数曲线. 目标函数为

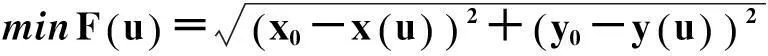
2.7曲线离散成折线法

林意等[12]通过把参数曲线离散成折线，将曲线间Hausdorff距离的计算转换成折线间Hausdorff距离的计算，进一步转换成点到线段之间的Hausdorff距离计算.

通过代数曲线参数化及把参数曲线离散成折线，点到参数曲线的最短距离转换成点到线段的距离. 过该点向线段作垂线，若垂足在线段内，则点到线段的最短距离就是该点到垂足的距离，否则，即为该点到线段两端点的距离的最小值. 对例1进行编程实现，取0为初始点，当取得步长为0.5时，得到的最短距离为1.520 5，运行时间为0.012 000s；当取得步长为0.25时，得到的最短距离为1.520 3，运行时间为0.029 000s；当取得步长为0.1时，得到的最短距离为1.520 1，运行时间为0.052 000s；当取得步长为0.05时，得到的最短距离为1.520 0，运行时间为0.091 000s；当取得步长为0.02时，得到的最短距离为1.519 9，运行时间为0.174 000s,误差无法得到.

2.8曲线离散成曲线段法

廖平[13]提出了把参数曲线离散成曲线段，首先计算定点到每个曲线段端点的距离，记录其中的最小值所对应的点，然后把该点相邻的2个曲线段等分成4份，再记录该点到曲线段端点距离最小值所对应的点，如果该点相邻的2个曲线段2个端点间的参数方向间距小于计算精度，计算结束；否则继续将该点相邻的2个曲线段等分为4份，重复上述步骤.

首先把代数曲线参数化，对例1进行编程实现，取计算精度为0.1，当把曲线等分成20个曲线段时，得到的最小距离为1.520 7，运行时间为0.004 000s；当把曲线等分成30个曲线段时，得到的最小距离为1.520 7，运行时间为0.014 000s；当把曲线等分成50个曲线段时，得到的最小距离为1.520 7，运行时间为0.017 000s；当把曲线等分成100个曲线段时，得到的最小距离为1.520 0，运行时间为0.028 684s,误差无法得到.

以上实例可以看出，本算法可以有效计算点到代数曲线的最短距离，其优势在于得到最短距离近似值的同时得到了该近似值的最大误差限. 这对解决实际问题至关重要.

3结束语

基于区间算术和四叉树区域细分提出了一种计算点到代数曲线最短距离的细分算法，该算法不仅可以有效计算点到代数曲线的最短距离，同时还可得到该结果的最大误差限. 另外，根据终止条件ε的不同，可以得到不同的细分结果，且随着ε趋于无穷小，所得结果的误差可以达到任意小，但计算时间会相对长一些，这也是本算法的不足之处. 为了进一步提高算法的计算速度，对算法进行了改进，从实例中可以看出，改进后计算速度有较大提升.

参考文献(References)：

[1]CHANG Jungwoo, CHIO Yiking, KIM Myungsoo, et al. Computation of the minimum distance between two Bézier curves/surfaces [J]. Computer & Graphics,2011,35(3):677-684.

[2]MA Yanpeng, TU Changhe, WANG Wenping. Distance computation for canal surfaces using cone-sphere bounding volumes [J]. Computer Aided Geometric Design,2012,29(5):255-264.

[3]CHEN Xiaodiao, MA Weiyin, XU Gang . Computing the Hausdorff distance between two B-spline curves[J]. Computer Aided Design,2010,42(12):1197-1206.

[4]陈小雕，王毅刚，徐岗.Bézier曲线曲面间最近距离的几何裁剪算法[J].计算机辅助几何设计与图形学学报,2009,21(10):1404-1411.

CHEN Xiaodiao, WANG Yigang, XU Gang. Geometric pruning method for computing minimum distance between a Bézier curves and a Bézier surfaces [J]. Journal of Computer-Aided Design & Computer Graphics,2009,21(10):1404-1411.

[5]CHEN Xiaodiao, YONG Junhai, WANG Guozhao, et al. Computing the minimum distance between a point and a NURBS curve [J]. Computer-Aided Design,2008,40(10/11):1051-1054.

[6]陈小雕，雍俊海，汪国昭.平面代数曲线间最短距离的计算[J].计算机辅助几何设计与图形学学报,2008,20(4):459-463.

CHEN Xiaodiao, YONG Junhai, WANG Guozhao, et al. Computing the minimum distance between two planar algebraic curves [J]. Journal of Computer-Aided Design & Computer Graphics,2008,20(4):459-463.

[7]CHRISTIAN L, ELMAR S. Efficient distance computation for quadratic curves and surfaces [C] // Proceeding of Geometric Modeling and Processing. New York: IEEE Computer Society Press,2002:60-69.

[8]KIM Kujin. Minimum distance between a canal surface and a simple surface [J]. Computer-Aided Design,2003,35(10):871-879.

[9]余正生，樊丰涛，王毅刚.点到隐式曲线曲面的最小距离[J].工程图学学报,2005(5):74-79.

YU Zhengsheng, FAN Fengtao, WANG Yigang. The minimum distance between a point and an implicit curve/surface [J]. Journal of Engineering Graphics,2005(5):74-79.

[10]寿华好，黄永明，闫欣雅，等.两条代数曲线间Hausdorff距离的计算[J].浙江工业大学学报,2013,41(5):574-577.

SHOU Huahao, HUANG Yongming, YAN Xinya, et al. Computation of the Hausdorff distance between two algebraic curves [J]. Journal of Zhejiang University of Technology,2013,41(5):574-577.

[11]伍丽峰，陈岳坪，谵炎辉，等.求点到空间参数曲线最小距离的几种算法[J].机械设计与制造，2011,32(9):15-17.

WU Lifeng, CHEN Yueping, ZHAN Yanhui, et al. Algorithms on calculating minimum distance between point and spatial parametric curves [J]. Machinery Design & Manufacture,2011,32(9):15-17.

[12]林意，薛思骐，郭婷婷.一种参数曲线间Hausdorff距离的计算方法[J].图学学报，2014，35(5):704-708.

LIN Yi, XUE Siqi, GUO Tingting. A method of calculating the Hausdorff distance between parametric curves [J]. Journal of Graphics,2014,35(5):704-708.

[13]廖平.分割逼近法快速求解点到复杂平面曲线最小距离[J].计算机工程与应用,2009,45(10):163-164.

LIAO Ping. Fast calculating minimum distance between point and complex curve with subdivision approximating algorithm [J]. Computer Engineering and Application,2009,45(10):163-164.

[14]SHOU Huahao, LIN Hongwei, RALPH M , et al. Modified affine arithmetic is more accurate than centered interval arithmetic or affine arithmetic [J]. Lecture Notes in Computer Science,2003,2768:355-365.

QI Jiadai , SHOU Huahao
(CollegeofScience,ZhejiangUniversityofTechnology,Hangzhou310023,China)
A subdivision algorithm for computing the minimum distance between a point and an algebraic curve. Journal of Zhejiang University(Science Edition), 2016,43(3):286-291

Abstract:The distance computation has wide applications in computer-aided geometric design and graphics. A subdivision algorithm based on the interval arithmetic and quadtree data structure for computing the minimum distance between a point and an algebraic curve is proposed . A quadtree data structure is adopted during the subdivision of the give domain, and the interval arithmetic is used to compute the interval distances between the pixel on the algebraic curve and the given point. Compared with other methods, this method can obtain a close approximate value of the minimum distance between a point and an algebraic curve at any precision, while conducting the error estimation at the same time. An improved algorithm is also proposed to further accelerate the calculation speed.

Key Words:algebraic curves; minimum distance; interval arithmetic; subdivision algorithm

中图分类号：TP 391.7

文献标志码：A

文章编号：1008-9497(2016)03-286-06

作者简介：祁佳玳(1992-)，ORCID:http://orcid.org/0000-0003-4909-854X,女，硕士研究生，主要从事计算机辅助几何设计与图形学研究.*通信作者，ORCID:http://orcid.org/0000-0002-8991-337X,E-mail:shh@zjut.edu.cn.

基金项目：国家自然科学基金资助项目(61572430，61272309，61472366).

收稿日期：2015-11-06.

DOI:10.3785/j.issn.1008-9497.2016.03.006