基于三角形模糊数的非线性T-S模糊系统的峰值点和分量半径优化

王宏志, 陶玉杰, 王贵君

(1. 通化师范学院 数学学院, 吉林 通化 134002; 2.天津师范大学 数学科学学院, 天津 300387)



基于三角形模糊数的非线性T-S模糊系统的峰值点和分量半径优化

王宏志1, 陶玉杰1, 王贵君2*

(1. 通化师范学院 数学学院, 吉林 通化 134002; 2.天津师范大学 数学科学学院, 天津 300387)

摘要：单值模糊器是将高维空间中一个实值点映射成该空间上的一个单值模糊集,在构造非线性T-S模糊系统时不仅可克服输入变量的噪声问题,而且能减少模糊推理机设计中的计算量. 首先，基于分片线性函数和单值模糊器给出了非线性T-S模糊系统模型；并依据广义三角形的重心坐标公式，对等距剖分论域中的峰值点和分量半径等参数进行了优化；最后，通过模拟实例对系统进行了验证，得到优化后的非线性T-S模糊系统确实有更好的逼近效果.

关键词：分片线性函数;单值模糊器;非线性T-S模糊系统;峰值点;分量半径

WANG Hongzhi1, TAO Yujie1, WANG Guijun2

(1.SchoolofMathematics,TonghuaNormalUniversity,Tonghua134002,JilinProvince,China; 2.SchoolofMathematicsSciences,TianjinNormalUniversity,Tianjin300387,China)

0引言

模糊系统是一种基于知识或规则的系统,其核心是由若干条IF…THEN模糊规则所组成的知识库,其主要特性是通过多输入单输出映射将实值向量转化为实值标量,并获得这些映射的精确数学公式. 此外,模糊系统的主要贡献是为从知识库向非线性映射转换提供一套系统程序,使人们可将基于知识的系统通过传感器测量数据获取某些精确数学模型,进而将其应用于自动控制、信号处理、通信工程及空间技术等新型研究领域.1985年,TAKAGI-SUGENO(T-S)[1]基于非线性系统的输入输出数据首次提出T-S模糊系统模型.由于该系统的后件线性部分具有诸多随机调节参数,故T-S模糊系统比一般Mamdani模糊系统具有更好的逼近性能,且具有一定的灵活性和广泛性.1998年以来,文献[2-4]等成功将T-S模糊系统应用于系统建模和系统控制器设计等,并在一定范围内获得了T-S模糊系统构成逼近器的充分必要条件.这些结果为进一步探究模糊系统的逼近性和稳定性提供了帮助.

2000年,文献[5]通过剖分论域空间首次提出分片线性函数概念,并以此为桥梁证明了T-S模糊系统对L-可积函数具有泛逼近性；随之文献[6]研究了Mamdani模糊系统对一类p-可积函数的逼近问题.2007年,文献[7]通过选取前件模糊集为三角形模糊数引入了非线性T-S模糊系统模型,并讨论了该系统对连续函数的逼近性.近年来,文献[8]通过调节参数将Mamdani和T-S模糊系统混合建立了混合模糊系统,并基于叠加分层方法降低了混合系统内部的模糊规则总数,证明了分层后该系统仍具有逼近性能;文献[9]证明了在引入K-积分模下广义Mamdani模糊系统的泛逼近性.上述文献虽从理论上给出了模糊系统逼近性的严格证明,但并没有给出所涉及的分片线性函数的解析表达式,这不利于进一步研究广义模糊系统的逼近性或稳定性.

文献[10]首次在超平面下给出分片线性函数的解析表达式,并讨论了其对L-可积函数的逼近性.文献[11]基于分片线性函数重新构造了非齐次线性T-S模糊系统,并证明了规则后件线性部分所有参数选取非零常数时该系统对分片线性函数仍具有逼近性.文献[12]在Kp-积分模意义下研究了广义Mamdani模糊系统的逼近性和实现过程.2015年,文献[13]基于三角形模糊数和单值模糊器建立了非线性T-S模糊系统模型,并探究了该系统对一类p-可积函数的逼近性.本文在文献[10-13]基础上，通过优化峰值点和分量半径等参数来提高非线性T-S模糊系统的逼近性能,并通过模拟实例验证优化后的非线性T-S模糊系统的逼近效果.

1预备知识

自文献[5]提出分片线性函数概念以来，其应用范围日益凸显.本节首先给出分片线性函数、单值模糊器和高维三角形模糊数的定义.

定义1[5]设n元连续函数S:Rn→R,若满足如下条件:

①存在a>0,使S在广义正方体Δ(a)之外恒为0;

②存在若干n维多面体Δj⊂Δ(a),j=1,2,

(1)

∀x=(x1,x2,…,xn)∈Δj,j=1,2,…,Ns,

则称S为Rn上的分片线性函数,其中λij,βj均为可调节参数.

事实上,分片线性函数S不仅是一元分段线性函数在多元情况下的推广,而且是研究模糊系统逼近性理论的重要工具和手段.此外,它的一些优良性质(例如:紧集上取非零值,单边偏导数存在且有界,一致连续性等)也为进一步研究模糊系统的逼近性提供了便利.然而,文献[5]没能给出调节参数λij、βj和S的表达式,从而限制了分片线性函数S的广泛应用.

定理1[10-13]设f是给定紧集U⊂Rn上的Lebesgue可积函数,则存在a>0或广义正方体[-a,a]n⊇U,在[-a,a]n上分片线性函数S可使其按任意精度逼近f,其中，

S(x)=

(2)

其中线性部分系数行列式|Dj1|,|Dj2|,…,|Djn|,和|Dj|的含义参见文献[10-11].

2非线性T-S模糊系统

首先,基于文献[7,13]和上述三角形模糊数,给出模糊规则:

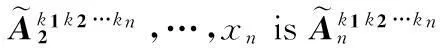
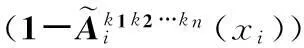
(3)

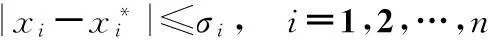
调控参数α∈(0,+∞).

文献[13]曾取非线性T-S模糊系统的系数为

对第j个区域Δji而言，可将系统(3)简化为

(4)

实际上,文献[13]仅证明了非线性T-S模糊系统(4)对所给分片线性函数乃至可积函数具有逼近性,并没有涉及逼近精度问题.

3参数优化

本节将对系统(3)的峰值点x*和分量半径σi重新进行选择和优化,使非线性T-S模糊系统Tm达到较好的逼近效果.

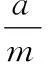
从图1和2容易看出，顶点分量坐标满足:

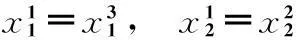
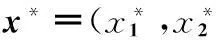
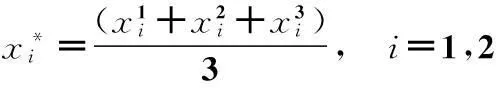
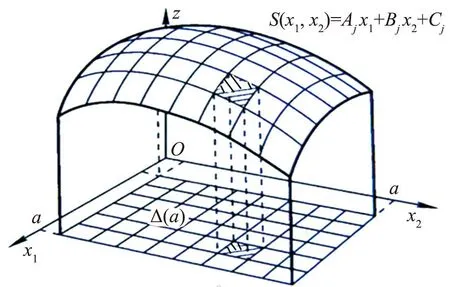
图1　n=2时PLF的局部平面示意图Fig.1　The local plane figure of PLF when n=2

图2　n=2时平面上剖分三角形Δji示意图Fig.2　Figure of subdivision triangle when n=2

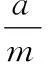
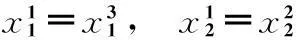
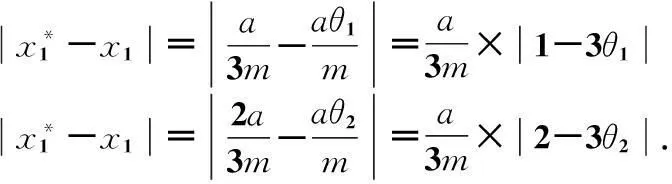
故有

因而,无论调节参数θ1与θ2怎样变化,恒有

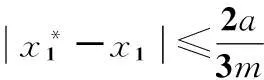
类似地,峰值点和动点的第2个分量也满足:

故无论哪种情况都有

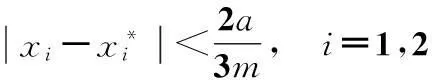
这意味着可优先选取分量参数σi为

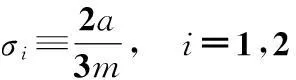
此时,若选取该系统所有调节参数为

(5)

则n=2时,非线性T-S模糊系统(3)可简化为

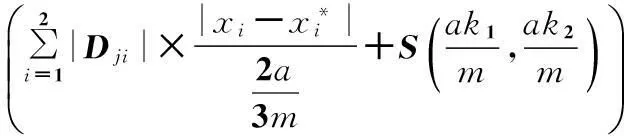
(6)

同理,对n维输入变量,若选取调节参数为

(7)

则非线性T-S模糊系统(3)可简化为

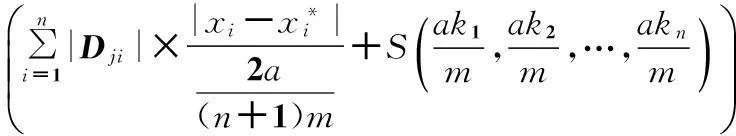
(8)

至此,获得了一般情况下非线性T-S模糊系统的解析式(式(8)).实际上,式(7)也可理解为参数优化的目标函数,这里不仅包括峰值点和分量半径等优化参数,而且还包含系统非线性部分的优化参数.这些参数在系统的逼近过程中均扮演重要角色.

4模拟实例

在低维空间(n=2)中进行模拟仿真,按式(6)给出如下实例:

设n=2,a=1,α=1,剖分数m=10,交互数c0=2,Δ(1)=[-1,1]×[-1,1].取二元函数为

按优化公式(5)或(7)选取优化分量半径

为直观起见,只对第1象限中单位正方形[0,1]×[0,1]实施等距剖分.故可将该正方形等分成10×10=100个边长为1/10的小正方形,再将每个小正方形沿对角线平分，可得200个小等腰直角三角形,按顺序将其记为Δji(j=1,2,…10;i=1,2,…,20),如图3所示.

图3　[0,1]×[0,1]上等距网格剖分图Fig.3　Subdivision figure of isometric grids in [0,1]×[0,1]

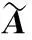
(9)

类似地,若在y轴闭区间[-1,1]上令

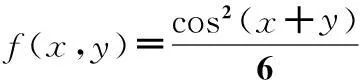
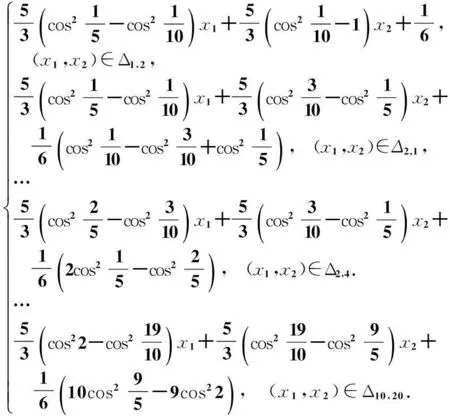
(10)

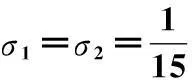
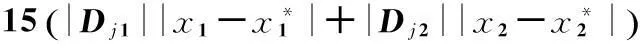
(11)

其中|Dj1|和|Dj2|如式(2)所示,其值随动点(x1,x2)的位置而变化[10].

f(0.15,0.08)≈0.158 004 374 8,

S(0.15,0.08)≈0.157 083 285 1.

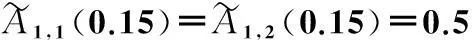
计算(顶点处f与S等值).

又因样本点(0.15,0.08)落在图3所示区域的Δ1,4内,故对应3个顶点坐标分别为

(0.1,0),(0.1,0.1),(0.2,0.1).

此时,按公式(5)可获得峰值点坐标x*和分量半径σi，分别为

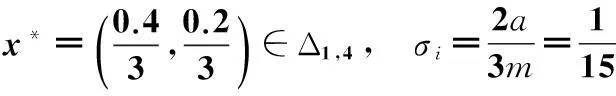
再由文献[10]及式(2)，获得二元分片线性函数S的系数行列式，分别为

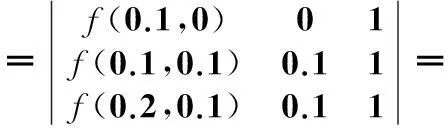
将样本点(0.15,0.08)代入式(11)得

T10(0.15,0.08)=0.157 687 053 9.

进而得到误差值为

|f(0.15,0.08)-S(0.15,0.08)|=

0.000 921 089 7,

|f(0.15,0.08)-T10(0.15,0.08)|=

0.000 317 320 9.

现在,在论域[0,1]×[0,1]内随机选取4个样本点

(0.04,0.06)∈Δ1,2,(0.05,0.12)∈Δ2,1,

(0.15,0.08)∈Δ1,4,(0.12,0.18)∈Δ2,4.

按公式(5)依次计算得对应峰值点,分别为

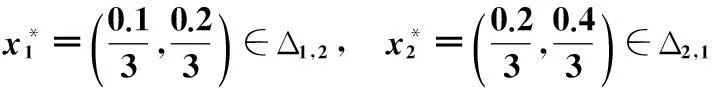
下面,随机选取上述4个样本点进行误差度量，通过多次平均值对比来分析系统的逼近效果.此外,本文优化选取的峰值点和分量半径更具一般性和系统性,其逼近精度随参数的优化而提高.表1为文献[13]和本文方法的输出值和误差值.

表1m=10时样本的输出值及误差

Table 1　Output values of the sample point and its serrors when m=10

5结论

为提高非线性T-S模糊系统的逼近性能,在等距剖分论域中对峰值点和分量半径重新进行优化选择,得到基于分片线性函数的非线性T-S模糊系统模型.结果表明,优化后的非线性T-S模糊系统具有更好的逼近精度.为进一步研究广义模糊系统的逼近性提供了新的方法和思路.当然,影响模糊系统逼近能力的调节参数或直接因素可能还有许多,有些影响甚至是潜在或间接的,有待进一步探究.

参考文献(References)：

[1]TAKAGI T,SUGENO M. Fuzzy identification of system and its applications to modeling and control[J].IEEE Transactions on Systems,Man and Cybern,1985,15:116-132.

[2]YING H,DING Y S,LI S K, et al. Comparison of necessary conditions for typical Takagi-Sugeno and Mamdani fuzzy systems as universal approximator[J].IEEE Transactions on Systems,Man and Cybernetics:A,1999,29(5):508-514.

[3]ZENG K,ZHANG N R,XU W L. A comparative study on sufficient conditions for Takagi-Sugeno fuzzy system as universal approximator[J].IEEE Transactions on Fuzzy Systems,2000,8(6):773-780.

[4]曾珂,张乃尧,徐文立.线性 T-S模糊系统作为通用逼近器的充分条件[J].自动化学报, 2001, 27(5):606-612.

ZENG Ke, ZHANG Naiyao, XU Wenli.Sufficient condition for linear T-S fuzzy systems universal approximator[J]. Acta Automatica Sinica, 2001,27(5): 606-612.

[5]刘普寅, 李洪兴. 广义模糊系统对于可积函数的逼近性[J].中国科学: E辑, 2000, 30 (5):413-423.

LIU Puyin, LI Hongxing. Approximation of generalized fuzzy systems to integrable functions[J].Science in China: Ser E, 2000, 30(5):413-423.

[6]LIU P Y,LI H X. Analyses forLp(μ)-norm approximation capability of the generalized Mamdani fuzzy systems[J].Information Sciences,2001,138(2): 195-210.

[7]刘福才,马丽叶,邵静,等.一类非线性T-S模糊系统的通用逼近性[J].自动化与仪器仪表,2007,129(1):8-15.

LIU Fucai,MA Liye,SHAO Jing, et al. Universal approximation of a class of nonlinear T-S fuzzy system [J]. Automation & Instrumentation, 2007,129(1):8-15.

[8]王贵君, 段晨霞. 广义分层混合模糊系统及其泛逼近性[J]. 控制理论与应用, 2012,29 (5):673-680.WANG Guijun,DUAN Chenxia.Generalized hierarchical hybrid fuzzy system and its universal approximation[J]. Control Theory and Application, 2012,29(5):673-680.

[9]王贵君, 李晓萍, 隋晓琳. 广义Mamdani模糊系统依K-积分模的泛逼近性及其实现过程[J].自动化学报, 2014, 40(1):143-148.

WANG Guijun, LI Xiaoping,SUI Xiaolin. Universal approximation and its realize process of generalized Mamdani fuzzy system in K-integral norms[J].Acta Automatica Sinica,2014,40(1):143-148.

[10]彭维玲.基于剖分模糊系统输入空间的多维分片线性函数的构造及逼近[J].系统科学与数学,2014,34(3):340-351.

PENG Weiling. Structure and approximation of a multidimensional piecewise linear function based on the input space of subdivision fuzzy systems[J]. System Science and Mathematical Sciences,2014,34(3): 340-351.

[11]王宏志,陶玉杰,王贵君.基于网格分片线性函数构造的非齐次线性T-S模糊系统的逼近性分析[J].系统科学与数学,2015,35(11):1276-1290.

WANG Hongzhi,TAO Yujie,WANG Guijun. Approximation analysis of nonhomogeneous linear T-S

fuzzy system based on grid piecewise linear function structure[J].System Science and Mathematical Sciences, 2015,35(11):1276-1290.

[12]陶玉杰,王宏志,王贵君.Kp-积分模意义下广义Mamdani模糊系统逼近性能及其实现[J].电子学报,2015,43(11):2284-2291.

TAO Yujie, WANG Hongzhi, WANG Guijun. Approximation ability and its realization of the generalized Mamdani fuzzy system in the sense ofKp-integral norm[J].Acta Electronica Sinica,2015,43(11):2284-2291.

[13]张国英,王贵君.基于三角形模糊化的非线性T-S模糊系统对p-可积函数的逼近性[J].浙江大学学报:理学版,2015,42(9):537-541.

ZHANG Guoying,WANG Guijun.Approximation capability of nonlinear T-S fuzzy system based on triangular fuzzifier top-integrable functions[J].Journal of Zhejiang University:Science Edition,2015,42(9):537-541.

[14]王立新.模糊系统与模糊控制教程[M].北京:清华大学出版社,2003.

WANG Lixin. A Course in Fuzzy Systems and Control[M]. Beijing:Tsinghua University Press,2003.

Optimizations of peak points and branch radius of nonlinear T-S fuzzy system based on triangular fuzzy numbers. Journal of Zhejiang University(Science Edition), 2016,43(3):264-270

Abstract:Single value fuzzifier is a mapping from a real value point to higher dimensional triangle fuzzy number in n-European space. It not only can overcome the noise of the input variables in constructing nonlinear T-S fuzzy system, but also can simplify the complicated calculation in the design of fuzzy inference engine. Firstly, a nonlinear T-S fuzzy system model is established based on the piecewise linear function and the single value fuzzifier. Secondly, the peak points and the branch radius in the equidistant subdivision universe are optimized by adopting the formula of barycenter of the generalized triangle. Finally, we verify that the optimized nonlinear T-S fuzzy system has good approximation effect by selecting the sample points.

Key Words:piecewise linear function; single value fuzzifier; nonlinear T-S fuzzy system; peak point; branch radius

中图分类号：O 174.4； O 159

文献标志码：A

文章编号：1008-9497(2016)03-264-07

作者简介：王宏志(1975-),ORCID：http://orcid.org/0000-0002-5417-6859,男,硕士,副教授,主要从事模糊系统分析研究，E-mail:whz-98@126.com.*通信作者，ORCID:http://orcid.org/0000-0002-2337-5951,E-mail:tjwgj@126.com.

基金项目：国家自然科学基金资助项目(61374009)；吉林省教育厅“十二五”科技项目(吉教科合字[2011]第456号).

收稿日期：2015-09-09.

DOI:10.3785/j.issn.1008-9497.2016.03.003