n次微分分次Poisson代数的泛包络代数

朱　卉, 吴学超, 陈淼森

(浙江师范大学 数学系, 浙江 金华 321004)



n次微分分次Poisson代数的泛包络代数

朱卉, 吴学超, 陈淼森*

(浙江师范大学 数学系, 浙江 金华 321004)

摘要：给出了n次微分分次Poisson代数的泛包络代数的定义及相关性质,同时给出了它的应用,即e是n次微分Z-分次Poisson代数范畴到微分Z-分次代数范畴的一个共变函子和(Ae)op=(Aop)e,其中A是任意的n次微分分次Poisson代数.

关键词：分次Poisson代数；泛包络代数; 微分分次代数映射; 微分分次李代数映射; 共变函子

0引言

Poisson代数可以简单地看成交换代数和李代数的结合. 近年来, Poisson代数在数学领域越来越受重视,并对其进行了研究和推广[1-9]. 吕家凤等[1]通过结合微分分次代数和分次Poisson代数定义了微分分次Poisson代数, 并给出了这类代数的基本性质. 同时, 详细研究了这类代数的泛包络代数及相关性质和应用. 注意在文献[1]中, 微分分次Poisson代数的Poisson括号是0次的, 而在微分分次李代数的定义中, 李括号是任意整数次. 因此吴学超等[9]给出了n次微分分次Poisson代数的定义. 受此启发, 本文定义了n次微分分次Poisson代数的泛包络代数, 并且给出了相关性质. 同时给出了其应用, 即e是n次微分 Z-分次Poisson代数范畴到微分 Z-分次代数范畴的一个共变函子和 (Ae)op=(Aop)e, 其中A是任意的n次微分分次Poisson代数.

本文的主要结果如下:

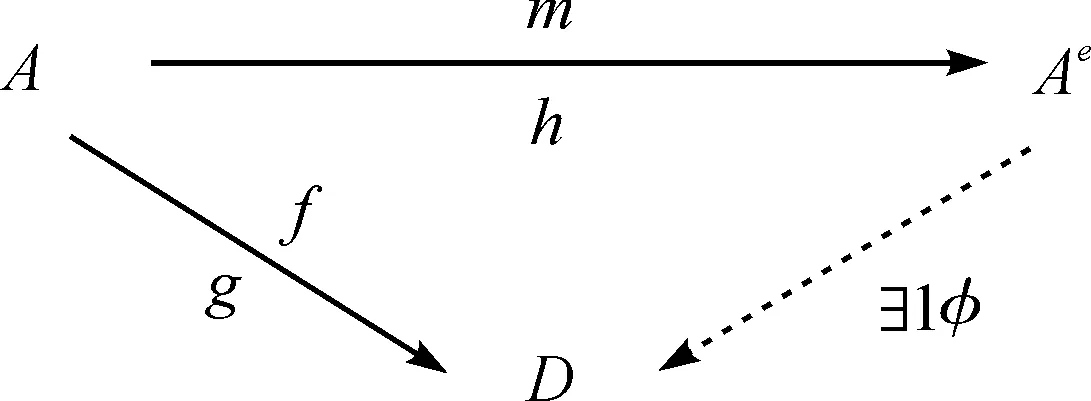
定理A(定理1)令(A,{,},d)是n次微分分次代数, 那么微分分次代数Ae是A的泛包络代数. 即(Ae,∂)有微分分次代数映射m:(A,d)→(Ae,∂)和微分分次李代数映射h:(A,{,},d)→(Ae,[,],∂), 次数为n, 满足下面的泛性质: 对于任意的微分分次代数(D,δ), 它包含微分分次代数映射f:(A,d)→(D,δ) 和微分分次李代数映射g:(A,{,},d)→(D,[,],δ), 次数为n, 满足

f({a,b})=g(a)f(b)-(-1)(|a|+n)|b|f(b)g(a),

g(ab)=f(a)g(b)+(-1)|a||b|f(b)g(a),

对于任意的齐次元a,b∈A, 都存在唯一的微分Z-分次代数映射φ:(Ae,∂)→(D,δ), 使得该图双交换, 即φm=f和φh=g.

定理B(定理1和3)令DGPA表示n次微分Z-分次Poisson代数范畴, DGA表示微分Z-分次代数范畴. 那么

(1)e:DGPA→DGA是一个共变函子;

(2) 对于任意的A∈DGPA，(Ae)op=(Aop)e.

1n次微分分次Poisson代数的泛包络代数

本节将给出n次微分分次Poisson代数的泛包络代数的定义及其相关性质.

定义1设(A,·)是Z-分次K-向量空间, 如果有K-齐次线性映射

{,}:A⊗A→A,|{,}|=n,

满足

(i)分次反对称性

{a,b}=-(-1)(|a|+n)(|b|+n){b,a};

(ii)分次Jacobi恒等式

{a,{b,c}}={{a,b},c}+(-1)(|a|+n)(|b|+n){b,{a,c}},

其中,a,b,c∈A为齐次元. 则称(A,{,})为n次分次李代数.

若在此基础上, 有K-线性映射d:A→A,|d|=1, 满足d2=0和

d({a,b})={d(a),b}+(-1)(|a|+n){a,d(b)},

则称(A,{,},d)为n次微分分次李代数.

定义2设(A,·)是Z-分次代数. 如果

(i) (A,{,})是n次分次李代数,

(ii)a·b=(-1)|a||b|b·a,

(iii){a,b·c}={a,b}·c+(-1)(|a|+n)|b|b·{a,c},

其中,a,b,c∈A为齐次元. 则称(A,·,{,})为n次分次Poisson代数.

若在此基础上, 有K-线性映射d:A→A,|d|=1满足d2=0和

(iv)d(a·b)=d(a)·b+(-1)|a|a·d(b),

(v)d({a,b})={d(a),b}+(-1)(|a|+n){a,d(b)}.

则称(A,·,{,},d)为n次微分分次Poisson代数.

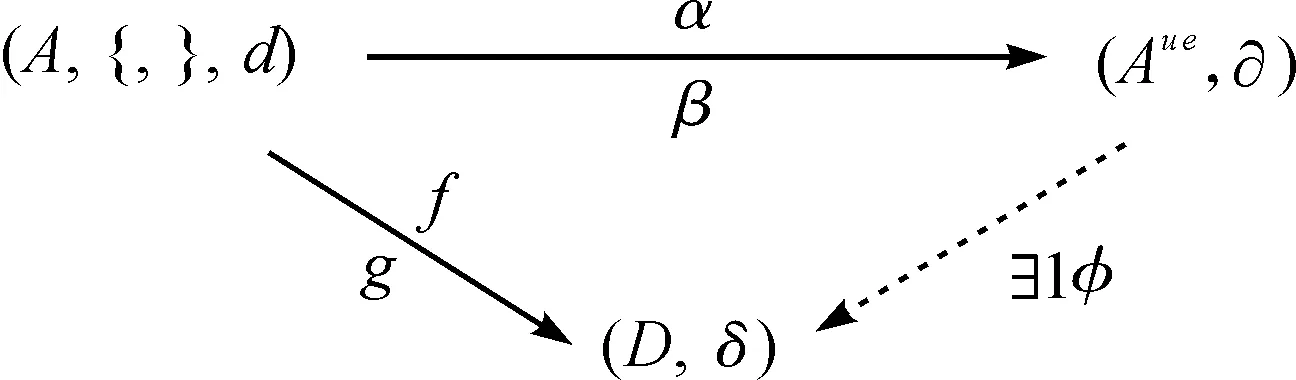
定义3令(A,{,},d)是n次微分Z-分次Poisson 代数, (Aue,∂)是微分Z-分次代数,(Aue,∂)为A的泛包络代数. 如果存在微分Z-分次代数映射α:(A,d)→(Aue,∂)和微分Z-分次李代数映射β:(A,{,},d)→(Aue,[,],∂), 次数为n, 满足

α({a,b})=β(a)α(b)-(-1)(|a|+n)|b|α(b)β(a),

β(ab)=α(a)β(b)+(-1)|a||b|α(b)β(a),.

对于任意的齐次元a,b∈A, 使得对于任意的微分Z-分次代数(D,δ), 它包含微分Z-分次代数映射f:(A,d)→(D,δ) 和微分Z-分次李代数映射g:(A,{,},d)→(D,[,],δ), 次数为n, 并且满足

f({a,b})=g(a)f(b)-(-1)(|a|+n)|b|f(b)g(a),

g(ab)=f(a)g(b)+(-1)|a||b|f(b)g(a),

对于任意的齐次元a,b∈A, 都存在唯一的微分Z-分次代数映射φ:(Aue,∂)→(D,δ), 使得该图双交换, 即φα=f和φβ=g.

命题1令(A,{,},d)是n次微分Z-分次Poisson代数, (Aue,∂)是它的泛包络代数, 那么在同构意义下(Aue,∂)是唯一的.

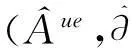
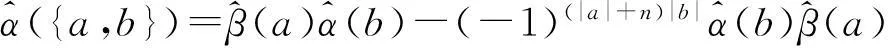
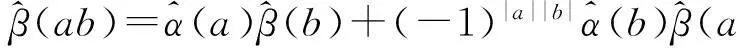
注意到,Aue和ue都是A的泛包络代数, 由定义1, 存在唯一的微分分次代数映射)和使得下面2个图双交换.

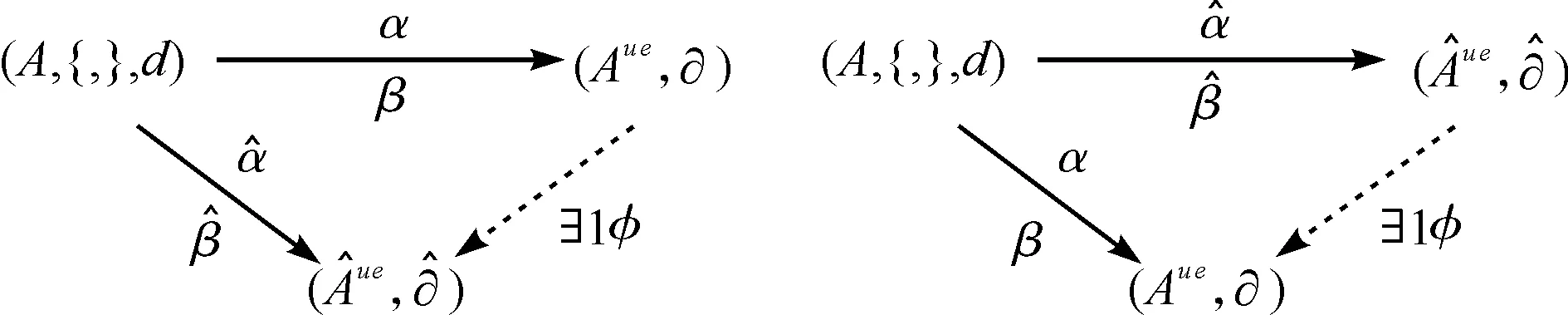
特别地, 有下面2个双交换图.

定理1令(A,{,},d)是n次微分Z-分次Poisson代数, 那么Ae是A的泛包络代数, 并且在同构意义下是唯一的. 其中Ae的定义如下:

mA:={ma|a∈A为齐次元},

hA:={ha|a∈A为齐次元},

m:A→mA且h:A→hA,

|ma|=|a|, |ha|=|a|+n,

Ae由mA和hA生成, 且生成关系为:

mab=mamb,

hab=mahb+(-1)|a||b|mbma,

m{a,b}=hamb-(-1)(|a|+n)|b|mbha,

h{a,b}=hahb-(-1)(|a|+n)(|b|+n)hbha,

m1=1,

其中a,b∈A为齐次元.

证明由命题1, 只需证Ae是A的泛包络代数. 首先, 已知Ae是微分分次代数. 注意到存在K-线性映射m:A→Ae把每个齐次元a∈A映射到ma和h:A→Ae把每个齐次元a∈A映射到ha, 这些就是需要的微分分次代数映射和微分分次李代数映射,次数为n,对于任意的齐次元a,b∈A，有

mab=mamb,

hab=mahb+(-1)|a||b|mbha,

m{a,b}=hamb-(-1)(|a|+n)|b|mbha,

h{a,b}=hahb-(-1)(|a|+n)(|b|+n)hbha,

m1=1,

∂(ma)=md(a),

∂(ha)=hd(a).

现令(D,δ)是任意的微分Z-分次代数, 其有微分Z-分次代数映射f:(A,d)→(D,δ)和微分Z-分次李代数映射g:(A,{,},d)→(D,[,],δ), 次数为n,对于任意的齐次元a,b∈A,满足

f({a,b})=g(a)f(b)-(-1)(|a|+n)|b|f(b)g(a),

g(ab)=f(a)g(b)+(-1)|a||b|f(b)g(a).

定义一个K-线性映射φ:(Ae,∂)→(D,δ), 其中,

φ(ma):=f(a),φ(ha):=g(a).

可以证明φ:Ae→D是Z-分次代数映射. 事实上, 对于任意的齐次元a,b∈A，只需证

φ(mab)=φ(mamb),

φ(hab)=φ(mahb+(-1)|a||b|mbha),

φ(m{a,b})=φ(hamb-(-1)(|a|+n)|b|mbha),

φ(h{a,b})=φ(hahb-(-1)(|a|+n)(|b|+n)hbha).

由前面的假设有f是微分Z-分次代数映射,g是微分Z-分次李代数映射, 次数为n, 且对于任意的齐次元a,b∈A,满足

f({a,b})=g(a)f(b)-(-1)(|a|+n)|b|f(b)g(a),

g(ab)=f(a)g(b)+(-1)|a||b|f(b)g(a).

可以证明上面式子成立. 进一步, 根据φ的构造, 知其是使得φm=f和φh=g成立的唯一映射. 同时, 也是微分分次代数映射. 因为, 对于任意的齐次元a∈A,有φ(∂(ma))=φ(md(a))=f(d(a))=δ(f(a))=δ(φ(ma))

和φ(∂(ha))=φ(hd(a))=g(d(a))=δ(g(a))=δ(φ(ha)).

注记1从现在开始, 由定理1, 用Ae来表示n次微分分次Poisson代数A的泛包络代数.

2应用

作为n次微分分次Poisson代数的泛包络代数的泛性质的应用, 本文将证明e是n次微分Z-分次Poisson 代数范畴到微分Z-分次代数范畴的一个共变函子和 (Ae)op=(Aop)e, 其中，A是任意的n次微分分次Poisson代数.

令DGPA为n次微分Z-分次Poisson代数范畴, DGA为微分Z-分次代数范畴.

2.1DGPA→DGA是一个共变函子

定理2e:DGPA→DGA是一个共变函子.

证明对于任意的A∈DGPA, 定义e(A):=Ae. 已知Ae∈DGA. 对于任意DGPA中的微分分次Poisson代数映射 f:A→B, 注意到mBf:A→Be是微分分次代数映射, hBf:A→Be是微分分次李代数映射, 次数为n, 且满足

mBf({a,b})=hBf(a)mBf(b)-

(-1)(|a|+n)|b|mBf(b)hBf(a),

hBf(ab)=mBf(a)hBf(b)+

(-1)|a||b|mBf(b)hBf(a).

由定理1, 已知Ae是A的泛包络代数, 那么存在唯一的微分分次代数映射fe:Ae→Be, 使得下图双交换. 然后定义e(f):=fe. 进一步,对于任意的A∈DGPA,有e(1A)=1Ae.

类似地,对任意的微分分次Poisson代数映射f:A→B和g:B→C, 分别选取A, B和C的泛包络代数Ae, Be和Ce, 则有下面的双交换图.

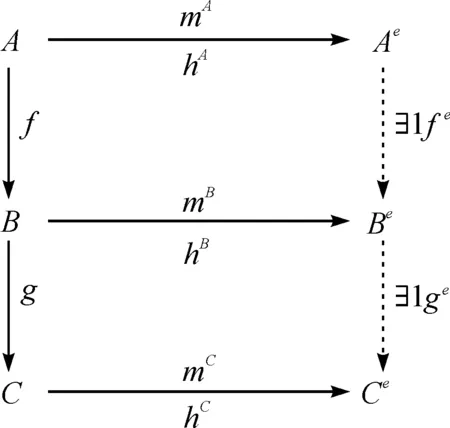
因此有

e(gf)=gefe=e(g)e(f).

得到e:DGPA→DGA是一个共变函子.

2.2(Ae)op=(Aop)e

先给出下面的引理.

引理1令(A,·,{,},d)是任意的n次微分分次Poisson代数, 那么(Aop,·op,{,}op,dop)也是n次微分分次Poisson代数, 其中,对于任意的齐次元a,b∈A,

a·opb:=(-1)|a||b|b·a=a·b,

dop:=d,

{a,b}op:=(-1)(|a|+n)(|b|+n){b,a}=-{a,b}.

引理2令A,B,C∈DGPA, 有下面的结论:

(1) 如果f:A→B是微分分次代数映射, 那么fop:Aop→Bop也是微分分次代数映射, 其中fop(a):=f(a); 如果f:A→B是微分分次李代数映射, 次数为n, 那么fop:Aop→Bop也是微分分次李代数映射, 次数为n, 其中fop(a):=f(a). 因此, 如果f是微分分次Poisson代数映射, 那么fop也是.

(2)(Aop)op=A和(fop)op=f, 其中f是DGPA中任意的微分分次Poisson代数映射.

(3)如果f:A→B和g:B→C是2个微分分次代数映射, 那么(gf)op=gopfop:Aop→Cop也是微分分次代数映射; 如果f:A→B和g:B→C是2个微分分次李代数映射, 次数为n, 那么(gf)op=gopfop:Aop→Cop也是微分分次李代数映射, 次数为n.

(4)Γ是DGPA的交换图,⟺Γop是DGPA的交换图, 其中Γop是用映射fop替代f得到.

证明只需证(1), 因为(2)～(4)可以根据“op”的定义直接得到. 如果A,B∈DGPA且f:A→B是微分分次代数映射, 那么对于任意的齐次元a,b∈A, 有f(ab)=f(a)f(b),fdA=dBf. 因此，由引理1,对于任意的齐次元x,y∈Aop, 有

fop(xy)=f(xy)=f(x)f(y)=fop(x)fop(y)，

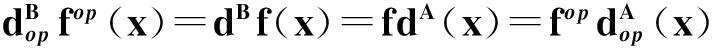
是微分分次代数映射. 如果f:A→B是微分分次李代数映射, 次数为n, 那么对于任意的齐次元a,b∈A, 有f({a,b}A)={f(a),f(b)}B,fdA=dBf. 由引理1,对于任意的齐次元x,y∈Aop,有

fop({x,y}Aop)=-f{x,y}A=-{f(x),f(y)}B=

{fop(x),fop(y)}Bop，

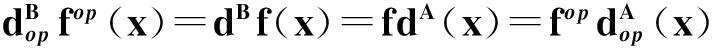
定理3令A∈DGPA, 那么(Aop)e=(Ae)op.

证明已知存在K-线性映射m,h:A→Ae满足m是微分分次代数映射,h是微分分次李代数映射, 次数为n, 对于任意的齐次元a,b∈A, 有

hab=mahb+(-1)|a||b|mbha,

(1)

m{a,b}=hamb-(-1)(|a|+n)|b|mbha.

(2)

由定义1和引理2, 有K-线性映射mop,hop:Aop→(Ae)op满足mop是微分分次代数映射,hop是微分分次李代数映射, 次数为n.

进一步, 对于任意的齐次元a,b∈Aop，要证明

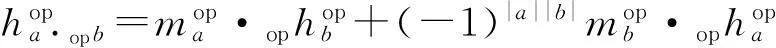
(3)

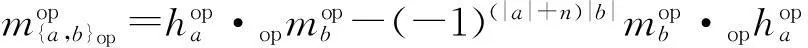
(4)

需先证明式(3).

由式(2), 对于任意的齐次元a,b∈A,有

hbma-(-1)(|b|+n)|a|mahb=m{b,a},

(5)

hamb-(-1)(|a|+n)|b|mbha=m{a,b}.

(6)

根据式(1), (5)和(6), 对于任意的齐次元a,b∈A, 得到

(-1)n|b|hamb+(-1)|a||b|+n|a|hbma=hab.

(7)

式(3)可以由式(7)两边进行“op”得到. 对于任意的齐次元a,b∈A, 式(4)等价于

-m{a,b}=(-1)(|a|+n)|b|mbha-hamb,

(8)

式(8)同式(2).

现令Dop是任意的微分Z-分次代数, 它包含微分Z-分次代数映射fop:Aop→Dop和微分Z-分次李代数映射gop:Aop→Dop, 次数为n, 对于任意的齐次元a,b∈Aop, 满足

fop({a,b}op)=gop(a)·opfop(b)-

(-1)(|a|+n)|b|fop(b)·opgop(a),

gop(a·opb)=fop(a)·opgop(b)+

(-1)|a||b|fop(b)·opgop(a).

与上面的证明类似, 有微分分次代数映射f:A→D和微分分次李代数映射g:A→D, 次数为n, 对于任意的齐次元a,b∈A, 满足

f({a,b})=g(a)f(b)-(-1)(|a|+n)|b|f(b)g(a),

g(ab)=f(a)g(b)+(-1)|a||b|f(b)g(a).

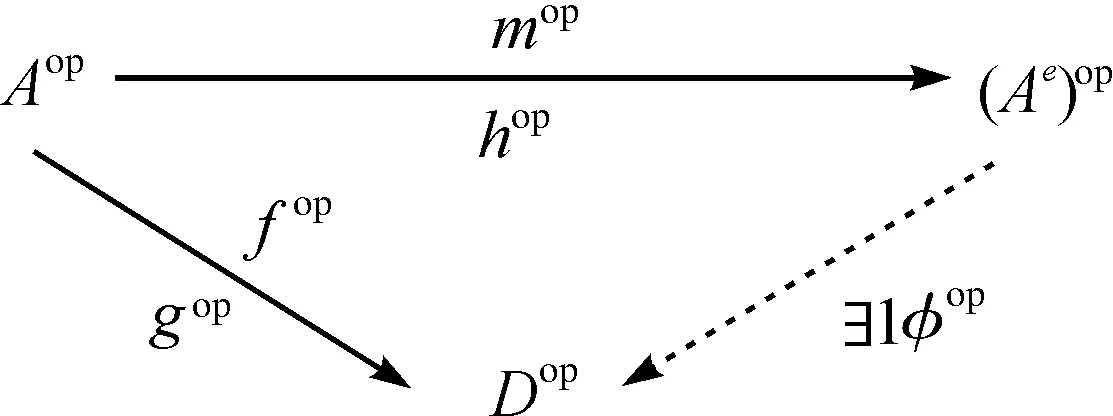
注意到Ae是A的泛包络代数, 存在唯一的微分分次代数映射φ, 使得图双交换. 又由引理2, 存在唯一的微分分次代数映射φop, 使得图双交换. 因此, 有(Aop)e=(Ae)op.

参考文献(References)：

[1]LYU J F, WANG X, ZHUANG G. Universal enveloping algebras of differential graded Poisson algebras[J]. Eprint Arxiv, 2014, arXiv:1403.3130.2014.

[2]ROITMAN M. Universal enveloping conformal algebras[J]. Selecta Mathematica,2000,6(3)：319-345.

[3]CATTANEO A S, FIORENZA D, LONGONI R. Graded Poisson algebras[J]. Encyclopedia of Mathematical Physics,2006(2):560-567.

[4]OH S Q. Poisson enveloping algebras[J]. Communications in Algebra,1999,27:2181-2186.

[5]OH S Q, PARK C G, SHIN Y Y. A Poincaré-Birkhoff-Witt theorem for Poisson enveloping algebras[J]. Communications in Algebra,2002,30(10):4867-4887.

[6]BAO Y H, LI H. Notes on Poisson enveloping algebras[J]. Journal of Anhui University:Natural Science Edition,2013,37(1):23-27.

[7]UMIRBAEV U. Universal enveloping algebras and universal derivations of Poisson algebras[J]. Journal of Algebra,2012,354(1):77-94.

[8]BECK K A, SATHER-WAGSTAFF S. A somewhat gentle introduction to differential graded commutative algebra[C]// Connections Between Algebra, Combiatorics, and Geometry Spinger Proceedings in Mathematics and Statistics,2014,76:3-99.http://arxiv.org/abs/1307.0369.

[9]吴学超，朱卉，陈淼森.n次微分分次Poisson代数的张量积[J]. 浙江大学学报：理学版,2015,42(4):391-395.

WU Xuechao, ZHU Hui, CHEN Miaosen. The tensor product ofn-differential graded Poisson algebras[J]. Journal of Zhejiang University:Science Edition,2015,42(4):391-395.

ZHU Hui, WU Xuechao, CHEN Miaosen
(DepartmentofMathematics,ZhejiangNormalUniversity,Jinhua321004,ZhejiangProvince,China)
The universal enveloping algebras ofn-differential graded Poisson algebras. Journal of Zhejiang University(Science Edition), 2016,43(3):253-256

Abstract:In order to study more extensively about Poisson algebras, this paper presents the definition and some properties of universal enveloping algebras of n-differential graded Poisson algebras and proves that universal enveloping algebras of n-differential graded Poisson algebras are differential graded algebras. During the study of the universal enveloping algebras of n-differential graded Poisson algebras, we find many interesting results. As applications, we prove that e is a covariant functor from the category of n-differential Z-graded Poisson algebras to the category of differential Z-graded algebras and (Ae)op=(Aop)e, for any n-differential graded Poisson algebras A.

Key Words:graded Poisson algebras; universal enveloping algebras; differential graded algebra map; differential graded Lie algebra map; covariant functor

中图分类号：O 154.2

文献标志码：A

文章编号：1008-9497(2016)03-253-04

作者简介：朱卉(1991-),ORCID:http://orcid.org/0000-0001-9888-6740,女,硕士研究生,主要从事代数学研究.*通信作者，E-mail：mschen@zjnu.cn.

收稿日期：2015-12-21.

DOI:10.3785/j.issn.1008-9497.2016.03.001