《等腰三角形》教学实录与评析

蒙榜中 周忠

一、创设情境，引出课题

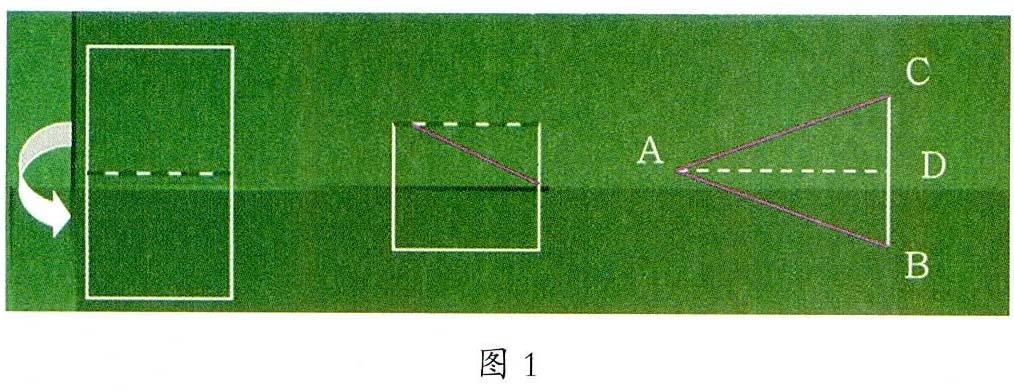
活动1.教师剪纸，请学生观察图形（见图1）。教师把一张长方形的纸按图中虚线对折，然后用剪刀沿着实线剪开，留下三角形部分，再把它展开。

师：这是一个什么三角形？为什么？

生：这是等腰三角形，因为AB=AC.

师：你怎么知道AB和AC的长度相等呢？

生1：因为△ABD≌△ACD，AB与AC是对应边，所以AB=AC.

生2：因为AB与AC重合，所以它们的长度相等。

师：很好，请你们观察图形，折痕左右两边重合吗？等腰三角形是轴对称图形吗？

生：折痕左右两边重合，等腰三角形是轴对称图形。

师：你认识等腰三角形的腰、底边、顶角、底角吗？（展示教具，学生回答）虽然前面我们学习了等腰三角形的知识，但是有关它的性质、判定都没有涉及，这节课我们进一步学习等腰三角形。（板书：等腰三角形）

【评析】教学伊始，执教老师就创设情境，让学生观察老师的操作过程，得到研究对象——等腰三角形后，再请学生观察图形，回顾等腰三角形的相关概念如腰、底边、顶角、底角以及等腰三角形的对称性，引导学生学会观察并发现问题，让学生感受到重合即相等，为后面探究等腰三角形的性质奠定基础。

二、实践操作，发现性质

活动2：请学生用纸剪出一个等腰三角形。

师：仔细观察剪好的等腰三角形，你发现这个等腰三角形有哪些线段相等？哪些角相等？

生独立观察，指出等腰三角形中相等的线段和相等的角。

师：请同桌之间互相交换等腰三角形，再次观察，你发现等腰三角形有哪些线段相等？哪些角相等？说一说这些线段和角在等腰三角形中的名称。

生1：等腰三角形的两条腰相等。

生2：等腰三角形的两个底角相等。

教师板书，等腰三角形的性质1：等腰三角形的两个底角相等。简写为：等边对等角。

【评析】教师让学生通过操作、观察、发现、归纳，得出等腰三角形的两个底角相等这一性质，体现了学生的学习主体地位。这样做有利于学生从研究一个等腰三角形拓展到其他等腰三角形，由特殊到一般，从而发现等腰三角形的特征，归纳得出等腰三角形的性质1：等腰三角形的两个底角相等。

三、关注折痕，引出三线

教师在剪好的等腰三角形的折痕上画一条虚线（见图2），请学生仔细观察等腰三角形，注意折痕，并思考还能发现哪些线段相等？哪些角相等？

学生先观察图形，然后分小组讨论，最后展示分享结果。

生1：BD=CD.

生2：∠BAD=∠CAD.

生3：∠ADB=∠ADC.

师：假如BD=CD，那么AD与BC是什么关系呢？

生：AD是BC的中线。

师补充说明AD是等腰三角形底边BC的中线。

师：刚才有位同学说∠BAD=∠CAD，想一想，AD与∠BAC是什么关系？

生：AD是∠BAC的平分线。

师补充说明AD是等腰三角形顶角∠BAC的平分线。

师：请同学们思考∠ADB=∠ADC等于多少度？为什么？

生：∠ADB=∠ADC=90°，因为∠ADB+∠ADC=180°，∠ADB=∠ADC，所以∠ADB=∠ADC=90°.

师：AD与BC是什么关系？

生4：AD是BC边上的高。

生5：AD是等腰三角形底边BC上的高。

师：我们在表达线段的关系时要准确、完整，综上所述，AD是等腰三角形的什么？

生：AD是等腰三角形底边BC上的中线，是等腰三角形顶角∠BAC的平分线，是等腰三角形底边BC上的高。

【评析】教师让学生观察、发现，然后准确全面地归纳出等腰三角形的性质2：等腰三角形的顶角平分线、底边上的高、底边上的中线互相重合，简称“三线合一”。

四、推理证明，验证性质

题目：利用实验操作的方法，我们发现并概括得出等腰三角形的性质1：等腰三角形的两个底角相等。你能运用逻辑推理来证明这个命题吗？

生：根据命题，我们可以画出图形（见图3），写出已知、求证。

已知：在△ABC中，AB=AC.

求证：∠B=∠C

教师引导学生思考：结合所画的图形，你认为证明两个底角相等的思路是什么？如何在一个等腰三角形中构造出两个全等三角形？从剪图、折纸的过程中你能够获得什么启发？

生1：我认为可以画一条辅助线（见图4），把三角形△ABC分为两个三角形，通过证明两个三角形全等，可以得到∠B=∠C.

证明：作底边BC的中线AD，在△ABD与△ACD中，

因为：AB=AC

BD=CD

AD=AD

所以：△ABD≌△ACD（SSS）

∠B=∠C

师：这位同学使用的方法很正确，思路清晰，板书规范。请你们再想一想，还有别的证明方法吗？请结合图形说明你的思路。

生2：我的思路是作底边BC上的高AD，然后运用“HL”证明直角三角形ADB与直角三角形ADC全等，从而得到∠B=∠C.

生3：我的思路是作顶角∠BAC的平分线AD，然后运用“SAS”证明△ABD与△ACD全等，从而得到∠B=∠C.

师：这3位同学的证明思路、推理方法都是对的。通过学习等腰三角形的性质，我们又掌握了证明两个角相等、两条线段相等以及线段互相垂直关系的新方法。

【评析】教师让学生体验证明两个角相等到证明两个三角形全等的过程，了解添加辅助线与解决问题思路的相关性，进一步理解等腰三角形的性质及意义——它既是三角形全等知识的运用和延续，又是证明两个角相等、两条线段相等、线段垂直关系的更为简捷的途径和方法。

五、解读性质，注重表达

师：等腰三角形性质2的“三线合一”是指什么？对此，我们可以将其分解为下面3个结论：①等腰三角形的顶角平分线也是底边上的中线和高；②等腰三角形底边上的中线也是底边上的高和顶角平分线；③等腰三角形底边上的高也是顶角平分线和底边上的中线。

师： ∵AB=AC，∠BAD=∠CAD

∴BD=CD，AD⊥BC

请同学们用符号语言表达第②、③两个结论。

生1： ∵AB=AC，BD=CD

∴AD⊥BC，∠BAD=∠CAD

生2： ∵AB=AC，AD⊥BC

∴∠BAD=∠CAD，BD=CD

【评析】教师让学生在反复比较的过程中概括得出等腰三角形共同的、本质的特征，进一步培养了学生运用数学语言符号进行表达的能力，使学生真正理解“三线合一”的含义。

六、学以致用，巩固新知

（一）填空。

1.如图5，在△ABC中，AB=AC，∠A=36°，则

∠B= .

2.如图6，在△ABC中，AB=AC，∠B=30°，则

∠A= .

（二）自制水平仪。教师选用教学时用的等腰三角板一个，铅垂一个，1米长的细绳一根，展示：用水平仪测量讲台是否处于水平状态，请学生说明测量时用到了什么数学知识？学生回答，相互补充，并说明理由。

【评析】教师设计角度计算题，学生需要综合运用等腰三角形、三角形的内角和等知识解决问题，这样做有利于学生进一步掌握等腰三角形的性质1，同时引导学生将与角有关的知识系统化，有助于学生优化知识结构。此外，教师设计活动操作题，能够让学生体会到数学知识在生活中的实际应用，体现了学习数学的价值。

七、学会总结，提高更快

师：我们是如何探究等腰三角形的性质呢？

生：动手操作，通过观察、发现、归纳性质，最后证明性质。

师：你学到了哪些证明线段相等或角相等的方法？

生1：在同一个三角形中，相等的边所对应的角相等。

生2：根据“三线合一”的性质，等腰三角形底边上的高（或顶角平分线）也是底边上的中线，从而有线段相等。

生3：根据“三线合一”的性质，等腰三角形底边上的高（或底边上的中线）也是顶角平分线，从而有角相等。

【评析】通过小结，学生掌握了本节课所学的核心知识——等腰三角形的性质及应用。

【总评】这节课，学生在学习了三角形的基本概念、全等三角形和轴对称知识的基础上，进一步研究特殊的三角形——等腰三角形。学习目标是：探索并证明等腰三角形的两个性质；能够利用等腰三角形的性质证明两个角相等或两条线段相等；结合等腰三角形性质的探索与证明过程，体会轴对称在研究几何问题中的作用。

为了达成教学目标，教师设计了“情境导入—引出概念—归纳性质—验证性质—实际应用”等环节，并逐一展开教学，体现了以下几个特点。第一，教学设计层次分明，以活动为主线，层层递进，教学过程将观察发现、归纳总结与证明性质有机地结合起来，让学生经历了知识的应用过程。第二，教学突出了数学思想，数学思想方法大多隐藏在知识的形成过程中，对新知的形成和发展起着重要的作用。比如，等腰三角形性质的证明过程是将欲证明相等的两个角（或两条线段）置于两个全等三角形之中，这是证明两个角相等或两条线段相等的基本方法，学生动手操作，对折长方形纸片，留下的折痕把等腰三角形转化为两个三角形，而对等腰三角形性质的探索与证明体现了转化的数学思想。第三，让学生成为学习的主人。前苏联教育家苏霍姆林斯基指出：“在人的心灵深处，都有一种根深蒂固的需要，就是希望自己是一个发现者、探索者。”在探索等腰三角形的性质时，教师引导学生利用轴对称知识进行证明，借助轴对称发现等腰三角形的性质，获得了添加辅助线证明性质的方法。为了让学生体验操作过程，教师让学生动手操作、观察发现、合作交流、验证探究、实际应用，为学生提供了充分的探索机会，帮助他们获得数学知识的经验，培养了学生观察问题、思考问题、解决问题的能力，增强了学好数学的信心。第四，教师注重学用结合，让学生体会到了数学与生活的紧密联系，如自制水平仪的活动，使学生意识到数学就在身边，体现了数学的实用价值，从而激发了学生学习数学的热情。

（注：该课荣获2015南宁市初中数学课堂教学优质课比赛一等奖。）

（责编 欧孔群）