带退货的周期车辆路径问题的C—W节约算法
2016-05-31窦冰洁张丽华赵丽娜孙蕊
窦冰洁 张丽华 赵丽娜 孙蕊
摘 要:文章用MATLAB代码给出了一个改进的C-W节约算法来求解带退货的周期车辆路径问题,目标是最小化周期内总的行驶费用和总的启动费用之和,并举例对算法进行了说明。
关键词:运筹学;周期车辆路径问题;C-W节约算法
中图分类号:U116.2 文献标识码:A
Abstract: In this paper, an improved C-W saving algorithm is given by MATLAB codes to solve the periodic vehicle routing problem with backhauls, aiming to minimize the sum of the total travel expenses and the total startup cost over the planning horizon, an example is gives to illustrate the algorithm.
Key words: operations research; periodic vehicle routing problem; C-W saving algorithm
0 引 言
周期车辆路径问题(Period Vehicle Routing Problem, PVRP)是车辆路径问题(Vehicle Routing Problem, VRP)的一个重要的分支,最早由Beltrami和Bodin[1]于1974年提出,是VRP在时间上的扩展,而由于企业很多计划都是按一定的周期来制定的,所以PVRP有着很强的实用价值,因此到目前为止国内外对其进行的研究已有很多成果:Ann和Jill[2]对国外从1974到2012年这方面的文献以及2013年的部分文献进行了详细综述,之后又有10多篇文献[3-13]对PVRP进行了研究。国内学者在VRP领域进行了大量的研究,但目前对PVRP方面的研究还比较少:姜贵山[14]设计了改进的引导邻域搜索算法、蔡婉君等[15]给出了改进的蚁群算法来求解PVRP。以上这些文献可分为两种类型:(1)只送货的PVRP问题;(2)带取送货(pickup and delivering)的PVRP。其中只有文献[10]和[16]是研究类型(2)的,然而近年来,保障商品质量、上架及时和退货服务成为电商及大型连锁超市应对激烈的市场竞争的关键所在,而在这一过程中物流配送是核心环节,因此受到了高度的关注。另外,不同种类货物的销售多受地域影响,以及消费者维权意识的增强,使得超市间货物调换和产品退回事件趋于普遍,这就要求发展逆向物流配送系统,因此,本文研究了一个带退货的PVRP,该问题隶属于类型(2)中带同时取送货的PVRP,而且要求每个客户在其被服务的各个时间段里取货和送货任务都由一辆车来完成,这与文献[10]和[16]研究的问题都有所不同。
1 问题描述及数学模型
1.1 问题描述
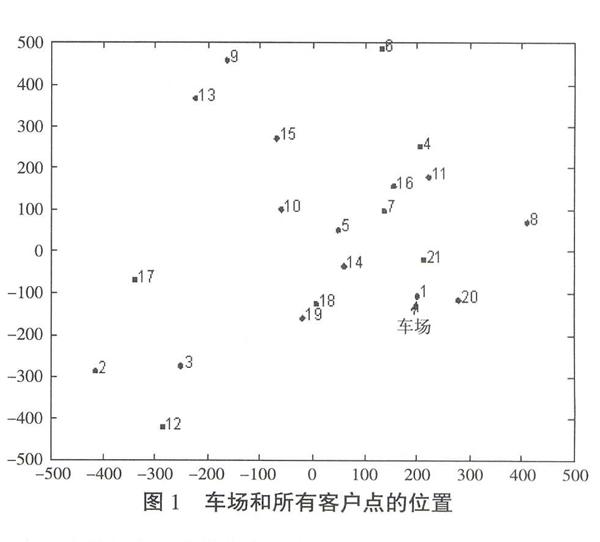
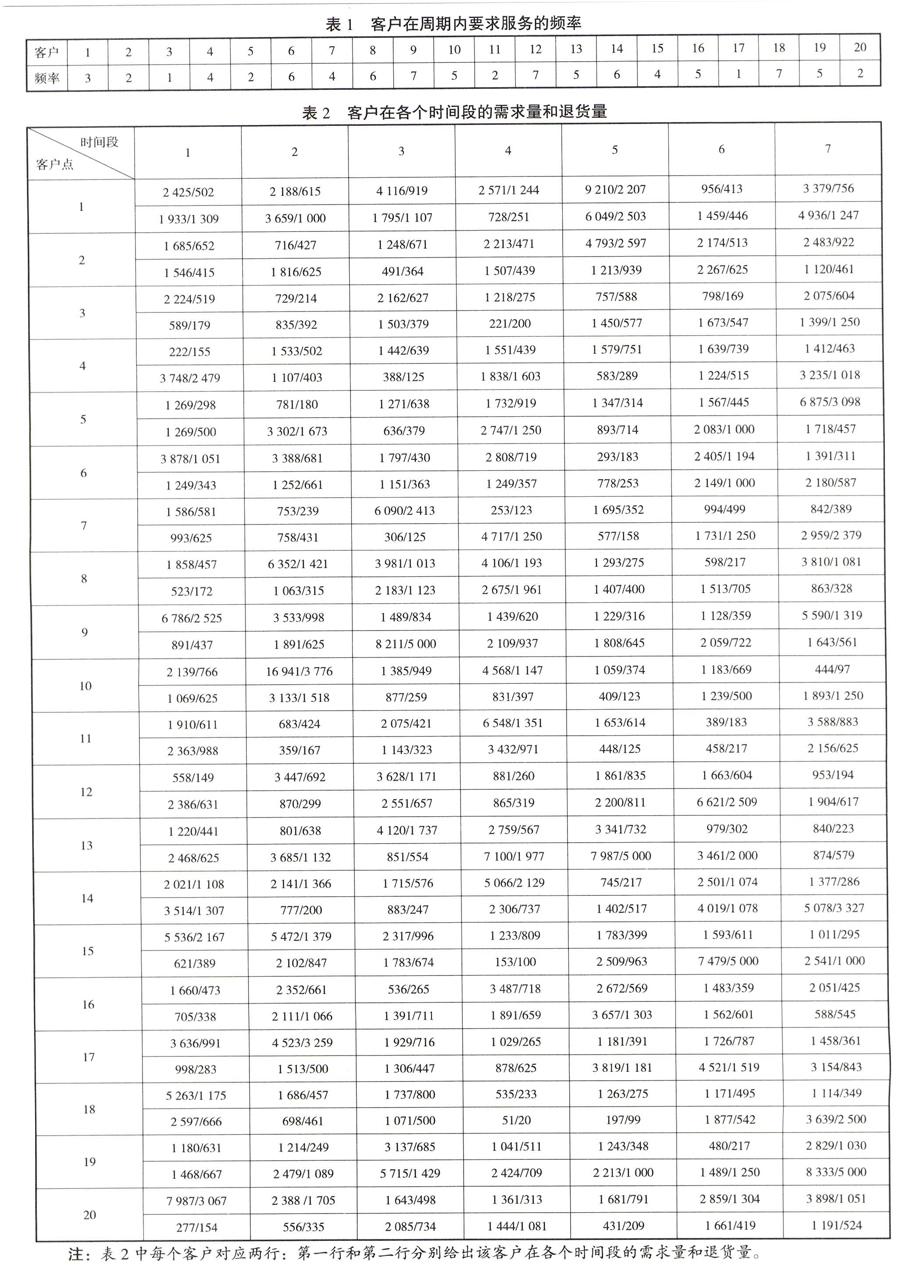
在一个区域内有一个配送站点(车场),m个顾客,一个周期中有T个时间段,顾客ll=1,2,…,m在周期内要求的服务次数(以下简称频率)为f0 当各个顾客的退货量都是零时上述问题就是传统的PVRP,因此传统的PVRP是本文所讨论问题时的子问题。因PVRP是NP-hard的,所以本文的问题也是NP-hard的。 1.2 数学模型 令N为顾客点集合,N=1,2,3,…,m,0表示车场;A为弧的集合,a为连接客户点i和j的弧;d和c分别表示i与j之间距离和单位距离的运输费用(当i=j时,d=0, c=0);K表示所有车辆集合;Q和C分别表示每辆车的车载限制和一次性启动费用;在周期为T个时间段计划中,f表示客户i要求的频率,分别表示客户i在第t个时间段t∈T的需求量与退货量。模型中决策变量为:w表示第t天弧a上的车载量。 式(1)的第一项为总的行驶费用,第二项为总的启动费用;式(2)保证对每一个客户点总访问次数等于其要求频率;式(3)表示被一辆车依次服务的两个客户点必须被安排在同一个时间段;式(4)为流平衡约束:在第tt=1,…,T个时间段进入某点的车辆数等于从此点出去的车辆数;式(5)表示分配到每一个时间段的所有客户点在该时间段都被访问到;式(6)为子回路消去约束;式(7)表示一辆车在一个时间段内最多只被用一次;式(8)至式(10)表示车辆在行驶过程中的车容量约束;式(11)至式(13)定义变量的取值范围。 2 问题求解 姜贵山[20]设计改进的引导邻域搜索算法中,提出应用C-W节约算法构建PVRP的初始可行解。本文对此算法做出进一步改进,得到解决本问题的改进C-W 节约算法,下面用Matlab代码给出该算法。 function [solution, Customers_just_information]=Modified_CW_SAT,m,f,M,p,q,Q本函数Modified_CW_SA为求解带退货的周期车辆路径问题的修改C-W节约算法。 T,m,Q: 分别存储周期长度、客户数量、车辆容量;f: 是一个1×m矩阵,存储所有客户的频率;M: 是一个m×m矩阵, 存储所有客户间的节约值;p,q: 都是T×m矩阵, 分别存储每个时间段所有客户的需求量和退货量;solution:是一个T行m+1列的元胞数组,各行第一个元素存储该行对应时间段路径总数,其余元素分别存储该行对应时间段里的各条路径; Customers_just_information: 是一个m行2列的元胞数组, 其第i行第1个元素Customers_just_informationi,1存储一个1×T矩阵,该矩阵的第j个元素Customers_just_informationi,1j=0或1,前者和后者分别表示第i个客户在第j个时间段没有被服务和已经被服务,Customers_just_information的第i行第2个元素Customers_just_informationi,2存储一个T×3 矩阵,该矩阵的第t行第1-3个元素Customers_just_informationi,2t,s,s=1,2,3依次存储第i个客户在第t个时间段所在的路径(在第k条路径上就存k)、在该路径上的位置(是该路径上第u个客户点就存u)、该路径的长度。
Customers_just_information=cellm,2; solution=cellT,m+1;
for k=1:m
Customers_just_informationk,1=zeros1,T; Customers_just_informationk,2=zerosT,3;
end
for v=1:T
solutionv,1= 0;
end
temp_M=M:; hs,wz=sorttemp_M, 1,'descend'; temp=findM~=0,1;
while~isempty(temp)
for s=1:m^2
x,y=ind2subsizeM,wzs; wzs对应的客户点x,y;nx,ny:客户点x,y当前已被服务的次数。
nx=sum(Customers_just_informationx,1(:)); ny=sum(Customers_just_informationy,1(:));
if nx==fx&& ny==fy
Mx,y=0; temp_M=M(:); hs,wz=sorttemp_M, 1,'descend'; temp=findM~=0,1; break
end
if nx==fx&& ny left_ny=fy-ny; 客户点y的剩余被服务次数 [newCustomers_just_information, newsolution]=Joint_point_to_endpoint (Customers_just_information, solution, x, y, left_ny, p, q, Q); 调用函数Joint_point_to_endpoint来处理x为端点而y未被服务的那些时间段函数Joint_point_to_endpoint先在所有的时间段里寻找未完成路径中以客户点x为端点且在该时间段里客户点y未被服务的时间段,之后判别在这些时间段里将客户点y安排在客户点x之前或之后是否可行且客户点y被安排的次数不超过其剩余被服务次数left_ny, 如果满足这些条件就更新Customers_just_information和solution,并将最终的更新结果分别赋值给newCustomers_just_information与newsolution返回。 Customers_just_information=newCustomers_just_information; solution=newsolution; Mx,y=0; temp_M=M:; hs,wz=sorttemp_M, 1,'descend'; temp=findM~=0,1; break end if nx left_nx=fx-nx; 客户点x的剩余被服务次数 [newCustomers_just_information, newsolution]=Joint_point_to_endpoint(Customers_just_information, solution, y, x, left_ nx, p, q, Q); 调用函数Joint_point_to_endpoint来处理y为端点而x未被服务的那些时间段 Customers_just_information=newCustomers_just_information; solution=newsolution; Mx,y=0; temp_M=M:; hs,wz=sorttemp_M, 1,'descend'; temp=findM~=0,1; break end if nx left_ny=fy-ny; 客户点y的剩余被服务次数 [newCustomers_just_information, newsolution]=Joint_point_to_endpoint(Customers_just_information, solution, x, y, left_ny, p, q, Q); 调用函数Joint_point_to_endpoint来处理x为端点而y未被服务的那些时间段 Customers_just_information=newCustomers_just_information; solution=newsolution; left_nx=fx-nx; 客户点y的剩余被服务次数 [newCustomers_just_information, newsolution]=Joint_point_to_endpoint (Customers_just_information, solution, y, x, left_nx, p, q, Q); 调用函数Joint_point_to_endpoint来处理y为端点而x未被服务的那些时间段 Customers_just_information=newCustomers_just_information; solution=newsolution; ny=sum(Customers_just_informationy,1:); nx=sum(Customers_just_informationx,1:);
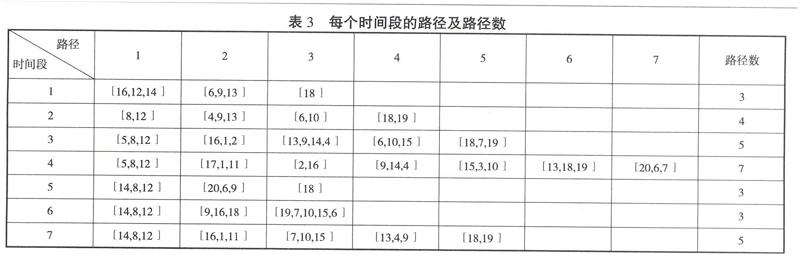
if nx [newCustomers_just_information, newsolution]=Creat_two_points_path (solution, f, Customers_just_information, nx, ny, x, y, p, q, Q); 生成新路径::车场→x→y→车场 函数Creat_two_points_path (solution, f, Customers_just_information, nx, ny, x, y, p, q, Q)首先寻找x,y都未被服务的时间段,如果这样的时间段存在,就计算x,y剩余被服务次数left_nx,left_ny将最小者记为Min_Left_Delivery_Times,接着判断路径:车场→x→y→车场在x,y都未被服务的时间段中是否可行,如果可行,就在这些时间段中个数不超过Min_Left_Delivery_Times的时间段里生成新路径:车场→x→y→车场,更新Customers_just_information和solution,并将最终的更新结果分别赋值给newCustomers_just_information与newsolution返回。 solution=newsolution; Customers_just_information=newCustomers_just_information; ny=sum (Customers_just_informationy,1:); nx=sum (Customers_just_informationx,1:); if nx [newCustomers_just_information, newsolution]=Creat_two_points_path (solution, f, Customers_just_information, ny, nx, y, x, p, q, Q); 生成新路径:车场→y→x→车场 solution=newsolution; Customers_just_information=newCustomers_just_information; end end Mx,y=0; temp_M=saving_values:; hs,wz=sort (temp_M, 1, 'descend'); temp=findM~=0,1; break end end end 此时所有客户点间的节约值都变成了0 for h=1:m 处理未达到其频率的客户 nh=sum(Customers_just_informationh,1); 客户点h已经被服务的次数nh if nh tem=find (Customers_just_informationh,1==0); 找到客户点h未被服务的所有时间段将它们存储在tem里 for h1=1: fh-nh 在客户点h未被服务的时间段里挑出其剩余频率fh-nh个时间段,单独派车对其进行服务 Customers_just_informationh,1temh1=1; solutiontemh1,1=solutiontemh1,1+1; solutiontemh1, solutiontemh1,1+1=h; end end end 3 例 子 在-500,500×-500,500的区域内随机产生21个点,第1个点为车场,其余的点为客户(如图1所示)。设一个周期为7个时间段,随机产生每一客户在周期内要求的服务次数(简称为频率)见表1,表2为每个客户在各个时间段的需求量和退货量。 根据本文所给出的改进的C-W节约算法,得到周期内每个时间段的路径及路径数见表3。表3中第k行第s列(如果不空)k=2-8,s=2-8给出第k-1个时间段的第s-1条路径,如第4行第5列为15,3,10,就表示第4个时间段第5条路径为:车场→客户点15→客户点3→客户点10→车场。 此例子中:①总的启动费用为:(3+4+5+7+3+3+5)×10=300; ②总的行驶费用为:5.0773e+004; ③总费用为:300+(5.0773e+004)=5.1073e+004。 4 结 论 本文对带退货的单车场周期车辆路径问题进行了描述,无论对于大型连锁超市还是供货商而言,此问题都有实际意义和商业价值。用MATLAB代码给出了求解该问题的C-W节约算法,通过例子表明所设计的算法操作简便,易于理解。 参考文献: [1] Beltrami E J, Bodin L D. Networks and vehicle routing for municipal waste collection[J]. Networks, 1974,4(1):65-94. [2] Ann M C, Jill H W. Forty years of periodic vehicle routing[J]. Networks, 2014,63(1):2-15. [3] Alper Hamzadayi, Seyda Topaloglu, Simge Yelkenci Kose. Nested simulated annealing approach to periodic routing problem of a retail distribution system[J]. Computers & Operations Research, 2013,40:2893-2905.
[4] Theodore A, Ioannis M. Efficient techniques for the multi-period vehicle routing problem with time windows within a branch and price framework[J]. Annals of Operations Research, 2013,206:1-22.
[5] Alireza R-V, Teodor GC, Michel G, et al. A path relinking algorithm for a multi-depot periodic vehicle routing problem[J]. Heuristics, 2013,19:497-524.
[6] Mohammad Mirabi. A hybrid electromagnetism algorithm for multi-depot periodic vehicle routing problem[J]. Int J Adv Manuf Technol, 2014,71:509-518.
[7] Phuong Khanh Nguyen, Teodor Gabriel Crainic, Michel Toulouse. A hybrid generational genetic algorithm for the periodic vehicle routing problem with time windows[J]. J Heuristics, 2014,20:383-416.
[8] V. Cacchiani, V. C. Hemmelmayr, F. Tricoire. A set-covering based heuristic algorithm for the periodic vehicle routing problem[J]. Discrete Applied Mathematics, 2014,163:53-64.
[9] Julien Michallet, Christian Prins, Lionel Amodeo, et al. Multi-start iterated local search for the periodic vehicle routing problem with time windows and time spread constraints on services[J]. Computers & Operations Research, 2014,41:196-207.
[10] Suyanto C, Herman M. A model for periodic vehicle routing problem with delivery and pick-up considering maximum distance[J]. International Journal of Science and Advanced Technology, 2014,4(8):1-9.
[11] Narges Norouzi, Mohsen Sadegh-Amalnick, Mehdi Alinaghiyan. Evaluating of the particle swarm optimization in a periodic vehicle routing problem[J]. Measurement, 2015,62:162-169.
[12] Mohammad M. A novel hybrid genetic algorithm for the multidepot periodic vehicle routing problem[J]. Artificial Intelligence for Engineering Design, 2015,29:45-54.
[13] Alireza Rahimi-Vahed, Teodor Gabriel Crainic, Michel Gendreau, et al. Fleet-sizing for multi-depot and periodic vehicle routing problems using a modular heuristic algorithm[J]. Computers & Operations Research, 2015,53:9-23.
[14] 姜贵山. 周期性车辆路径问题的引导式邻域搜索算法设计及应用[D]. 上海:上海交通大学(硕士学位论文),2010.
[15] 蔡婉君,王晨宇,等. 改进蚁群算法优化周期性车辆路径问题[J]. 运筹与管理,2014,23(5):70-77.
[16] Peter F, Karen S, Michal T. The period vehicle routing problem with service choice[J]. Transportation Science, 2006,40(4):439-454.
