巧妙入门，走进立体几何的趣味殿堂

颜艳

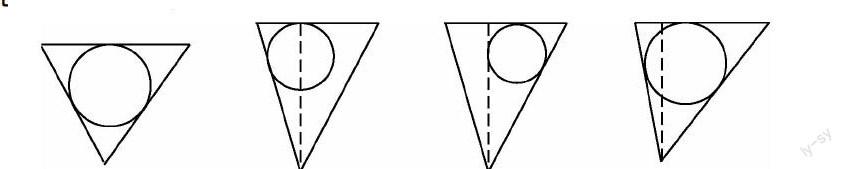
立体几何是高中数学当中的重要组成部分，甚至可以算是一个标志性内容.对于这部分知识，学生们的学习状态常常会呈现出较为明显的两极分化.有的学生认为，立体几何知识非常容易掌握，考试当中的立体几何问题往往都是送分题.然而，有的学生则将立体几何视为一座难以跨越的高山，总是观察不出位置关系，找不到解题方法.实际上，只要把握住了立体几何的基本知识与思维方法，巧妙入门，对其进行掌握并没有那么困难.

一、观察图形，培养空间想象能力

学习立体几何的基础不是那些具体的概念和性质，而是感官上的空间想象能力.如果不具备这个基本前提，又何谈从图形当中发现解题线索，并在图形的指引下开展探究呢？很多存在学习困难的学生都表示，常常看不出来图形当中线、面之间的位置关系，这就是空间想象能力出现了问题.这也是教师在带领学生们步入立体几何世界时，需要首先解决的问题.

例如，刚刚开始学习立体几何时，我便从一些基本和规则的图形开始，带领学生们进行观察，由图形读出其中的空间含义.同时，我还鼓励学生们自己动手画出立体几何图形，从比较简单的正方体、长方体，到复杂一些的球形、四棱锥等等.我还会不时地让学生们完成类似这样的习题：向倒置的正三棱锥容器内放入一个球，使其与容器四面均接触.过一条侧棱和高作截面，能够出现下列哪个图形？空间想象能力的培养，从不断地图形观察开始.

空间想象能力就像是立体几何学习过程当中的一门通用语言，只有具备了这个能力，才能谈到接下来的知识学习.众所周知，立体几何的内容呈现是离不开图形的，因此，会读图，做到会学习.知识入门阶段是空间想象能力建立的关键时期，教师一定要予以重视并牢牢把握，为接下来的教学奠定坚实基础.

二、立足教材，夯实基础性质定理

带着充分的空间想象能力，我们就可以带领学生开始具体知识的学习了.同其他内容的教学一样，基础知识是展开教学的必经之路.在立体几何教学当中，教师应当将学生们的初步关注重点集中在基本的性质定理之上.一方面，性质定理是学生们解决立体几何问题有效和直接的工具.另一方面，深入体会理解性质定理，也能够帮助学生强化知识体验，沿着合理方向启发思维.

例如，三垂线定理是立体几何当中非常重要的定理之一，因此，在这个内容的教学过程当中，我对于其内涵细节进行了着重剖析.从文字的表面含义入手，应当看到该定理的应用，即证明两条直线垂直，特别是在需要证明两条异面直线垂直的情况下.另外，还要找到应用这个定理时的关键点，即抓住平面与平面的垂线之间的关系.我还为学生们总结了一句顺口溜：“一个平面四条线，线面垂直是关键”.只有将定理理解到这个程度，才是将基础夯实了.

这个阶段的教学，并不需要教师花费过多的精力进行拓展，而是应当聚焦教材，对于教材当中出现的每个基本性质定理，进行深入挖掘和细致阐释，夯实知识基础.具体说来，可以从两个角度进行把握：首先，理解性质定理，即透过精炼的数学语言，对其内涵进行全面理解.其次，运用性质定理，只有在具体问题的解答当中能够迅速、准确地将相应性质、定理进行应用，才是真正的掌握了.

三、总结规律，形成问题解答体系

掌握了基本知识之后，接下来，就是对于立体几何学习进行提升的阶段了.虽然立体几何的问题内容与形式千变万化，但是，隐藏在其背后的解题思路与方法却并不那样繁杂.也就是说，只要掌握了典型的解题思维规律，便能够以不变应万变地解决各种立体几何问题了.这也足可以见得，问题解答思维体系的形成是何等重要.

例如，我曾要求学生们完成这样一道习题：正方体ABCD-A1B1C1D1的棱长是1，点P是侧棱CC1上的一点，且CP的长为m.若PA与面BB1D1D所成的角的正切值是32，求m的值.另外，A1C1上是否存在定点Q，使得对于任意的m都有D1Q在面PD1A上的射影与PA垂直.我先采用单纯的几何方法进行了推导，通过构造辅助线（如下图右）找到线面角，并根据三垂线定理进行求证.随后，我又借助空间直角坐标系的方式（如下图左），从坐标与向量的角度进行量化计算求证.这两种解答方法不是凭空出现的，而是从几何与代数的不同思维角度出发进行的具有方向的思考.

很多教师在立体几何教学中，都会陷入一个思想误区，认为解题思路的规律性总结是知识内容全部教学完成后要做的事，而非知识入门阶段的任务.这是有所偏颇的.数学思想方法贯穿于整个高中数学学习过程中，它是数学学习所必备的习惯性思考，它在学生们的头脑当中建立形成，也不是一蹴而就的.因此，随着知识的入门教学，教师就需要开始有意识地引导学生关注思想方法，进行有效总结，并逐步养成思维习惯了.

正所谓，难者不会，会者不难，这句话在立体几何当中体现得尤为明显.对于立体几何学习来讲，什么叫做“会”？笔者认为，第一，要从感性上具有一定的空间想象能力，这是感知立体几何的前提基础.第二，要熟练掌握教材上所出现的各种性质和定理，这是分析立体几何问题的有力武器.第三，要站在基礎知识之上，对于问题的解答过程进行提炼总结，找到其中的规律，指导同类问题的思考探究.按照这样的思维顺序，将学生带入立体几何的大门，相信定会让每名学生轻松接受，感受趣味.