“解决问题”教学三步曲
2016-05-30吴端彬
【摘 要】“解决问题”教学是小学数学教学的重要内容,也是教学的重难点之一。作为数学教师,我们要紧紧把握“以学生为本”的教学理念,结合学生的特点,合理挖掘和利用教育教学资源,通过阅读理解,分析解答与回顾反思等步骤,来探索“解决问题”的教学模式,提高“解决问题”课堂的教学效率。
【关键词】阅读理解 分析解答 回顾反思
“解决问题”教学是小学数学教学的重要内容,也是教学的重难点之一。在实际教学中,广大数学教师都有同感,在“解决问题”的教学中花了很大气力,但收效甚微。如何做到优化与“解决问题”教学的有效结合,关注“解决问题”的过程,寻求“解决问题”教学的优化模式,成为广大教师课改以来最感困惑而又无法回避的问题。为探索“解决问题”教学方法的优化,提高课堂教学效率,构建优质高效的“解决问题”课堂教学的模式,我在教学中紧紧把握三个步骤,尝试摸索着“解决问题”教学的模式。
一、阅读理解是前提
大多数人认为学生阅读理解能力的培养主要是语文学科的任务,其实不然,数学学习中也处处存在阅读理解,特别是“解决问题”的教学。“解决问题”是一个完整的知识结构系统,是用一定的情节来描述数量关系的数学问题。阅读能力强的学生,对文字和图形的感知、理解和转换的能力也比较好,能够摆脱一定的情境因素在头脑中清晰地抽象出数学问题,能够成功地做出解答。对于高年级的学生,我通常训练他们分三个步骤来进行“解决问题”的正确阅读,即泛读、细读与精读。首先泛读,就是粗粗地读一遍,大概了解题目内容讲的是什么事情。第二遍细读,找出题目中关键的词句,重要的数量。第三遍精读,抓住题目中关键的数学信息点,明确题目的隐含信息,因为抓住了这些信息点,就像拿到了“解决问题”的钥匙。
例如,人教版第十册教材“一个长方体,如果高减少3厘米,就成为一个正方体。这时表面积比原来减少了96平方厘米,原来长方体的体积是多少立方厘米?”看似简单的一道“解决问题”,却难倒了很多学生,如果阅读理解不过关,单靠套用长方体的有关计算公式,根本無法解答。于是我这样引导学生阅读:
师:这道题主要讲什么事?
生:一个长方体,变成一个正方体(泛读)
师:为什么会变成正方体?变成正方体后还引起什么变化?
生:长方体高减少,变成正方体,表面积也减少。(细读)
师:‘高减少,变成正方体,隐含着什么重要的信息?(大部分学生被卡住了)
师:什么样的长方体高减少后才会变成正方体?(这时一些学生想到了特殊的长方体)
生:哦,原来这个长方体的底面是正方形(精读)
经过一番认真的阅读理解,学生对题目的核心已掌握,为下面的分析与解答环节奠定了坚实的基础。
对于低年级的“解决问题”的阅读,主要是引导他们读懂插图的意思。新课程标准的“解决问题”教材一反传统教材应用题的呈现模式,变呆板、枯燥、沉闷为生动、充满生命活力的情景,图文并茂、数形结合是新教材的一个特点,特别是低年级的数学教材中,插图的分量很大。低年级学生因为不会阅读插图,不明白其中的含义而给“解决问题”带来了很大的麻烦。因此教学“解决问题”时教师要在阅读插图方面给学生必要的指导。
在“解决问题”的教学中,学生只有在阅读理解环节过关了,才能为分析与解答环节扫清障碍,所以阅读理解也是“解决问题”的必要前提。
二、分析解答是关键
通过阅读理解掌握了题目的基本数量关系后,能否顺利地解答,关键在于是否掌握了分析“解决问题”的方法,在于学生能否在已有信息与问题之间找出某种联系。
这里还是以人教版第十册教材“一个长方体,如果高减少3厘米,就成为一个正方体。这时表面积比原来减少了96平方厘米,原来长方体的体积是多少立方厘米?”为例:
学生通过前面的阅读理解已经明白原来长方体的底面是正方形后,教师就引导学生分析:表面积减少96平方厘米是减少前后左右4个面的面积,因为底面是正方形,所以96平方厘米就是4个面积是相等的长方形面积的总和,那么一个面的面积是96÷4=24平方厘米,底面的长是24÷3=8厘米,说明原来长方体的长和宽都是8厘米,也就是变成正方体后的棱长是8厘米,高减少3厘米后是正方体,那原来长方体的高是3+8=11厘米,所以原来长方体的体积是8×8×11=704立方厘米。
这样亦步亦趋引导学生通过分析探寻,顺藤摸瓜,捋顺了题目的数量关系,探求解题思路,最后顺利完成问题的解答,有效实现了“解决问题”的教学目的。
此外教师还可以引导学生通过画图来帮助分析,把抽象的数学内容变得形象生动,把“解决问题”的策略图形化,以便更好地解答。
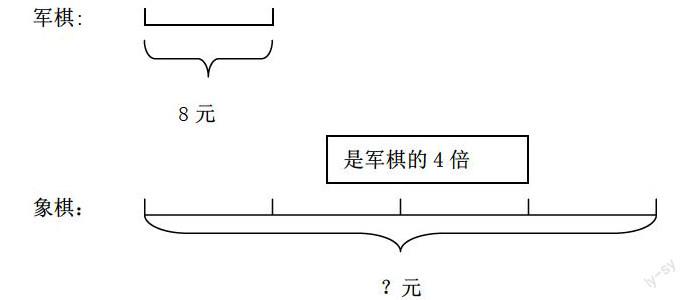
例如,人教版数学第五册的“军棋的价钱是8元,象棋的价钱是军棋的4倍。象棋的价钱是多少元?”学生对“倍”的理解比较抽象,有一定的难度。教师可以用直观的画图来帮助学生理解分析。
通过这样的线段图,学生很容易看出要求“象棋多少元,就是求4个8是多少”,用乘法计算。
三、回顾反思是提升
“学而不思则罔”,如果解决完问题后不进行回顾反思,那么学习将停留在表面,只是单纯为了求得问题的结果。这样不利于学生解题能力的培养,数学思维的训练与提升。在“解决问题”以后,再回过头来对解题活动加以回顾反思是数学教学非常重要的一个环节,这一环节可以帮助学生从解题中总结出数学的基本思想和方法,加以掌握,并将它们用到新的问题中去,成为以后分析和解决问题的有力武器。
例如,人教版第九册教材“小林家和小云家相距4.5km.周日早上9:00两人分别从家骑自行车相向而行,小林每分钟骑250m,小云每分钟骑200m,两人何时相遇?”
学生解答完后教师说道:“大家回顾一下我们刚才的解题过程,你有什么收获?”学生们静下心把刚才分析解答的过程进行了一番回顾与梳理,概括出了用方程解答问题的分析方法,解题思路等。有的学生说:“我们通过画线段图可以清楚地分析数量之间的相等关系,以后我们在解决类似的问题时也可以这样做。”有的学生说:“这里要用到速度、时间和路程的数量关系来列方程。”还有的学生说:列方程“解决问题”最关键的是找出数量间的相等关系”……
通过回顾反思,不但促进学生牢固掌握本节课的知识,提高他们的解题能力,而且有效促进学生总结概括能力的培养,促使学生积累基本经验,促进思维的发展。
“解决问题”的教学是新课程标准人教版教材的一道亮丽的风景,作为一线的数学教师,我们要紧紧把握“以学生为本”的教学理念,结合学生的特点,合理挖掘和利用教育教学资源,通过阅读理解,分析解答与回顾反思三个步骤的有机结合,来探索“解决问题”的教学结构、促进教学方法的优化,提高“解决问题”课堂的教学效率。
作者简介:吴端彬,女,生于1973年1月,福建连江人,汉族,福建省福州市连江县敖江中心小学,一级教师,研究方向:小学数学。
