风力机翼型气动性能数值模拟方法研究

摘 要：采用三种数值模拟方法对风力机翼型气动性能进行模拟，并与实验值进行对比，验证了数值模拟方法的可靠性。结果表明，不同模拟方法对于不同的流动状态有各自的优势，在进行翼型气动模拟时需考虑数值模拟方法的选择。

关键词：气动性能；数值模拟方法；风力机翼型

风轮叶片是风力机获取风能的关键部件，翼型的气动性能是风轮叶片性能的基础，直接影响着风力机的风能利用[ 1，2 ]。而精确的数值模拟方法是分析翼型气动性能以及为相关工程模型提供基础数据的保证[ 3 ]。

WJ Zhu等[ 4 ]采用势流-边界层耦合方法对翼型进行了优化设计，并获得了气动性能较好的翼型外形。

高伟等[ 5 ]采用势流-边界层耦合方法对不同厚度翼型边界层转捩进行了研究，结果表明转捩位置对翼型升阻力系数有一定影响。

马林静等[ 6 ]采用S-A湍流模型及另外两种湍流模型对S809翼型气动性能进行了模拟，并与实验值对比，表明S-A模型整体计算精度相对较高，收敛性最好。

刘磊等[ 7 ]采用几种湍流模型对某风力机进行了数值模拟，结果显示全湍流模型SST k-w对截面压力以及转矩分布计算较为准确，尤其是叶片表面开始出现分离的情况。

S？覬rensen等[ 8 ]在SST k-w湍流模型中加入间歇因子-动量厚度雷诺数（γ-Reθ）转捩模型，即T-SST湍流模型，模拟结果比全湍流模型模拟结果更为准确。

对于风力机翼型，不同的模拟方法得出的计算结果不同，较少有文献对模拟方法进行较为综合的分析。且相关文献在对模拟方法分析与使用中，也很少考虑网格结构、流动状态与湍流模型之间的相互关系与需求。

鉴于此，本文以具有实验数据的S809翼型[ 9 ]为研究对象，在充分考虑网格结构的基础上，分析不同流速时各数值模拟方法对翼型计算结果的影响。主要涉及势流-边界层耦合方法和基于S-A湍流模型与T-SST模型的CFD方法。

1 数值模拟方法

1.1 势流-边界层方法

Prandtl于1904年提出边界层的概念，并认为对于空气等黏度较小的流体，当雷诺数Re较大时，流体黏性的影响仅限于边界层中，边界层之外的流体黏性可以不考虑[ 10 ]。风力机叶片流体Re多为5×105～3×106，为大雷诺数流动，已然可用此求解方法。Drela教授将势流方程与边界层方程耦合，并运用en法来预测边界层转捩，开发对翼型的快速数值分析软件Xfoil[ 11 ]。此方法一定程度上反映了流体流动的粘性效果，且对流动的转捩有较好的预测。

1.2 CFD方法

Spalart-Allmaras（S-A）模型为一方程模型，能够较好预测具有逆压梯度的束缚流动，对于翼型、墙壁等壁面流动可以得出较好的结果[ 12 ]。

在对壁面边界层的处理上，S-A模型将流动假设为全湍流流动，忽略了流体在壁面由层流向湍流转捩。T-SST为全湍流模型SST k-w模型与间歇因子-动量厚度雷诺数（γ-Reθ）转捩模型耦合得到的四方程模型。

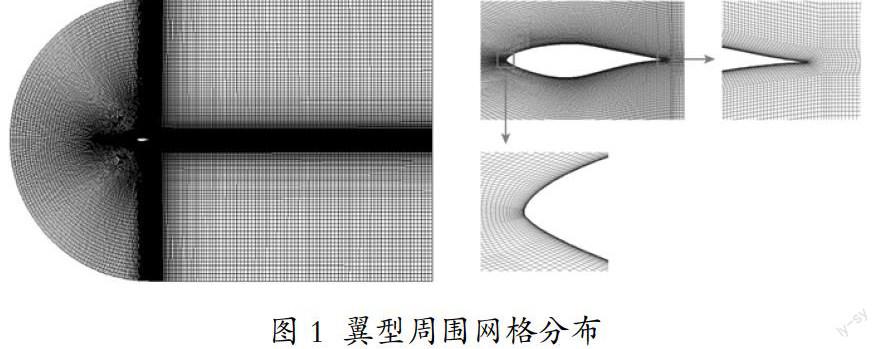
CFD计算模型采用结构化网格，对于翼型表面节点的布置，遵循能够较好体现翼型外形与捕捉流场细节的要求，对曲率较大与流动复杂位置进行节点加密。

本文取第一层网格厚度为1×10-5m，对应y+值小于1。翼型网格分布如图1所示。

计算域采用C型计算域，计算域边界距翼型至少10倍翼型弦长，尾流区域为25倍弦长。采用速度进口、压力出口边界条件，叶片表面设置为无滑移固体壁面。其中进口速度对应雷诺数Re=2×106，攻角（AOA）范围为-3°？燮？琢？燮18°。

2 结果与分析

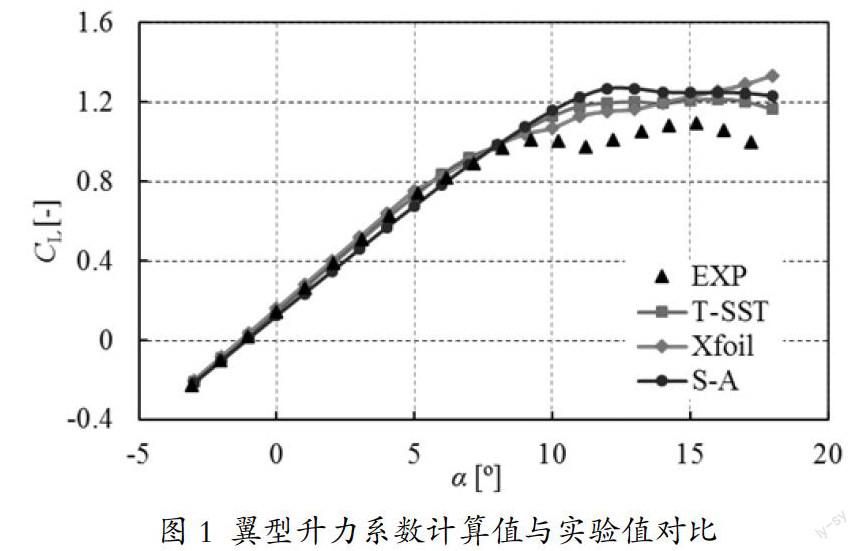
由实验结果可以看出，在攻角较小时，翼型升力系数随攻角的增大线性增大，并在攻角6°时出现增大减缓的现象，进入非线性增大区，此时翼型后缘已出现轻微分离。攻角10°时升力系数开始下降，并且在攻角11°位置达到一个极小值点后继续增大，在攻角15°左右达到升力的最大值。

从模拟值来看，在攻角9°以前模拟值均与实验值较为接近，此时流动基本为附着流状态或轻微分离状态。且Xfoil计算结果较好地体现了线性区域非线性区的位置。两种不同湍流模型的CFD方法尤其是S-A模型对于线性区范围预测较宽。

随着流动分离的进一步加深，模拟值与实验值出现较大误差，其中S-A湍流模型预测极大值点误差为17%，T-SST湍流模型预测极大值点误差为11%。

从整体升力系数随攻角的变化趋势来看，T-SST模型较好的预测出实验值中升力系数在11°位置下降后又上升的过程，尽管S-A模型亦在15°时有一定的体现，但并不明显。

Xfoil的计算结果在流动分离加深后，其升力系数随攻角的增大而持续增大，不仅未出现升力下降后上升的现象，亦未出现流动大分离后的升力系数降低。

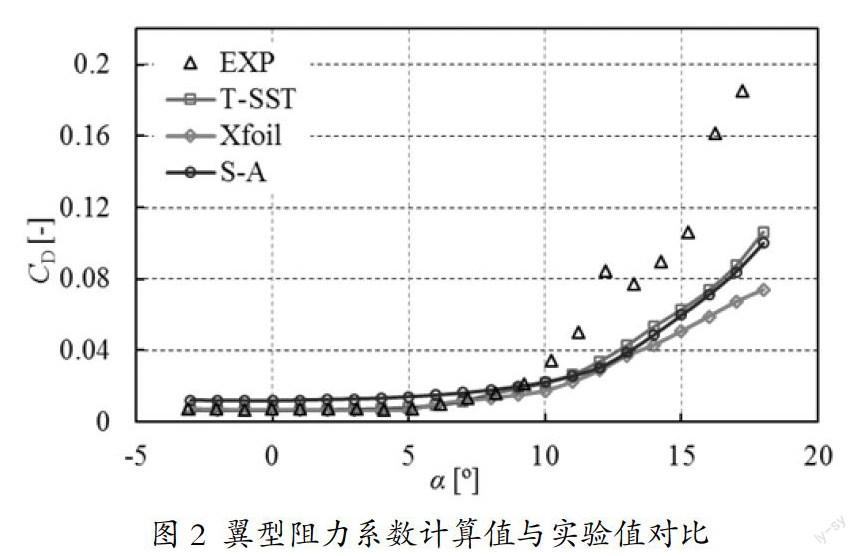
由图2可以看出，在攻角较小时，阻力系数实验值较小且几乎不变，攻角6°后出现上升趋势，并在攻角10°后出现急剧上升。Xfoil与T-SST模型由于加入了转捩预测方程，能够预测边界层内层流向湍流转捩，均较好的预测了附着流动与轻微分离时阻力系数的变化，且在数值上比较吻合，当阻力系数出现急剧上升时，模拟值均未有较好的预测，仅在趋势上有所体现。

S-A模型将流动假设为全湍流，不能预测边界层内的层流现象，在附着流区对阻力的预测偏大，分离区与T-SST预测值较为吻合。

由以上分析可知，在预测翼型宏观气动特性方面，基于势流-边界层方程的方法在翼型附着流动与轻微分离流动时具有较好的表现，且其计算快捷高效，优于CFD方法。

CFD方法在附着流动时的表现稍逊于势流-边界层耦合方法，但整体差别不大，分离流动时对翼型气动特性预测优于势流-边界层耦合方法，且高精度的湍流模型T-SST在细节捕捉上优于单方程S-A模型，转捩方程的添加可较好地预测翼型附着流区的阻力。

3 结论

通过以上对数值模拟方法的分析比较，可以看出，不同模拟方法在对不同的流动状态有各自的优势。附着流状态时Xfoil由于计算快捷准确，优势较大，分离流状态时CFD方法表现较好，且高精度T-SST模型表现最佳，并能较好地捕捉流场细节变化。在模拟翼型气动特性时，可考虑将势流-边界层耦合方法与高精度T-SST结合，以气动參数趋势变化点作为转折点，分别对翼型气动特性进行模拟，获取较为准确的计算值。

参考文献：

[1] 陈亚琼，方跃法，郭盛等.风力机专用翼型综合优化设计方法[J].中国机械工程，2015，29（9）：1194-1200.

[2] 叶舟，郝文星，祖红亚等.尾缘修剪对风力机翼型气动性能的影响[J].动力工程学报，2015，35（7）：593-598.

[3] Bergami L，Riziotis VA，Gaunaa M.Aerodynamic response of an airfoil section undergoing pitch motion and trailing edge flap deflection： a comparison of simulation methods [J].WIND ENERGY，2015，18（7）：1273-1290.

[4] Zhu WJ，Shen WZ，Sorensen JN.Integrated airfoil and blade design method for large wind urbines [J].RENEWABLE ENERGY，2014，70：172-182.

[5] 高伟，李春，高月文等.几何参数对风力机翼型转捩特性的影响[J].动力工程学报，2013，33（6）：490-496.

[6] 马林静，陈江.风力机翼型气动特性数值模拟[J].太阳能学报，2010，31（2）：203-209.

[7] 刘磊，徐建中.湍流模型对风力机叶片气动性能预估的影响[J].工程热物理学报，2009，30（7）：1136-1139.

[8] S？覬rensen N N. CFD Modelling of Laminar-Turbulent Transition for Airfoils and Rotors using theγ-Reθ Model [J].Wind Energy，2009，12（8）：715-733.

[9] D.M.Somers.Design and Experimental Results for the S809 Airfoil[R].NREL/SR-440-6918.Golden CO，Jan，1997.

[10] Anderson J D.Ludwig Prandtl's Boundary Layer [J].Physics Today，2005.

[11] Drela.XFOIL：An analysis and design system for low Reynolds number airfoils[C].Indiana： University of Noire Dame，1989.

[12] P.Spalart and S.Allmaras.A one-equation turbulence model for aerodynamic flows.Technical Report AIAA-92-0439.American Institute of Aeronautics and Astronautics.1992.

作者简介：王琳琳（1989-），女，硕士。