板材轧制过程中设定初始速度场的类电磁机制算法

刘静宜 薛翠平 秦浩玮

摘 要：采用Newton-Raphson（NR）算法求解有限元离散化后形成的非线性方程组时，初速度场的设定对迭代过程能否收敛或收敛时的迭代次数都有重要影响，设定初速度场是技巧性很强的工作。本文提出设定板材轧制过程中初始速度场的类电磁机制（EM）算法，首先将能耗率泛函表达为节点速度的函数，然后采用随机策略产生一组可行速度场（对应一群带电粒子），最后根据粒子对应的能耗率泛函目标值来确定粒子间的吸引与排斥机制，按照一定的准则使得粒子朝最优解方向移动。数值实验结果显示，类电磁机制算法能为NR算法提供可快速收敛的初始速度场。

关键词：类电磁机制算法；节点速度场；总能耗率泛函；刚塑性有限元

随着轧钢生产和轧制技术的快速提高，控制参数越来越多，产品精度要求越来越高，各种高新轧制技术层出不穷，使得传统工程法在应用中显得力不从心。现代优化方法中的智能优化借助计算机的快速计算，往往可以实现短时间、大数据、高效率的求解，在轧制过程的应用上也初步显现出其优势[ 1 ]。

在刚塑性有限元的求解过程中通常采用NR法[ 2 ]，当目标函数的二阶偏导数矩阵（Hessian矩阵）可求，且能给出较好初值的情况下，用NR法求解非线性方程组的收敛速度是很快的。但NR法是局部收敛的，对初值的要求较严格，初速度场的设定对迭代过程能否收敛或收敛时的迭代次数都有重要的影响。

初速度场的设定必须满足速度边界条件、不破坏速度连续条件、近似满足体积不变条件，主要方法有工程法、G函数法、细分单元法、经验法和近似场法。其中工程法适用于边界条件较为简单的情况，主要通过求得近似速度场作为初始速度场；经验法和近似场法相对比较复杂，主要根据一定的实验数据和变形数据进行类推和修正相近条件的速度场；G函数法通过求解近似泛函得到初速度场；在迭代求解过程中，细分单元法通过已知速度场对变形体进行单元细分和速度插值，作为下步迭代求解的初始速度场。随着计算机技术的发展，在运用刚塑性有限元求解板材轧制过程中，智能优化算法也被用来设定初始速度场[ 3 ]。文献[ 4 ]采用神经网络法设定刚塑性有限元求解板材轧制过程的初始速度场，首先对有限元计算结果或者实测数据通过有限元进行神经网络训练，获得速度场分布有关模型，利用此模型设定初始速度场。本文研究了类电磁机制算法[ 5 ]设定初始速度场，模拟电磁场中的吸引-排斥机制使搜索粒子朝最优解方向移动，并根据实际轧制数据进行了迭代求解和计算效率分析。

1 总能耗率泛函关于节点速度分量的表达形式

采用类电磁机制算法求解板材轧制问题时，应将总能耗率泛函表示为节点速度分量的函数。对平面变形条件下的简单轧制问题，单元能耗率泛函由塑性变形功率泛函φep和摩擦功率泛函φef组成，对不在接触表面上的单元， φef = 0 。当单元内所含节点的速度及速度分布规律设定之后，该单元的变形速度场ij及等效变形速度便已经确定，而相对滑动速度可以根据轧辊线速度与单元边界上的速度分布算出。这样，在给定材料的屈服应力和摩擦条件的情况下，单元能耗率泛函可以表示为单元所含节点速度的函数，再对所研究区域的全部单元求和，除去已知条件之后，把各节点的未知速度分量统一表示，则可把总能耗率泛函写成未知速度分量的函数。

为进行数值计算，必须对总能耗率泛函进行离散化，并详细写出泛函与节点速度的函数关系。刚塑性有限元求解过程中常采用高斯积分，即按照数学上的规则在单元内选取若干个积分点，用积分点处的函数值与求积系数之积的累加和来近似代替原积分。在平面变形条件下，根据变形速度、体积变形速度和节点速度的关系，可以写出单元塑性变形功率與节点速度的关系；根据相对滑动速度和节点速度的关系，可以写出单元摩擦泛函功率与节点速度的关系。由此总能耗率泛函与节点速度的关系如下：

这里n为单元总数，m为接触表面上的单元数， 为等效应力，bi，ci是形函数Ni（ξ，η）对x及y的偏导数，可由复合函数的偏微分法则求出，νxi，νyi为节点速度分量，mf为速度敏感系数，τk为屈服剪应力，Δνf=为相对滑动速度。

2 类电磁机制算法

类电磁机制算法根据电磁理论中的吸引—排斥机制把每个搜索粒子想象成空间中的一个带电粒子，其所带电量由目标函数值决定，并由所带电量决定该粒子对其他粒子吸引或者排斥的强弱，即目标函数值越优作用力越强，反之，作用力越弱。

类似电磁力的计算方式，EM算法根据所带电量为每个粒子寻找下一步的移动方向，通过将其他粒子施加给当前粒子的合力进行矢量叠加来确定该粒子的移动方向。同时EM算法采用局部搜索改进当前种群的目标函数值，当迭代次数趋于极限值时，种群至少有一个粒子以概率1移动到全局最优解附近。利用EM算法求解板材轧制问题时，计算过程主要包括初始化、局部搜索、计算电荷量、计算合力及移动粒子五个步骤：

1）初始化：在可行域中随机释放m个样本点{ν1，ν2，ν3，···，νm}，使样本点的坐标在上下界中均匀分布。样本点的目标函数值由函数φ给出，并将最优解粒子记为νbest。

2）局部搜索：EM算法采用随机线性搜索算法进行局部搜索。首先设定局部搜索的迭代次数和决定搜索范围的因子，对当前粒子的每个移动方向根据局部搜索因子确定可行移动步长，然后按照该步长进行搜索，找到比当前最优解更好的解则停止局部搜索过程，并更新最优解的信息。局部搜索可以用于当前所有粒子，也可以只对当前最优粒子进行。

3）计算电荷量：粒子的电荷量由目标函数值决定。由于粒子在不断更新，故每次迭代过程中粒子的电荷量也会发生变化。EM算法中粒子i的电荷量表示如下：

由上式可知，目标函数值越优，粒子电荷量越大，且每一个粒子电荷量都是（0，1]之间的正实数。计算电荷量时将函数的维度n作为因子体现在公式中，是为了抑制在求解电荷量时由于较高维度函数所用的粒子规模较大导致分数过小造成计算溢出的问题。

4）計算合力：根据电磁学理论中的叠加原理，某粒子所受的其他粒子的电磁力与他们之间的距离成反比，与电荷量成正比。因此，作用在粒子i上的合力Fi由下式给出：

5）计算过程中并没有对电荷进行正负标号，而是在比较两点目标函数值后再确定一个力的方向。由公式（3），在两点中具有更优目标函数值的粒子将会吸引另一个粒子。相反地，具有更劣目标函数值的粒子将会排斥另一个粒子。因为νbest有最小的目标函数值，所以它扮演绝对吸引的角色。也就是说，它吸引着粒子群中所有的点。

6）移动：在计算合力向量F i之后，粒子i沿合力方向移动一个随机步长。这里假定随机步长λ服从0到1的均匀分布。公式（4）中，RNG是沿合力方向朝上界μk或者下界lk移动的可行步长。同时，由于作用在每个粒子上的力都被归一化了，从而保证了移动的可行性。粒子按照公式（4）移动后，即实现了EM算法的一次迭代过程。

7）收敛判据：EM算法常用的一种收敛判据是控制最大迭代次数。测试结果表明，通常在进行每个维度25次的迭代后，可以满足收敛到最优点的条件。另一种收敛判据是控制保持当前最优点不变的连续迭代数。若程序在若干步迭代后最优点不变，则迭代过程结束。当采用后一种收敛判据时，应避免出现早熟收敛，即粒子不容易摆脱当前最优点的束缚，无法逃离导致算法过早收敛的现象。

3 类电磁机制算法的实验结果和分析

为验证EM算法在模拟板材轧制过程中初速度场设定时的算法性能，采用如下现场轧制数据进行数值模拟。轧辊半径：405mm，轧辊线速度：1100mm/s，轧件轧制前厚度：53.890mm，轧件轧制后厚度：37.980mm，轧件宽度：1550mm，摩擦因子tm：0.45，摩擦系数tf：0.5，可压缩参数f：100。首先在空间中随机释放若干个粒子，计算当前目标函数取最优值时对应的粒子，记为νbest。其次根据现场轧制数据给出初始化节点速度分量的上下界：νx∈[0，1500]，νy∈[-200，0]。

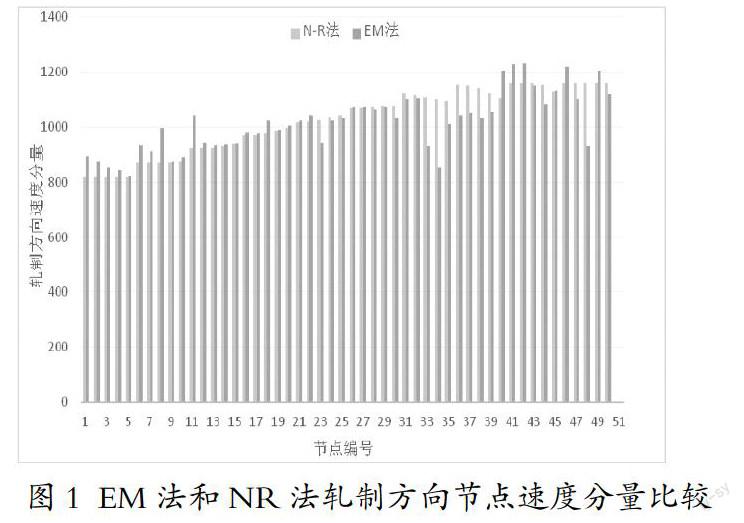
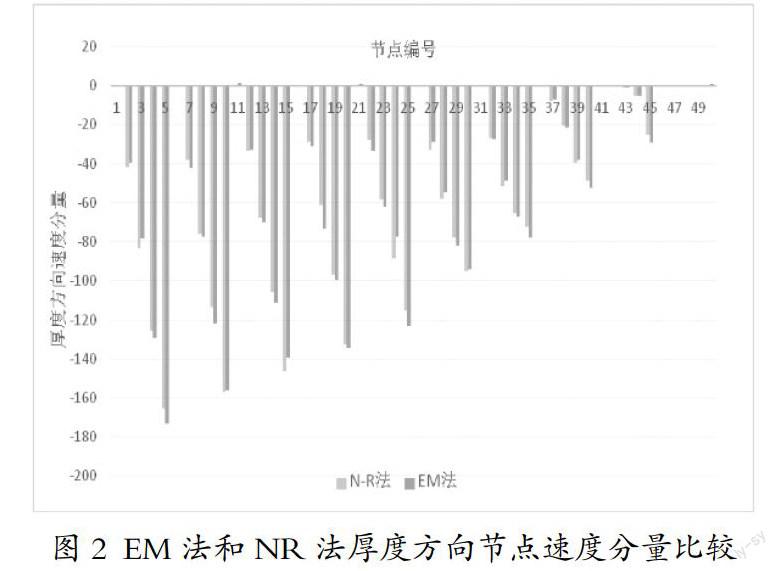
由图1和图2可以看出，迭代终止时EM算法训练出的初速度场已经非常接近由同组轧制数据，依靠NR法得出的总能耗率泛函取极小时的节点速度场，同时由于EM算法不需要计算一阶和二阶偏导数，计算速度得到明显提升。但由于EM算法早熟收敛现象，仍有个别节点速度分量误差较大。

EM算法虽然在某些程度上存在求解精度的缺憾，却可以作为NR法的前置算法，利用计算机模拟种群快速、简便的特性，跳过斋藤公式、中性角公式，避开运动许可条件和平断面假设的限制。

在适当的迭代次数终止智能优化过程，将此时的节点速度分量组成的速度场作为NR法的初速度场带入在线计算，从而达到短时间内为最优化方法提供可以快速收敛的初速度场的要求。

4 结论

本文针对板材轧制过程中初始速度场的设定问题，提出了基于种群理论的类电磁机制算法。EM算法在求解这类问题时具有传统优化方法无可比拟的优越性。

传统优化方法过分依赖初始点的设置，例如采用NR法求解时，若选择远离全局最优解的初始点，则迭代过程中目标函数值下降缓慢。另外，NR法对目标函数的解析性质要求较高，同时计算一阶和二阶偏导数的过程也耗费了大量的计算时间，难以满足在线应用的要求。

随着初始样本点数量的增多，以及粒子上下界选取的精确，EM法能够快速收敛到全局最优解附近，为进一步采用N-R法求解，提供一个可快速收敛的初始速度场。

参考文献：

[1] Jiang Z Y，Tieu A K，Lu C，et al.Three-dimensional thermo-mechanical finite element simulation of ribbed strip rolling with friction variation[J].Finite elements in analysis and design，2004，40（9-10）：1139-1155.

[2] 刘相华.刚塑性有限元及其在轧制中的应用[M].北京：冶金工业出版社，1994.

[3]Xu W L，Di S L，Thomson P. Rigid-plastic rigid-viscoplastic FE simulation using linear programming for metal forming [J].International Journal for Numerical Methods in Engineering，2003，56（4）： 487-506.

[4] Gudur P P，Dixit U S.A neural network-assised finite element analysis of cold flat rolling[J].Engineering applications of artificial intelligence，2006，21（1）：1-10.

[5] BIRBIL S I，Fang S C.An electromagnetism-like Mechanism for global Optimization[J].Journal of global Optimization，2003，（25）：263-282.