基于高速列车模态分析的试验方法研究

薛蔚

摘要：采用试验模态和运行模态两种试验研究方法，对某型高速列车整备状态下的车体模态展开研究，运用PolyMax及FSDD两种方法对模态参数进行识别，分别得到车体刚体模态和低阶弹性模态参数，并将分析结果进行对比验证。

关键词：模态试验；EMA；OMA；激振器；整车振动台

中图分类号：TB

文献标识码：A

doi：10.19311/j.cnki.16723198.2016.13.101

随着我国高速铁路的迅猛发展，运行速度的不断提升导致了外界激扰频率的增加，由此带来的结构振动问题直接影响了车辆运行的安全性。其中，车体的振动模态与列车的乘坐舒适度存在直接联系，而这种复杂结构在生产制造的过程中不可能随意修改，一旦完工，其动力学特性就已确定，如何准确的测得其模态参数，为SDM问题提供第一手数据，就显得尤为必要。本文就是基于这样的目的，采用不同的激励方法和参数识别方法，对某型高速列车整备状态下的车体模态展开研究。

1 模态基础

模态，指的是结构的固有振动特性，每一个模态具有特定的固有频率、阻尼比和模态振型。所谓模态分析，就是将线性定常系统振动微分方程组中的物理坐标变换为模态坐标，使方程组解耦，成为一组以模态坐标及模态参数描述的独立方程，以便求出系统的模态参数。模态分析的最终目标是识别出系统的模态参数，为结构系统的振动特性分析、振动故障诊断和预报以及结构动力特性的优化设计提供依据。目前常见的分析手段有仿真分析法和模态试验法。整备车辆由于结构复杂，车下设备较多且吊挂方式多样，仿真建模难度较大，故而选择试验分析的方法来研究车体的模态参数。

2 试验方法

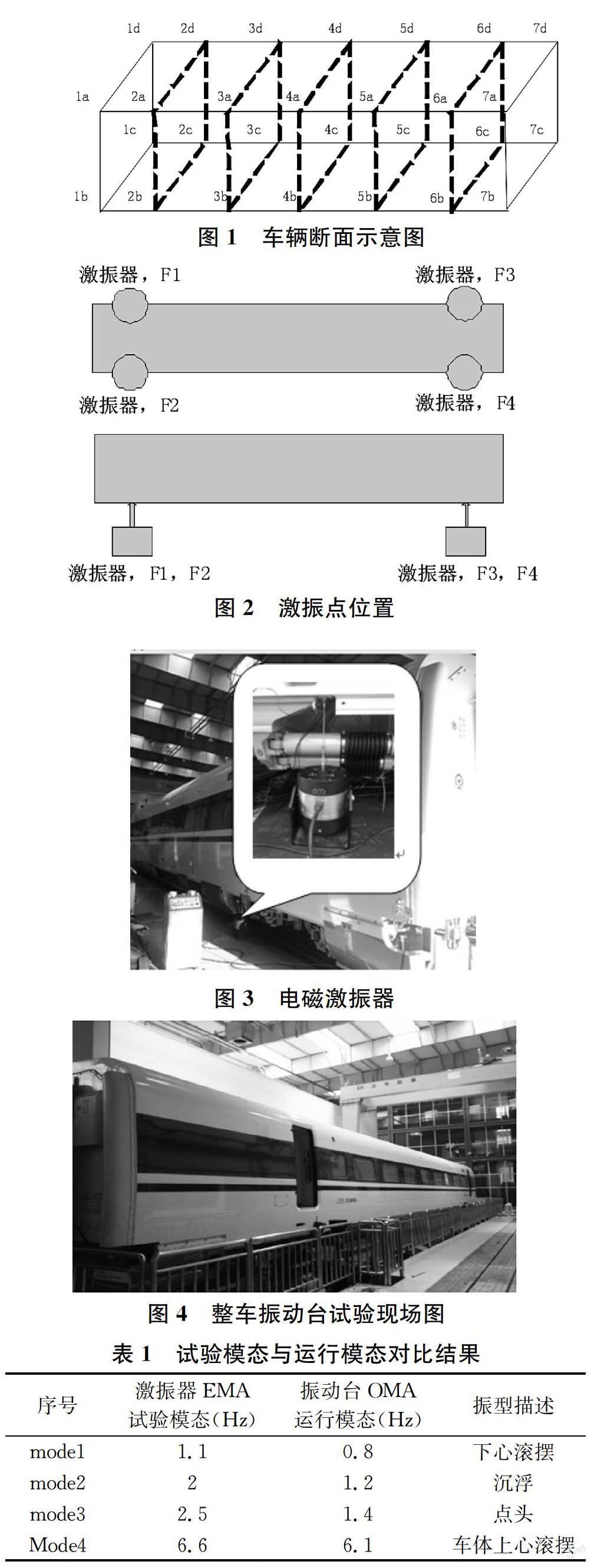
本次的研究对象为某型高速列车的整备车体，单节列车的车体长度大约为25米，为了准确描述车体的振型规律，将车体分为7个断面，每个断面采用4个点，每个点再布置垂向和横向的两个加速度传感器，共计56个加速度测点。采用基于LMS的Test.Lab测试系统来完成数据采集工作。然后按照试验模态和运行模态两种试验激励方法分别进行试验。

2.1 EMA试验模态激励方法

采用多个激振器同向多点随机激励，激励信号为0-50Hz范围内的猝发随机信号。激振点选择在车体抗蛇形减震器的安装座的位置，如图2所示。这个位置安装便利且刚度相对够大，能够将激振器的激励信号很好的传递到车身的各处。激振器是通过柔性激振杆连接到车身的。激振杆一端刚性连接到激振器上，另一端安装有力传感器，力传感器刚性安装在车身上，以实现激振器与车身的连接。现场激振器的安装如图3所示。

2.2 OMA运行模态激励方法

为了在实验室中达到运行模态的试验工况，本次试验使用了先进的整车振动实验台。将整车安放至试验台上，固定车轮以防止车辆在试验时发生倾覆，调理出0-20Hz的白噪声信号激励轮对，模拟车辆运行时的宽频激励状态。

3 两种参数识别方法

为了确保试验结果的准确性和重复性，本次试验采用了两种模态参数识别方法。一种是基于LMS的PolyMax分析法，还有一种是基于N-Modal软件的FSDD分析法。

比利时LMS公司开发的PolyMAX方法是一种全新的频域分析方法，该方法也被称为多参考最小二乘复频域法（LSCF）。其识别步骤与最小二乘复指数法（LSCE）很类似。LSCE法是一种时域分析方法，在处理频率较高且模态密集的系统时易产生虚假模态，其稳态图较混乱，模态定阶较难，效果较差，难以取得较理想的结果。而PolyMAX方法的主要好处：一是SVD（奇异值求解）这一步骤能避免留数的分解，密集空间可以分离出来。二是该方法既适用于弱阻尼，也适用于强阻尼，密集模态系统的参数识别。三是在强阻尼、密集模态情况下，仍可获得非常清晰的稳态图，从而很容易实现物理模态定阶，结果的客观性更好。EMA试验就采用这种参数识别方法。

第二种方法是FSDD法（Frequency and Spatial Domain Decomposition），是一种OMA的频域空间域分解法，最早是由南京航空航天大学的张令弥教授提出的。该法可视作EMA 的经典方法CMIF（Complex Mode Indicator Function）在OMA中的拓展。CMIF建立在对多参考点频率响应函数（Frequency Response Function，FRF）矩阵的奇异值分解基础上，最初仅作为确定系统模态阶次的指示因子，而后进一步发展为一种两步式的MIMO的模态参数识别方法：第一步中，奇异值曲线的峰值点给出了系统的阻尼自然频率，相应的左奇异值向量与模态振型成比例，右奇异值向量则与模态参与向量成比例；第二步中，以上述的模态振型与参与向量作为加权函数，得到对应各模态的单自由度FRF，在频域里以单自由度算法识别得到准确的自然频率与阻尼比。OMA试验就采用这样的识别方法。

4 试验模态和运行模态的结果对比

使用两种方法对试验数据进行分析后，得到整备车体的刚体模态和弹性模态结果，包括模态频率和振型特征。

4.1 整车刚体模态的试验结果对比

图5-图8为各阶模态振型的对比图，其中，左侧灰色背景为EMA试验方法下，PolyMax方法得到的模态结果，右侧白色背景为OMA试验方法下，FSDD方法得到的模态结果。

根据上述结果可以看出，电磁激振器试验模态的刚体模态结果比整车振动台模拟运行的刚体模态频率略高。判断这一现象与不同模态试验过程中激励能量的大小、作用点位置，以及车辆悬挂部件中的非线性等因素相关。

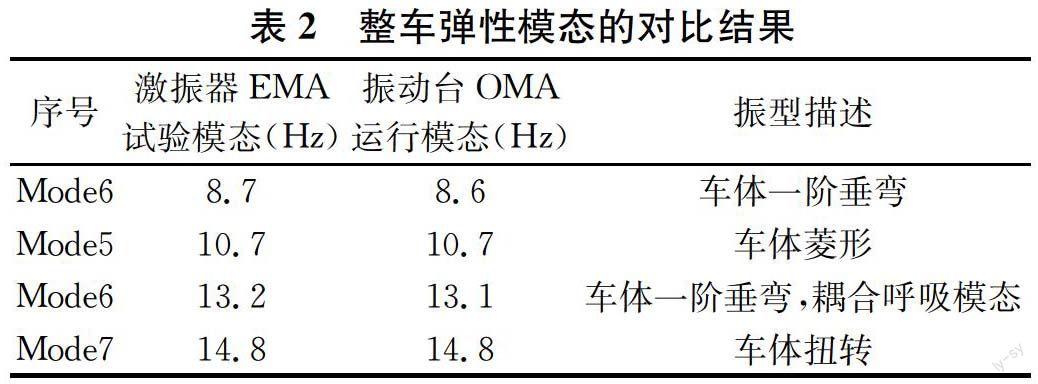
4.2 整车弹性模态的试验结果对比

图9-12为各阶模态振型的对比图，其中，左侧灰色背景为EMA试验方法下，PolyMax方法得到的模态结果，右侧白色背景为OMA试验方法下，FSDD方法得到的模态结果。

由上述结果可以看出：两种分析方法都出现了两个车体一阶垂弯阵型，通过进一步分析可知，导致出现两个垂弯模态的主要原因应该是车体中部的大质设备量变压器，而且采用的是弹性吊挂方式与车体连接，从原理上将，多一级质量与悬挂会导致运动微分方程多一级自由度，必然会增加一个解。

5 结论

通过两种试验方法及两种模态参数识别方法的比较，得到了基本一致的模态参数结果，相互验证表明结果真实可信。发现大质量物体采用弹性吊挂会导致车体出现额外的模态振型结果。

另外，激励能量和激励点的选择关系到试验结果的准确性，如果条件允许，更大的激励能量对激发各阶模态有益，直接激励各阶模态的振型节点位置也是很好的选择，激励带宽必须涵盖试图分析的频率范围。

经过这次的试验研究，积累了宝贵的模态分析经验，未后续产品的研发与设计提供支持。

参考文献

[1]王福天.车辆动力学[M].北京：中国铁道出版社，1998.

[2]宫岛，周劲松，孙文静等.高速列车车下设备模态匹配研究[J].振动与冲击，2014，33（8）：180185.

[3]周劲松，张洪，任利惠.模态参数在铁道车辆运行平稳性研究中的运用[J].同济大学学报，2008，36（3）：383386.

[4]任尊松，刘志明.高速动车组振动传递及频率分布规律[J].机械工程学报，2013，49（16）：17.