休闲观光农业创意折叠桌动态规律与加工参数设计研究
2016-05-30王一甲李志慧
王一甲 李志慧
摘 要:为改善休闲观光农业基础设施配置,以一种观光农业创意折叠桌为研究对象,从节约空间,提高美观特性及稳固性角度出发,对其进行动态规律及加工参数进行设计研究。根据折叠桌动态变化将其桌面简化为双曲抛曲面,运用空间几何分析求解出相应木条及开槽长度。通过多元回归分析推导出木条端点空间坐标间关系,应用Matlab软件对折叠过程中桌角边缘线进行拟合,确定最长木条长度为57.825cm,最长开槽长度为17.87cm。为提高其结构稳定性,进行静力学分析并对木材用料量进行优化,运用有限元分析验证优化结果。在此基础上求解出边缘线形状与桌面高度间关系,并推导其理论通用模型,以提高模型通用。
关键词:休闲观光农业;折叠桌;动态规律;加工参数;Matlab;ANSYS
休闲观光农业是一种以农业和农村为载体的新型生态旅游业[1-2],主要利用田园景观、自然生态及环境资源等通过规划设计和开发,结合农林牧渔生产、农业经营活动、农村文化及农家生活,提供人们休闲增进居民对农业和农村体验。此种形式的兴起和发展不仅是社会经济发展的必然趋势,也是推动人与自然、城市与农村和谐共存的不可替代的形式。国内外休闲观光农业的发展最初以“市民农园”为主,随着社会经济快速地发展,观光农业的观光、休闲功能不断得到强化,凭借大中城市资金、技术、市场、信息和人力资本集中的优势而发展起来的休闲观光农业园区,促进传统农业转向现代农业转型[3-4],解决农业发展的部分问题。
舒适温馨的环境是发展休闲观光农业的重要保证,而基础设施合理的空间配置,美学特性及力学稳固性是提高观光农业生活质量的重要因素。本文以一种观光农业创意折叠桌为研究载体,从节约空间,提高美观特性及稳固性角度出发,利用已知数据和条件,建立模型以描述此折叠桌的动态变化过程,确定其设计加工参数,在此基础上对折叠桌进行力学分析,对木材用料量进行优化以提高其结构稳定性,运用有限元分析检验优化结果。通过空间几何分析方法推导出折叠桌通用模型,应用Matlab软件对折叠桌动态变化进行数学描述。
图1 创意平板折叠桌动态变化过程
1 观光农业折叠桌结构及建模
如图1所示,此种为观光农业创意折叠桌其桌面呈圆形,桌腿由两组若干根木条构成,每组各用一根钢筋将木条连接,钢筋两端分别固定在桌腿各组最外侧的两根木条上,且沿木条有空槽以保证滑动的自由度,桌腿可随铰链的活动可以平摊成一张平板。折叠桌结构参数为:桌子平板尺寸为120cm×50cm×3cm,每根木条宽2.5cm,连接桌腿木条的钢筋固定在桌腿最外侧木条的中心位置,折叠后桌子的高度为53cm。
本文根据桌子外形曲面为直纹曲面的特点,简化设定该曲面为双曲抛物面[5-6]。在此基础上运用图形解析法得到各桌腿的长度,应用Matlab软件确定出各木条端点的坐标值。应用Spss软件分析各点坐标值,进行多元回归分析得出两个模型,根据相应数据对比两模型的合理性,以建立出正确的数学模型。
为简化应用模型,本文进行如下假设:平板折叠桌受力均匀,即物体在桌面上分布合理,忽略集中摆放情况;钢筋竖直(图中标红位置),即在折叠过程中不会产生变形而影响效果。(图2)
1.1 双曲抛物面 双曲面的形成的过程是:一直母线AC沿两交叉直导线AB、CD运动,同时始终平行于一导平面;它的两个导平面P、Q为铅垂面,其交线为铅垂线,平行于主轴Z;因两个导平面的等分角面分别为正平面和侧平面,故该曲面的两个对称平面S、U分别平行于正面和侧面。该曲面所处的位置为标准位置,如图3所示。
令坐标XOY和YOZ分别于曲面的两个对称面重合,过点O的铅垂线为曲面的主轴,点O为坐标原点,过点O垂直于侧面或正面的直线分别为Y轴或X轴。
令该曲面上的两个对称点A、D的x、y、z坐标分别为m、o、k,点B、C的x、y、z坐标为o、n、k,其中m、n、o、k为常数,于是得出双曲抛物面的标准方程:-+=0(1)
根据以上各端点坐标,利用Matlab软件编程[7-8]拟合出其三维曲线图形,如图6所示。
式中,y*为根据所有自变量计算的估计值,b0为常数项,b1、b2…bn称为y对应于x1、x2…xn的偏回归系数。偏回归系数表示假设在其他所有自变量不变的情况下,某一个自变量变化引起因变量变化的比率。
利用Spss对该数据进行多元线性回归分析[9]得到復相关系数R。其中复相关系数R是自变量与其他因变量间线性相关密切程度的指标,取值范围在0~1之间。其值越接近1,表示其线性关系越强;其值越接近零,表示线性关系越差。
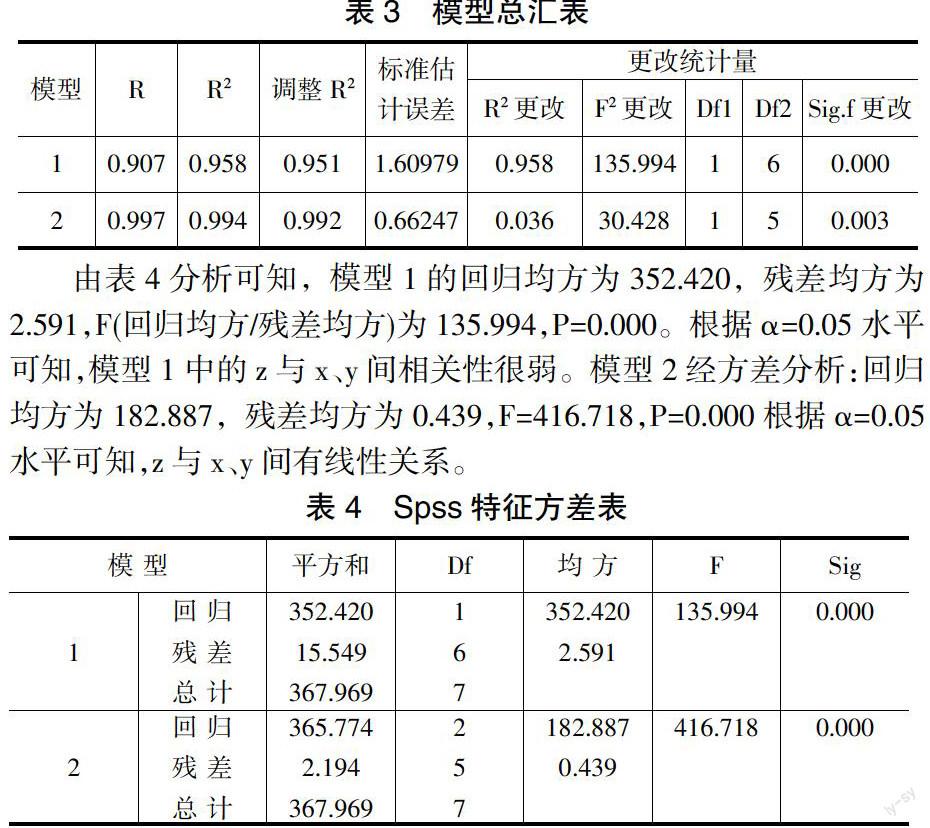
如表3所示,为显示各模型拟合情况。模型2的复相关系数(R)为0.997,判定系数(R square,即R2)为0.994,调整判定系数(Adjusted R square)为0.992,估计值的标准误差为0.6624767。模型1的复相关系数为0.797,判定系数为0.958,调整判定系数(Adjusted square)为0.951,估计值的标准误差为1.6097925。模型2的调整判定系数大于模型1的判定系数,说明两个因素的引入对方程的拟合程度的影响很大;且模型2的R2值大于模型1的R2值,故模型2的拟合度更高些。
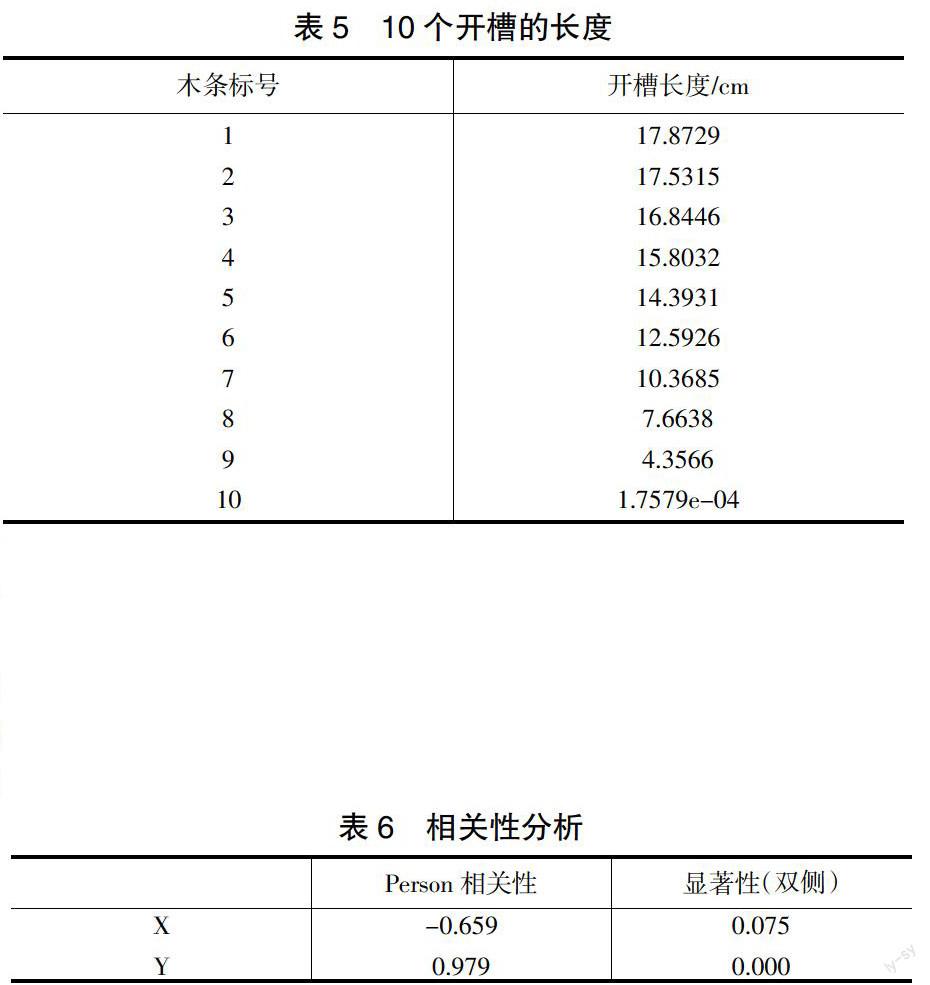
桌脚边缘线是由木条的端点构成的空间曲线,且随着木条的运动不断变化。因此曲线变化与桌腿的长度和开槽长度均有影响,所以本文研究的是在该情况下的最后位置的曲线描述,将讨论曲线上各点的z值分别被该点的x值和y值的影响程度。
利用Spss软件分别对z和x,z和y进行相关性分析,得出其Person相关系数为-0.659和0.979。检验方法为双侧显著性检验值为0.075和0.000在0.01的显著性水平上显著相关,所以可知在Z方向的变化其Y值影响较大,X值影响较小。其数据分析结果如表6所示:
2 观光农业折叠桌参数模型优化
观光农业折叠桌动态稳定性是评价其质量的重要指标之一,折叠桌钢筋位置和木条开槽长度是影响稳定性重要因素。钢筋在最长木条的中间位置是固定的,但在中间其他木条中是沿着开槽滑动的,因此在不同位置时最长木条处的钢筋所引导的其他木条运动的轨迹不同,即最后折叠成桌子的形状也将有所差异,随之影响桌子的受力情况。开槽长度的不同将导致由钢筋固定桌腿的位置和角度有所改变。本文采用逆向思维的方法,通过对不同设计参数的设定提高桌子的承重能力,研究钢筋的不同位置和开槽长度的范围,在此基础上采取优化设计出适宜的结构参数[10]。
2.1 稳定性分析 桌子稳定性主要由其钢筋位置及开槽长度决定。为便于加工且用料最少,本文在保证稳定性的前提下减少使用材料,选择最优加工参数。
根据力学知识可知,影响桌子结构稳定性的因素主要为重心位置高度和角度值(稳定角)大小。此稳定角为在三维空间结构重心到结构支撑面某支撑点的连线与此支撑点到重垂足(重心向结构支撑面引垂线得到的垂足)的连线所组成的夹角。
对折叠桌进行力学性能分析。为简化分析将桌子除支撑外所有木条以及对应的销钉去除,如图8所示。
此结构为多级超静定桁架,采取增加木条的方法增加其超静定次数, 降低受力敏感度,以提高结构稳定性。为尽可能减少摩擦力对其结构受力的影响,桌脚木条与水平面夹角应该有所限制。经工程实践证明,采用优良的结构形式,对抵抗较大幅度的超载、随机外力及避免脆性破坏或连续破坏均有十分重要的意义[11]。
经分析可知,当稳定角θ趋向于90°时,即桌脚与水平面垂直时,摩擦力对桌子结构的影响最小。但当若桌脚与水平面垂直时,其他木条均处于桌面下侧,并向里侧收缩,如图9所示。
销钉对桌脚木条将有很大作用力,并朝向外侧,对其力学性能有较大影响。因此对整体结构,桌脚与水平面夹角为90°并非最佳角度。
在此基础上通过增加木条数量来提高桌子的稳定性。在木条数量一定的前提下,假定中心木条到最外侧桌脚木条的角度变化量为恒定值,即它们与水平面的夹角是等差数列。
根据上述理论对圆形折叠桌进行分析,应用Matlab软件进行模型动态加工,检验其理论的合理性及准确性,如图12所示。
4 结论
①为改善休闲观光农业基础设施配置,以一种观光农业创意折叠桌为研究对象,从节约空间,提高美观特性及稳固性角度出发,进行理论研究及分析,根据桌面动态变化将折叠桌面简化为双曲抛曲面,运用空间几何分析求解出相应木条长度及开槽长度。运用多元回归分析推导出木条端点空间坐标间关系,应用Matlab软件进行对桌角边缘线进行拟合,模拟出折叠桌动态变化,确定其最长木条长度为57.825cm,最长开槽长度为17.87cm。
②对折叠桌进行静力学分析,对木材用料量进行优化以提高其结构稳定性,运用多目标优化方法,求解平板尺寸、钢筋位置和开槽长度间的关系函数,运用有限元法对优化后的折叠桌进行应力应变分析,应用ANSYS軟件进行模拟仿真,检验其理论合理性。最终确定其优化参数为:最长平板长164.75cm,最长开槽长度为20.85cm。
③为更大满足折叠桌设计要求,推广其模型通用性,运用空间几何分析方法进行相应作图解析,得出桌面边缘线形状与桌面高度间的关系,推导其理论通用模型,并应用Matlab软件进行相应的动态模拟仿真。
参考文献:
[1]方志权.论都市农业的基础特征、产生背景与功能[J].农业现代化研究,1999,20(5):281-285.
[2]王真,莫建林,等.休闲观光农业园区规划探讨[J].农机化研究,2006,24(3):11-13.
[3]刘国强,李友华.农业高新技术园区评价指标体系的研究[J].农业技术经济,2001,(3):24-27.
[4]沈悦林,徐四海.现代农业园区建设的评价考核研究[J].科技通报,1998,14(6):457-460.
[5]侯国勇.桁架式展开结构设计、分析及试验[D].杭州:浙江大学建筑工程学院,2008.
[6]殷国卓.空间可展结构的几何构成及力学分析[D].北京:北京交通大学土木建筑工程学院,2008.
[7]张森,张正亮,等.Matlab仿真技术与实例应用教程[M].北京:机械工业出版社,2004.
[8]苏金明,张莲花,刘波,等.Matlab工具箱应用[M].北京:电子工业出版社,2004.
[9]薛薇.SPSS统计分析方法及应用[M].北京:电子工业出版社,2009.
[10]哈尔滨工业大学理论力学教研室编.理论力学(I)[M].北京:高等教育出版社,2009.
[11]陈向阳,关富玲,陈务军,等.复杂剪式铰结构的几何分析和设计[J].空间结构,1998,4(1):45-51.
[12]王庆五,左昉,胡仁喜,等.ANSYS10.0机械设计高级应用实例[M].北京:机械工业出版社,2006.
