数学建模方法在“看病难、看病贵”问题中的应用

2016-05-30刘红江

中小企业管理与科技·下旬刊 2016年2期

刘红江

摘要：“看病难、看病贵”是当前中国面临的一个重要的问题，仅次于“收入问题”。虽然国家采取了措施进行医疗制度改革，但医疗保障制度仍存在不少问题，有些问题还非常严重，甚至到了制约经济体制的发展。改革医疗制度是关系人民群众切身利益的重要问题，也是构建和谐社会的重要问题。本文通过运用数学建模知识说明城市居民和农村居民就医难的难易程度，并给出改革医疗制度的建议。

关键词：医疗制度；层次分析法；矩阵；组合权重

1 看病难问题的提出

“看病难、看病贵”是当前我国存在的一个问题。2012年4月18日国务院办公厅发布了关于《深化医药卫生体制改革2012年主要工作安排》的通知，其中有三个方面重要改革：①加快健全全民医保体系；②改革医保支付制度，深化基层医疗卫生机构综合改革；③积极推进公立医院改革，拓展深化城市公里医院改革试点。

2 看病难问题的原因分析

①医疗资源总量不足，卫生发展落后于经济发展；②医疗资源分布失衡，医疗服务的社会公平性差；③医疗卫生筹资机制改革滞后，多数老百姓自费就医；④国家政策调整或新的行业就范，增加了病人的医疗负担；⑤社会医疗保障体系不健全，覆盖面太小。⑥群众对医疗卫生服务的需求不断增长；⑦医疗机构市场主导，片面追求经济利益。

通过以上分析，将看病难总结为四类：

①各种疾病治疗措施；②疗养休养措施；③诊疗检查费；④相应药品消耗。

针对问题，我们给出相关数据（假设数据真实可靠），建立评价模型，采取层次分析法客观评价城市和农村看病就医的难易程度。

3 看病难问题的求解

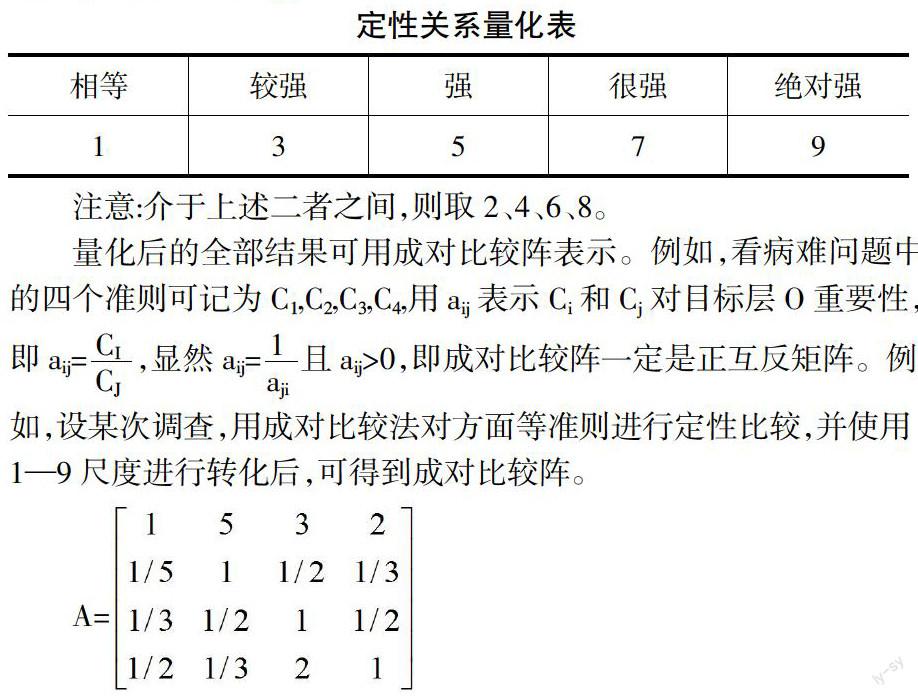
建立成对比较阵构造-定性向定量的转换，使用尺度1-9对定性关系进行量化，具体下表：

注意：介于上述二者之间，则取2、4、6、8。

量化后的全部结果可用成对比较阵表示。例如，看病难问题中的四个准则可记为C1，C2，C3，C4，用aij表示Ci和Cj對目标层O重要性，即aij=，显然aij=且aij>0，即成对比较阵一定是正互反矩阵。例如，设某次调查，用成对比较法对方面等准则进行定性比较，并使用1—9尺度进行转化后，可得到成对比较阵。

A中A12=5表示各种疾病治疗措施C1与疗养休养措施C2对看病难这个目标O的重要性之比为5：1。

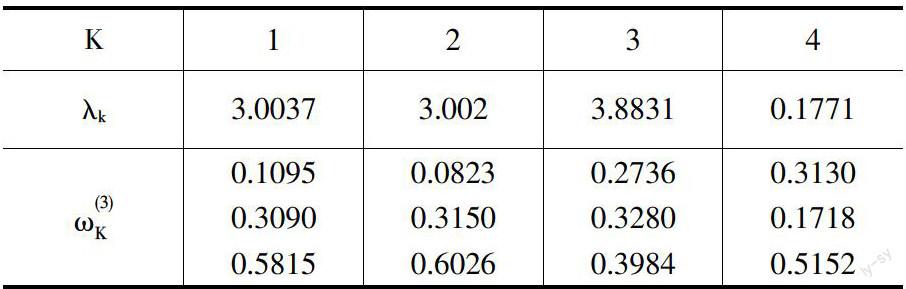
下面计算权向量：

同理，城镇医院的权重为0.2810，城市医院的权重是0.5437，通过计算结果显示：农村看病难，城市看病容易。

4 结论与建议

通过上面的求解可知，城市医院占的权重比较大，农村医院权重相对低。这说明现有的医疗体制分配不合理，需要进行改革。同时随着中国经济的发展，这个问题显得更为突出，国家需着手解决人民看病难问题。

建议：

①社会监督——对医生事后评价制度。对医生和医院根据评价制度给予拨款。对于特殊医院由政府给予支助和行政支持。

②行政管理——成立独立的稽查单位，由省级以上的卫生厅管理。管理单位每年都要例行检查，对出现问题的医院进行处理，确保群众的利益。

③参加医保的人员在看病时有必要保密医保信息，同时加大药物的报销力度。

④建立非营利医院，切实为人民服务。

5 结束语

综上所述，我们可以看出，看病难是当前我们面临的一个重要问题，只有将群众利益和医院效益结合起来考虑，才能建立比较合理的医疗制度体系，才能实现人们的健康和谐生活，才能使国家安定和谐发展。