材料力学剪力图与弯矩图的简易绘制方法

师艳景

摘 要：本文以剪力、弯矩和分布荷载集度之间的微分关系为基础，求出支座反力后可快速绘制剪力图，根据剪力图的正负和剪力图面积来绘制弯矩图。对于基础普遍较差的三本院校学生来讲，较易掌握。

关键词：微分关系；剪力图；弯矩图；剪力图正负与面积

中图分类号：TB121文献标志码：A文章编号：2095-9214（2016）09-0137-02

材料力学中弯曲变形是四种基本变形之一，剪力和弯矩为弯曲变形的内力。剪力图和弯矩图的绘制，可以很方便的看到梁各个横截面上的剪力弯矩数值大小和正负，从而确定出梁的危险截面，为后面的正应力强度校核和切应力强度校核做准备。

一般教材中介绍的剪力图弯矩图的绘制有两种做法。第一种是先列出剪力方程和弯矩方程，根据方程作图。很显然，如果梁上受到荷载种类较多时，剪力方程和弯矩方程需分很多段来列，非常复杂，因此这种做法用的较少。第二种方法是基于剪力、弯矩和荷载之间的微分关系来绘制。这种方法通常是在梁上取若干控制截面，直接由外力计算出控制截面上的剪力值和弯矩值，再根据微分关系确定两控制截面之间的剪力图和弯矩图的连线。这种方法较第一种简便，对于一些成绩好的同学也可以掌握。

但是，如果梁上外荷载较多，所选取控制截面也会较多，计算较为复杂。此外，对于有一些基础较差的同学，由外力计算剪力弯矩值掌握较吃力。故本文在剪力、弯矩和荷载集度微分关系的基础上提出一种剪力图、弯矩图的简易绘制方法，供广大读者参考。

一、绘制依据

1.剪力与荷载集度之间的关系dFs（x）dx=q（x）。由该式可得，dFs（x）=q（x）dx。即某段梁上剪力的增量，等于荷载图的面积。

2.弯矩与剪力之间的关系dM（x）dx=Fs（x）。由该式可得，dM（x）=Fs（x）dx。即某段梁上弯矩的增量，等于剪力图的面积。

二、绘制方法

（一）求解支座反力

由静力学平衡方程求出支座反力，不再赘述。

（二）剪力图绘制

从左到右绘制剪力图：

①剪力初始值为零。

②若梁上有向上（下）集中力（含支座反力）作用，则剪力图向上（下）突变，突变值等于集中力的大小。

③若梁上有向上（下）均布荷载作用，则该段梁上剪力图为斜向上（下）的直线，剪力的增量为该段梁上分布荷载的面积。

④若梁上有集中力偶（含支座反力）作用，剪力图没有变化。

⑤若梁上无荷载，则剪力图为水平直线。

⑥检查梁末端截面的剪力值是否归于零。如不是零，则说明中间过程有误，需检查修改。

（三）弯矩图绘制

①综合荷载图和剪力图，从左到右绘制弯矩图。

②弯矩初始值为零。

③从左到右，若梁上有集中力偶（含支座反力）作用，则弯矩图有突变。突变值等于集中力偶大小。若集中力偶顺时针，则弯矩图往正向即向下突变；反之，若集中力偶逆时针，则弯矩图往负向即向上突变。

④若梁上有向上（下）均布荷载作用，则弯矩图为向上（下）凸的抛物线。该段梁上弯矩的增量为对应梁段剪力图的面积。若剪力图为正，则弯矩增量为正；若剪力图为负，则弯矩增量为负。

⑤若梁上无荷载，则弯矩图为斜直线。该段梁上弯矩的增量为对应梁段剪力图的面积。若剪力图为正，则弯矩增量为正，弯矩图为斜向下直线；若剪力图为负，则弯矩增量为负，弯矩图为斜向上的直线。

⑥若梁上有集中荷载，则弯矩图在集中荷载作用处有尖角。

⑦检查梁末端的弯矩值是否归于零。如不是零，则说明中间过程有误，需检查修改。

三、举例

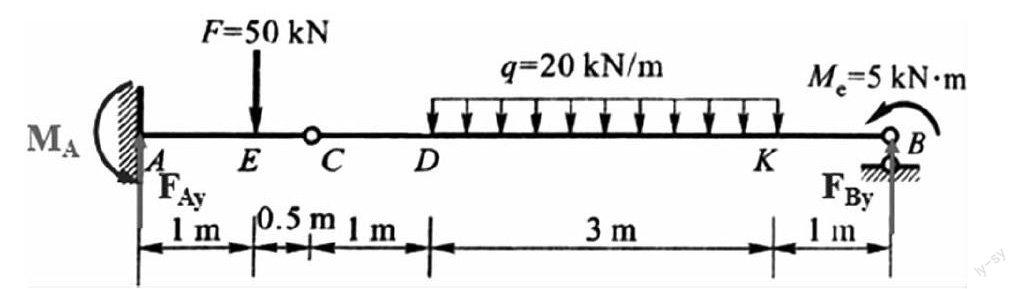
图中所示具有中间铰C的静定梁，试绘制剪力图和弯矩图。

（一）由静力学平衡方程求解支座反力得

FAx=0FAy=81kNFBy=29kNMA=96.5kN·m

（二）绘制剪力图

从左到右绘制剪力图，剪力初始值为零；

A截面有向上的集中力FAy（支座反力），故剪力图向上突变，突变值等于FAy等于81kN，突变后剪力变为81kN；

从A右截面至E左截面梁上无荷载作用，故剪力图为水平直线；E截面有向下的集中力F=50kN，故剪力图向下突变，突变值等于F等于50kN，突变后剪力值变为31kN；

E右截面至D左截面梁上无荷载作用，故剪力图为水平直线；

D截面至K截面梁上为向下的均布荷载，故剪力图为向下倾斜的直线，该段梁上剪力值的增量为荷载图面积，即-20×3=-60kN，故K截面的剪力值为31+（-60）=-29kN；

K右截面至B左截面梁上无荷载，故剪力图为水平直线；

B截面有逆时针的集中力偶，但不影响剪力图，故剪力图无变化；

另外B截面处还有向上的集中力FBy（支座反力），故剪力图向上突变，突变值等于FBy等于29kN；

最终剪力图回到零点。

（三）绘制弯矩图

从左向右绘制弯矩图，弯矩初始值为零。

A截面有逆时针集中力偶MA（支座反力），由前文所述规律，弯矩图往负向即向上突变，且突变值等于集中力偶等于96.5kN·m。突变后，弯矩值变为了-96.5 kN·m。

A右截面至E左截面，梁上无荷载作用，弯矩图为斜直线。由于该段梁上剪力图为正，故弯矩值逐渐增加，即弯矩图为斜向下直线。弯矩的增量为剪力图的面积，即81×1=81 kN·m，至E左截面，弯矩值变为-96.5+81=-15.5 kN·m。

E截面有集中力作用，弯矩图会有尖角（弯矩图绘制完成后可看到）。

E右截面至D左截面，梁上无荷载作用，弯矩图为斜直线。且该段梁上剪力图为正，故弯矩值逐渐增加，即弯矩图为斜向下直线。弯矩的增量为剪力图的面积，即31×1.5=46.5kN·m，至D左截面，弯矩值变为-15.5+46.5=31 kN·m。

D截面至K截面，梁上有向下的均布荷载作用，弯矩图为向下凸的抛物线。且由剪力图可看到，在距离K点1.45m的H点处剪力为零，则该点处弯矩有极值。D右至H段梁弯矩增量为剪力图面积，即31×1.55÷2=24 kN·m，故H截面弯矩值为31+24=55 kN·m。HK段梁弯矩值增量为-29×1.45÷2=-21 kN·m，故K截面弯矩值为55+（-21）=34 kN·m。

K右截面至B左截面，梁上无荷载作用，剪力图为负，故弯矩图为斜向上直线。弯矩增量为-29×1=29 kN·m，则B左截面弯矩值为34+（-29）=5 kN·m。

B截面处有逆时针集中力偶Me，则弯矩图往负向即向上突变。突变值等于集中力偶大小等于5 kN·m，突变后，弯矩值归于零，可认为弯矩图绘制正确。

对于本题来讲，有中间铰C，画完弯矩图后需检查在此处弯矩值为零。

四、总结

本文提出的方法以弯矩、剪力与荷载集度微分关系为基础，求出梁的支座反力以后无需进行繁琐的剪力方程、弯矩方程计算，也无需依外力计算各控制截面剪力弯矩数值，而通过计算简单的几何图形面积辅以基本规律就可绘制剪力弯矩图。作者认为，该种方法简易方便，对基础较差的三本学生较易掌握，对基础好的学生则可以帮助其快速准确的绘制剪力弯矩图。

（作者单位：天津大学仁爱学院）

参考文献：

[1]孙训方，方孝淑，关来泰.材料力学（Ⅰ）[M].北京：高等教育出版社，2009.