基于概率距离的电脑鼠迷宫搜索算法

王磊　董珊　潘洪友

摘 要：效率不高是目前电脑鼠竞赛中迷宫搜索算法存在的普遍问题，为此，提出一种基于概率距离的电脑鼠迷宫搜索算法。通过生成静态概率距离图，并结合对迷宫图的动态处理，以达到提高迷宫搜索效率，缩短迷宫搜索时间的目的。测试结果表明，基于概率距离的电脑鼠迷宫搜索算法，在迷宫搜索效率、迷宫搜索时间等方面，较左手、中左、中心、中心分区算法有明显优势。

关键词：迷宫搜索算法 电脑鼠 迷宫 概率距离 封闭体算法 搜索效率

中图分类号：TP242.6 文献标识码：A 文章编号：1674-098X（2016）01（c）-0093-03

Abstract：Low efficiency is the regular problem in search algorithm of Micromouse maze at present. To solve this problem， proposed the search algorithm based on probability distance. This algorithm creates a static probability distance map， and combines the dynamic handling of the maze map to improve the efficiency and speed of maze search.The results show that search algorithm based on probability distance of Micromouse maze has a big advantage of search efficiency and search time comparing with the left hand， center left， center， center partition algorithm.

Key Words：Maze search algorithm；Micromouse；Maze；Probability distance；Closed body algorithm；Search efficiency

电脑鼠（Micromouse）是使用嵌入式微控制器、传感器和机电运动部件构成的一种智能行走装置（微型机器人），电脑鼠可以在不同“迷宫”中自动记忆和选择路径，采用相应的算法，快速地达到所设定的目的地。电脑鼠竞赛的迷宫[1]由256个迷宫格组成，每个迷宫格的大小为18 cm見方，排成16行16列。电脑鼠走迷宫竞赛的目的是设计制作一个电脑鼠，按照规则要求以最快的速度完成比赛。

迷宫搜索过程中，电脑鼠除去需要正常记录迷宫格信息、自身所在位置、方向等数据，还需要使用某些迷宫搜索算法，进行行进路线的抉择[2]，该过程属于机器人路径规划的范畴，是基于地图未知的路径规划方法在电脑鼠走迷宫竞赛中的具体运用。当前使用的迷宫搜索算法有很多，常见的主要有以下几种。

（1）左手/右手法则[3]，当电脑鼠行进中遇到两条或更多的支路时，优先考虑向左/右行进，其次考虑向前，最后才考虑向右/左行进；（2）中左/中右法则，优先考虑前行，其次考虑向左/右行进，最后才考虑向右/左行进；（3）求心法则，优先选择离中心点最近的方向行进，同时有两个离中心最近的方向供选择时，选择直线方向；（4）中心分割法则[4]，将迷宫分为几个部分，根据每个部分相对于目标区域的位置和当前电脑鼠行进的绝对方向，采用不同的法则来控制电脑鼠运行。

以上几种迷宫搜索算法普遍存在搜索效率不高、搜索时间过长的问题。为此，文章提出基于概率距离的电脑鼠迷宫搜索算法。

1 概率距离算法

概率距离算法，是一种通过生成静态概率距离图，并在电脑鼠运行过程中对迷宫图进行动态处理，来辅助电脑鼠进行路径抉择的算法。

1.1 静态概率距离图生成

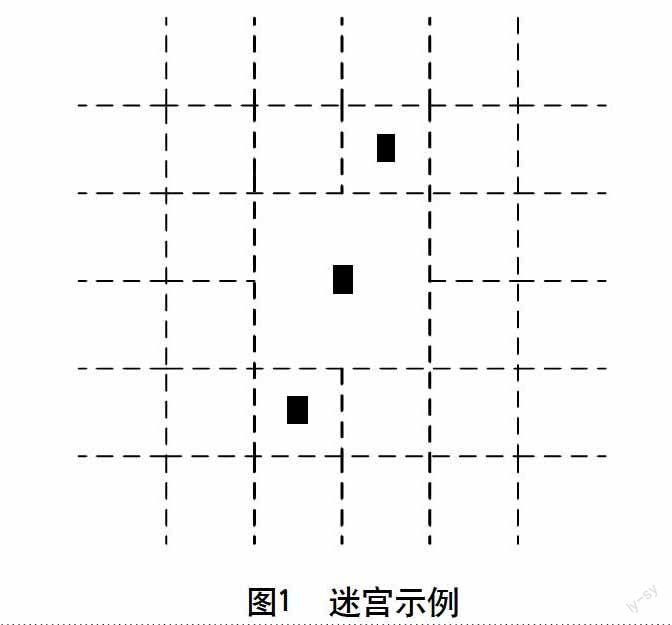
目标区域为迷宫中心的4个相通的迷宫格，此目标区域同外界相邻的是8个迷宫格，按照规则，目标区域必须与外界相通，也即目标区域G周围至多有7堵墙壁，如图1中所示，虚线表示可能存在的墙壁，虚线围成的方格为迷宫格。

假设初始时其他墙壁均不存在，单元格之间距离记为1，每一个90°转弯所耗时间也等效为距离，记为，每一个180°转弯所耗时间等效为距离b（测试中所使用的电脑鼠a≈1，b≈10）。

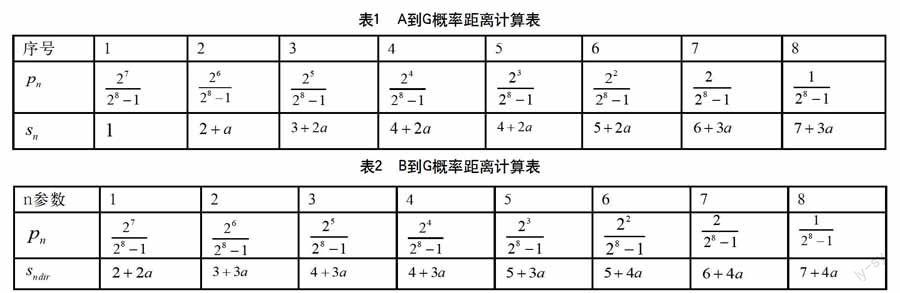
图1中迷宫格A和目标区域G的距离应该这样计算：距离A最近的墙壁不存在的概率为（28-1），A到G的最短距离为，即A到G有的可能距离为；在该墙壁存在的情况下，距离A第二近的墙壁不存在的概率·26/（27-1），此时A到G的最短距离为，即A到G有的可能最短距离为；依此类推，、如表1所示。

最终可得到A到G的距离：

由于上述结果是一个概率与距离的乘积，表示概率意义上的距离，所以也称其为“概率距离”。

上述概率距离的计算过程中，并没有考虑电脑鼠当前的方向，这显然是不合理的，因为每个转弯或调头，都会影响电脑鼠与目标区域之间的概率距离，所以电脑鼠当前的方向也是影响概率距离的因素之一。以图1为例，假设电脑鼠初始方向向上，B到G有的可能最短距离为；有的可能最短距离为；依次类推可以得到、如表2所示。

可得到B到G的有向概率距离：

根据迷宫单元格的物理位置进行分类并编号，并按照上述算法进行计算，可以得出迷宫中每个单元格到目标区域的概率距离，这样便可以生成一个方向为上的静态概率距离图，如图2所示。

同理，其他3个方向的有向概率距离图，可以由图2旋转得到，在此不再赘述。

1.2 迷宫图的动态处理

随着电脑鼠的搜索，越来越多的迷宫格数据被获取，根据获取的数据，使用封闭体算法（Closed body algorithm）对静态概率距离图进行修正。封闭体，就是在迷宫搜索过程中经常碰到的“死胡同”，是指某一区域与外界只有一个出入口连接，除非目标点在这一区域内，否则，进入该区域是不可能到达目标点的。封闭体算法主要由以下两个步骤实现。

1.2.1 迷宫格封闭

在电脑鼠搜索过程中，每探明一个迷宫格的墙壁数据，更新相邻迷宫格的墙壁资料，此时对墙壁资料有变动的迷宫格进行判断，若3个方向均为有墙，则对该迷宫格进行封闭[5]，即设置第4个方向为有墙；变更后继续对有墙壁数据更新的迷宫格进行同样的判断、操作，直至更新完毕。

1.2.2 迷宫区域封闭

在电脑鼠搜索过程中，遇到路口或要返回某个路口时，可以参考Flood-Fill[6]算法来进行判断：向该路口的某个方向相邻迷宫格注入某个数值，按照广度优先算法[7]，将此数值赋给所有连通的迷宫格（已探明的迷宫格除外），最终判断目标迷宫格是否也得到了这个值。若得到了，则路口的该方向是个可行路径，否则，判断为该方向不可行。

2 基于概率距离的迷宫搜索流程

基于概率距离的迷宫搜索，首先建立静态概率距离图，电脑鼠从起点出发后，使用“死路”算法更新迷宫格墙壁状态。若遇到路口，则使用Flood-Fill算法判断路口与终点是否存在可达性，若不存在，则关闭此方向的墙壁；若存在多个可行的方向，则利用静态概率距离图判断最优路径，直到电脑鼠到达目标区域。

3 测试结果

随机采用电脑鼠竞赛地图对“概率距离”算法进行测试，并使用“左手”“中左”“向心”“中心分割”等算法进行对比测试。结果如表3所示，“路程”表示行进距离，“总路程”表示90°转弯、180°转弯量化为路程之后的总和，“探明”表示搜索后已知单元格的总数，“效率”表示探明单元格数量与路程总和的比值。对于测试使用的地图，基于概率距离的迷宫搜索算法，在迷宫搜索效率、迷宫搜索时间（总路程）等方面，較左手、中左、中心、分区中心等搜索算法有明显优势。

4 结语

对于一个完全未知的迷宫，如何进行高效率的搜索，是电脑鼠走迷宫竞赛中的关键环节。文章提出了基于概率距离的迷宫搜索算法，从概率学的角度出发生成概率距离图，并结合电脑鼠运行过程中所获取的数据，形成了独特的搜索路径选择机制。这是一种迷宫搜索的新方法，测试结果表明其具有独特的优势。

参考文献

[1] MicroMouseInfo.com.Design of a working MicroMouse[EB/OL].[2015-12-27].http：//www.micromouseinfo.com/.

[2] 林国恩.电脑鼠的设计与制作[D].桃园：台湾龙华科技大学，2010.

[3] Mishra S，Bande P.Maze solving algorithms for micro mouse[C]//Signal Image Technology and Internet Based Systems， 2008. SITIS'08. IEEE International Conference on. IEEE， 2008： 86-93.

[4] 周立功.IEEE电脑鼠开发指南-基于MicroMouse615迷宫智能鼠[M].广州：广州致远电子有限公司，2010.

[5] Li X， Jia X， Xu X， et al.An improved algorithm of the exploring process in Micromouse Competition[C]//Intelligent Computing and Intelligent Systems （ICIS）， 2010 IEEE International Conference on. IEEE， 2010， 2：324-328.

[6] Mishra S， Bande P.Maze solving algorithms for micro mouse[C]//Signal Image Technology and Internet Based Systems， 2008. SITIS08. IEEE International Conference on. IEEE， 2008： 86-93.

[7] 严蔚敏.数据结构（C语言版）[M].北京：清华大学出版社，2007.