国际市场恐慌情绪传染分析与风险预警

刘思跃　梁鉴标

摘要：市场情绪是影响市场走向的重要因素。为了考察多个市场中恐慌情绪的联动问题，本文采用半参数的时变藤Copula函数对多市场情绪的联动结构进行刻画，并利用支持向量机为其估计变量的边缘密度函数，构建不依赖模型与分布假设的SVM- Dynamic Vine Copula系统；以美国、韩国、香港三个市场的VIX恐慌指数为研究对象的实证发现，三个市场间的相依结构存在显明的时变效应，且当前市场相依结构与次贷危机前期非常相似，作为预警信息值得关注；此外，压力测试发现，市场反应存在不对称性，美国市场更容易受香港市场的影响。

关键词：VIX指数；时变藤copula；半参数；支持向量机；恐慌情绪

中图分类号：F83文献标识码：A

2015年6月7日以来，我国A股开始了一轮又一轮大跌，为了守住防止系统性风险的底线，监管层、国家队纷纷护盘救市，随后千股涨停，千股跌停接连发生。8月24日沪指更是创了8年来最大单日跌幅。不仅是我国的A股市场，美股、欧股、亚太股市等全球市场也跌声一片，多个市场上都出了股市开始崩盘的忧虑，市场恐慌情绪开始蔓延。此时，美国恐慌指数（VIX）已经长期处于低位，这预示着恐慌指数有很大的上升可能，看跌情绪高涨。6月26日，上海证券交易所发布了中国首只基于真实期权交易数据的波动率指数——中国波指（iVIX）， 用于衡量上证50ETF未来30日的预期波动，反映投资者的情绪。VIX指数越高，表明投资者对后市的看跌恐慌情绪高涨，避险需求强烈，反之投资者对市场乐观。鉴于VIX指数的作用，本文以VIX指数作为市场恐慌情绪的度量，对市场间恐慌情绪的高维非线性联动结构进行建模，通过考察现在与历史的相依结构，为政府部门与金融机构研判与风险预警、进行宏观决策提供有效的参考。

一、文献综述

对金融变量间的联动或相关性进行刻画对度量风险与风险管理、构建投资组合、波动溢出效应研究有重要应用。目前对变量间联动相关特征进行研究的方法主要有简单的相关系数法、基于向量自回归的协整检验Granger检验、以GARCH模型为基础的DCC-GARCH模型，以及Copula函数等。以上方法大部分以二元变量间的相关性入手，忽略了多个市场下的共同作用。虽然Copula函数可扩展到多元的情形，但这假设了变量间具有相同的相依结构且用同一个函数进行表达。

为解决多元变量间相关性的问题，Bedford和Cook（2002）提出了按特定的“藤”层叠结构，将一高维Copula函数分解成一系列成对的二元Copula函数，每对二元Copula函数捕捉相应变量的相关结构。由于二元Copula函数研究相对成熟，种类众多，能够刻画不同不对称的尾部特征，这使得藤Copula函数在刻画多元变量间联动结构时有很好灵活性并得到广泛的应用。Aas等（2009）作出藤Copula函数相应的统计推断并将其应用到金融领域。Heinen等（2008）提出C藤自回归模型并将其应用到95只S&P500股票，发现该模型可近似看做CAPM模型的非线性版本且能很好地预测VaR。Brechmann等（2013）对Stoxx 50中重要股票运用藤Copula、DCC-GARCH、t-copula模型进行比对，发现藤Copula表现优于其它两个模型。范国斌等（2013）利用C藤Copula对上海、香港、台湾三个股票市场建模发现，C藤Copula比传统多元Copula更灵活地描述市场间的尾部相关性。杜子平等（2013）发现混合D藤Copula能更好描述资产组合的相关结构。Maya等（2015）利用R藤copula研究了拉丁美洲六个国家外汇风险传染水平，结果发现巴西、哥伦比亚、智利和墨西哥与其它国家表现为更强的相关性，并存在不对称性。

以上文献的藤Copula函数参数为常数，然而现实中变量间的相依结构往往是时变的。Patton（2006）提出运用类似ARMA（1，10）的过程描述二元正态Copula函数参数的时变过程。其它对二元Copula函数时变参数的方法还包括DCC Copulas、随机自回归Copulas（SCAR）、结构断点、区制转换copuals（RSC）等。但以上方法中假设参数服从于确定的演化方程。Hafner and Reznikova（2010）认为设定演化方程可能给建模带来偏差，應将参数视为关于时间变化的未知函数，由此提出了通过半参数技术对Copula参数进行建模。以上方法主要应用在成熟的二元Copula函数中。目前国内外对时变藤Copula函数的研究并不多见。本文借助Hafner的思想，以半参数的方法构建时变参数的藤copula函数。

传统的Copula函数步骤中，首先对边缘分布作出假设（常用高斯分布或者t分布），然后选择适当的Copula函数对相关结构进行刻画，从而可灵活地得到联合分布函数。但实际应用中，计量模型的假设往往与数据不符，严格的分布假定可能会忽略数据重要信息。为了充分利信息，本文利用机器学习中的支持向量机技术，不对变量作任何分布假设，以数据驱动拟合变量的密度函数。结合支持向量机与半参数时变藤Copula函数，本文构建SVM- Dynamic Vine Copula半参数系统对多个市场间的恐慌情绪进行分析，深度挖掘恐慌情绪相依结构信息。这也是本文的主要贡献所在。

二、半参数建模方法

（一）基于支持向量机的概率密度估计

支持向量机（support vector machine）是通过结构化风险最小来提高泛化能力，以有效解决小样本、非线性、高维模式识别问题的一种机器学习方法，广泛应用在分类及回归分析中。

这使得在不研究边缘分布的情况下，也可以用Copula函数研究变量间的相关性，同时也为求得联合分布提供了简便方法。变量间的相关结构完全由Copula函数刻画，选择适当的Copula函数是模型构建的关键。目前应用已经十分成熟的是二元结构的Copula函数，常用的Copula包括椭圆类Copula、Gaussian和Student t Copula，但它们只能刻画对称的相关结构，且Gaussian Copula无法捕捉尾部相关性，Student t Copula只能捕捉对称的尾部相关性，而实际市场上广泛存在非对称相关结构，因而具有一定缺陷。另一类Copula函数是Archimedean Copula，常见有捕捉非对称结构，刻画上尾相关的Gumbel Copula，刻画下尾相关的Clayton Copula，以及描述变量负相关关系的Frank Copula等。

其中尾部相依系数广泛应用在极值理论中，可以很好地刻画变量的非对称极端风险事件。上尾相依系数越大，表明一个变量地急剧上升引起另一个变量同样方向变动的概率也会增大，下尾相依系数反之。Joe（1997）给出了Copula函数参数与尾部相依系数的关系定义。本文实证部分用到的Copula函数分别为Gumble、Joe、Clayton，其尾部相依系数与参数关系分别为：

当关注高维变量时，Copula的选择相对有限，常用的三元Copula有Gaussian、Student t和Clayton，但是这些多元Copula假设变量间具有相同的相依结构，用同样的Copula函数进行表达，与实际不符。

为解决多元变量间相关性的问题，Bedford和Cook（2002）提出“藤”Copula。根据不同分解方法，常用的藤结构有drawable vine（D藤） 和canonical vine（C藤） copulas。若存在一个变量与其它变量的相关性明显高于其它，则选用C藤；若变量间的相关性接近，则采用D藤。图1为4维C藤和D藤结构的展示。

对应于图1中的C藤，一般地，多元联合密度函数有如下分解：

三、实证研究与结果分析

（一）数据来源与统计描述

由于中国波指在6月26日试运营，而标的50ETF期权上市时间尚短，目前数据不多，未公开下载，所以本文选取美国芝加哥期权交易所CBOE VIX指数、韩国VKOSPI200指数、香港恒指波幅指数。后两者与前者编制方法一致，只是相应的股指期权标的不同。数据分别来源芝加哥期权交易所、韩国证券交易所、wind资讯金融终端。由于CBOE VIX指数2003年经过重新编制且只提供2004年以来数据，所以实证样本时间跨度为2004年1月2日到2015年9月8日，取三個市场共有交易日，共2 728组数据。

表1给出各国/地区VIX序列的描述性统计结果。由表1可以看出：香港与韩国的恐慌指数均值高于美国，而美国与韩国的标准差低于香港，反映香港和韩国市场的恐慌情绪相对较高且前者的波动更大，这在某种程度上说明美国投资者对自身国家股票市场的信心较足。三个指数序列偏度均不为0，峰度均不为3且明显偏离3，说明指数序列具有明显的尖峰厚尾分布的特征。JB统计量在1%的显著性水平下拒绝服从正态分布的原假设，说明恐慌指数序列不能用简单正态分布建模。

利用支持向量机对边缘分布进行拟合，充分保留了数据原有的尖峰厚尾特征以及其它分布信息，避免了由于错误假设而引起Copula函数的错误选择，得到更加准确的相关结构的刻画。构建Copula模型首先要对边缘分布进行Ljung-Box检验，检验模型假设的正确性。这里采用半参数方法即支持向量机对边缘分布进行刻画，并不涉及分布假定。其次要对变换后的概率分布序列进行Kolmogorov-Smirnov检验，检验变换后的序列是否服从[0，1]上的均匀分布。由KS检验，三个序列均在5%的显著性水平上通过检验。

由相关系数矩阵可知，香港的恒指波幅指数与其他变量间的相关性明显高于其他变量，由此采用C藤结构。以香港恐慌指数作为中枢变量，首先选择适合的Copula函数刻画香港与美国、韩国的无条件相关结构，然后以香港恐慌指数为条件，刻画美国与韩国的条件相关结构。

（二）常系数与变系数藤Copula模型的构建

在进行藤Copula建模时，不可避免地涉及不同节点Copula函数的选择问题。不同的Copula函数对相关结构的刻画能力并不相同，对Copula函数错误的选择将造成相关结构的误判。根据Aas等（2009）关于不同节点上函数选择的建议：首先对T1层各变量，通过观察两两之间的散点图，选择可能的Copula函数并进行无条件系数估计；然后由T1层系数估计结果，根据（14）式，计算T2层各变量的条件分布函数值，同样再次通过观察各变量所对应的条件分布散点图，选择可能Copula函数；此后各层以此类推。对于所有可能的选择，可通过参数估计后的AIC、BIC进一步优选。

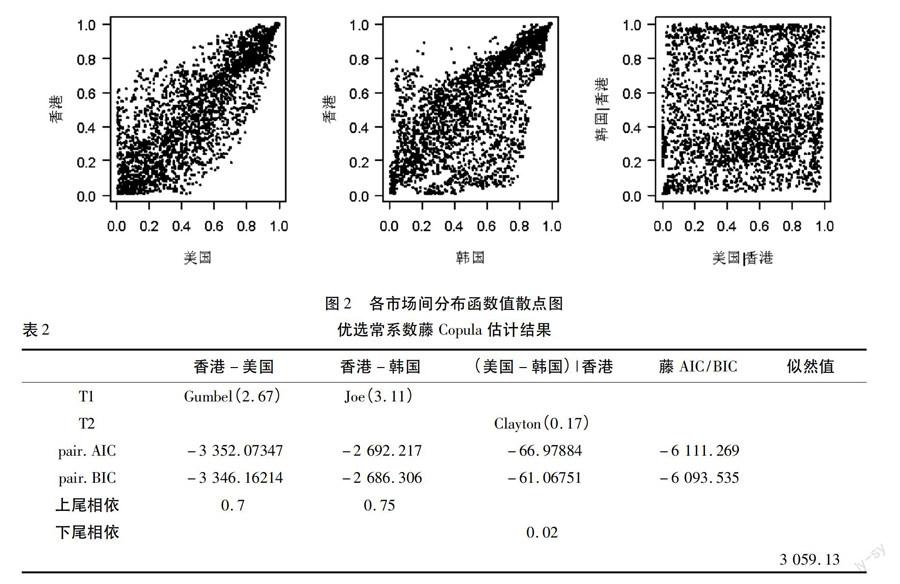
由图2，可以看到香港与美国、香港与韩国间的恐慌指数均为正相关，且存在较明显的上尾相关特征，相关结构存在一定的不对称性，其中香港与韩国两个变量的不对称相关特征更为明显。由此可知，关于T1层的Copula函数可以排除椭圆类的Gaussian、Gaussian和Student t Copula，而可刻画上尾相关的常用Archimedean Copula、Gumble以及Joe等。T2层的条件分布散点图并无明显可分辨特征，因此可基于AIC及BIC准则寻找更合理的Copula函数。从常用Archimedean Copula及椭圆类Copula类中，表2给出基于AIC、BIC准则的优选Copula函数及相应藤Copula参数的估计结果。

由表2可见，在T1层，香港与美国，香港与韩国间的相关结构分别由Gumbel、Joe Copula函数刻画，这与图2初步观察相符，其相关参数分别为267和311，对应上尾相依系数为07和075。这表明香港与美国、韩国间的恐慌情绪存在显明的上尾正相关结构，即一个地区对市场悲观情绪的迅速上升，另一个地区市场恐慌情绪出现的可能明显增大。T2层的优选Copula函数为Clayton，表明以香港恐慌指数为条件，美国与韩国的条件相关结构存在下尾相关性，相关参数为017，下尾相依系数为002。这暗含着在已知香港市场情绪的条件下，韩国与美国间存在一定的下尾相依，但不是特别显明，至少不独立，即在香港市场乐观时，美国与韩国的乐观预期存在一定的相互影响。

以上常系数藤Copula估计给出了2004年1月2日以来三个市场间的相依结构关系，但是现实中相依结构往往是变化的，在不同时期表现出不同的关系。基于半参数的藤Copula可以构建系数的时变过程，对每一个交易日计算对应时变藤Copula参数，可近似地得到参数关于时间的平滑函数，然后根据式（6）、（7）得相应尾部相依系数的时变过程，由此分析不同经济时期市场恐慌情绪的传染信息。

具体做法为：与构建常系数Copula的方法类似，首先以常系数藤Copula所选择的各Copula函数为基础，根据上文给出的方法，以该常系数作为求解极大化局部似然函数的初值参数得到每个交易日相关参数，然后为其估计时变系数作关于时间的平滑函数，计算结果如图3所示。

从图3可以看到：（1）各对变量Copula函数参数均具有明显的时变效应，大体上以常参数值为中心上下波动且存在明显的波峰波谷；（2）在相当多的时期里，时变参数均大于常数估计，这表明采用常参数的藤Copula所刻画的多元变量间相依结构在大多数时候会低估变量间相依程度，造成错误的认识；（3）在个别时期如金融危机时，相关系数会急剧上升，表明恐慌情绪进入了很强的传染期；而后系数陡然下降，可以看做市场逐步走出悲观氛围，重建市场信心。

首先分析次贷危机前期及期间的市场相依结构。由图4-图6可以看到上/下尾相依系数经历了几段明显上升和下降的过程。从2004年至2005年底，香港与美国间上尾相关系数长期稳定在大约07的水平，表明两个市场恐慌情绪高度相关，一个市场对未来的悲观预期明显影响另一个市场。而2006年到2007年，上尾相依系数呈现下降态势。相应的，美国方面，2004年至2006年6月的两年时间内，美国联邦储备委员会连续17次提息，联邦基金利率从1%提到525%，2005年以来房地产市场持续降温与连续加息叠加在一起点燃了恐慌的导火线；香港方面，2003 年初爆发SARS疫情，给正在复苏的香港经济雪上加霜，当年GDP下降至1234万亿，创下自回归以来的最低值，市场被悲观氛围笼罩，一直到2005年初，香港经济才开始复苏，获得金融危机以来最高经济增长率（86%），而后经济增长虽有所放缓，但市场正逐步恢复信心。由此解释了图4中上尾相依指数由平稳到下降的演化。

类似地，对比图5大概相同的时期内，香港与韩国的上尾相依系数整体处于较低水平，表明这段时间内同处于亚洲市场的香港与韩国的恐慌情绪相互蔓延的可能性不大。结合经济发展历史可知，此时香港正处于复苏阶段，韩国经济也从上一次金融危机后得到极大回升，市场处于百废待兴的昂扬状态。对比图6中相同时间内，在已知香港恐慌预期的条件下，美国与韩国的下尾相关系数大多时间处于较低水平，同时也存在一个波峰，说明当香港市场信心走低时，美韩市场乐观情绪相关不大，但在香港逐步复苏情况下，韩国经济乐观走好的信息仍能一定程度上带给美国信心。

进入2007年后，次贷危机的影响在全球蔓延，香港与美国间的上尾相关系数从一个较小值迅速上升直到2009年末，反映此段时间由美国次货危机引爆的恐慌迅速蔓延至香港市场。此后围绕总体常系数水平上下波动。比较图4与图5可以发现，香港与韩国间的上尾相依系數也迅速上升，且长期高于总体常参数水平，至2014年才开始有所回落，说明在后次货危机时期，同处亚洲市场的香港与韩国的相关联程度相比危机前明显增大，恐慌情绪传染的可能性升高。

在危机的过程中，欧美股市大跌，新世纪金融公司、美国住房抵押贷款投资公司申请破产，金属原油期货黄金现价也大幅跳水，世界各地央行纷纷干预救市。美国政府发布了两轮金融救缓计划，首先是美联储实施了量化宽松的非常规货币政策以及一系列经济刺激计划。这些一揽子计划虽然起了积极的作用，但没有根本上解决房屋抵押品赎回权丧失问题，美股持续下跌，失业率上升。为安抚紧张的美国公众及支持经济增长，2008年10月2日美国参议院通过8 500亿美元救市方案。危机期间，香港经济整体下滑，企业出现倒闭潮，2009年首季度GDP跌至-78%，破产申请人数同比上升22%，股市成重灾区，金融业大幅裁员，楼市、旅游业疲弱。由此，香港美国的上尾相依系数一路上升，达到图4中2009年底顶点。与此同时，韩国2008年末GDP也创7年来最低，KOSPI指数比年初下降约40%，股票市场市值损失31%。香港美国、香港韩国的上尾相依程度较之前大幅提高，同时韩国美国条件下尾相依系数也显明上升，反映了次贷危机对整个亚洲市场的影响十分巨大，而且在危机中不管是恐慌情绪还是乐观情绪都大概率影响另一地区，进一步说明了危机中各市场草木皆兵的状态。

最后分析近期三个市场的相依结构。2015年以来中国经济增长放缓，股市动荡，6月来千股涨停跌停频频出现，国家队频繁出手救市防止系统性金融风险；现货金价低迷，欧美日股市也同样大幅下跌；美联储加息消息此消彼长，也给全球市场带来压力。观察以上各图所标的圆圈及箭头，图4香港与美国上尾相依系数中最右侧的拐点与2007年时非常相似，都在04附近达到最低点后出现向上的拐点；图5中近期的香港与韩国的上尾相依系数一直下降到了与2006年、2007年相似的水平；再观察图6中的条件下尾相依系数，已经出现与次贷危机时期一样迅速上升的趋势。综合三幅图不难发现，2015年以来的各时变系数与上次次贷危机前期非常相似，表明近期世界各市场投资者对未来的预期与信心与次贷危机前结构十分类似，有可能发生像次贷危机这样的全球性风险，值得相关机构部门注意。因此，时变Copula系数一定程度上可以起到风险预警作用。

（三）压力测试

一般地，当VIX指数小于20时，投资者对后市抱以乐观态度，不愿意对冲风险；当VIX大于30时，表明投资者对后市看跌恐慌情绪高涨，避险需求强烈（文辉，2010）。鉴于此，可以在给定不同市场情绪的情形下进行压力测试，以便更深入地观察各市场间恐慌情绪的联动结构。

由表3可以发现，近期在给定香港对未来预期的条件下，美国与韩国市场的反应并不相同。当香港市场投资者对未来市场越来越悲观时，韩国市场比美国市场保持乐观的可能性更大，且两个市场都保持乐观的可能性越来越小。由表4可知，当香港对后市看跌恐慌情绪高涨时，两个联合变动倾向于变得悲观，反映了恐慌情绪的传染性；且两个市场对香港市场的反映并不对称，美国市场更容易受香港市场的影响，美国恐慌情绪上升的概率变化幅度更大。

四、结论

本文借鉴Hafner and Reznikova（2010）的半参数方法，对传统的藤Copula方法进一步改进， 构建了时变参数的藤Copula模型，并利用支持向量机组成了SVM- Dynamic vine Copula的半参数系统。这种方法由数据驱动，不涉及分布与模型假设，可以很大程度地反映数据时变、偏斜尖峰厚尾等特征。利用该方法对美、韩、香港反映市场恐慌情绪的VIX指数进行建模分析，结果发现：香港与美国、香港与韩国间恐慌指数存在上尾相依，美韩间则存在条件下尾依；香港、美国、韩国投资者恐慌情绪存在传染特征，且它们之间的相依结构存在明显的时变特征，不同经濟时期对应尾部相依系数很好地符合了当时的市场环境；亚洲市场恐慌情绪的联动在次贷危机后明显加强；在金融危机中不管是恐慌情绪还是乐观情绪都大概率影响另一地区，说明危机中各市场投资者处于近乎草木皆兵的状态；2015年各市场间的相依结构与2007年、2008年次贷危机前期非常相似，表明近期各市场投资者对未来的预期与信心与次贷危机前十分类似，这值得各机构部门注意；近期两个市场对香港市场的反映并不对称，美国市场更容易受香港市场的影响，美国恐慌情绪上升的概率变化幅度更大，投资美股的投资者应该留意香港方面的情况。

参考文献：

[1]Bedford T， Cooke R M. Vines： A new graphical model for dependent random variables[J].Annals of Statistics， 2002： 1031-1068.

[2]Aas K， Czado C， Frigessi A， et al. Pair-copula constructions of multiple dependence[J].Insurance： Mathematics and economics， 2009， 44（2）：182-198.

[3]Maya L， Albeiro R， Gomez‐Gonzalez J E， et al. Latin American exchange rate dependencies： A regular vine copula approach[J].Contemporary Economic Policy， 2015，33（3）： 535-549.

[4]Heinen A， Valdesogo A. Asymmetric CAPM dependence for large dimensions： The canonical vine autoregressive copula model[J].Available at SSRN 1297506， 2008.

[5]Brechmann E C， Czado C. Risk management with high-dimensional vine copulas： An analysis of the Euro Stoxx 50[J].Statistics & Risk Modeling， 2013，30（4）： 307-342.

[6]范国斌，曾勇，黄文光.一种多资产组合风险度量解决之道：正则藤Copula[J].数量经济技术经济研究，2013（1）：88-102.

[7]杜子平， 汪寅生， 张丽.股票资产组合VaR研究：基于混合D藤Copula 模型[J].技术经济与管理研究， 2013（12）： 82-86.

[8]Patton A J. Modelling asymmetric exchange rate dependence[J].International economic review， 2006，47（2）：527-556.

[9]Hafner C M， Reznikova O. Efficient estimation of a semiparametric dynamic copula model[J].Computational Statistics & Data Analysis， 2010， 54（11）： 2609-2627.

[10]Joe H. Multivariate models and multivariate dependence concepts[M].CRC Press， 1997.

[11]文辉. 莫恐惧VIX指数[N].期货日报，2010-03-30（004）.

Abstract：Market sentiment is an important factor affecting the market trends. In order to evaluate the linkage among the panic sentiment of multi markets， the paper proposes semiparametric dynamic vine copula to describe the linkage， and uses support vector machine to estimate the density function， then it gets SVM- Dynamic Vine Copula system which doesn′t depend on assumptions of distributions and models； based on the VIX indexes of US， Korea and HK， the result shows that the dependencies of the 3 markets is time varying， and the current dependencies of them are similar to early subprime crisis which should be attended； stress test analysis gives the results that the reaction of markets is asymmetric and US market is more sensitive to HK market.

Key words：VIX index； time varying vine copula； semiparametric； support vector machine； panic sentiment

（责任编辑：张曦）