一种改进两点法无超调PID自整定算法研究
2016-05-30邹阳阳汪思源唐昌明
邹阳阳 汪思源 唐昌明
摘要:利用PID自整定算法对时滞系统进行控制是工业控制领域最常见的问题。针对阶跃响应法在工业现场不易实施, 常规Z-N控制算法整定参数不理想的问题,提出一种改进两点法无超调PID自整定算法。即在被控对象从冷态上升至设定值的过程中建立数学模型,获取被控对象的模型参数,并根据经典的PID参数整定方法即Z-N经验法提出一种对PID参数公式进行修正的方法,最后得出一组新的PID无超调整定公式。该方法具有超调量小,整定速度快,抗干扰能力强和容易在工业现场实施的特点。
关键词:时滞系统;参数自整定;Z-N整定公式;无超调;飞升曲线法
一、引言
工业领域中控制系统响应的超调量是很重要的。如何选择控制方案和最佳的控制参数一直困扰着工程技术人员。工业领域常用的整定方法方法是阶跃输出响应。但传统阶跃响应法需要对被控对象进行阶跃输出求出稳态值,对于大多数对象而言很难求出准确稳态值,在时滞系统中往往会造成控制混乱。本文提出一种基于飞升曲线避免过冲的改进两点法无超调PID参数自整定,即在被控对象从冷态上升至设定值的过程中建立数学模型,不需求取准确稳态值。以Z-N经验公式为基础构造了一个无超调PID参数整定公式,获取被控对象的模型参数,从而在线计算出PID的控制参数,达到稳定上升不超调的目的。解决了传统PID参数不易整定,超调量不易控制的难题,提高了控制精度,通过实验验证了方法可行性。
二、无过冲PID参数整定技术
(一)常规Z-N控制算法
整定经验公式基于如下带延迟的一阶惯性模型提出的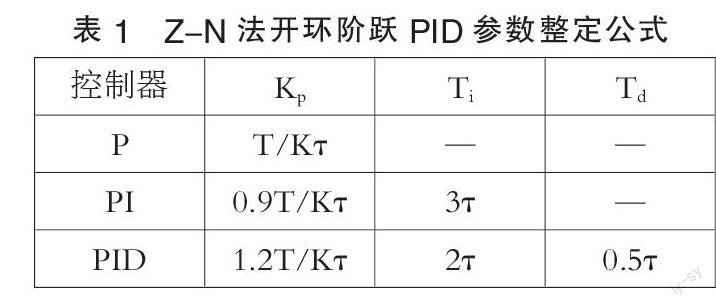
其中K, τ,T,分别为对象模型的开环增益、纯滞后时间常数和惯性时间常数。通过实验测取过程开环阶跃响应曲线,有两种求模型的方法—切线法和两点法.实际应用中,由于切线法很难准确地确定最大切线斜率点,故采用两点法。
(二)阶跃响应两点法
(三)改进两点建模
通过式(3),可以得知输出值与惯性常数T存在一定的对应关系,找到系统在阶跃给定下的稳态值就可以求出系统传递函数,在实际环境下不可能对被控对象进行阶跃给定求取传函,即使给定,也不能获取理想稳态值。况且环境不同,稳态值也会不同,从而系统模型也不尽相同。即便同一个被控对象,其稳态值不固定也不唯一。甚至可以广义认为大于0.865y(∞)的任一值为稳态值。下面给出改进两点法参数自整定控制器模型,如图1所示。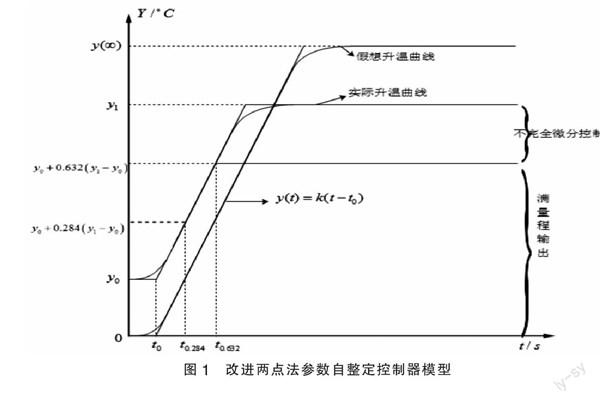
实验两点选取t0.284和t0.632分别是达到y0+0.284(y1-y0)和y0+0.632(y1-y0)温度的时间,t0是滞后时间。
再根据式(5)得到PID三个参数。
对1000ml水箱,采用改进两点法从常温至45度加热。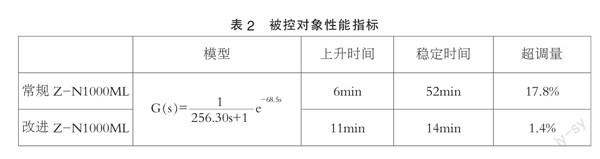
应用常规Z-N法不能够实现对水箱无超调控制,且控制量输入受外界噪声影响过大。这是因为水箱的τ值过大,常规Z-N法根据4:1衰减比整定出微分过大,对噪声干扰加大,而且该系统τ/T<0.6 常规Z-N法很难实现无超调。这都将造成超调。故根据大量实验,对Z-N公式进行修正。
比例部分:作用增大。因为比例的大小影响系统响应的超调量.
积分部分:作用减小。减少系统超调量。
微分作用:作用减小。考虑到PID控制器的微分作用具有超前的预测作用,并且影响系统的快速性与稳定性。未修正的微分系数过大,一定量的减弱后,能够达到更好的快速性和稳定性。
三、实验验证及结果分析
同样对1000ml容量水箱,应用(6)无超调整定公式进行从常温至45度加热。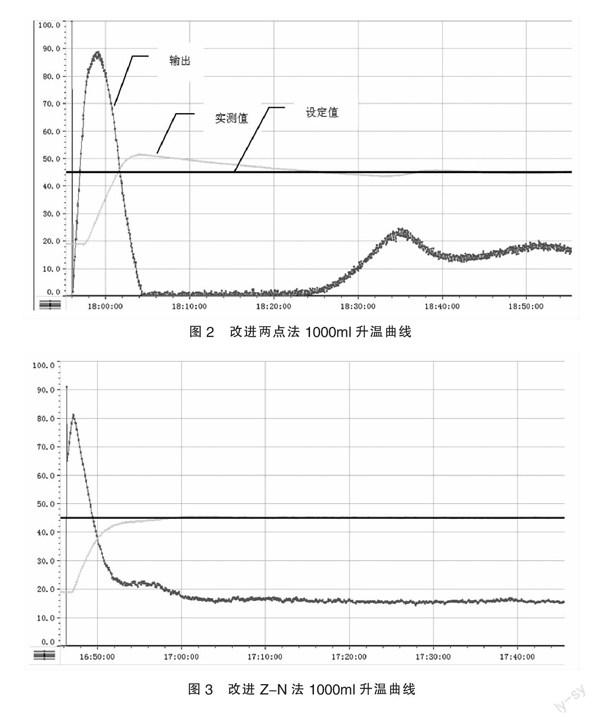
从上述升温曲线以及表2中,可以看出改进后的两点法无超调自整定算法控制效果比较好,明显减少了控制过程的超调量,实现了高精度控制。
四、总结
改进两点法无超调自整定算法实现了不需要对系统进行阶跃输出求取稳态值就可以较为精准得到系统的模型。并根据经典的PID参数整定方法即Z-N经验法提出了一种对PID参数公式修正的方法,最后得出一组新的PID无超调整定公式。文中对相同容量的被控对象做了对比实验,从而验证了此方法具有较好的控制效果。可推出这种参数自整定方法具有很大的工业应用价值。
参考文献:
[1]李国林. PID控制器参数整定技术研究与优化设计[D].大连理工大学,2010.
[2]何芝强. PID控制器参数整定方法及其应用研究[D].浙江大学,2005.
[3]刘玉贞.无超调PID控制器的设计[D].杭州电子科技大学,2011.
[4]杨帆.具有PID自整定功能的温度控制器研究与实现[D].大连理工大学,2006.
[5]韩帮华.PID控制器参数整定方法及应用研究[D].青岛科技大学,2009.
*本文受大连市科技计划项目(2014E11SF059)、中央高校基本科研业务费专项资金资助。
(作者单位:大连海事大学)
