基于可拓理论的RBF网络模型在多属性决策中的应用研究
2016-05-30何楠韩瑞魏含笑
何楠 韩瑞 魏含笑
摘要:多属性决策一直是管理科学领域中的一个难题,现有的理论针对这个问题给出了很多方案优选的方法和模型,但均有各自的优势与不足。多属性决策的难点在于难以明晰多属性决策中各个属性的量化指标与决策方案的优劣的非线性关联,而神经网络的拟合能力与泛化能力决定了其在多属性决策中广阔的应用前景。将可拓理论的相关思想作为基础,创造性地对多属性决策矩阵进行处理从而构建出径向基函数(Radial Basis Function,RBF)网络模型的学习样本,结合RBF网络模型优秀的拟合能力和泛化能力,最终通过训练后的RBF网络模型得到较优的决策方案。
关键词:可拓理论;RBF网络模型;多属性决策
一、引言
多属性决策问题往往表现为方案选优问题,即在有限个评价指标下对各个方案的优劣进行排序的问题。但是,在面对这种问题的时候,我们往往并不知道每个评价指标的权重应当如何确定。根据决策者是否带有主观倾向,可以将赋权法分为主观赋权法和客观赋权法,典型的主观赋权法有专家调查法、层次分析法、二项系数法等;典型的客观赋权法则有熵权法、AHP等。主观赋权法易使决策方案带有较大的主观性影响,而客观赋权法则往往无法体现决策者的合理倾向,无论是主观赋权法还是客观赋权法,均难以克服其自身的局限性。
对于RBF网络模型而言,其自身的结构、算法主要决定了模型处理问题的能力和性能,而学习的样本,则最终决定了RBF网络模型拟合能力和泛化能力的具体体现。现有理论已经证明,具有单隐层的前馈网络可以影射所有的连续函数,只有当学习不连续函数时,才需要两个隐层。对于有限的多属性方案优选问题,在不知道具体的方案评价规则时,神经网络作为最有效的函数逼近工具,其非线性、自学习、自适应等特点使得其在解决此类问题方面中具有其他方法无法比拟的优势。但是,RBF网络模型并没有在决策领域充分发挥其应用潜力,原因之一就是难以获得足够数量的学习样本。
本研究基于可拓理论中关于将方案的优劣评级转换为方案在决策属性下的不同等级值域的思想,创造性地构造出RBF网络模型的学习样本,使得RBF网络模型具备了对方案的优选能力,并最终通过RBF网络模型的评价得出了方案的优劣顺序。这种方法避开了广受争议的赋权过程,形成了既能反映出决策者合理倾向又能在相当程度上避免较大主观影响的方案优选方法。
二、基于可拓理论的RBF网络模型构建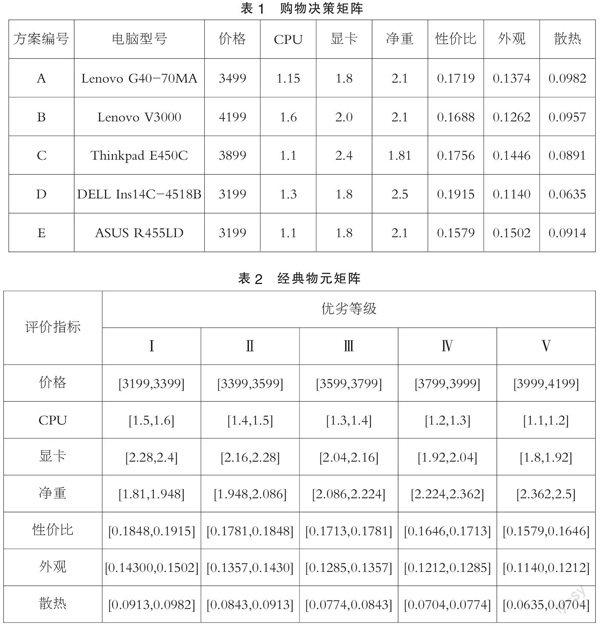
面对多属性决策问题,将决策方案直接与方案的优劣等级相关联是比较困难的。可拓理论通过建立经典物元矩阵,以可拓距离描述决策方案的现实属性与经典物元之间的远近关系,并计算关联函数值,最终结合各决策属性的权重计算每个方案与不同决策评级值域的综合关联度。综合关联度的大小体现了决策方案与各个方案优劣等级之间的相符程度,值越大说明决策方案越应当被评价为该优劣等级。
本研究正是基于这样的问题解决策略,提出了如下神经网络的学习样本构建方法。
(一)确定决策矩阵
其中,Rk为第k个方案优劣等级的经典物元矩阵(k=1,2,…,l);Sk为所划分的第k个优劣等级;Ij为第j个评价指标(j=1,2,…,n);Xjk为第j个指标在第k个优劣等级的量值范围;ajk、bjk为第k个优劣等级下第j个指标值域的下限值和上限值。
(三)确定神经网络学习样本
根据经典物元矩阵构建神经网络学习样本的输入矩阵P以及期望输出矩阵Q。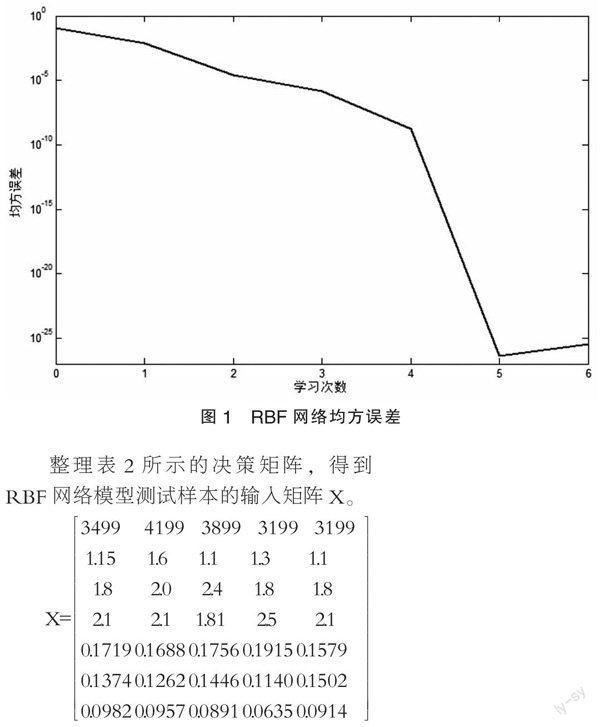
输出矩阵Q是指当决策方案的各项属性指标达到最优等级的上限值时,RBF网络模型输出为1,表示当前为最优决策方案;当各项属性指标达到最劣等级的下限值是,RBF网络模型的输出为0,表示当前为最差决策方案;而当各项属性指标为其他等级的相应上下限值时,RBF网络模型的输出则按照等级的相应顺序以线性内插法确定。
通过以上三个步骤,最终建立起RBF网络模型的学习样本,从而使训练后的RBF网络模型具备了评价现有决策方案优劣的泛化能力。
三、实证分析
目前,计算机已经相当普及,随着社会节奏的加快,网络购物业已成为了人们尤其是工薪阶层的首选消费方式。但是,网络购物在带给人们便利的购物体验的同时,也在无形中增加了人们的决策难度。网络购物使得人们在购物的时候能够跨越空间的距离,无视本地商品库存状况,增加了人们购物选择的多样性。与此同时,这也使得人们更加容易陷入难以抉择的困境——我到底应该买哪一个商品?
人们在通过网络选择商品时,只能通过网页图片、商品参数等信息来判断商品的优劣。网络商品的用户评价在相当程度上也能给予人们一定的决策指导,但是这些通过网络所获得的信息在某种意义上来说是一种间接获取的信息,这种信息获取形式往往让除了卖家以外的人难以确定哪些信息是真实的而更应当被重视,从而使人们在这种典型的多属性决策中,从观念上的主观偏好变为了事实上的无主观偏好。在这种情况下,网络购物的决策者们发现,他们比以往任何时候都更加难以确定各个决策属性的权重。既然权重问题成为了网络购物多属性决策困境的主要原因,是否有一种可行的方法让决策者们避开权重呢?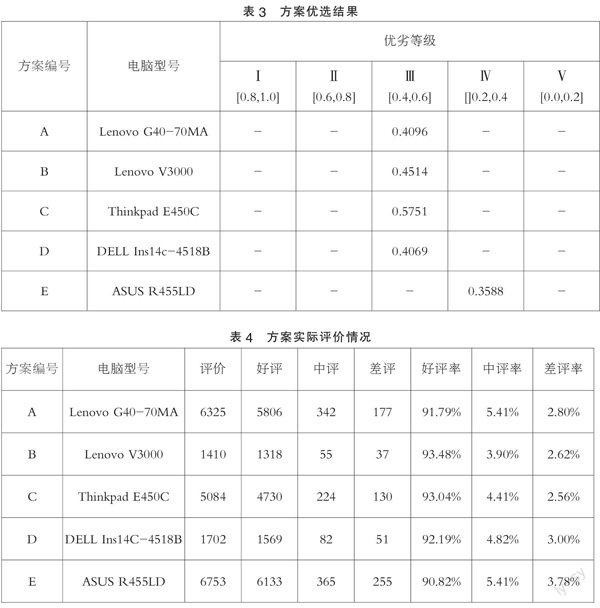
本研究以2015年6月10日某购物网站上的五种不同型号的热销笔记本电脑作为研究样本,并将一切可以从网页中提取的量化指标作为决策属性,具体包括价格、CPU性能指数、显卡性能指数、净重、性价比指数、外观指数和散热指数作为决策指标,以基于可拓理论的RBF网络模型进行多属性决策,从而得出方案优选的结果,并将优选结果与各电脑型号的实际评价状况进行比较,最终证明该方法的合理性、有效性和便捷性。
将统计数据以式(1)的形式进行整理得到决策矩阵如表1所示。其中,CPU性能指数与显卡性能指数通过专业跑分软件对电脑硬件进行测试得到;净重则为实际的重量,单位为千克;性价比指数、外观指数、散热指数则由商品买家评论中相对应的指标评论数比上累计评论数得到。
以每个评价属性的最劣值作为该属性节域的下限值,最优值则作为该属性节域的上限值。并建立从优到劣I、II、III、IV、V五个级别,故对节域进行五等分从而得到5个经典物元矩阵。根据表1和式(2),将5个经典物元矩阵进行整合,得到如表2所示的经典物元矩阵。
在Matlab 2012b环境下,调用newrb函数生成一个结构为7-6-1的RBF网络模型,即输入层神经元数目为7,隐含层神经元数目为6,输出层神经元数目为1的三层前馈神经网络模型。根据多次试凑,将RBF的扩展速度设置为5,以使RBF网络模型在拟合性与网络性能之间取得平衡。将输入矩阵P进行归一化处理后对RBF网络模型进行训练,训练到第5次时达到最小网络均方误差s=3.59804×10-26。绘制RBF网络模型的均方误差曲线如图1所示。
整理表2所示的决策矩阵,得到RBF网络模型测试样本的输入矩阵X。
将输入矩阵进行归一化处理后通过学习完毕的RBF网络模型中进行评价,得到输出矩阵Y。
整理输出矩阵Y,得到如表3所示的方案优选结果。
由于优劣等级是以所有方案的属性最优值和最劣值作为该属性节域的上限值和下限值并等分为五级而确定的,且所有方案均为该购物网站上的热销机型,因此各个方案必然密集在一个中等的等级即等级III上。事实上,也正是因为每个方案均为热销机型,才给购物者带来了相当的决策难度,这也说明了得到如表3所示的结果是符合实际情况的。而在所有的决策方案中,C方案的综合指数最高,说明其为最优的购买选择;而E方案的综合指数最低,在对各个评价属性没有明显偏好的情况下,其各项指标的综合影响难以在该评价体系下形成优势,为最劣的购买选择。将各个方案以综合指数从大到小的顺序排列可得:C>B>A>D>E。
整理2015年6月10日某购物网站中各个电脑的实际评价情况并制成表4,将满意的购物解读为不会给予差评的购物,则购物方案应以差评率由小到大的顺序进行排序,即:C>B>A>D>E,与模型评价结果相符。因此,本方法是一个行之有效的多属性决策方法。
四、结语
赋权方法的选择一直在多属性决策中备受争议,而基于可拓理论的RBF网络模型凭借其自身特性可以跳过赋权过程,直接使输入数据与相应评级建立映射关系,该方法逻辑清晰明了、操作简单可行,既能在建立经典物元矩阵和评价等级的过程中反映出决策者合理倾向,又能在相当程度上避免较大主观影响。由基于可拓理论的RBF网络模型得出的结果与实际的评价情况相符,说明该方法有效、可行,能够为其他类似的多属性决策问题提供案例与参考。
参考文献:
[1]梵治平,赵萱.多属性决策中权重确定的主客观赋权法[J].决策与决策支持系统,1997(04).
[2]施彦,韩力群,廉小亲.神经网络设计方法与实例分析[M].北京邮电大学出版社,2009.
[3]Wang J, Malakooti B. A feedforward neural network for multiple criteria decision making[J].Computer Operations Research,1992(02).
[4]蔡文,杨春燕.可拓学的基础理论与方法体系[J].科学通报,2013(13).
[5]胡兴俊,严小丽.建筑施工方案安全性的熵权可拓综合评价[J].上海工程技术大学学报,2014(02).
[6]马永红,王晓彤.基于熵权物元可拓的区域创新系统成熟度评价[J].统计与决策,2014(22).
(作者单位:华北水利水电大学管理与经济学院)
