加权值多态蚁群算法

鲍文杰　朱信忠　赵建民　徐慧英

摘 要：本文提出加权值多态蚁群算法。在信息素初始化时加入权值，加大各条路径之间的信息素差异，利于蚂蚁快速进行路径选择；在概率选择过程中加入权值，提高蚂蚁搜索效率；采用了蚁周模型对信息素进行全局更新，并且设置了信息素最大值，避免算法陷入局部最优解。最后采用均匀分布的方法确定参数值，通过仿真实验结果表明，该方法在TSP问题中具有良好的稳定性和高效性。

关键词：蚁群算法；权值；均匀分布；信息素

中图分类号：TP301.6 文献标识码：A

Abstract：This paper proposes weighted value polymorphic ant colony algorithm.Added weight when pheromone initialization，increased pheromones differences between the paths，beneficial to the ants select path quickly.Added weight when select probability，improve ants search efficiency.Adopted Ant-Cycle System，updated the pheromones and set up the max pheromones ，avoid the algorithm fall into local optima.Adopted evenly distribution method to determine parameter，simulation results show that the algorithm possesses good stability and efficiency.

Keywords：ants colony algorithm；weight；evenly distributed；pheromone

1 引言（Introduction）

旅行商问题（Traveling Salesman Problem，TSP），是一个经典的路径问题，它可以描述为：在n个城市的范围内，一个推销员要遍历范围内所有城市推销自己的商品。该推销员从一个城市出发，需要经过所有给定的城市后，最后回到出发地的最小路径成本，故也常被称作“推销员问题”。从图论的角度看，也就是找出一个最短封闭路线的问题[1]。TSP问题是数学领域中一个非常经典的问题之一。

蚁群算法根据蚂蚁的群体行为特性，模仿自然界中的蚂蚁寻找食物到蚁巢之间最短路径的行为，寻找搜索问题的最优解。在自然界中真实蚂蚁在寻找食物过程中，能够在其走过的路径上释放一种分泌物，称之为“信息素”，蚂蚁可以根据路径上的信息素浓度来决定前进的方向[2]。早在1911年，意大利学者Dorigo M受到启发，在他的博士论文中提出了蚁群算法。

2 蚁群算法的数学模型（Ants colony algorithm）

设m表示蚁群中蚂蚁的总数量；n表示城市个数；表示城市i的坐标；表示城市i和城市j之间的距离；表示t时刻路径（i，j）上的信息素浓度；表示t时刻城市i和城市j之间的启发程度，通常取；为信息素启发因子；为期望启发因子；为信息素挥发因子，表示在时间内衰减的系数；表示t时刻路径上的信息素增量；表示在t时刻，蚂蚁k从城市i转移到城市j的概率；表示蚂蚁k禁忌表；将m只蚂蚁放置在n个城市上，每个蚂蚁通过感知该城市周围路径上的信息素浓度，按照下式选择下一步即将访问的城市。

显然，蚂蚁转移概率与信息素浓度成正比，而与路径长度成反比，也就是说，信息素浓度越大，路径越短，蚂蚁选择这条路径的概率就越大。当蚂蚁遍历了地图上所有城市后，完成一次循环，记为蚂蚁k走过的路径长度，并保存最短路径。此时清空禁忌表中的所有元素，并把当前所在城市添加到禁忌表中，准备进入下一次遍历。路径上的剩余信息素会随着时间的流逝慢慢挥发，各条路径上的信息量按照以下规则更新[3]。

其中，表示信息素残留系数。Dorigo M给出了三种不同的基本蚁群算法模型，用以针对各类不同的信息素更新机制，分别是蚁周模型、蚁量模型和蚁密模型。

3 加权值多态蚁群算法（Weighted value polymorphic ant colony algorithm）

在加权值多态算法设计中，由于工蚁并不参与到路径寻优的工作中，故在加权值多态蚁群算法中，我们将蚁群分为侦查蚁和搜索蚁，取消了工蚁。其中，m1表示侦查蚁个数；m2表示搜索蚁个数；n表示城市个数；表示信息素权值；表示概率权值；表示最大信息素值；在初始时刻，为了加大各条路径之间的初始信息素浓度的差异，在信息素初始化时加入权值，使得距离当前蚂蚁所在城市较近的城市的初始信息素浓度明显大于较远城市，如此一来，蚂蚁一开始就会选择较短路径，并且有利于后续蚂蚁的快速寻优。具体公式如下：

当蚂蚁到达一个城市时，就要进行状态转移概率选择。如果蚂蚁附近的MAXPC个城市尚未被访问过，路径上的侦查素，则在概率选择过程中加入权值，使得蚂蚁以较大概率选择这些城市。若蚂蚁附近的MAXPC个城市全部已经被访问过，路径上的侦查素，蚂蚁将会根据普通概率公式选择其余尚未被搜索过的城市，如下公式：

为了防止在某些路径上的信息素浓度过高，使得所有蚂蚁都选择该路径，避免算法陷入局部最优，提高蚂蚁寻优效率，算法中还借鉴了Thomas等人提出的最大最小蚁群算法（Max-Min Ant System），在算法中加入了信息素浓度最大值，在每次循环中各条路径上的信息素更新完毕后，对各条路径上的信息素浓度进行判断，若信息素浓度大于，则将信息素浓度强制设为。在同一个问题规模中，的值根据循环次数做出调整，一般来说，会随着循环次数的增加而变大。

加权值多态蚁群算法步骤如下：

步骤1：初始化各个参数值，侦查蚁个数m1，搜索蚁个数m2，城市个数n，常数Q和C，信息素启发因子，期望启发因子，加入权值和，最大循环数值，MAXPC，最大信息素值。

步骤2：把m1只侦查蚁放置于n个城市中，每只侦查蚁侦查其他个城市，释放侦查素。

步骤3：初始化各路径上的信息素浓度。

步骤4：初始化循环次数NC=0。

步骤5：把m2只搜索蚁随机放置在n个城市中，每只搜索蚁将当前所在城市添加到禁忌表tabu。

步骤6：根据概率转移公式，搜索蚁k选择下一步即将访问的城市，并且将该城市添加到tabuk，当m2只搜索蚁全部访问遍所有城市，记为一次迭代。

步骤7：记录本次循环中的最短路径。

步骤8：更新各条路径上的信息素浓度。

步骤9：判断各路径上的信息素浓度是否大于，若是，则将其强制设定为。

步骤10：置，清空禁忌表tabuk，。转至步骤五。

步骤11：输出最优解。

4 仿真实验（Simulation）

在蚁群算法求解各类路径寻优问题中，参数设置是十分重要的一个环节，若各项参数设置不合理，则算法容易陷入局部最优解，不能很好地求得最优解。那么有没有简单的方法，能够快速方便的从这些实验组合中找到最优组合呢？于是，我们很自然的想到了均匀设计法。根据ATT48TSP，对加权值多态蚁群算法进行实验。需要确定的参数的取值范围为：蚂蚁数目；信息素挥发因子；

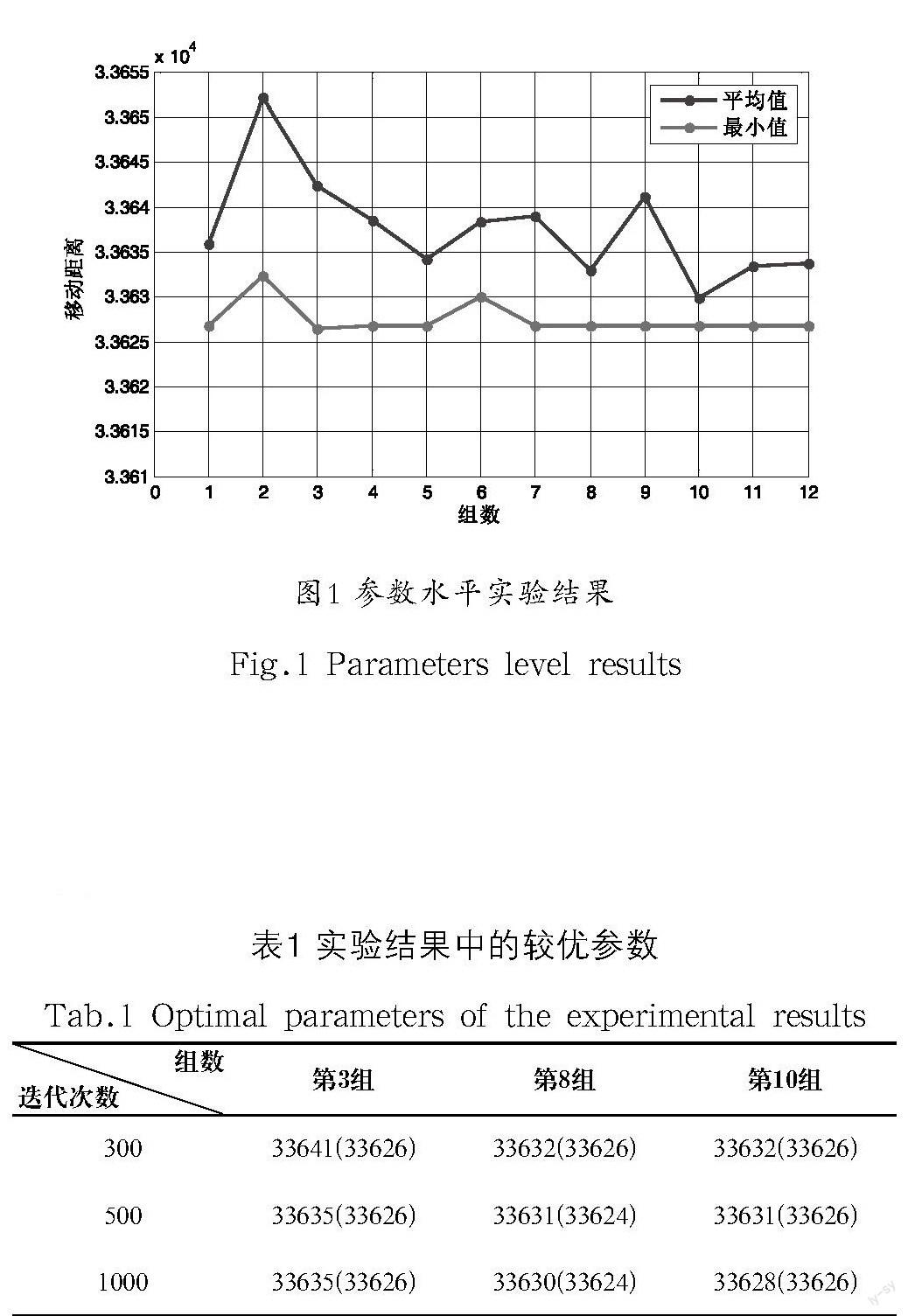
信息素启发因子；期望启发式因子；权值；权值；参数个数s=6，选择均匀设计表。对每组参数进行300次迭代的实验，最后实验结果的最小值并且计算出平均值，如图1所示。

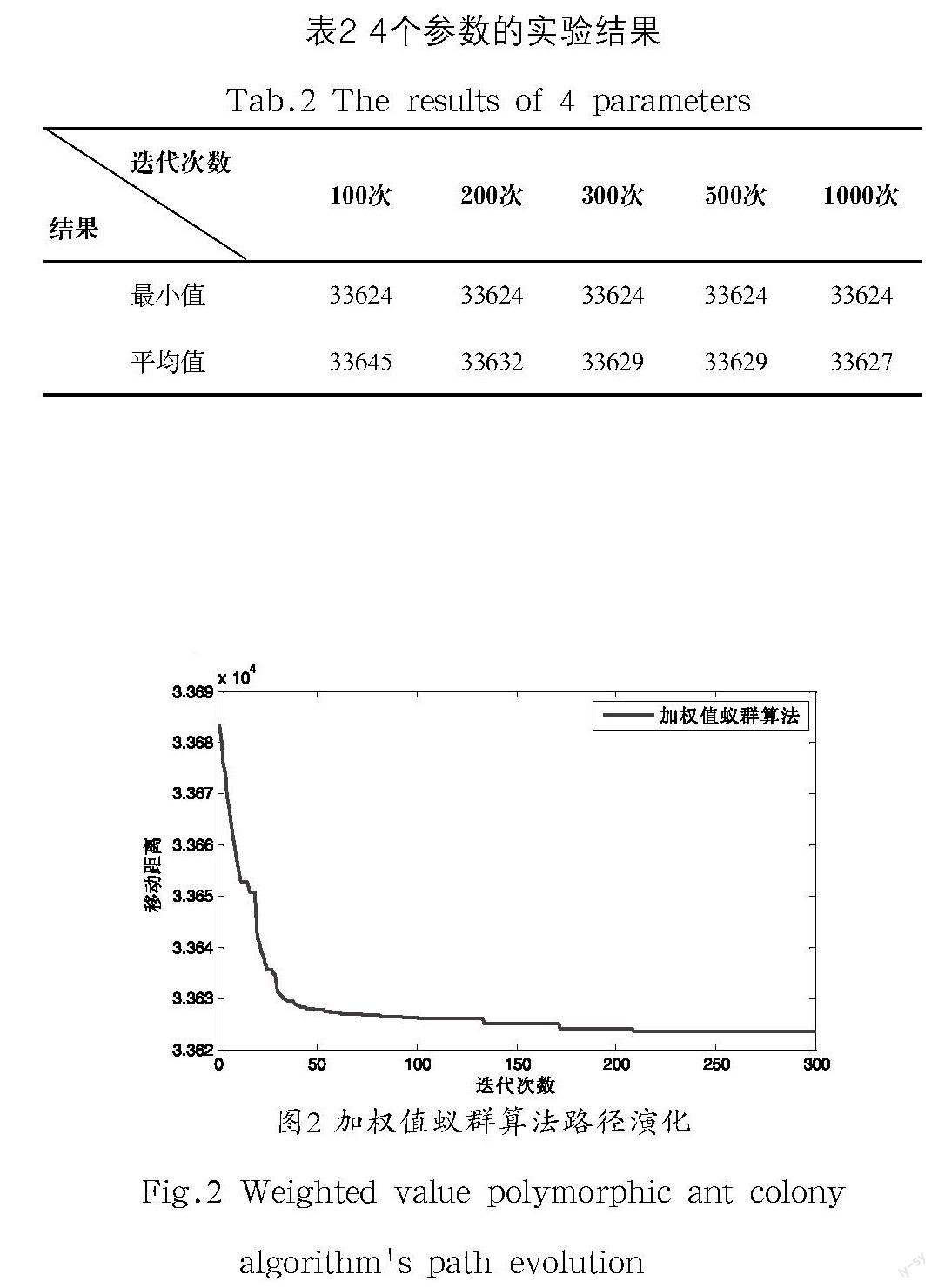
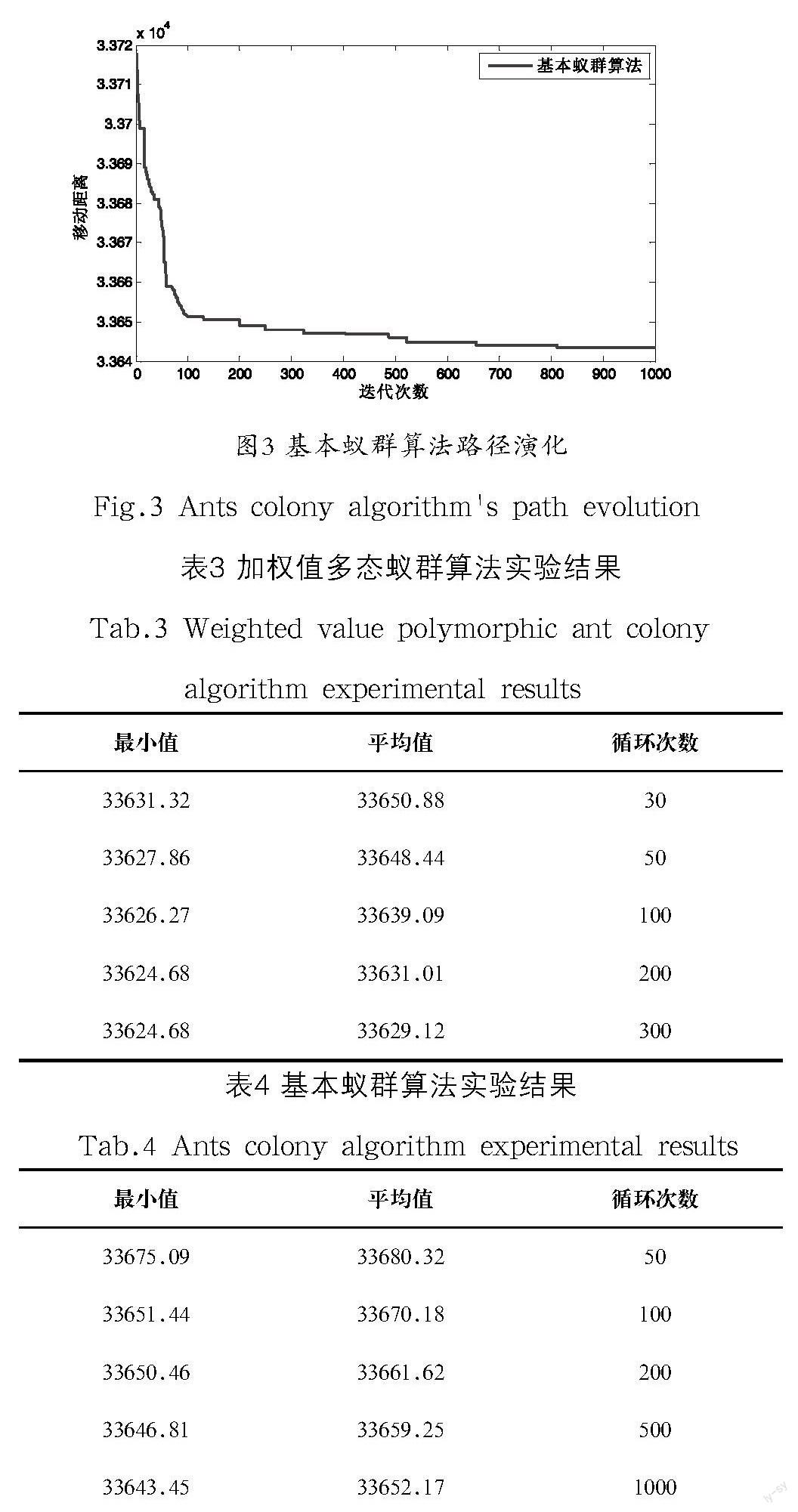
可见，加权值多态蚁群算法不仅可以求得更好的解，还具有更好的高效性。加权值多态蚁群算法是比基本蚁群算法更好更合理的求解TSP问题的方法。这得益于两个权值和，有了和的加入，蚂蚁在进行路径选择时，会优先选择距离较近的城市，大大提高侦查素在寻优过程中起到的作用，并且在加快收敛速度的同时，有效的避免了搜索陷入局部最优解。即使没有侦查素的存在，蚂蚁也可以选择其他城市，很好的解决了在多态蚁群算法中，蚂蚁在同一个城市重复搜索而某些城市不被搜索的问题，并且通过公式，蚂蚁可以在更短的时间内寻找到最短路径，极大地提高了搜索效率，缩小了搜索范围。

5 结论（Conclusion）

本文通过在算法中加入权值的方法，对多态蚁群算法进行了优化设计，使蚂蚁能够更快的进行路径选择，提高蚂蚁搜索效率。对信息素更新机制做了改进，避免算法陷入局部最优解。

本文提出的加权值多态蚁群算法不仅可以解决TSP问题，还可以解决一系列无规则的路径规划问题，也可扩展到其他领域应用。在此基础上，将该算法与基本蚁群算法进行比较，进一步说明其优越性。

参考文献（References）

[1] 宋志飞.基于蚁群算法的TSP问题研究[D].江西理工大学，2012.

[2] 岳凤.多态蚁群算法及其应用[D].山东师范大学，2009.

[3] 陈建玲.基于蚁群算法的优化问题研究[D].大庆石油学院，2007.