A Description of Fixed Subgroups of Free Groups∗

Qiang ZHANG

1 Introduction

Throughout this paper,let F be a finitely generated free group.

The rank of F,denoted by r(F),is the cardinality of a basis of F.As usual,Aut(F)denotes the automorphisms of F,End(F)denotes the endomorphisms of F,and Inj(F)denotes the injective endomorphisms of F.

Let φ :F → F be an endomorphism of F.We will denote φ as acting right of argument,and x → (x)φ (the parentheses will be omitted if there is no risk of confusion).A subgroup H ≤ F is called φ-invariant if Hφ ≤ H.In this case,the restriction of φ to H will be denoted by φ|H:H → H,which is an endomorphism of H.

Except when r(F)=1,Inn(F),the subgroup of inner automorphisms,is isomorphic to F.For any y ∈ F,we will write γyto denote the inner automorphism of right conjugation by y(denoted by exponential notation).Thus γy:F → F,x → xγy=y−1xy=xy.Similarly,for any subgroup H ≤ F,we denote by Hy=y−1Hy its right conjugation by y.

The fixed subgroup of an endomorphism φ of F,denoted by Fixφ,is the subgroup of elements in F fixed by φ:

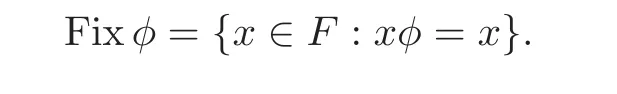
Following[8],a subgroup H≤F is called 1-auto- fixed(resp.1-endo- fixed and 1-inj- fixed),when there exists an automorphism(resp.endomorphism and injective endomorphism)φ of F such that H=Fixφ.

In[9],Stallings raised a question:What subgroups S of F can be of the form Fixβ?Here,β refers to an automorphism of the free group F.

It is easy to see that the trivial subgroup is 1-auto- fixed.Also a cyclic subgroup H= 〈x〉of F is 1-auto- fixed if and only if it is pure,i.e.,xr∈H implies x∈H,and in this case,H=Fixγx(for more details,see[7]).So,the interesting cases begin with subgroups of rank 2.

The maximal-rank case was completely settled by Collins and Turner.In[3],they gave a complete description of the 1-auto- fixed subgroups H≤F with r(H)=r(F).

The goal of this paper is to generalize Martino-Ventura’s results(Theorem 1.1 below)to injective endomorphisms(Theorem 1.2 below).In[7],Martino and Ventura generalized Collins and Turner’s results, finding a similar description which applies to all 1-auto- fixed subgroups without restriction.For later use,we give the Martino-Ventura result below.

Theorem 1.1(see[7,Theorem 1.4])Let F be a nontrivial finitely generated free group and φ ∈ Aut(F)such that Fixφ1.Then,there exist integers r,s≥ 0,φ-invariant non-trivial subgroups K1,···,Kr≤ F,primitive elements y1,···,ys∈ F,a subgroup L ≤ F,and elements 1h′j∈ Hj=K1∗ ···∗ Kr∗ 〈y1,···,yj〉,j=0,···,s − 1,such that

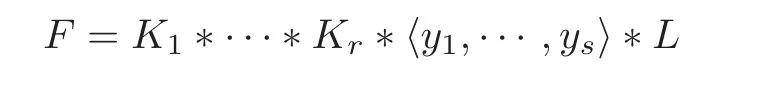
and yjfor j=1,···,s;moreover,

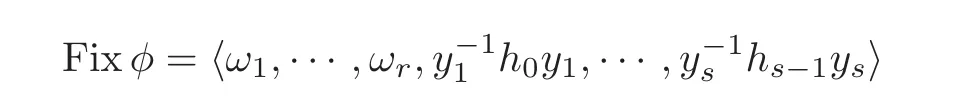
for some non-proper powers 1ωi∈ Kiand some 1hj∈ Hjsuch that1,···,r,j=0,···,s− 1.

Remark 1.1 For 1h0∈ H0=K1∗···∗Kr,we can know that H0=K1∗···∗Kr1.So,in fact,r≥1 in Theorem 1.1.

A subgroup H≤F is called a free factor of F,if it admits a basis which can be extended to a basis of F.Thus,if H is a free factor of F,then there exists a subgroup L≤F,such that F=H∗L.For any free factor H≤F,we have r(H)≤r(F)with equality if and only if H=F.

An element ω ∈ F is called an F-primitive element when there exist words ω2,ω3,···,ωnsuch that{ω,ω2,···,ωn}is a basis of F.

In this paper,we show that the Martino-Ventura result(Theorem 1.1)also holds for inj- fixed subgroups in free groups,that is the following theorem.

Theorem 1.2 Let F be a nontrivial finitely generated free group and φ∈Inj(F)such that Fixφ1.Then,there exist integers r≥ 1,s≥ 0,φ-invariant non-trivial subgroups K1,···,Kr≤ F,primitive elements y1,···,ys∈ F,a subgroup L ≤ F(L1 if φAut(F)),and elements 1∈ Hj=K1∗ ···∗ Kr∗ 〈y1,···,yj〉,j=0,···,s − 1,such that

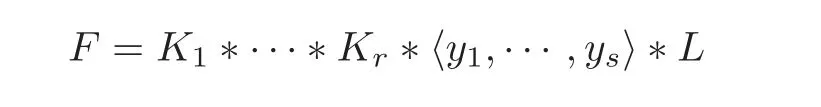
and yjfor j=1,···,s;moreover,

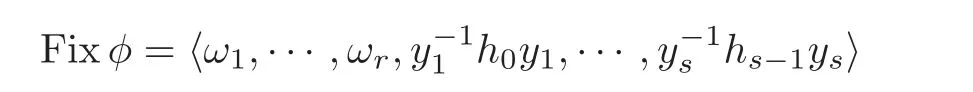
for some non-proper powers 1ωi∈ Kiand some 1hj∈ Hjsuch that1,···,r,j=0,···,s− 1.

This paper is organized as follows.In Section 2,we will give the proof of Theorem 1.2,and in Section 3,we will give some corollaries and examples.

2 Proof of Theorem 1.2

In this section,we will prove Theorem 1.2.

Definition 2.1 Suppose φ ∈ End(F).Then we denote by Fφ∞the stable image of φ,i.e.,

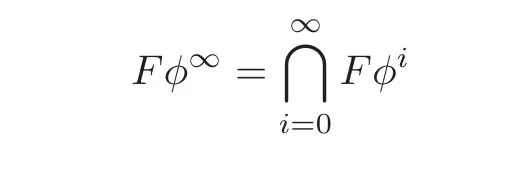
and

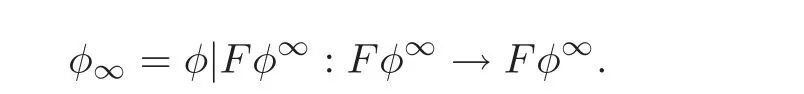
It is shown in[5]that r(Fφ∞)≤r(F),φ∞is an automorphism,and clearly Fixφ=Fixφ∞≤Fφ∞.

Lemma 2.1 Let φ∈Inj(F)be an injective endomorphism of the finitely generated free group F.Then Fφ∞is a free factor of F,i.e.,

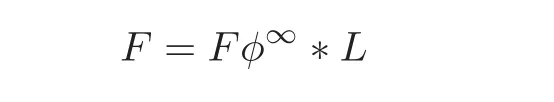
for a subgroup L≤F;moreover,L=1 if and only if φ∈Aut(F).

Proof It follows from[6,Problem 33 on p.118]that Fφ∞is a free factor of Fφnfor almost all n.So there exists an integer n and a subgroup L′≤ F such that

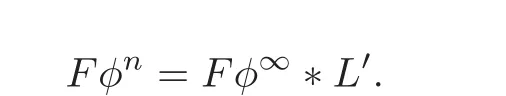
Since φ ∈ Inj(F),φn:F → Fφn=Fφ∞∗L′is an isomorphism.Let L=L′(φn)−1.Then

Clearly,L=1 if and only if φ∈Aut(F).

Proof of Theorem 1.2 If φ is surjective,then φ ∈ Aut(F),by Theorem 1.1,we have done.

Otherwise,following Lemma 2.1,we have F=Fφ∞∗L′′,L′′1,and 1 ≤ r(Fφ∞)＜ r(F),so Fφ∞is finitely generated.Applying Theorem 1.1 to Fφ∞and φ∞∈ Aut(Fφ∞),there exist integers r≥ 1,s≥ 0,φ∞-invariant non-trivial subgroups K1,···,Kr≤ Fφ∞,primitive elements y1,···,ys∈ Fφ∞,a subgroup L′≤ Fφ∞,and 1h′j∈ Hj=K1∗···∗Kr∗〈y1,···,yj〉,j=0,···,s− 1,such that ands;moreover,

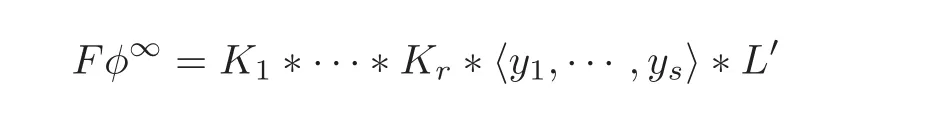
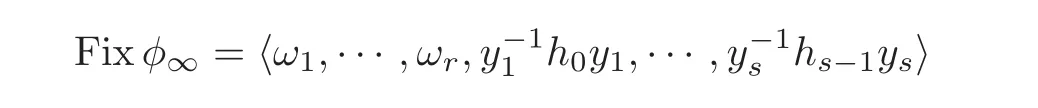
for some non-proper powers 1ωi∈ Kiand some 1hj∈ Hjsuch that1,···,r,j=0,···,s− 1.

Let L=L′∗L′′.Then L1.Since φ∞= φ|Fφ∞and Fixφ =Fixφ∞,we have

and

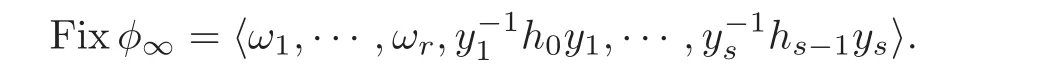
Thus Theorem 1.2 holds.

3 Some Corollaries and Examples

In this section,we will give some corollaries and examples of Theorem 1.2.

From Theorem 1.2,we immediately have the following corollary.

Corollary 3.1(see[1,10])Let Fnbe the free group of rank n and φ :Fn→ Fnbe an injective endomorphism.If φ ∈ Aut(Fn),then r(Fixφ) ≤ n;if φ /∈ Aut(Fn),then r(Fixφ) ≤n−1.

In fact,it is also shown in[10]that if φ :Fn→ Fnis an endomorphism which is not an automorphism,then r(Fixφ)≤n−1.So,we have the following definition.

Definition 3.1 A subgroup H≤Fn(n≥2)is called maximum-rank 1-endo- fixed(resp.1-inj- fixed)if there exists an endomorphism(resp.injective endomorphism)φ of F such that

Corollary 3.2 If φ∈Inj(F)with maximum-rank 1-inj- fixed subgroup,then there exist integers r ≥ 1,s ≥ 0,and primitive elements ω1,···,ωr,y1,···,ys,z ∈ F(z=1 if and only if φ∈Aut(F)),such that

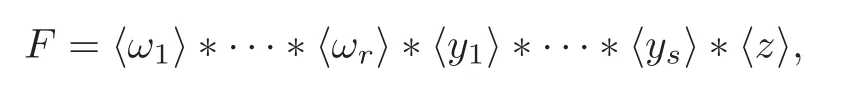
andmoreover,

for some 1hj∈ Hjsuch that

Proof Following from Theorem 1.2,we have

Since r(Ki)≥ 1,we have r(Ki)=1.Thus Ki;moreover,since Kiφ ≤ Kiand Fixφ∩Ki=〈ωi〉,we have Ki= 〈ωi〉,i=1,···,r.

Remark 3.1 When φ ∈ Aut(F)and r(Fixφ)=r(F),Corollary 3.2 is the main result of[3].

From the example below,we can easily know that Corollary 3.2 does not hold for φ∈End(F)with maximum-rank 1-endo- fixed subgroup.

Example 3.1 Let F= 〈a,b〉be a free group of rank 2 freely generated by{a,b},and let φ∈End(F)be given by

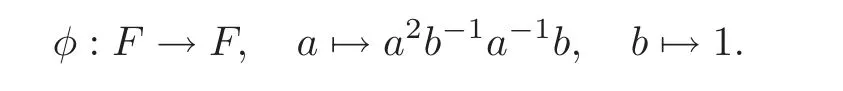
Then it is easy to know that

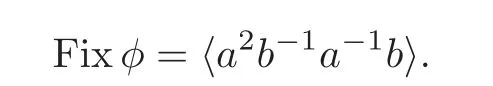
So,〈a2b−1a−1b〉is a maximum-rank 1-endo- fixed subgroup of F.However,following from[2],a2b−1a−1b is not a primitive element of F.So,Corollary 3.2 does not hold for φ ∈ End(F).

Corollary 3.3 Every injective endomorphism of Fn(n≥2)with maximum-rank 1-inj- fixed subgroup fixes a primitive element of Fn.

Proof It follows immediately from Corollary 3.2.

Remark 3.2 When φ ∈ Aut(F)and r(Fixφ)=r(F),Corollary 3.3 is the main theorem of[4]:Every automorphism of Fnwith a fixed subgroup of rank n fixes a primitive element of Fn.

If the injective endomorphism φ of Fnis not with the maximum-rank 1-inj- fixed subgroup,then Corollary 3.3 does not hold.

Example 3.2 Let F= 〈a,b〉be a free group of rank 2 freely generated by{a,b},and let φ∈Aut(F)be given by

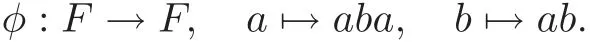
Then it is easy to know that

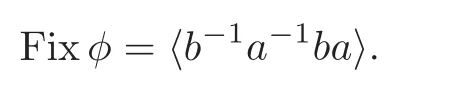
Clearly,b−1a−1ba is not a primitive element of F.So,Fixφ contains no primitive elements.

Acknowledgements The author would like to thank Prof.Boju Jiang for valuable communications and suggestions.The author also thanks the referee for his or her comments.

[1]Bestvina,M.and Handel,M.,Train tracks and automorphisms of free groups,Ann.of Math.,135,1992,1–51.

[2]Cohen,M.,Metzler,W.and Zimmermann,A.,What does a basis of F[a,b]look like?Math.Ann.,257,1981,435–445.

[3]Collins,D.and Turner,E.,All automorphisms of free groups with maximal rank fixed subgroups,Math.Proc.Cambridge Philos.Soc.,119,1996,615–630.

[4]Collins,D.and Turner,E.,An automorphism of a free group of finite rank with maximal rank fixed point subgroup fixes a primitive element,J.Pure Appl.Algebra,88,1993,43–49.

[5]Imrich,W.and Turner,E.,Endomorphisms of free groups and their fixed points,Math.Proc.Cambridge Philos.Soc.,105,1989,421–422.

[6]Magnus,W.,Karrass,A.and Solitar,D.,Combinatorial Group Theory,Wiley,New York,1966.

[7]Martino,A.and Ventura,E.,A description of auto- fixed subgroups in a free group,Topology,43,2004,1133–1164.

[8]Martino,A.and Ventura,E.,On automorphism fixed subgroups of a free group,J.Algebra,230,2000,596–607.

[9]Stallings,J.,Graphical theory of automorphisms of free groups,Combinatorial Group Theory and Topology,Ann.of Math.Stud.,Vol.111,Princeton University Press,Princeton,NJ,1987.

[10]Turner,E.,Test words for automorphisms of free groups,Bull.London Math.Soc.,28,1996,255–263.