Stochastic H2/H∞Control for Poisson Jump-Diffusion Systems∗

Meijiao WANG

1 Introduction

In many realistic situations,the noise for a dynamic system may be Wiener-or Poisson-type.Poisson noises cause the random discontinuity of the system dynamic,whereas Wiener noises cause the continuous perturbation of the system dynamic.Poisson processes should be also considered when a dynamic system is exposed to sudden,infrequent,highly localized changes that occur in a short period of time such as earthquakes,large random weather fl uctuations,or occasional mass mortalities.Poisson processes quite frequently arise in engineering,manufacturing,economics,and biosystem applications.For example,in financial market,the stock price is classically described by geometric Brownian motion,however,in practice,the price of stocks can be made a sudden shift by the exogenous disturbance such as wars,decisions of large banks or the corporation,national policy,block transaction etc.In order to describe such phenomena,Poisson jumps is usually inserted in and thus the control system is governed by independent Brownian motion and Poisson random jumps,which is called Poisson jump-diffusion systems(see[18,24]).The optimal control problem with random jumps was first considered by Boel and Varaiya[1].In their case,the control system is disturbed by random jumps and the optimal solution is a discontinuous stochastic process.From then on,many scholars began to study the jump-diffusion system and its applications,for further reference,we refer to[8,17,20]and their references.Those results mostly concentrate on optimal control and its application in financial markets or their corresponding theories.

H∞control and H2/H∞control are important robust control design methods in modern control theory.H∞control requires a controller to eliminate the external disturbance below a given disturbance attenuation level,while H2/H∞control demands one to minimize an average output energy while guaranteeing a prescribed disturbance attenuation level.Before 1998,most works are focused on deterministic H∞and H2/H∞control for the systems governed by an ordinary differential equation(see[4,13–14,19]).In recent years,quite a lot of research interests have been devoted to stochastic Itsystems.For example,in Hinrichsen and Pritchard[10],H∞control for general linear stochastic Itsystems was firstly discussed very extensively.Moreover,a very useful lemma called “stochastic bounded real lemma(SBRL for short)” was given therein using linear matrix inequalities.Then Zhang and Chen[26]investigated H∞control of nonlinear stochastic systems with multiplicative noise,where a Hamilton-Jacobi equation(HJE for short)associated with nonlinear stochastic H∞control was derived.As for the H2/H∞control,Chen and Zhang[2]studied the mixed H2/H∞control with state-dependent noise,and then a further discussion on the case of nonlinear stochastic Itsystems with state,control input and external disturbance-dependent noise((x,u,v)-dependent noise for short)was given in[27],both of which extended the deterministic H2/H∞control results of[14]to the stochastic setting.More recently,Wang[23]discussed the H2/H∞control with state-dependent noise and random coefficients,where the sufficient and necessary conditions for the existence of the H2/H∞control are given by a pair of coupled backward stochastic Riccati equations.This result extended the work of Chen and Zhang[2]to the case of random coefficients.

In addition,stochastic H∞and H2/H∞control for discrete or continuous time Itsystems with Markovian jumping parameters also have attracted many researchers’attention.For instance,in a recent monograph(see[7]),H∞control has been elaborately addressed for discrete-time Markov jump systems with multiplicative noise.The state and output feedback H∞control of nonlinear stochastic Markov jump systems with state and disturbance dependent noise has been tackled in[15]based on coupled Hamilton-Jacobi inequalities.Hou et al.[11]studied the in finite horizon H2/H∞control problem for a broad class of discrete-time Markov jump systems with(x,u,v)-dependent noise.For other relevant developments in this regard,interested readers can refer to the monographs as Dragan and Morozan[5–6],Todorov and Fragoso[21–22],etc.

As mentioned above,most works on stochastic H∞and H2/H∞control are constrict in Itstochastic systems or Markovian jump systems,but Poisson noise was not considered in these papers.While in engineering practice,the dynamic systems,such as electric power systems,aircraft flight control systems and manufacturing systems,may experience dramatic changes when suffering sudden external impact as power failure,atmospheric turbulence in extreme weather and machine breakage or repair.In this situation,it is very nature to utilize the Poisson jump-diffusion process to describe such phenomena(see[3,16]).Lin[16]studied the H∞control problem for a class of Poisson jump-diffusion stochastic linear systems with constant coefficients.Chen[3]investigated the H∞robust control designs for nonlinear stochastic systems with external disturbance and Poisson noise,where a fuzzy approach to solve the Hamilton-Jacobi inequality(HJI for short)was employed.However,to the best of our knowledge,there are rare literature concerning stochastic H2/H∞control for jump-diffusion systems.The objective of this paper is to develop an H2/H∞control theory for Poisson jump-diffusion systems with(x,u,v)-dependent noise and time-varying coefficients,and sufficient and necessary conditions are derived for the existence of a state feedback H2/H∞control in terms of four coupled matrixvalued Riccati equations.To some extent,the results of this paper can be viewed as an extension of that of[2]to the case of(x,u,v)-dependent noise and random jumps.

The rest of this paper is organized as follows.In Section 2,we present two useful lemmas and describe some basic theories on stochastic H∞and H2/H∞control.In Section 3,inspired by the ideas in[10],we develop the stochastic bounded real lemma for Poisson jump-diffusion system,which enables us to obtain necessary and sufficient conditions for the existence of a stabilizing controller which keeps the effect of the perturbation on the to-be-controlled output below a given disturbance attenuation level.Based on this result,we then derive necessary and sufficient conditions for the existence of stochastic H2/H∞control in Section 4.Concluding remarks are presented in Section 5.

2 Problem Formulation and Preliminaries

2.1 Notations

We make use of the following notations in this paper.

M′is the transpose of the vector or matrix M. |M|denotes the square root of the summarized squares of all the components of the vector or matrix M. 〈M1,M2〉is the inner product of two vectors M1and M2.M−1is the inverse of a nonsingular square matrix M.Rmstands for the m-dimensional Euclidean space.C(τ,T;H)is the space of H-valued continuous functions on[τ,T]endowed with the maximum norm.(τ,T;H)is the space of H-valued Ft-adapted cdlg processes f on[τ,T]satisfying(τ,T;H)is the space of H-valued Ft-adapted square-integrable stochastic processes f on[τ,T]satisfying ‖f‖ =Lν,2(E;H)is the space of H-valued measurable functions f defined on the measurable space(E,B(E),ν)satisfying([0,T]× E;H)is the space of Lν,2(E;H)-valued and Ft-predictable processes f satisfy-is the space of Rk-valued and Ft-predictable processes f on[τ,T]satisfying

Sometimes we may write f for a deterministic function ft,omitting the variable t,whenever no confusion arises.Under this convention,when f ≥ (＞)0 means ft≥ (＞)0 for all t∈ [0,T].

2.2 Two useful lemmas

Throughout this paper,let T be a fixed strictly positive real number and(Ω,F,{Ft}0≤t≤T,P)be a complete filtered probability space on which is defined one-dimensional standard Brownian motion{Wt}0≤t≤T.Denote by B(Ξ)the Borel-σ-algebra of any topological space Ξ.Let(E,B(E),ν)be a measurable space with ν(E) ＜ ∞ and η :Ω × Dη→ E be an Ft-adapted stationary Poisson point process with characteristic measure ν,where Dηis a countable subset of(0,∞).Then the counting measure induced by η is

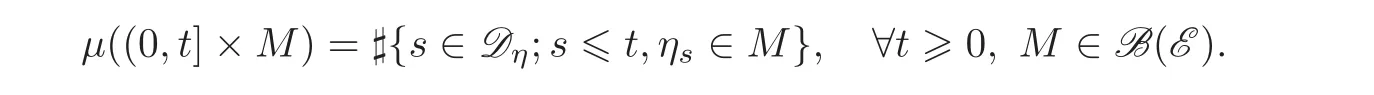
And(dθ,dt):=μ(dθ,dt)− ν(dθ)dt is a compensated Poisson random martingale measure which is assumed to be independent of Brownian motion.Assume that{Ft}0≤t≤Tis P-completed natural fi ltration generated by{Wt,0≤t≤T}and???A×(0,t](dθ,dr),0≤t≤

Now we state some basic results on stochastic differential equation(SDE for short)driven by both martingale and Poisson jumps which will be frequently used in this paper.One is the It’s formula of this type process(see[9]),the other is the solution’s existence and uniqueness of stochastic differential equation driven by Brownian motion and Poisson random jumps(see[12]).

Lemma 2.1 Let Mtbe a square integral continuous martingale and Atbe a continuous adapted process with finite variance.g=(g1,···,gn),here gi(s,x,θ),i=1,···,n is{Ft}t≥0locally square integrable,and x0is an F0-measurable variable.xtsatisfies the following Ittype stochastic process:

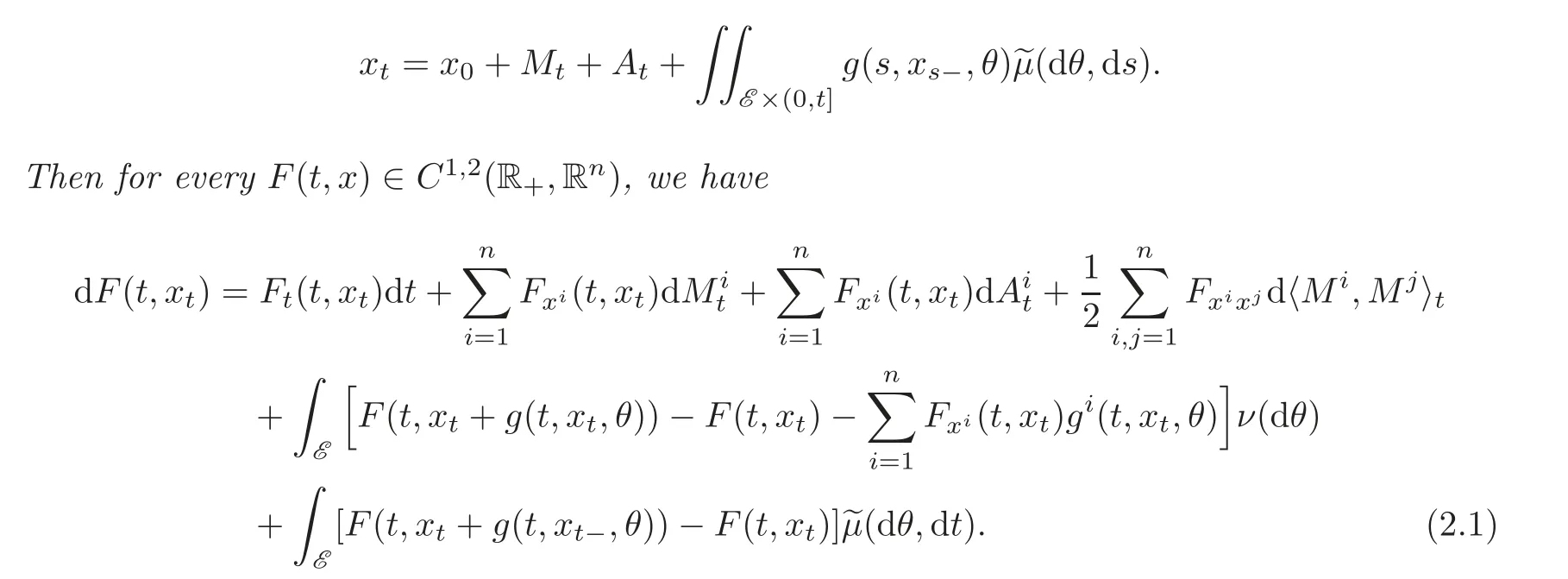
Here,〈·,·〉denotes the quadratic variation process of the semi-martingale,and F(t,x)∈C1,2(R+,Rn)denotes function F(t,x)being twice continuously differentiable in x ∈ Rnand once in t∈R+.Fxand Fxxdenote the gradient row vector and Hessian matrix with elements of second partial derivatives of n-dimensional function F(t,x),respectively.

Lemma 2.2 Let x0be an F0-measurable random variable and b:[0,T]×Ω×Rn→Rn,σ:[0,T]×Ω×Rn→Rn,π:[0,T]×Ω×E×Rn→Rnare given mappings satisfying

(i)b(·,0)∈ L2F(0,T;Rn);σ(·,0)∈ L2F(0,T;Rn);π(·,·,0)∈ Lν,2F([0,T]× E;Rn);

(ii)for some positive constant C ＞0,and for all(t,x,x)∈[0,T]×Rn×Rn,there exists

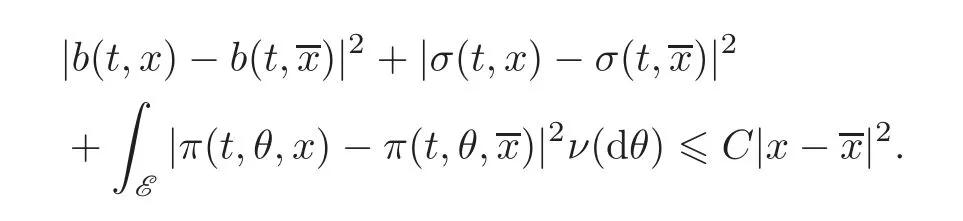
Then the stochastic differential equation with jumps

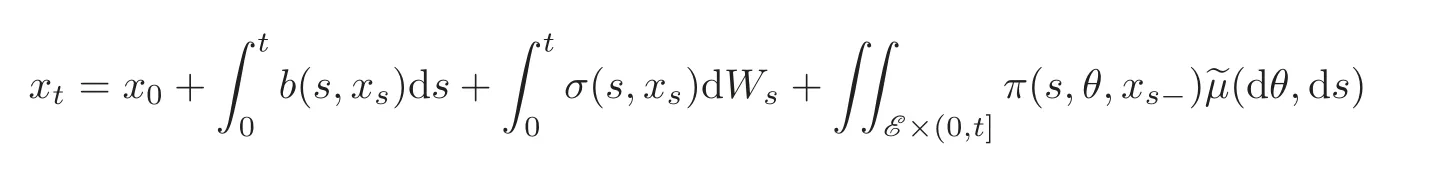
has a unique solution x∈S2F(0,T;Rn).Moreover,a priori estimate holds:

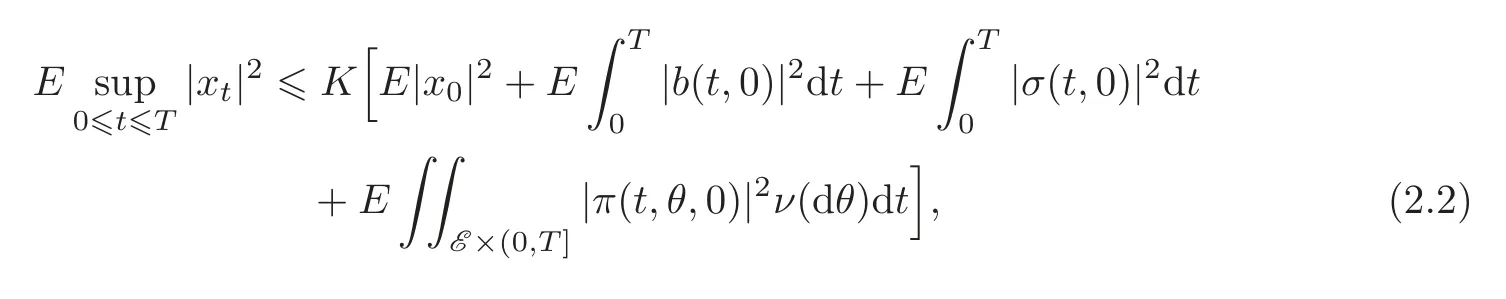
where K is a positive constant depending only on Lipschitz constant C and T.

2.3 Problem formulation

Consider the following stochastic time-varying linear system governed by Brownian motion Wtand Poisson random martingale measure?μ(dθ,dt):

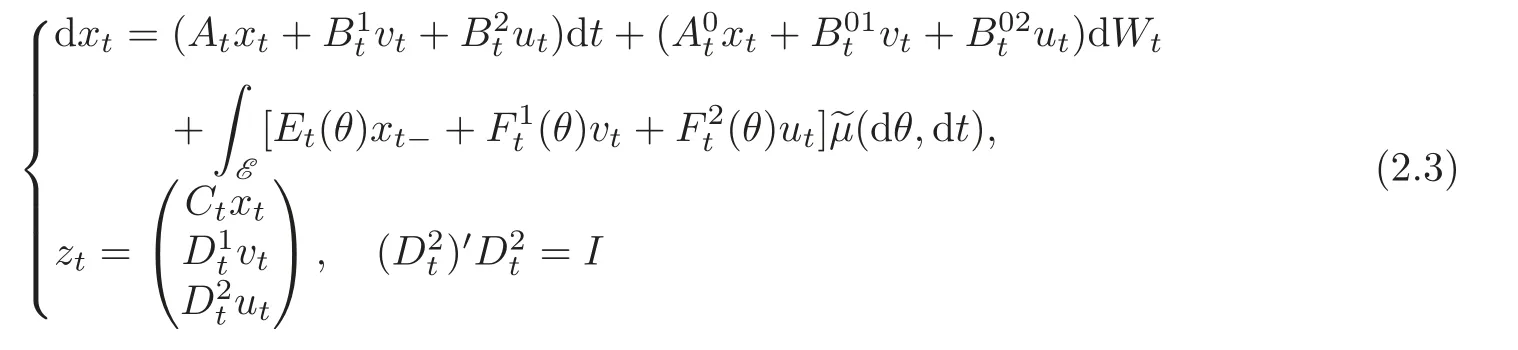
with x0=x0.We assume the coefficient matrices A,A0:[0,T]→ Rn×n,B1,B01:[0,T]→Rn×m,B2,B02:[0,T]→ Rn×s,C:[0,T]→ Rq×n,D1:[0,T]→ Rl×m,D2:[0,T]→ Rp×s,E:[0,T]→ Lν,2(E;Rn×n),F1:[0,T]→ Lν,2(E;Rn×m),F2:[0,T]→ Lν,2(E;Rn×s)are matrixvalued continuous functions.Then from Lemma 2.2 for all(u,v,x0)∈ Us[0,T]×Um[0,T]×Rn,there exists a unique solution x=x(·,u,v,x0) ∈(0,T;Rn)to the state equation of system(2.3).

We view v as an external disturbance which adversely affects the to-be-controlled output z ∈ Rq+l+p(whose desired value is represented by 0).The disturbing effect is to be ameliorated via control input u ∈ Us[0,T].The effect of the disturbance on the to-be-controlled output z of the system(2.3)is then described by the perturbation operator Lcl:Um[0,T]→Uq+l+p[0,T]being defined as Lcl(v)=(Ctx(·,u,v,0),vt,ut)′,which(for zero initial state)maps finite energy disturbance signals v into the corresponding finite energy output signals z of the closed loop system.The size of this linear operator is measured by the induced norm.The larger this norm is,the larger is the effect of the unknown disturbance v on the to-be-controlled output z in the worst case.Then the H∞control problem is to determine whether or not for each γ ＞ 0 there exists a stabilizing controller u∗achieving ‖Lu∗‖ ＜ γ,where Lu∗:[′,T]→ U+↕+[′,T]can be defined as Lu∗ (v)=(Ctx(·,,v,0),vt,)′.Obviously,there may be more than one solution satisfying the required condition.We want the control not only to guarantee robust stability,but also to minimize the output energy when the worst case disturbance is implemented to the system,this is the so-called H2/H∞control problem.That is,we wish to:

(1)Find a feedback control u∗∈ Us[0,T]such that the norm of the perturbation operator of the system(2.3)is less than some given disturbance attenuation level γ ＞ 0,i.e.,‖Lu∗‖ ＜ γ;

(2)We require the control u∗to minimize the output energy z when the worst case disturbance v∗∈ Um[0,T]is applied to the system(2.3).

As we will show,this problem may be formulated as an LQ nonzero sum game.The two cost functionals we use are defined as follows:

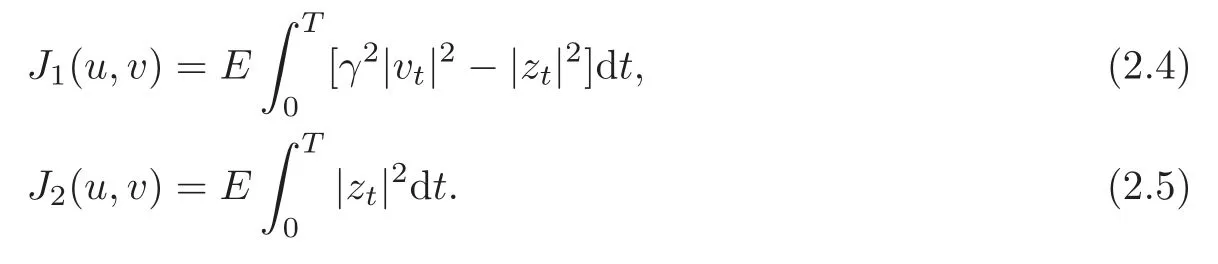
The first one is associated with an H∞robustness,while the second one reflects an H2optimality requirement.The aim is to find equilibrium strategies u∗and v∗defined by

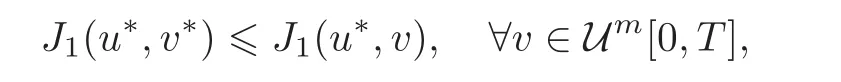
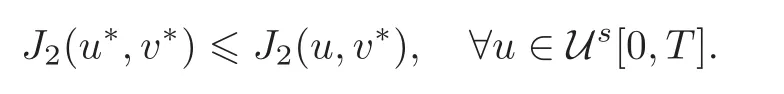
If J1(u∗,v∗)≥ 0 with x0=0,certainly ‖z‖2≤ γ2‖v‖2for all v ∈ Um[0,T],which ensures that‖Lu∗‖ ≤ γ.The second Nash inequality shows that u∗minimizes output energy z when the external disturbance is at its worst and given by v∗.For example,in flight control system,the worst case disturbance means the extreme whether as atmospheric turbulence,while the corresponding control input means the control effort which minimizes the energy loss and sensitivity to the worst case atmospheric disturbances.Clearly,if the Nash equilibria(u∗,v∗)exist,then u∗is our desired H2/H∞controller,and v∗is the corresponding worst case disturbance.Then the H2/H∞control problem can be converted into finding the Nash equilibria(u∗,v∗).We approach this problem as linear quadratic(LQ for short)optimal control problem and obtain the solution by studying the associated stochastic Riccati equation.

In the following,we will give sufficient and necessary conditions for the existence of linear state feedback pairs(u∗,v∗).To this end,we will make some preliminaries in the next section.

3 Stochastic Bounded Real Lemma for Jump-Diffusion Systems

In this section we shall develop a version of stochastic bounded real lemma(SBRL for short),which states necessary and sufficient conditions for a given stochastic system with jumps to be stable with ‖L‖ ＜ γ.It is of independent interest,because it allows one to determine ‖L‖which measures the influence of the disturbances in the worst case scenario.To this end,we consider the following linear stochastic system:

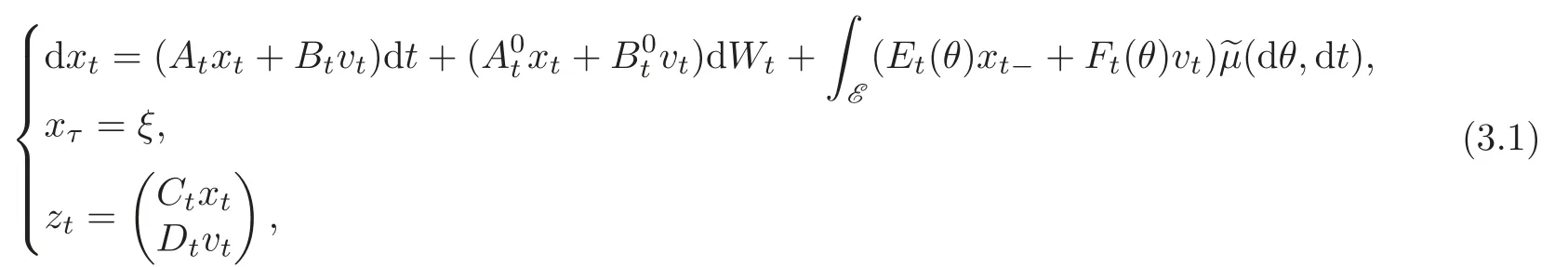
where(τ,ξ) ∈ [0,T]× Rnare the initial time and initial state,respectively. We denote v ∈ Um[τ,T]as the external disturbance and z ∈ Uq+l[0,T]the controlled output.All the coefficients A,A0:[0,T]→ Rn×n,B,B0:[0,T]→ Rn×m,C:[0,T]→ Rq×n,D:[0,T]→ Rl×m,E:[0,T]→ Lν,2(E;Rn×n),F:[0,T]→ Lν,2(E;Rn×m)are matrix-valued continuous functions.For all(v,ξ) ∈ Um[τ,T]× Rn,there exists a unique solution x=x(·,v;τ,ξ) ∈(τ,T;Rn)to the state equation of system(3.1).We use z defined in(3.1)rather than the more natural zt=Ctxt+Dtvtonly to avoid the appearance of cross terms when computingNote that we assume the Brownian motion to be one-dimensional just for simplicity,there is no essential difficulty in the analysis below for the multidimensional cases.

Definition 3.1 The system(3.1)with initial state zero is said to be externally stable or L2input-output stable if there exists a constant γ≥0 such that

Definition 3.2 Suppose that the system(3.1)is externally stable.The operator L:Um[0,T]→Uq+l[0,T]defined by

is called the perturbation operator of(3.1).Its norm is defined as the minimal γ≥0 such that(3.2)is finished,i.e.,

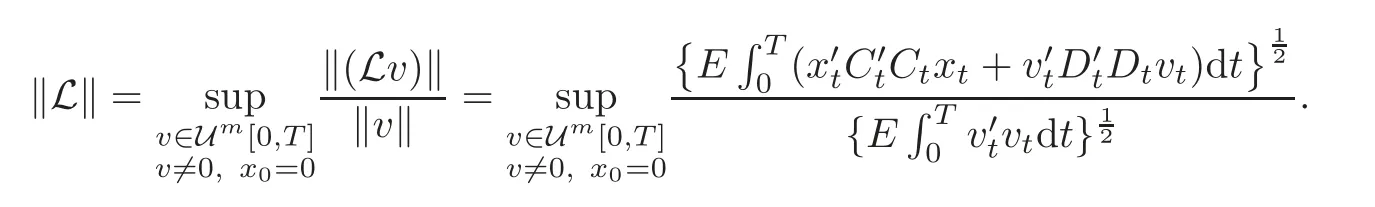
‖L‖ is a measure of the worst effect that the stochastic disturbance v may have on the to-becontrolled output z of the system.Therefore it is important to find a way of determining the norm ‖L‖.The stochastic bounded real lemma which we will derive in this section provides a method for computing ‖L‖.

We proceed by associating a finite time quadratic cost functional with the problem parameterized by the initial data(τ,ξ) ∈ [0,T]× Rn,v ∈ Um[τ,T]and z ∈ Uq+l[τ,T]:

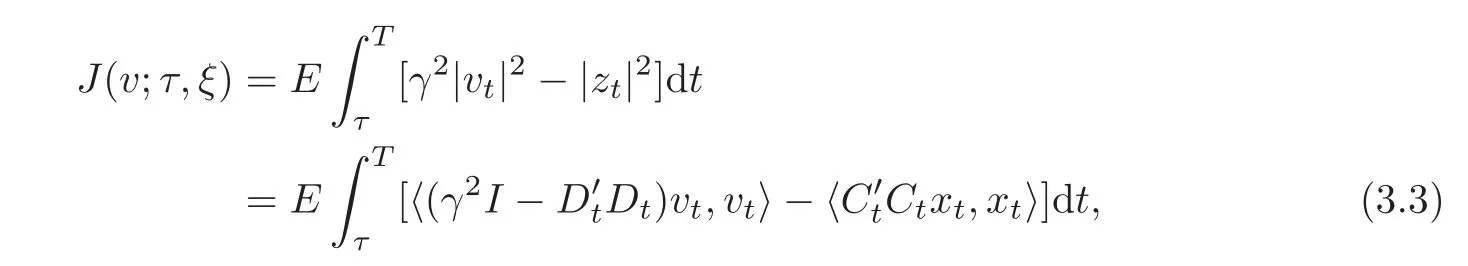
where x denotes the solution of(3.1).Note that for a given γ＞0,the cost functional J(v;0,0)is nonnegative for all v∈ Um[0,T]if and only if‖L‖ ≤ γ.Therefore,the problem of minimizing this functional will lead us a method for estimating ‖L‖.We will analyze the linear quadratic(LQ for short)stochastic optimal control problem:Minimize the functional J(v;τ,ξ)over v ∈ U [τ,T]subject to(3.1).In our development in this section,we will employ the usual convention in LQ theory and refer to the disturbance v as a “control”.

The above LQ problem is indefinite as the control weighting matrix in the cost is positive definite,while the state weighting matrix is negative semi-definite,which leads to the following indefinite stochastic Riccati equation(SRE for short):

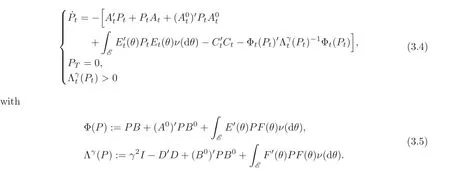
The global solvability of SRE(3.4)is hard to prove due to the following reasons:First,it is a highly nonlinear ordinary differential equation(ODE for short),especially in view of the matrix inverse term(Λγ(P))−1,the existence and uniqueness theorem of solution of linear ODE is not valid.Second,the indefiniteness of coefficient matrices makes possible the singularity of the term Λγ(P)when one tries to use the typical approximation scheme to construct a solution.

Third,the final positive definiteness constraint in(3.4)is the part of the equation and must be finished by any solution.Finally,(3.4)is a matrix equation,thus certain terms do not commute which adds substantial difficulty to the analysis.Hence,a new way to obtain its solution should be found.

In the following,we will prove the so-called stochastic bounded real lemma,which plays an essential role in this paper.

Theorem 3.1(Stochastic Bounded Real Lemma)Given γ ＞ 0,‖L‖ ＜ γ if and only if the stochastic Riccati equation(3.4)parameterized by γ has a unique negative semi-definite solution P≤0.

The next proposition proves the above theorem in one direction,i.e.,establishes a relation between‖L‖ ＜ γ and the existence of some P ≤ 0 such that the stochastic Riccati equation(3.4)is solvable.

Proposition 3.1 Suppose that SRE(3.4)is solvable for some pair(γ,P)with γ ＞ 0 and P being negative definite and uniformly bounded,then LQ problem is solvable with the optimal control vt= Ψtxt−,t∈ (0,T]and ‖L‖ ＜ γ,where Ψt= −(Pt)−1Φ(Pt).

Proof Suppose that SRE(3.4)has a solution,and let x be the solution of(3.1)with xτ= ξ.Applying It’s formula(2.1)to 〈Ptxt,xt〉,together with considering(3.3)and using the completion of squares,we have

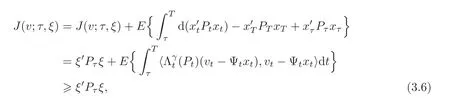
whereIt follows immediately that the optimal feedback control would be vt= Ψtxt−if the corresponding solution to the system equation exists.In this case,the optimal cost isIn fact,when vt= Ψtxt−,the system(3.1)reduces to

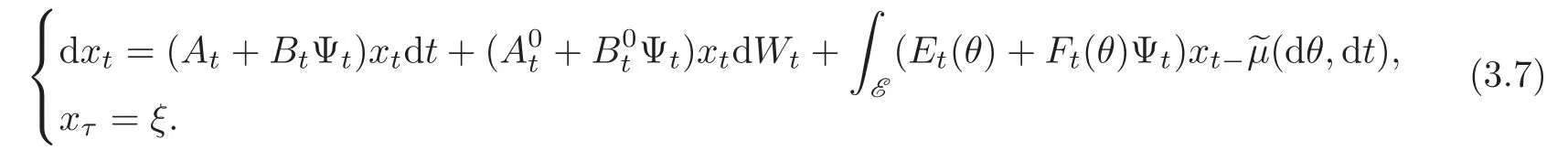
In view of the third positive definiteness constraint in(3.4),there exists a sufficient small∈＞ 0 such that(Pt) ≥ ∈I for all t ∈ [τ,T].Moreover,since P is negative definite and uniformly bounded,all the coefficients of(3.7)are continuous and uniformly bounded.Therefore linear SDE(3.7)indeed has a unique solution x ∈(τ,T;Rn),thus,v= Ψx ∈ Um[τ,T].Here and in the following,v= Ψx denotes{vt= Ψtxt−}t∈(τ,T],where Ψ ∈ C(τ,T;Rm×n).

From(3.6),we derive that J(v;0,x0)≥ (x0)′P0x0.In particular,if x0=0,then J(v;0,0)≥0,which is equivalent to‖L‖ ≤ γ.To show ‖L‖ ＜ γ,we define an operator

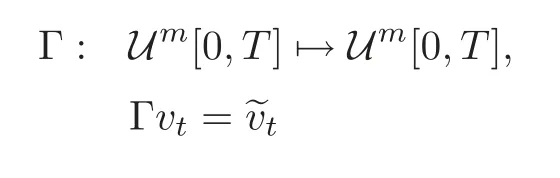
with its realization

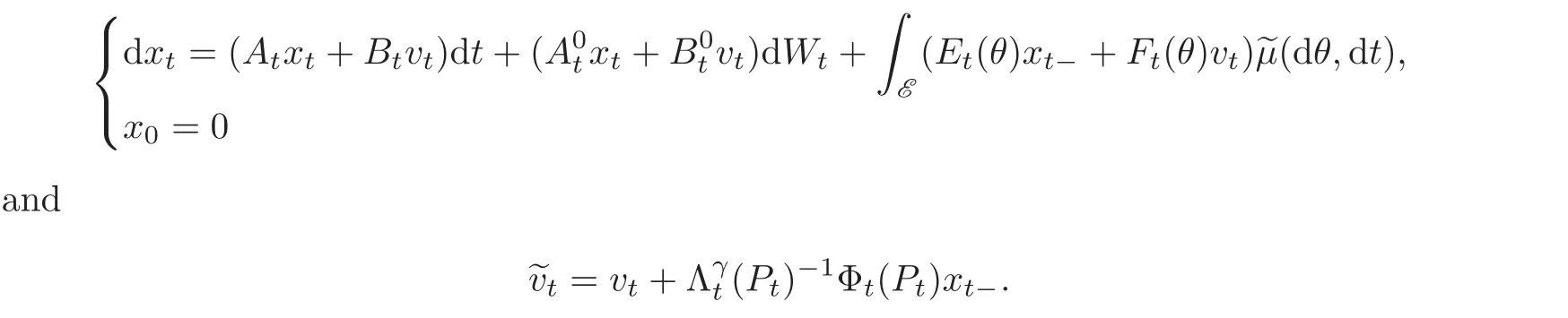
According to the estimate for SDE(2.2),we conclude that the operator Γ is well defined,moreover,it is a bounded linear operator.Then Γ−1exists,which is determined by

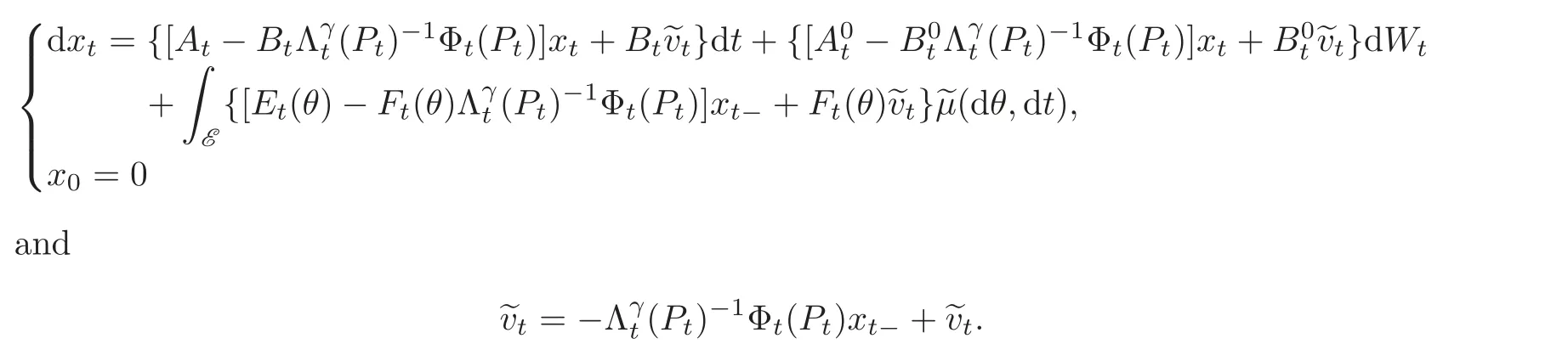
Based on the inverse operator theorem in functional analysis,‖Γ−1‖ is bounded.There exists a positive constantsuch that

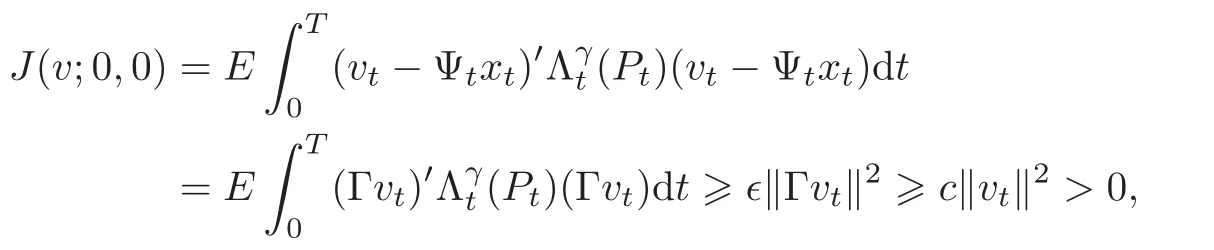
which is equivalent to‖L‖＜γ.This proposition is proved.

The preceding proposition implies that for any given γ＞0,as long as the SRE(3.4)is solvable,the worst effect of the unknown disturbance v on the to-be-controlled output z can be controlled below γ.

In order to prove the second part of the SBRL,Theorem 3.1,we proceed by parts, first establishing some intermediate results.

Using the notation in(3.5),we set

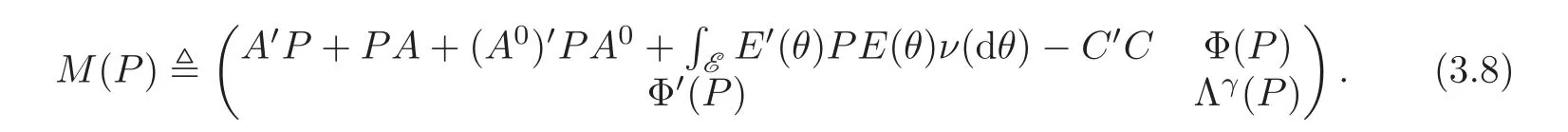
The next result provides an alternative form of writing up the functional defined in(3.3).This new way of expressing the cost allows us to solve the aforementioned minimization problem in a rather straightforward manner.

Lemma 3.1 Suppose that P:is continuously differentiable.Then for every ξ∈,v ∈[τ,T],

where M(P)is defined by(3.8)and x is the solution to the state equation of system(3.1).

Proof Applying It’s formula(2.1)to 〈xt,Ptxt〉,and noting that

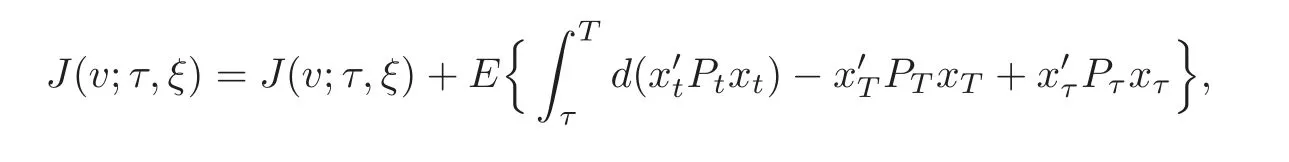
we can easily obtain the result.

Lemma 3.2 Suppose that ϕ ∈ C(τ,T;Rm×n)and Pγ,ϕsatisfy the linear differential matrix equation

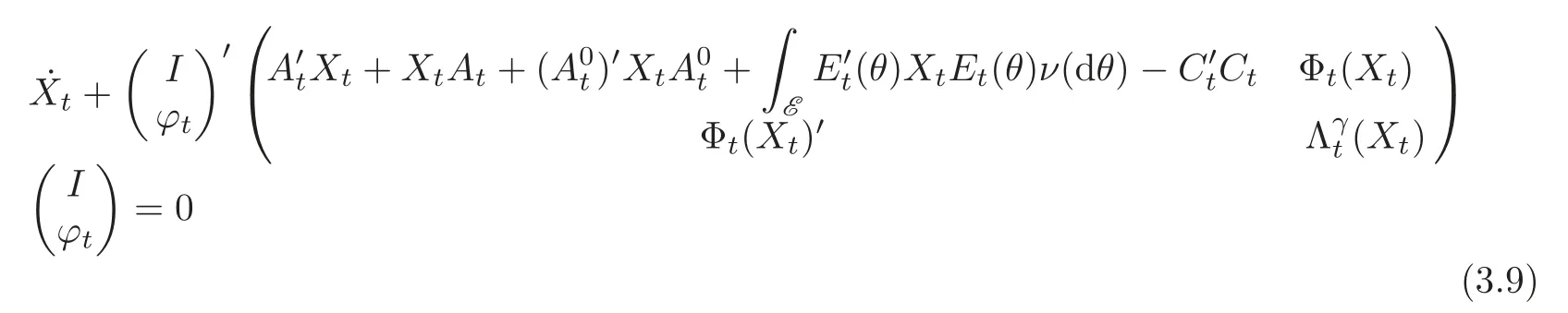
with=0.Then if v ∈ Um[τ,T],we have

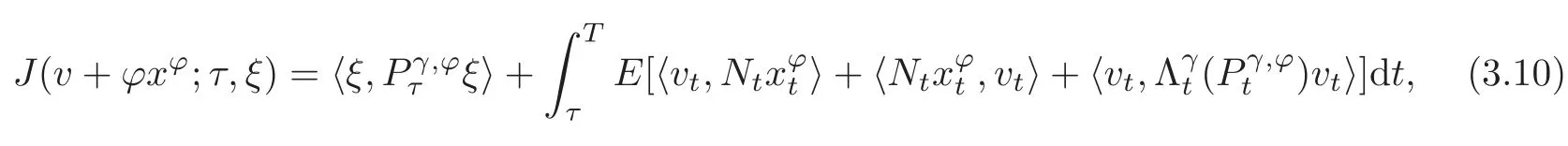
where xϕ=x(·,v+ ϕxϕ;τ,ξ)is the solution of

andIn particular,if v=0,then

Proof As Pγ,ϕsatisfies

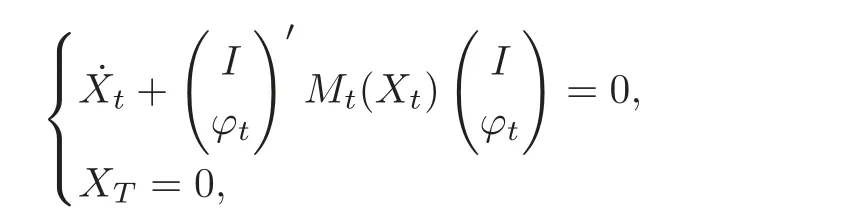
applying Lemma 3.1 with P=Pγ,ϕand v+ϕxϕfor v,we obtain

Hence,(3.10)holds.Setting v=0 in(3.10),we obtain(3.12).The lemma is proved.

In the proof of last lemma,we should notice that as all the coefficients of(3.11)are continuous and uniformly bounded,from Lemma 2.2,there exists a unique solution xϕ∈(τ,T;Rm)to the equation.Hence,ϕxϕ∈(τ,T;Rm).Therefore,v+ ϕxϕ∈ Um[τ,T]holds true.

The following lemma establishes a lower bound for the cost functional,which depends only on the norm of the initial state.

Lemma 3.3 Suppose ‖L‖ ＜ γ.Then there exists μ ＞ 0,such that for any(τ,ξ)∈ [0,T]×Rnand any v ∈ Um[τ,T],we have J(v;τ,ξ)≥ −μ|ξ|2.

Proof Denote by X the solution of(3.9)with ϕ≡0 and final value XT=0,i.e.,X solves

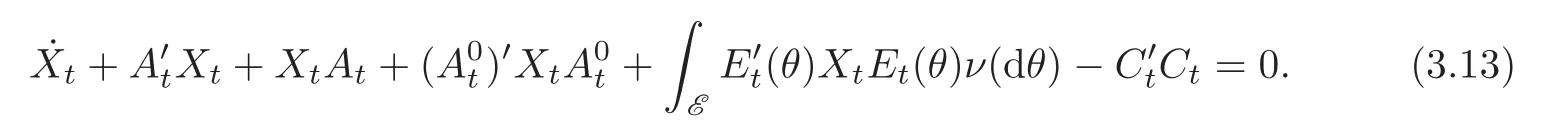
By linearity,the solution x(t,v;τ,ξ)of(3.1)satisfies

Applying(3.10)with ϕ=0,we get

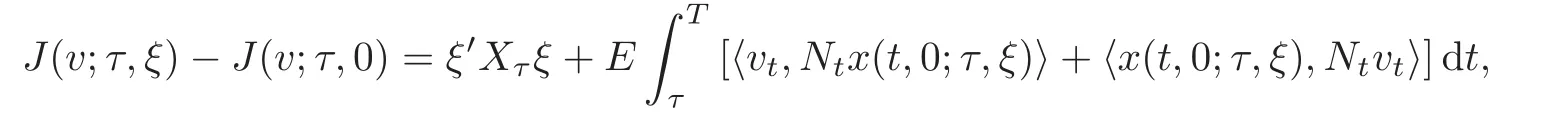
where Nt=(Xt).Let 0＜ ∈2≤ γ2− ‖L‖2,then

We can easily deduce that J(v;τ,0) ≥ ∈2‖v‖2for all v ∈ Um[τ,T].Hence

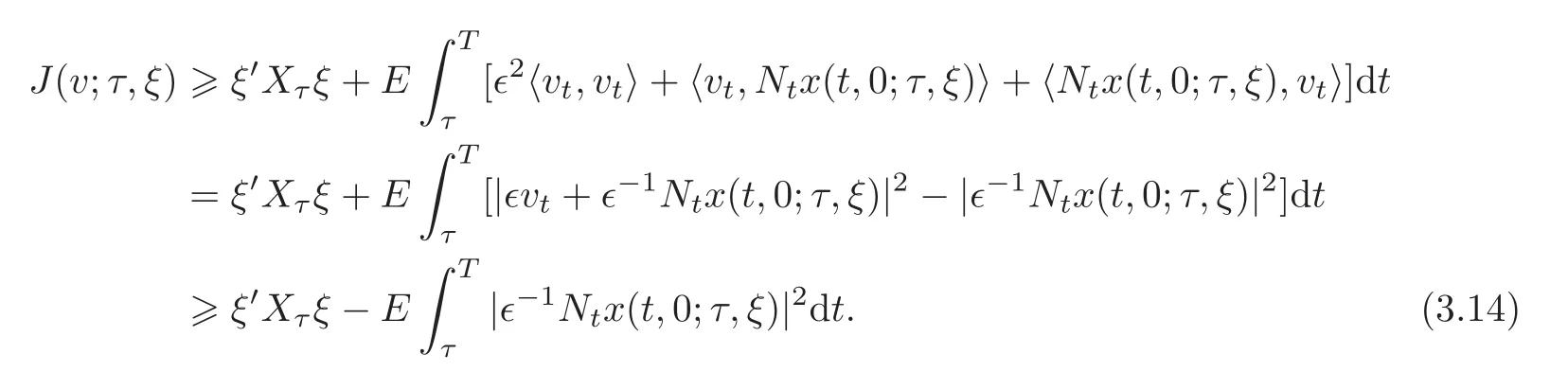
According to the estimate for SDE(2.2),there exists c0＞0 such that

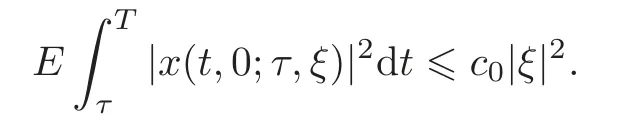
Hence,by(3.12)there exist constants c1,c2＞0 such that

Thus,by(3.14),

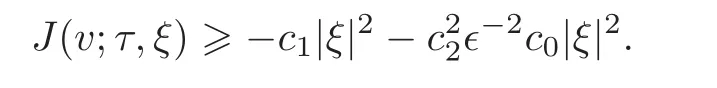
This lemma is proved.

Lemma 3.4 Suppose that ‖L‖ ＜ γ, ϕ ∈ C(τ,T;Rm×n),and Pγ,ϕsatisfies(3.9)withThen

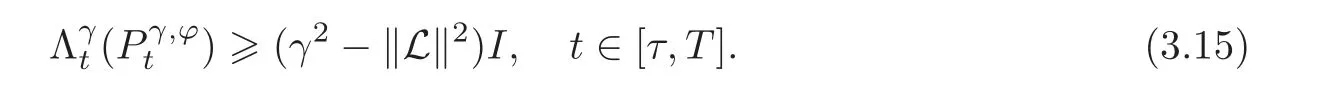
Proof We will first prove thatSuppose that this is false and there existssuch thatfor some η ＞0.Assume＜T.Then,for δ＞ 0 sufficiently small,

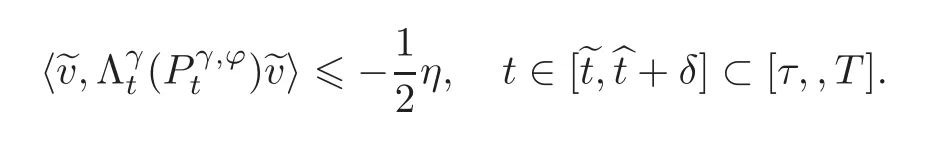
Define

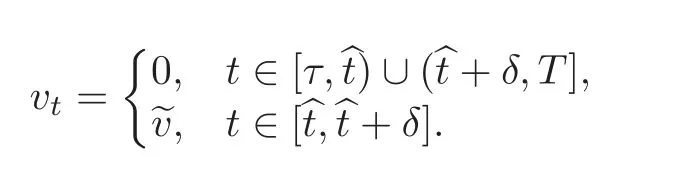
Let τ=0, ξ=0.Then by a prior estimate(2.2),we have

i.e.,Particularly,Now applying Lemma 3.2 to the aforementioned v,we have

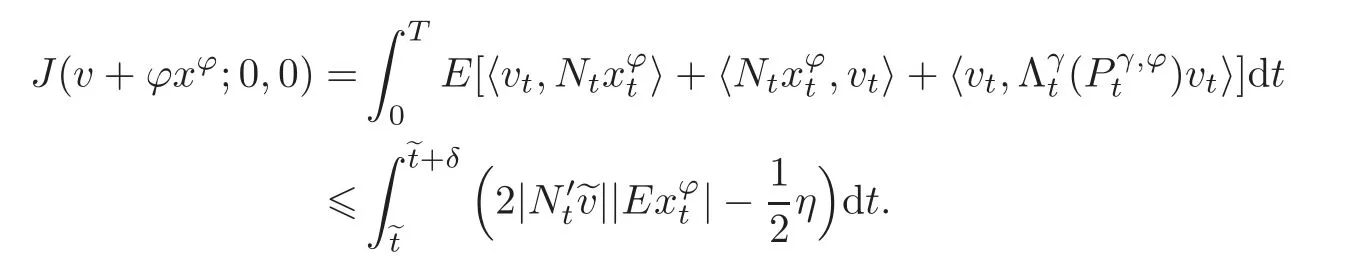
Choosing δ＞ 0 sufficiently small,the integrand becomes negative,sinceis right continuous and=0.While by Lemma 3.3,we have

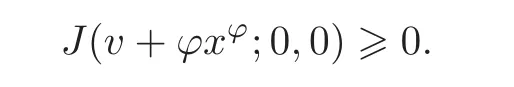
This yields a contradiction whenceIf=T,a similar proof applies,replacing the interval

Now let∈be any positive number such that‖L‖2＜ γ2− ∈2.Applying the previous stepinstead of γ we obtain,for the corresponding solutionof(3.9)(withinstead of γ),By(3.12),we obtain,for any τ∈[0,T)and ξ∈Rn,

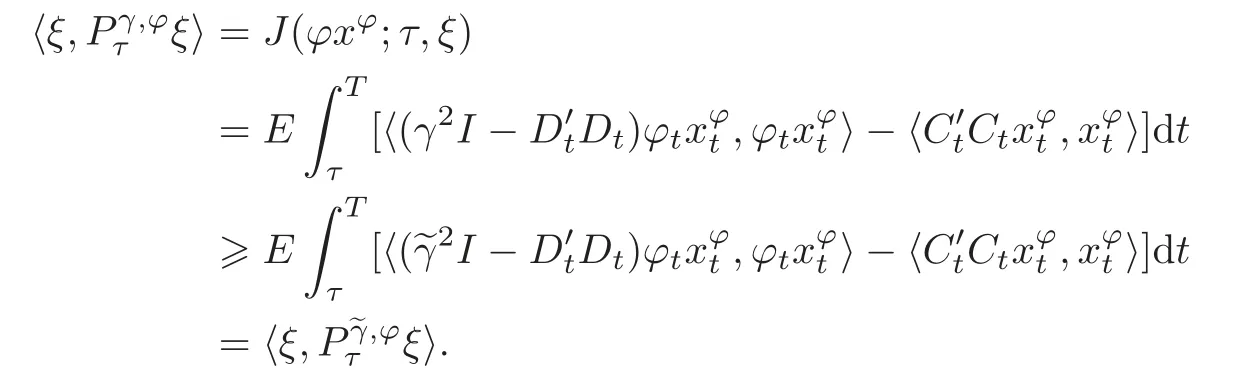
It follows that if γ ＞thenTherefore

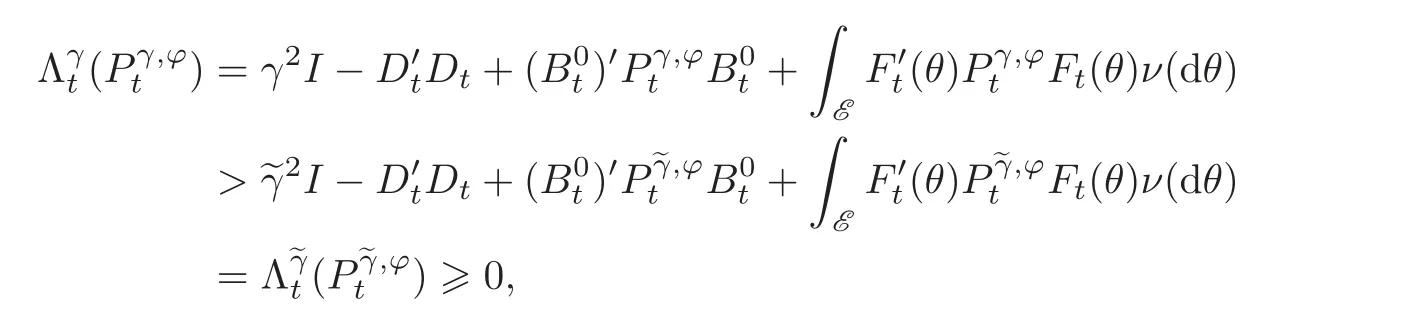
i.e.,for all t∈[0,T].Since this holds for arbitrary∈2＜ γ2−‖L‖2,(3.15)follows.The proof is complete.

We will now study the matrix differential equation(3.4).The function

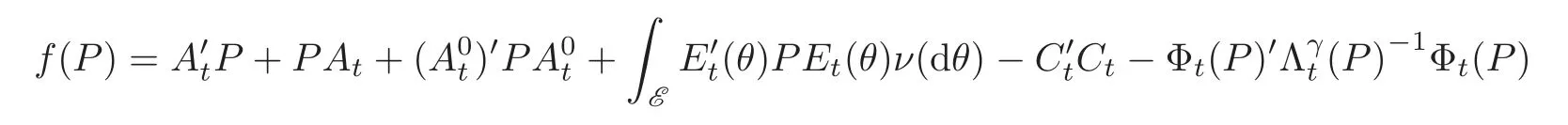
is continuously differentiable on its domain of definition Df={P:det(Λγ(P))0}.From the existence and uniqueness theorem of local solution to ordinary differential equation(ODE for short),there exists a unique solution to(3.4)on[T − δ,T]for sufficiently small δ＞ 0.

We are now in a position to prove the second part of Theorem 3.1,that is,if‖L‖ ＜ γ,SRE(3.4)has a global solution on[0,T].

Proof of Theorem 3.1 It only remains to prove the converse of Proposition 3.2.Assumeholds for every t∈ [0,T].And as PT=0,it follows that for sufficiently small δ＞ 0,

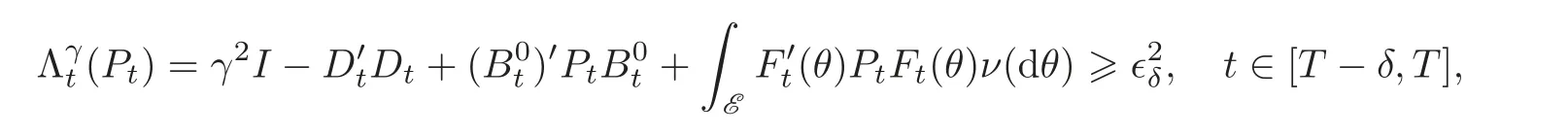
where ∈δis a positive constant depending on δ.Then P is continuously differentiable on[T −δ,T]and the Riccati equation(3.4)has a unique solution P on[T − δ,T].Setting ϕ replaced by Ψ = −Λγ(P)−1Φ′(P)∈ C(T − δ,T;Rn×m)on the left hand side of(3.9),we obtain

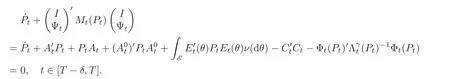
The last equality holds because of the local solvability of(3.4).Hence P satisfies(3.9)on[T − δ,T]with Ψ = ϕ,i.e.,Moreover,with this choice of Ψt,

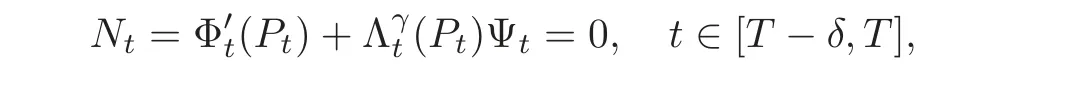
and so Lemma 3.2 implies that,

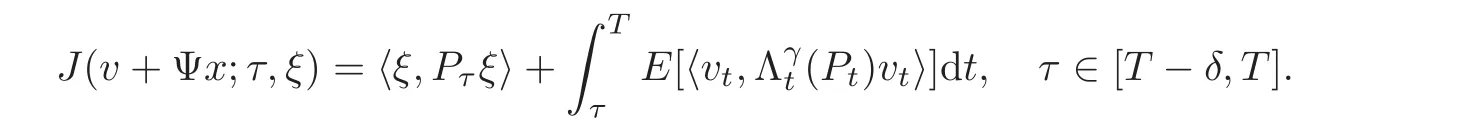
But by Lemma 3.4,

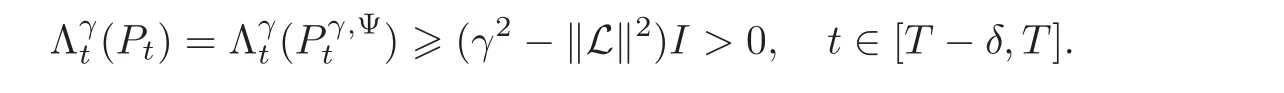
Hence,for all t∈[T−δ,T],the optimal feedback control is

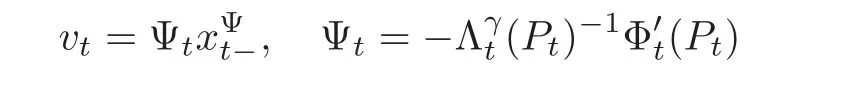
with xΨsatisfying

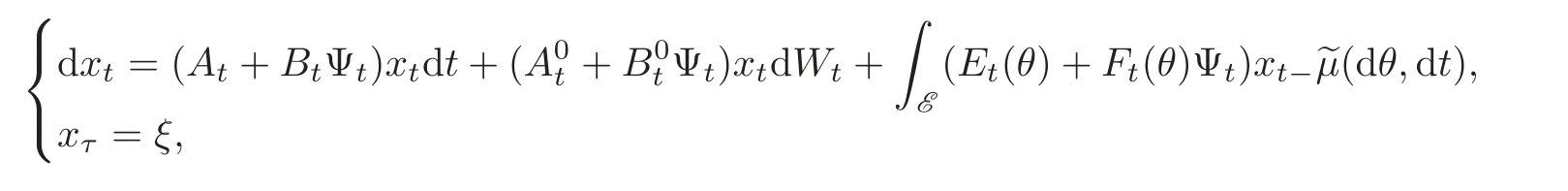
and the optimal cost is

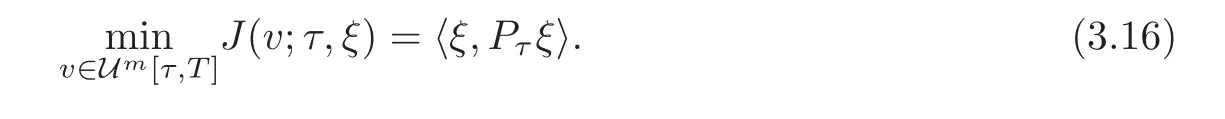
As a consequence,we obtain

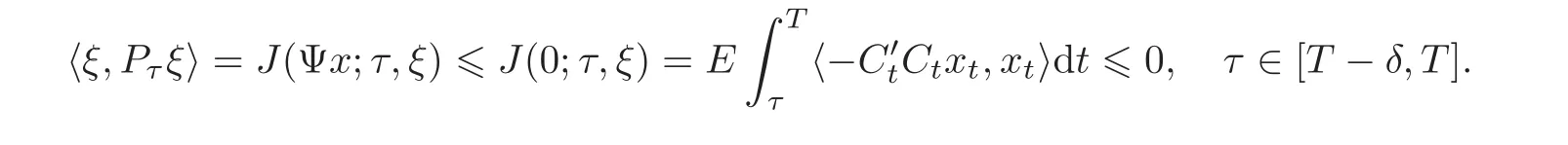
On the other hand,by Lemma 3.3,

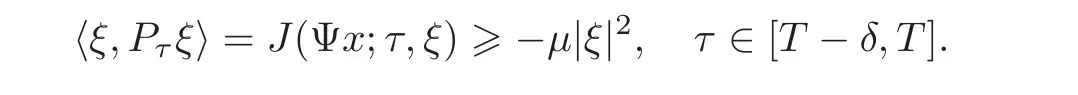
Hence,

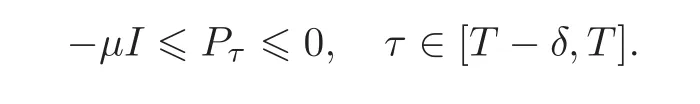
Now,suppose that there exists a solution of(3.4)backwards in time on a maximal interval(σ,T]⊂ [0,T],and as t ↓ σ,Ptbecomes unbounded,i.e.,(3.4)exhibits the phenomenon of a finite escape time.We shall show that the existence of a finite escape time will lead to a contraction.In fact,by the discussion above,the following estimates hold in the interval[σ + σ∈,T]with σ∈＞ 0 sufficiently small:

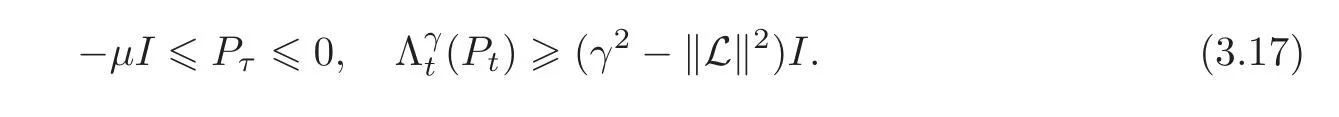
As the constant μ is independent of the left interval endpoint σ + σ∈,letting σ∈↓ 0,we obtain−μI≤Pτ≤0 on(σ,T].Hence,the solution Ptof(3.4)cannot escape to∞ as t↓σ.It follows that there exists a boundary point P0,det(Λγ(P0))=0 of the domain Dfwhich is a limit point of Ptas t ↓ σ.But this contradicts the fact that by(3.17),(Pt) ≥ (γ2− ‖L‖2)I as t↓σ.Thus,the maximal solution interval is[0,T].The uniqueness of the solution follows from(3.16).

The proof of Theorem 3.1 is completed.

So far,we have shown the stochastic bounded real lemma for Poisson jump-diffusion system,that is,‖L‖ ＜ γ is equivalent to that the SRE(3.4)has a unique negative semi-definite solution.Theoretically,by virtue of this theorem,the in fi mum of all these given disturbance attenuation levels γ＞0 such that the corresponding SRE(3.4)has a unique solution,can be used as an estimate of‖L‖.

4 Stochastic H2/H∞ Control for Jump-Diffusion Systems

In this section,we shall give necessary and sufficient conditions for the solvability of the stochastic H2/H∞control problem in terms of four cross-coupled Riccati equations.

Consider the stochastic linear system(2.3),the finite horizon stochastic H2/H∞control problem can be stated as follows.

Definition 4.1 Given a disturbance attenuation level γ＞0,to find,if possible,a state feedback control u∗∈ Us[0,T],such that with the constraint(2.3),we have that

(1)

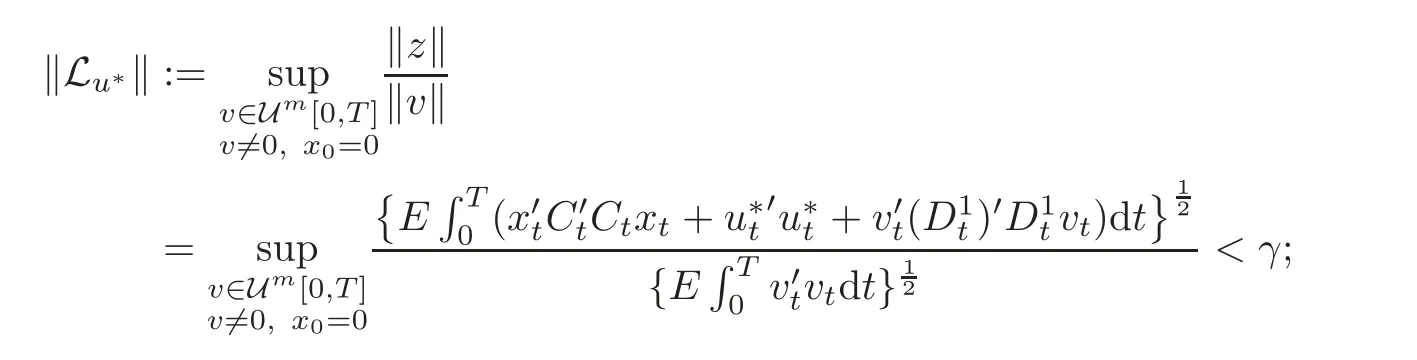
(2)when the worst case disturbance v∗∈ Um[0,T],if it exists,is applied to the system(2.3),u∗minimizes the output energy

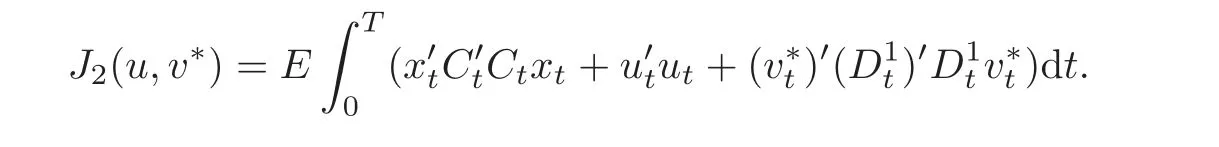
Here,the so-called worst case disturbance v∗means that for any v∈ Um[0,T]and any x0∈Rn,

If the previous(u∗,v∗)exists,then the finite horizon H2/H∞control has a pair of solutions(u∗,v∗).

The following lemma,which is necessary in the derivation that follows,is given without proof and its proof can be analogous to that of Theorem 7.2 of[25].

Lemma 4.1 Riccati equation

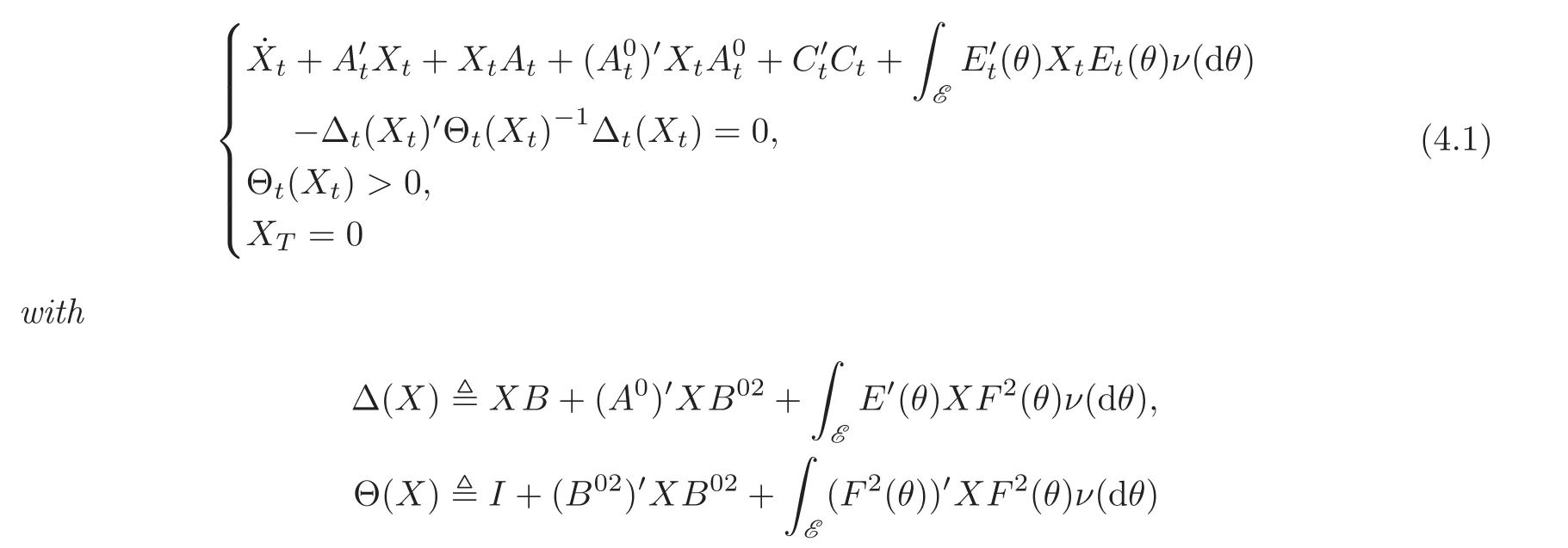
admits a unique solution X.Moreover,X is semi-positive definite and uniformly bounded.

Remark 4.1 In view of the relationship between the Riccati equation(4.1)and the linear quadratic(LQ for short)optimal control problem,where the dynamic system is driven by:

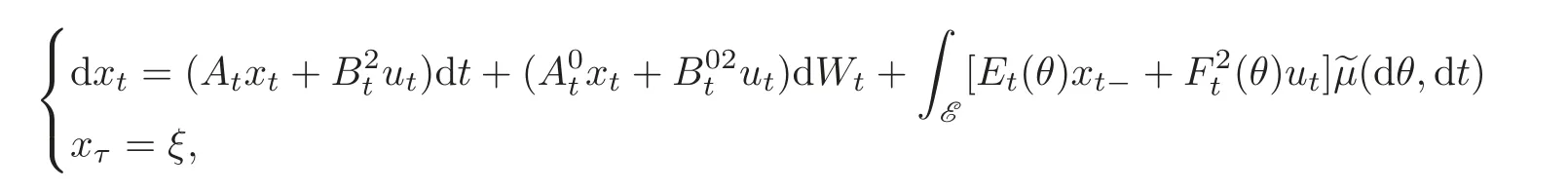
and the corresponding cost functional is

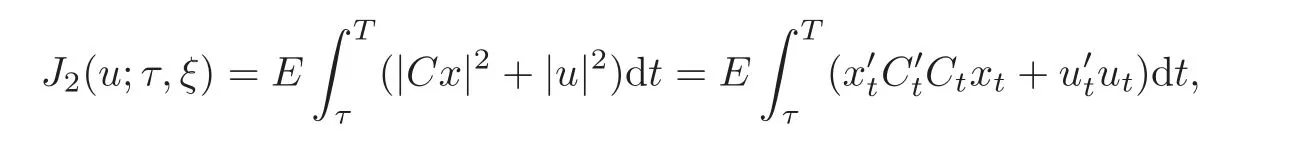
we immediately obtain that the optimal feedback control is

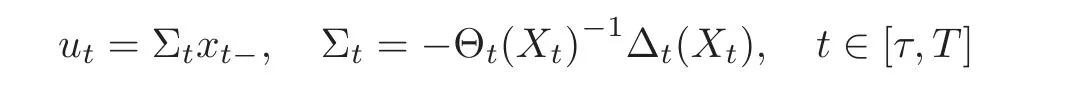
with xtsatisfying

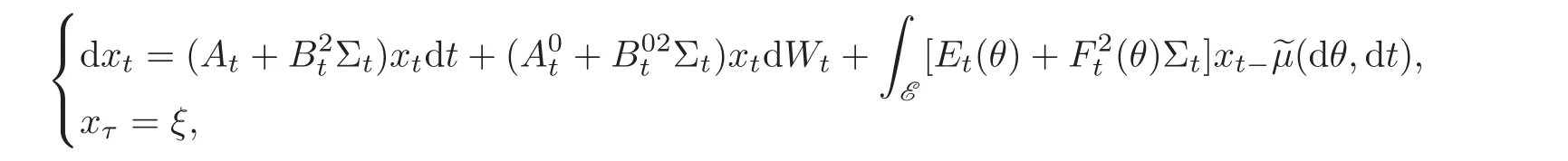
and the optimal cost iswhere X is the solution to(4.1).

In the following,we shall give sufficient and necessary conditions for the existence of the linear state feedback pair(u∗,v∗),which generalize the result of Chen and Zhang[2]to the case of stochastic systems with Poisson random jumps and(x,u,v)-dependent noise.

For convenience,we introduce the following notation:

Theorem 4.1 For stochastic system(2.3),if the following four coupled matrix Riccati equations

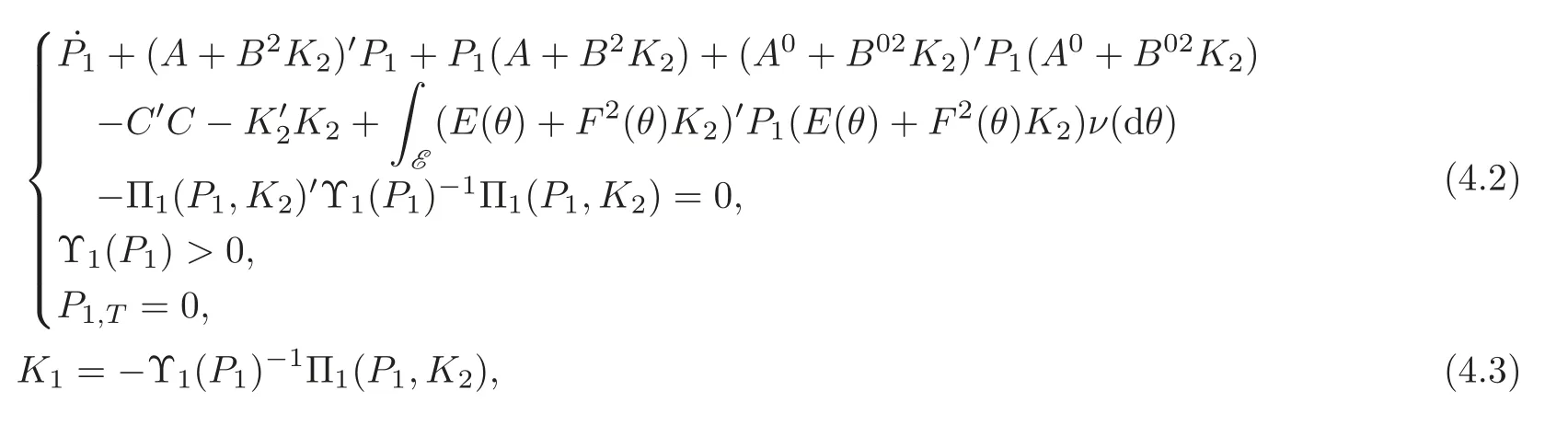
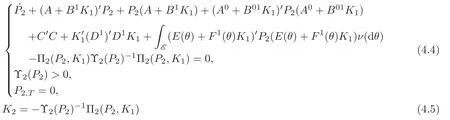
have solutions(P1,P2,K1,K2)with P1≤0 and P2≥0,then the H2/H∞control problem admits a pair of solutions(u∗,v∗)satisfying

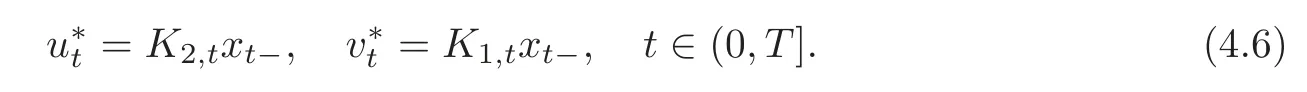
Moreover,setting x0=0 and u=u∗,‖Lu∗‖ ＜ γ for any v ∈ Um[0,T].

Proof Suppose that the coupled matrix Riccati equations(4.2)–(4.5)are solvable.Let us consider the cost functional J1(u,v) first.Applying It’s formula(2.1)and completion of squares,we have

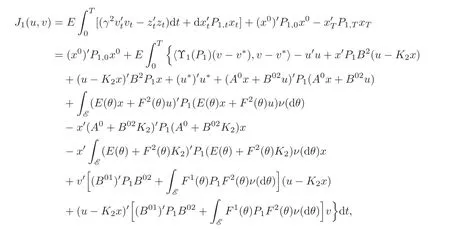
where u∗and v∗are determined by(4.6).Setting u=u∗=K2x,we obtain

Therefore,J1(u∗,v∗)≤ J1(u∗,v)and J1(u∗,v∗)=(x0)′P1,0x0,which implies that v∗is the worst case disturbance corresponding to u∗.A similar method as Proposition 3.1 yields ‖Lu∗‖ ＜ γ.Similarly,

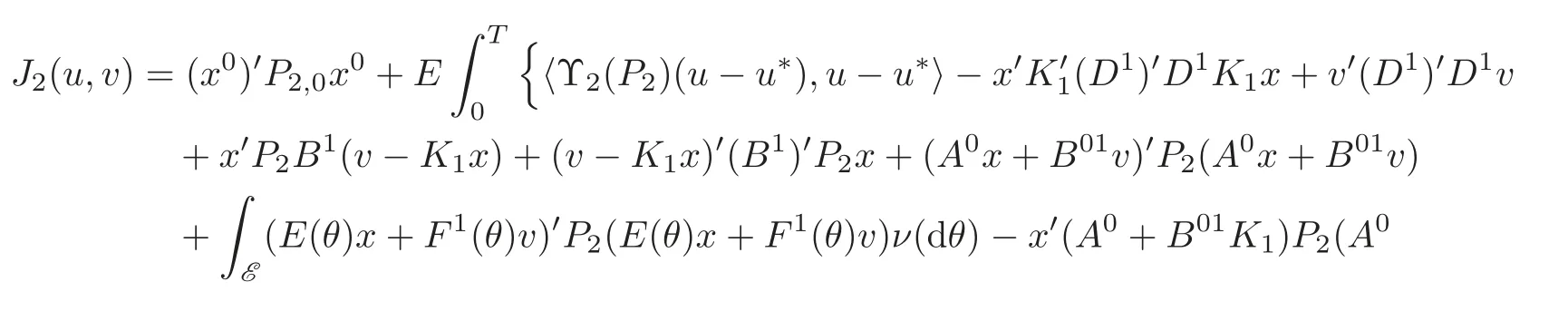
and setting v=v∗results in J2(u∗,v∗) ≤ J2(u,v∗)and J2(u∗,v∗)=(x0)′P2,0x0.The above information implies that the finite horizon H2/H∞control has a pair of solutions(u∗,v∗)with u∗and v∗defined in(4.6).

We establish the signs of P1,tand P2,tas follows.

(i)A completion of squares argument similar to that which led to(4.7),together with setting u=u∗and v=v∗,we finally obtain

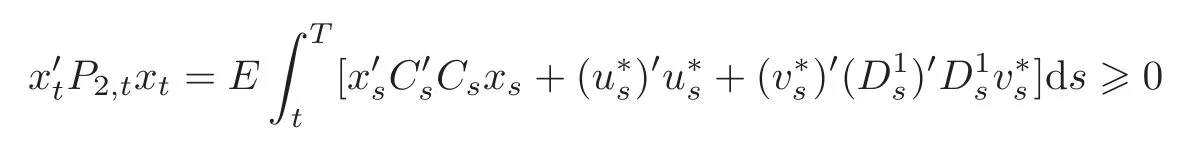
for arbitrary xt.Consequently,P2,t≥0 for all t∈[0,T].

(ii)A similar calculation using J1(·,·)with u=u∗and v=0 gives

Thus P1,t≤0 for all t∈[0,T].The proof is complete.

Theorem 4.2 Assume that the finite horizon H2/H∞control problem admits a pair of linear state feedback solutionswhereandare continuous matrix-valued functions on[0,T].Then the coupled matrix Riccati equations(4.2)–(4.5)have a unique quaternion solution(P1,P2,G1,G2)with P1≤ 0 and P2≥ 0.

Proof If(u∗,v∗)is the solution of the considered H2/H∞control problem,then we will prove that the matrix-valued equations(4.2)–(4.5)are solvable.

(I)Implementingin(2.3)with G2to be determined,we obtain

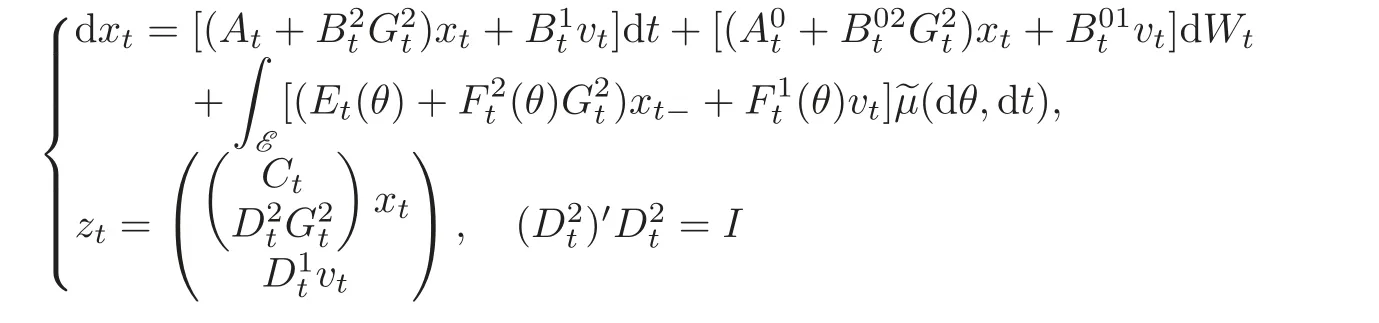
with xτ= ξ.Since the finite horizon H2/H∞control is solvable,by definition 4.1,‖Lu∗‖ ＜ γ.Hence,according to Theorem 3.1,Riccati equation

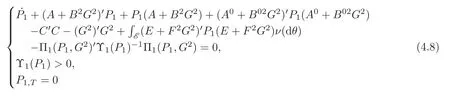
has a unique solution P1≤0.Moreover,the optimal control problem

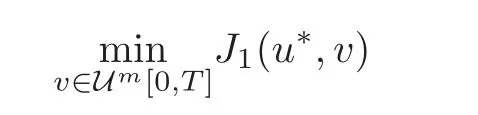
has a unique solution

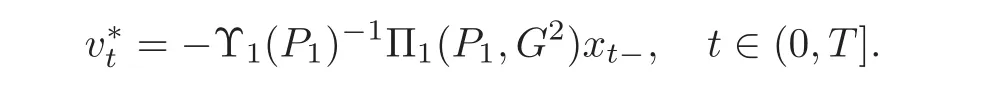
Hence

(II)Substitutinginto(2.3)with G1being defined as(4.9),we obtain

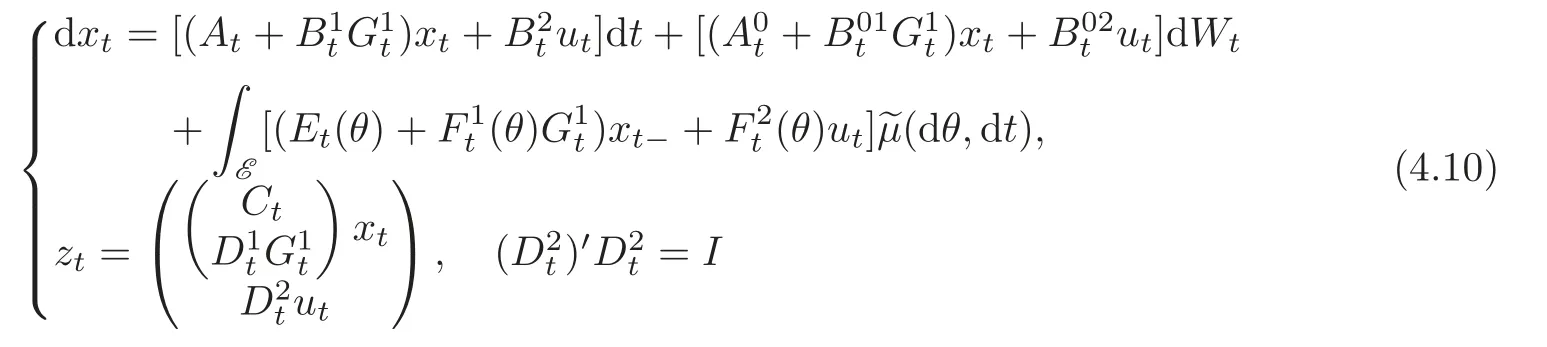
with xτ= ξ.Since

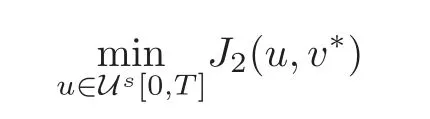
is a standard stochastic linear quadratic optimal control problem,according to Remark 4.1,there exists a unique optimal control

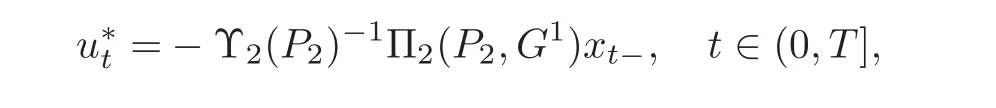
where P2≥0 solves

Hence

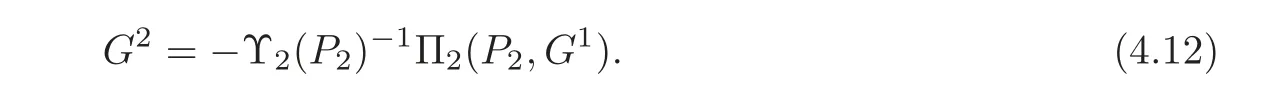
Therefore,the coupled matrix-valued equations(4.2)–(4.5)have a unique quaternion solution(P1,P2,G1,G2)with P1≤0 and P2≥0.The proof is complete.

The last two theorems imply that for the stochastic linear system(2.3),the existence of a state feedback stochastic H2/H∞control is equivalent to the solvability of the four coupled Riccati equations(4.2)–(4.5).As it is generally difficult to solve the aforementioned four coupled equations,we will present a discretization technique.Set h=for a natural number n＞0,and denote ti=ih with i=0,1,2,···,n.When n is sufficiently large,or equivalently,when h is sufficiently small,we may replace(4.2)and(4.4),respectively.Then a backward recursive algorithm can be given as follows:

(i)By solving(4.3)and(4.5),it follows K1,T=0,K2,T=0 from given terminal condition P1,T=0,P2,T=0.

(ii)Solving(4.2)and(4.4)yields P1,tn−1=P1,T−h=−CT≤0 and P2,tn−1=P2,T−h=CT≥0.

(iii)Repeating above steps(i)–(ii),P1,ti,P2,timay be computed if P1,ti+1≤ 0 and P2,ti+1≥ 0 are available with

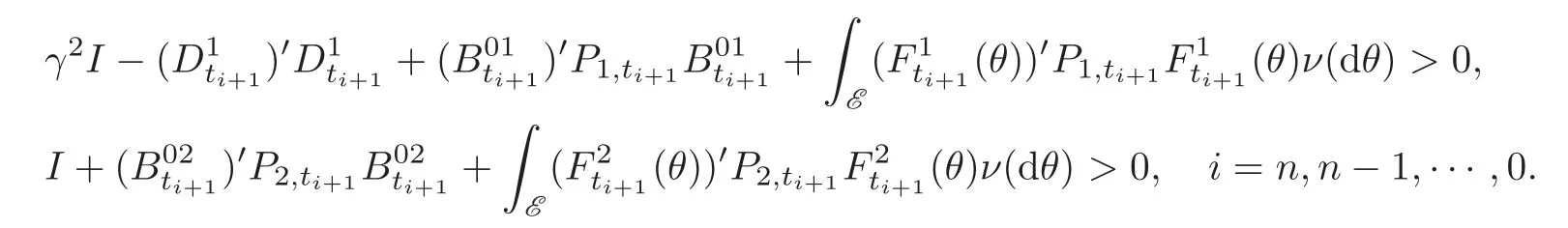
The above recursions may proceed for even if P1,ti≤0,P2,ti≥0 and

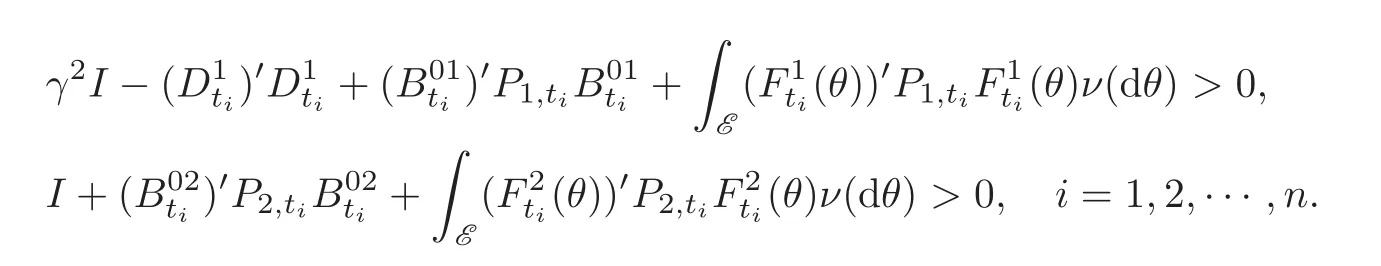
Because if the coupled Riccati equations(4.2)–(4.5)admit a quaternion solutionmust be uniformly continuous on[0,T].Therefore,we have

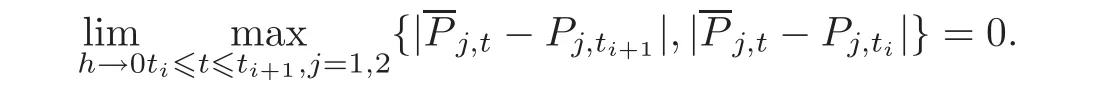
In particular,for some special systems,we may solve(4.2)–(4.5)analytically,see the following example.

Example 4.1 Consider the one-dimensional linear stochastic system with jumps as follows:

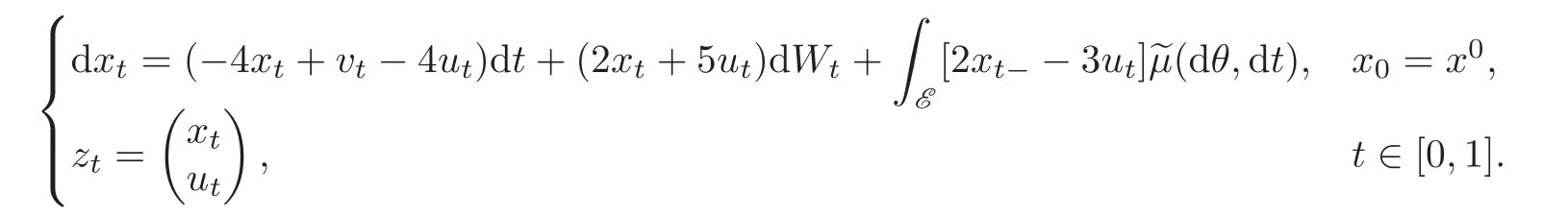
If we take γ =1 and ν(E)=1,then the coupled Riccati equations(4.2)–(4.5)specialize to

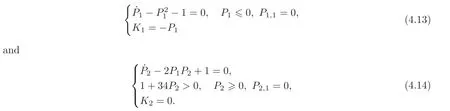
Solving in turn(4.13)–(4.14),yields

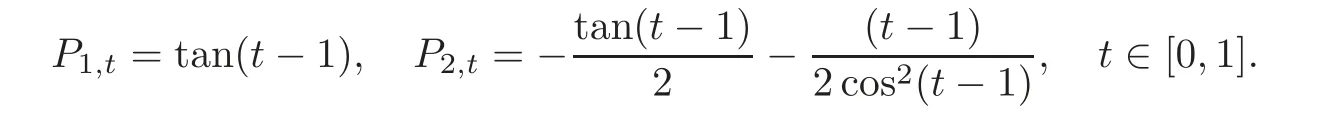
Therefore,our desired H2/H∞controller and worst case disturbance are=0 and=−tan(t− 1)xt−respectively,where x satisfies

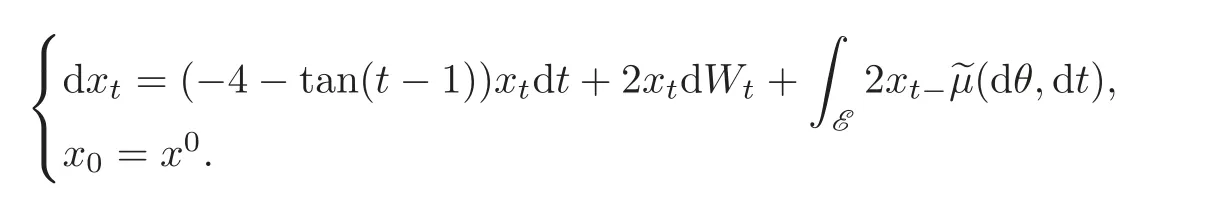
5 Concluding Remarks

This paper has discussed the finite horizon H2/H∞control problem for Poisson jumpdiffusion systems with(x,u,v)-dependent noise.Necessary and sufficient conditions for the existence of a state feedback H2/H∞control have been respectively given in terms of the solutions of the four coupled matrix Riccati equations.A discretization algorithm for solving the coupled matrix-valued equations is also presented.It is noteworthy that the stochastic bounded real lemma is of independent interest and plays a central role in the analysis of the H∞control problem(in fact a disturbance attenuation problem)and estimation.Its further applications will appear in our forthcoming paper.There remain many interesting topics deserving further explorations.For example,for Poisson jump-diffusion systems with control dependent noise and random coefficients,the corresponding Riccati equation associated with H∞robustness becomes a backward stochastic integral partial differential equation with highly nonlinearity and possible singularity,whose solvability is a challenging problem and deserves for further study.

AcknowledgementThe author is deeply grateful for the comments and suggestions provided by the referees.

[1]Boel,R.K.and Varaiya,D.,Optimal control of jump processes,SIAM J.Contr.Optim.,15(1),1977,92–119.

[2]Chen,B.and Zhang,W.,Stochastic H2/H∞control with state-dependent noise,IEEE Trans.Automat.Contr.,49(1),2004,45–57.

[3]Chen,W.and Chen,B.,Robust stabilization design for nonlinear stochastic system with Poisson noise via fuzzy interpolation method,Fuzzy Sets Syst.,217,2013,41–61.

[4]Doyle,J.C.,Glover,K.,Khargonekar,P.P.and Francis,B.,State-space solutions to standard H2and H∞problems,IEEE Trans.Automat.Contr.,34,1989,831–847.

[5]Dragan,V.and Morozan,T.,Stability and robust stabilization to linear stochastic systems described by differential equations with Markovian jumping and multiplicative white noise,Stochastic Analysis and Applications,20(1),2002,33–92.

[6]Dragan,V.and Morozan,T.,The linear quadratic optimization problems for a class of linear stochastic systems with multiplicative white noise and Markovian jumping,IEEE Trans.Automat.Contr.,49(5),2004,665–675.

[7]Dragan,V.,Morozan,T.and Stoica,A.,Mathematical Methods in Robust Control of Discrete-Time Linear Stochatic Systems,Springer-Verlag,New York,2010.

[8]Framstad,N.,Oksendal,B.and Sulem,A.,Optimal consumption and portfolio in a jump diffusion market with proportional transaction costs,J.Math.Econ.,35(2),2001,233–257.

[9]Gihman,I.I.and Skorohod,A.V.,The Theory of Stochastic Processes III,translated from the Russian by Kotz,S.,Springer-Verlag,Berlin,1979.

[10]Hinrichsen,D.and Pritchard,A.J.,Stochastic H∞,SIAM J.Contr.Optim.,36(5),1998,1504–1538.

[11]Hou,T.,Zhang,W.and Ma,H.,In finite horizon H2/H∞optimal control for discrete-time Markov jump systems with(x,u,v)-dependent noise,J Glob.Optim.,57,2013,1245–1262.

[12]Ikeda,N.and Watanabe,S.,Stochastic Differential Equations and Diffusion Processes,North-Holland Publishing Company,Amsterdam,1981.

[13]Khargonekar,P.P.and Rotea,M.A.,Mixed H2/H∞control:A convex optimization approach,IEEE Trans.Automat.Contr.,36(7),1991,824–837.

[14]Limebeer,D.J.N.,Anderson,B.D.O.and Hendel,B.,A Nash game approach to mixed H2/H∞control,IEEE Trans.Automat.Contr.,39(1),1994,69–82.

[15]Lin,Z.,Lin,Y.and Zhang,W.,A unified design for state and output feedback H∞control of nonlinear stochastic Markov jump systems with state and disturbance-dependent noise,Automatica,45(12),2009,2955–2962.

[16]Lin,X.and Zhang,R.,H∞control for stochastic systems with Poisson jumps,J.Syst.Sci.Complex,24(4),2011,683–700.

[17]Merton,R.C.,Option pricing when underlying stock returns are discontinuous,J.Financial Econ.,3,1976,125–144.

[18]Situ,R.,Option pricing in mathematical financial market with jumps and related problems,Vietnam J.Math.,30(2),2002,103–122.

[19]Sweriduk,G.D.and Calise,A.J.,Differential game approach to the mixed H2/H∞problem,Journal of Guidance Control and Dynamics,20,1997,1229–1234.

[20]Tang,S.and Li,X.,Necessary condition for optimal control of stochastic systems with random jumps,SIAM J.Contr.Optim.,32(5),1994,1447–1475.

[21]Todorov,M.G.and Fragoso,M.D.,In finite Markov jump-bounded real lemma,Systems and Control Letters,57,2008,64–70.

[22]Todorov,M.G.and Fragoso,M.D.,A new perspective on the robustness of Markov jump linear systems,Automatica,49,2013,735–747.

[23]Wang,M.,Stochastic H2/H∞control with random coefficients,Chin.Ann.Math.Ser.B,34,2013,733–752.

[24]Yan,H.and Liu,S.,Pricing options on stocks driven by Poisson jump-diffusion process,J.Engineering Mathematics,20,2003,35–40.

[25]Yong,J.and Zhou,X.,Stochastic Controls:Hamiltonian Systems and HJB Equations,Springer-Verlag,Berlin,New York,1999.

[26]Zhang,W.and Chen,B.,State feedback H∞control for a class of nonlinear stochastic systems,SIAM J.Contr.Optim.,44(6),2006,1973–1991.

[27]Zhang,W.,Zhang,H.and Chen,B.,Stochastic H2/H∞control with(x,u,v)-dependent noise:Finite horizon case,Automatica,42,2006,1891–1898.