利用小普查数据对“随机婚配”假定的再检验

摘 要：使用2005年人口小普查数据研究了独生子女之间的婚配选择问题，发现独生子女更可能与独生子女结婚，且非独生子女也更可能与非独生子女结婚，所以认为独生子女与非独生子女之间“随机婚配”的假定并不符合实际。然而，以往有关生育政策调整的人口预测大都基于这一假定之上，这导致预测结果一方面低估了“双独”和“双非”夫妇的数量，另一方面高估了“单独”夫妇的数量。同时，本文还以独生子女的婚配选择问题为例讨论了嵌套模型中Logistic回归系数的可比性问题。直接比较Logistic回归系数可能导致错误的结论，借助“y*标准化”法和“KHB分解法”可以在一定程度上解决Logistic回归系数不可比的问题。

关键词：2005年小普查数据；独生子女；“随机婚配”假定；Logistic回归系数

中图分类号：C92-05 文献标识码：A 文章编号：1000-4149（2016）03-0043-09

Abstract：Based on the 2005 minicensus data， this paper studies the mating selection problem of only child under the age of 30 and finds that only child is more likely to marry only child and that people with siblings are more likely to marry people with siblings. Therefore， the “Random Mating” hypothesis is far beyond the truth. However， the previous studies concerning fertility policy adjustment were all based on this hypothesis， which probably underestimated the quantity of couples that both/neither are only child and overestimated the quantity of couples that either is only child. Taking the mating selection problem of only child for example， this paper also discusses the comparability of coefficients of nested Logistic regression and points out that direct comparison of the coefficients of nested Logistic models will result in incorrect conclusion. “y* standardization” and “KHB decomposition” are two methods that can resolve the incomparability problem of the coefficients of nested Logistic regressions.

Keywords：2005 minicensus data； only child； “Random Mating” hypothesis； coefficient of Logistic regression

一、导论

中国的计划生育政策，特别是30 多年来独生子女政策的全面推行不仅产生了数以亿计的独生子女[1]，而且创造了“双独”、“单独”和“双非”

“双独”夫妇指夫妇双方均为独生子女；“单独”夫妇指夫妇中只有一方是独生子女；“双非”夫妇指夫妇双方都不是独生子女。等独具中国特色的夫妇类型[2]。研究这些夫妇类型一方面有助于我们辨识一些特殊的家庭结构（如“四二一”家庭结构），另一方面也有助于当前和未来生育政策的制定（如“双独二孩”政策和“单独二孩”政策都以夫妇双方是否是独生子女为条件）。所以，研究“双独”、“单独”和“双非”夫妇的数量、结构及其在未来的发展趋势是关系到家庭养老和生育政策调整等一系列重大决策的重要问题。

郭志刚等学者曾对这些问题进行过研究，但在研究时面临的一个技术难题是如何确定独生子女之间的婚配概率[3]。由于缺乏相关的数据资料，他们假定年轻人在择偶时不会刻意选择配偶的独生属性，即：假定独生子女和非独生子女之间的婚配是完全随机的（以下简称“随机婚配”假定）。虽然后来有学者对这个假定提出过质疑，但是由于缺乏充分的数据资料，“随机婚配”假定一直沿用至今，并成为后续研究者预测“四二一”家庭结构、“单独”和“双独”夫妇数量的前提和基础[4-7]。但正如该假定的提出者郭志刚等人所指出的，“随机婚配”假定实则是在没有其他更好替代方案情况下的一个无奈之举，而一旦这个假定条件不能得到满足，则很有可能低估“双独”夫妇、“双非”夫妇和“四二一”家庭的数量，并高估“单独”夫妇的数量，从而影响相关政策的制定[3]。

为了检验该假定是否合理，郭志刚和许琪曾使用2010年中国家庭追踪调查数据研究了独生子女的婚配选择问题。他们发现独生子女更可能与独生子女结婚，且非独生子女也更可能与非独生子女结婚，所以“随机婚配”假定并不成立[8]。此后，宋健使用2009年中国城市青年调查数据又对该假定进行了检验，并得到了相同的结论[2]。但由于这两项研究的样本量都较小，其可靠性仍然存在争议。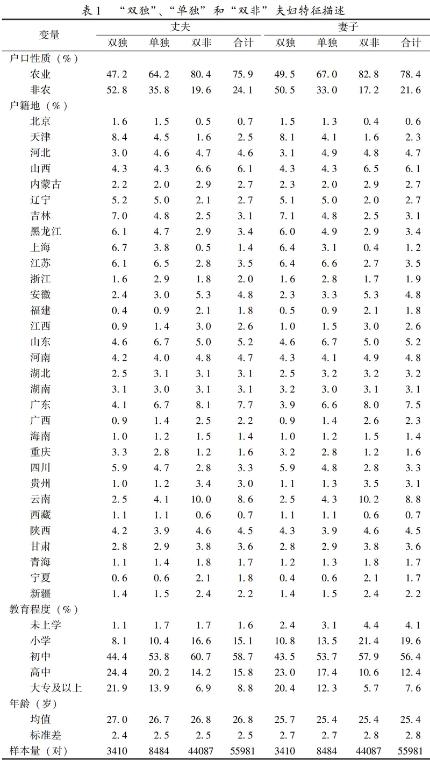

本研究的主要目的是使用2005年小普查这一样本量更大、权威性更强的数据对“随机婚配”假定进行再检验。在研究时，我们还以独生子女的婚配选择问题为例讨论了嵌套模型中Logistic回归系数的可比性问题。虽然Logistic回归模型已经在社会科学领域得到了非常广泛的应用，但它的系数比较问题并未引起国内学者的足够重视。本文以一个实例说明直接比较Logistic回归系数时可能导致的错误，并提出了两种可行的解决方案。这对其他基于Logistic回归的学术研究同样具有指导意义。

二、数据和变量

本研究使用的是2005年全国1%人口抽样调查（也称人口小普查）数据

实际使用的数据的抽样比约为1/500。与历次人口普查和抽样调查数据不同的是，2005年调查登记了30岁及以下人口是否有兄弟姐妹，据此可以判断其是否为独生子女。

分析时，我们首先将样本限定为居住在家庭户中的在婚人口，然后根据同一户中的家庭成员关系对夫妻进行匹配。如果夫妻双方都为初婚，我们还根据双方填报的初婚年是否一致对数据进行校验，并删除初婚年不一致的样本。最后，我们保留双方年龄都在30岁及以下的夫妇（56118对）；在删除缺失值以后，进入分析的夫妇对数为55981对。

分析的核心变量是夫妇双方的独生属性，据此可以判断夫妇所属的类型。如果夫妇双方都为独生子女，即为“双独”夫妇；如果仅有一方为独生子女，即为“单独”夫妇；如果双方都不是独生子女，即为“双非”夫妇。样本中，“双独”、“单独”和“双非”夫妇的数量分别为3410对、8484对和44087对，所占比例分别为6.1%、15.2%和78.7%。

除了夫妇双方的独生属性之外，分析时还考虑了双方的年龄、教育程度、户口性质和户籍地。因为在中国，城乡户籍、籍贯、年龄和教育程度是人们非常看重的四个择偶标准，而且这四重标准都与是否为独生子女密切相关[8]。所以，从这四个维度出发有助于我们探索夫妇在独生子女属性上的关联性。

表1分“双独”、“单独”和“双非”三种类型对夫妇双方的上述特征进行了描述。结果显示，“双独”夫妇中户口为非农的比例明显大于“单独”和“双非”夫妇；且“双独”夫妇的户籍地落在北京、天津、上海等生育政策较严格省份的比例也比其他两类夫妇高；除此之外，“双独”夫妇的教育程度也是三类夫妇中最高的，这都与我们的预期相一致。

不过，表1显示“双独”夫妇的平均年龄是三类夫妇中最高的，这与我们的预期不太相符。因为一般来说，年轻队列中独生子女的比例较高，相应的年轻夫妇中“双独”出现的可能性也较大，所以“双独”夫妇的平均年龄应该比“单独”和“双非”夫妇小。我们认为，出现这种不一致的原因可能在于独生子女结婚普遍比非独生子女晚 这可能是因为独生子女大多出生于城市或相对发达的地区，且教育程度比较高。所以，虽然年轻队列中独生子女的比例较高，但由于结婚晚，“单独”和“双非”夫妇反而比“双独”夫妇显得更加年轻。分析结果显示，15-30岁男性和女性人口中独生子女的比例分别占该年龄段人口的20.2%和17.0%；但在15-30岁在婚人口中，男女独生子女的比例却仅为占该年龄段人口的13.6%和13.7%，而且在越年轻的队列中，二者的差异越大，这就在很大程度上佐证了我们的猜测。与此同时，这一结果也提醒我们在分析时可能需要为不同人群赋予不同的权重，以反映他们在总人口中的构成比例，而加权对数据分析结果的影响我们在下面还将继续讨论。

三、分析结果

1. 双变量列联表分析

为了检验“随机婚配”假定是否成立，我们首先使用双变量的列联表分析了夫妇双方在独生子女属性上的关联性。从表2可以发现，根据夫妻是否独生子女交互分类以后，主对角线上的两个单元格的观测频数都明显大于期望频数 期望频数反映在“随机婚配”条件下应有的结果。而非主对角线上两个单元格的观测频数都小于期望频数。这说明，独生子女更可能与独生子女结婚，且非独生子女也更可能与非独生子女结婚，而独生子女与非独生子女结婚的可能性则相对较小。

经计算，独生子中与独生女结婚的比例为44.7%，而非独生子中与独生女结婚的比例仅为8.8%，二者相差35.9个百分点。

对该比例差的t检验结果非常显著（p<0.000），所以二者的差异是真实存在的。此外，我们还对该列联表的独立性进行了卡方检验，结果也是非常显著的（p<0.000），这就再次拒绝了独生与非独生之间随机婚配的原假设。根据表2计算得到的独生子相对于非独生子与独生女结婚的优势比（odds ratio）为8.35，大大高于1。由此可见，夫妇双方是否为独生子女的关联性是很强的，“随机婚配”假定并不符合实际。

分城乡（见表3）和年龄组（见表4）来看，我们也能得到类似的结论。经计算，城镇和农村的优势比分别为7.95和7.78，25岁以下组和25-30岁组的优势比分别为7.02和8.76，且统计检验结果显示，上述所有优势比都显著大于1。所以，无论在农村还是城市，也无论夫妇的年龄大小，都呈现独生子女更可能与独生子女结婚，而非独生子女更可能与非独生子女结婚的规律。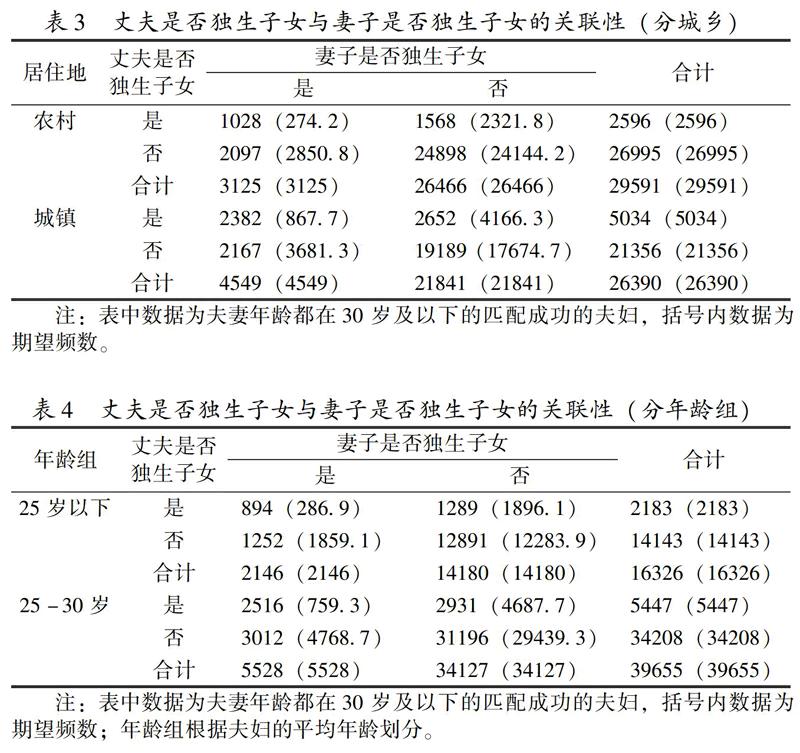

2. Logistic回归分析

上面的分析结果否定了“随机婚配”假定，而且无论从全国还是从分城乡、分年龄组的分析结果看，夫妇双方是否为独生子女的关联性是很强的。是什么原因导致独生子女更可能与独生子女结婚？

一些有关婚姻同质性匹配（homogamy）的研究认为，具有相同特征的人更可能结婚，其原因主要有两个：一是偏好（preference）问题，即人们在主观上更乐意选择与自己有相同特征的人组建家庭；二是机会（opportunity）问题，即一些结构性的因素限制了不同群体之间相互接触的机会，从而导致具有相同特征的人更可能结合在一起。

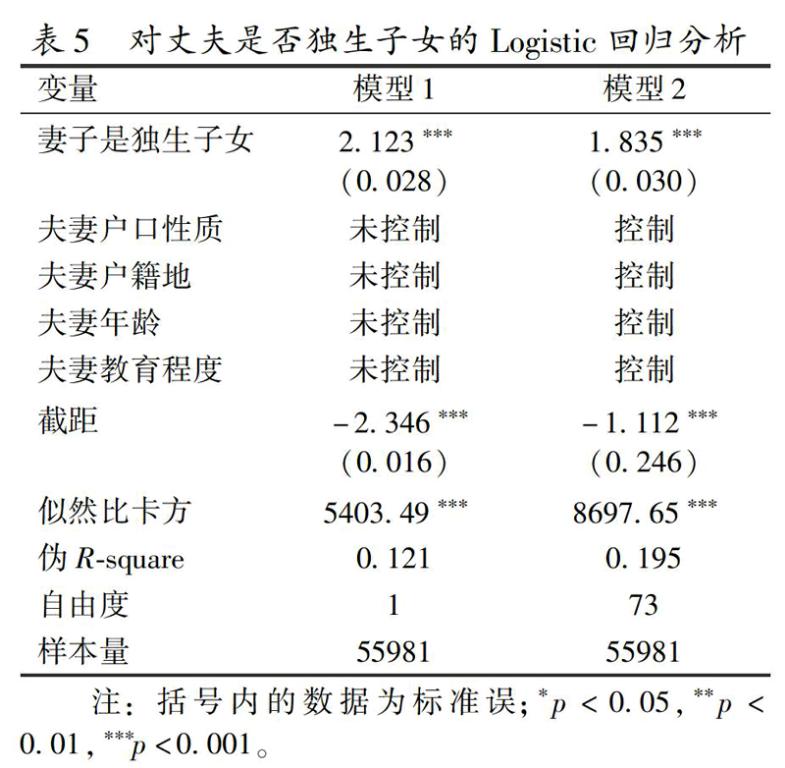
上述理论为我们研究独生子女之间的同质性婚配现象提供了很好的分析思路。一方面，从偏好的角度看，独生子女在成长经历、性格特征、生活方式等方面的相似性以及中国大多数省份允许“双独”夫妇生育二孩的政策规定都可能导致独生子女在择偶时更倾向于选择独生子女。另一方面，从机会的角度看，独生子女和非独生子女在城乡、地区、年龄和教育程度等方面的分布均存在显著差异，而中国人在择偶时总会对配偶的城乡属性、籍贯、年龄和教育程度进行严格筛选[8]，这种择偶过程中不可避免的选择性也会导致独生子女更可能与独生子女结婚。那么在中国，独生子女更可能与独生子女结婚的主要原因是什么？表5使用Logistic回归模型研究了这一问题。

表5采用了嵌套模型的分析策略。模型1仅纳入妻子是否为独生子女这一个自变量。结果显示，该变量对丈夫是否为独生子女具有非常显著的影响，其回归系数为2.123，换算成优势比后为8.35，这说明总体来看，夫妇双方在独生子女属性方面具有非常强的相关性。为了研究这种相关性的来源，我们又在模型1的基础上控制了夫妇双方的户口性质、户籍地、年龄和教育程度。从模型2可以发现，在控制住这四组变量之后，妻子是独生子女这个变量的统计检验结果依然非常显著，但是与模型1相比，该变量的回归系数下降到了1.835，降幅为13.6%。这种下降反映出，新加入的四组变量对独生子女之间的同质性婚配现象有一定程度的解释力。如前所述，人们总是倾向于同自己有相同城乡属性、来自同一地域范围、具有相似年龄和教育程度的人结婚，这就在很大程度上限制了择偶的范围。特别地，由于独生子女在城市、生育政策较严格的省份、低年龄组和高教育程度的人群中分布较为广泛，而非独生子女在农村、生育政策较宽松的省份、高年龄组和教育程度较低的人群中分布比较广泛，人们在择偶时对城乡、户籍地、年龄和教育程度的选择在无形中会降低独生子女与非独生子女结婚的机会，并增加了独生子女之间和非独生子女之间结婚的机会。所以，当我们控制住夫妇双方的这些特征之后，夫妇在独生属性上的关联性下降了。

但是从模型1到模型2，妻子是独生子女这个变量的回归系数仅下降了13.6%。这似乎意味着人们在上述四个维度上的选择性并不是导致独生子女更可能与独生子女结婚的主要原因。夫妇独生属性之间的相关主要表现为二者的净相关。换言之，这种相关性更可能来源于独生子女择偶时对独生子女本身的偏好。但事实果真如此吗？在回答这个问题之前，我们需要首先探讨两个方法上的问题。

3. Logistic回归系数的可比性

上述基于嵌套模型的分析建立在Logistic回归系数在不同模型之间可以相互比较这一前提之上。但遗憾的是，与线性回归模型不同，Logistic模型的回归系数并不直接可比[9-10]，其原因在于Logistic回归的误差项并不具有一个固定的可观测的测量尺度[11]。

我们可以用潜变量的方式来表示Logistic回归模型。定义一个连续潜变量y*

可以将y*理解为y=1的潜在倾向。，并规定当y*>0时，y=1；当y*≤0时，y=0。将y*表示为自变量

xk和误差项ε的一个线性函数，同时假定ε服从标准Logistic回归分布，可以证明公式（1）对y*所做的线性回归与公式（2）对取值为0和1的二分因变量y所做的Logistic回归是完全等价的。

由于未被解释的残差方差被设定成了固定值，只要被解释的方差有所增长，那么因变量y*的总方差也会有所增长。这意味着y*的总方差会随自变量数目的增多而增加（增加自变量通常会增加被解释的方差）。换言之，y*的测量尺度会随自变量的增多而增加。这导致在嵌套模型中，不同Logistic模型的回归系数是不可以直接比较的，因为全模型的回归系数总是要比简化模型来得大。

为了解决不同模型中Logistic回归系数的比较问题，温什普（Winship）和迈耶（Mare）建议，可以把不同模型的系数估计值都根据y*的标准差进行重新调整[12]。具体而言，就是用系数除以各自模型潜在因变量的估计标准差SD（y*），然后再进行比较[9]。SD（y*）的计算公式见公式（3）。这种方法也被称为“y*标准化”法。

在此之后，卡尔森（Karlson）等人又提出了一种被他们称为“KHB分解”的方法以解决嵌套模型中Logistic回归系数的比较问题[13]。该方法的核心是将纳入控制变量后Logistic回归系数的变化量分解为两个独立的部分，第一个部分叫做“混杂效应”，即增加控制变量对自变量系数的真实影响，这类似于一般线性回归模型中纳入控制变量后回归系数的变化；第二个部分叫做“标尺改变效应”，即增加控制变量后导致模型潜在因变量的测量尺度发生变化所造成的自变量系数的变化，这个部分是Logistic回归所特有的。由于篇幅限制，本文无法详细论述KHB方法的相关细节，有兴趣的读者可以参考卡尔森等人的论文[13]。

表6使用“y*标准化”法和“KHB分解”法重复了表5的分析过程。结果显示，在不纳入控制变量的情况下，SD（y*）的估计值为1.955；而在纳入控制变量后，由于被解释方差的增加，SD（y*）增加到了2.107。根据前面的分析，这会导致完全模型的回归系数出现一定程度的膨胀，进而导致低估回归系数从简化模型到完全模型的真实变化。计算结果显示，经过y*标准化以后，简化模型的回归系数为1.086，完全模型的回归系数为0.871，从简化模型到完全模型，系数真实下降的百分比为19.8%，高于直接比较时的13.6%。