Eventual Positivity of Hermitian Polynomials and Integral Operators

Colin TAN

1 Introduction

A central problem in real geometry is to establish certi ficates that directly witness the positivity of an algebraic morphism.The first of such certi ficates,known as positivstellensatze,was Artin’s 1927 solution to Hilbert’s 17th problem(see[1]).After a hiatus of four decades,Quillen[8]proved the first Hermitian postivstellensatz,thereby filling a gap in the literature.His positivestellensatz states that if a Hermitian bihomogeneous polynomial is strictly positive on the unit sphere,then repeated multiplication of the standard sesquilinear form to this polynomial eventually results in a sum of Hermitian squares.We will deduce this as Corollary 4.1 from the main result of this article.

Quillen’s positivstellensatz has attracted several proofs(see[3–5,7,10]).Some of these approaches lead to further improvements of Quillen’s result.For instance,Catlin-D’Angelo[4]gave a generalized embedding theorem of holomorphic vector bundles.To-Yeung’s positivstellensatz(see[10])is a more precise re finement of Quillen’s result.Putinar-Scheiderer[7]gave pesudoconvex boundaries other than the unit sphere on which every strictly positive algebraic morphism is a sum of Hermitian squares.

In 1997,Catlin-D’Angelo[3]independently rediscovered Quillen’s result.They observed that this positivstellensatz of Quillen is equivalent to the eventual positive-de finiteness of an associated integral operator.They then showed that this integral operator is well approximated by the Bergman kernel in the limit.Later,this approach was taken by Varolin[11].In this article,we give an elementary proof that follows Varolin’s approach and deduce Quillen’s positivstellensatz.

The global holomorphic sections of the tautological line bundleover a complex projective space form a complex vector spaceFix a basis(Φ0,···,Φn)ofLetThenrinduces a Hermitian metriconO(1)whose curvature is a Fubini-Study Kähler form on Pn.More generally,given a nonnegative integerd,a Hermitian metricponis globalizable if there exists a familyof complex constants doubly indexed by multi-indicesαandβof lengthdsuch that

whereCatlin-D’Angelo introduced this concept of gloablizability of the Hermitian metric in[4].

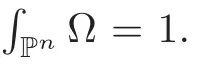
In this article,we show thatis eventually positive de finite.

Theorem 1.1Let d be a nonnegative integer and p be a Hermitian metric on If p is globalizable,then for m sufficiently large,the following asymptotic holds uniformly for

The author is aware that the above result(in fact,a stronger asymptotic without the(logm)n+2factor)would follow from pp.313–314 of[11],but is unable to follow the argument provided there.

In our proof,we show that the double integral(3.1)which represents this integral operator concentrates in a tubular neighborhood of the diagonal with radiusThis concentration result is inspired by the asymptotically concentration of the Bergman kernel along the diagonal.Our choice ofas a radius is in fluenced by Tian,who used the same radius to construct peak sections in[9]to prove the convergence of Bergman metrics.

2 Some Lemmas

We use the following notation and conventions throughout this article.Unless otherwise stated,asymptotics in this article are taken in an integermthat approaches in finity.Following Knuth[6],the Iverson bracket of a propositionτis the quantity

For example,the characteristic function of a subsetEof Pnis given byAnother example is the Kronecker delta,which is given byδij=[i=j].

Recall from the introduction thatfor some chosen basis(Φ0,···,Φn)ofH0(Pn,O(1)).This globalizable metricrcan be polarized to yield a metric on Pn.This metricis given by

For each pointxof Pn,there exists a canonical coordinatezcentered atxsuch that

For example,ifxis a point of Pn,then the subsetis biholomorphic to Cn.

Lemma 2.1Let p be a globalizable metric on O(d)→Pn.There exists a positive constant Cpsuch that

ProofFix a pointxof Pn.De fine a functionby

Choose a trivialization ofO(d).Choose a canonical coordinatezcentered atx.In this trivialization and coordinate,

Taking the holomorphic derivative,

Noting thatG(0)=1,evaluation atz=0 gives∂G(0)=0.The chain ruleimplies∂(G−1)(0)=0.Sincewe also have the vanishing of the antiholomophic derivatives,namely,

Ifthen

where

Hence we obtain the desired inequality by setting

LetVdenote the Lebesgue measure on Cn.Equip the unit sphereS2n−1of Cnwith its Haar measure,namely,the unique rotationally invariant Borel probability measure.The integral of a Borel measurable functioncan be transformed into polar coordinates(see p.6 in[2]):

Ifg:[0,∞)→C is Borel measurable,then(2.2)simpli fies to

ProofChoose a canonical coordinatezcentered atx.Recall that Ω is a normalization of the Fubini-Study volume form,so there exists a constantc＞0 such that

Hence

By the polar coordinate formula(2.3):

Combine(2.7)and(2.8)to obtain

Next we show(2.5).Note that

Hence

The inequalityholds for small∈＞0.By the assumptionhence

Hence(2.5)follows.

Finally we prove(2.6).In the canonical coordinatez,the volume form Ω has an upper bound

Lemma 2.3Letandare continuous functions,then

ProofFor convenience,we suppress the integrand of(2.9)in the notation.That is to say,when a single or double integral appears without the integrand,the reader understands that we refer respectively to the inner or double integral on the left-hand side of(2.9).

Suppose thatxis a point on Pn.By the Schwarz inequality,

Integrating with respect tox,

Apply the Schwarz inequality again,

By the Fubini theorem,we compute by using the Iverson bracket notation,

Hence by(2.10),

Corollary 2.1Under the same conditions as in the above lemma,the following inequality holds:

Lemma 2.4Let R0∈[0,∞]and let x be a point ofPn.If is a continuous function and f is holomorphic on,then

Choose a canonical coordinatezcentered atx.WriteB(R0)for the Euclidean ball in Cncentered at the origin of radiusR0.In terms of this coordinatez,

Transform this integral to polar coordinates using(2.2):

3 Proof of the Main Theorem

Letmbe a nonnegative integer andSuppose thatis a function withWe will choose a particularRlater.By our de finition(1.2)of

where

Term A will be dominant for our eventual choice ofR.

First we compute A.The zero section of the polarization ofplies offthe diagonal of Pn×Pn.Hence for sufficiently largem,we haveR(m)small,so that forthe expressionis well-de fined and holomorphic iny.Note that

Hence,we may use Lemma 2.4,which gives for eachx,

Integrating with respect tox,

Taking the difference of(2.4)and(2.5),

Hence

Next,we estimate B.By Lemma 2.1,The modulus of its integrand is

Hence

By Lemma 2.3,this becomes

Hence,by the asymptotics(2.4)and(2.6),

Finally,we estimate C.Let

By the compactness of Pn,this positive constantMpis finite.Hence

Hence

By Corollary 2.1,this becomes

Hence,by the asymptotic(2.5),

Sincecombining(3.2)–(3.4),

Indeed,such a function is given by

4 Application to Quillen’s Positivstellensatz

Letnbe a positive integer.Letdenote the complex polynomial algebra on the indeterminatesA multi-indexαis a sequence(α0,···,αn)ofn+1 nonnegative integers whose length|α|isα0+···+αn.Given a nonnegative integerd,a bihomogeneous polynomial of bidegree(d,d)is a finite sumwhere eachaαβis a complex scalar andThis polynomial is said to be Hermitian iffor eachαandβ.A polynomial is said to be holomorphic if only the indeterminatesZ0,···,Znoccur.Given a holomorphic polynomials(Z),write

With these concepts,we can state Quillen’s positivstellensatz.

Corollary 4.1Let p be a Hermitian bihomogeneous polynomial of bidegree(d,d).If＞0for each point ,then for sufficiently large m,there exists a basisof the holomorphic polynomials of degree m+d such that

ProofRecall from the introduction that we chose a basisofThe mapinduces a graded C-algebra isomorphism

This isomorphism induces the given Hermitian bihomogeneous polynomialpof bidegree(d,d)with a globalizable metric onO(d),which we will also denote aspby abuse of notation.

Recall the inner product onde fined by(1.1).Choose an orthonormal basisIn terms of this basis,writeSince this polynomialrmpis Hermitian,its coefficients form a Hermitian matrix(cδγ).Diagonalizing,there exists a unitary matrixP=(Pγη)and a real-valued diagonal matrixD=diag(···,λη,···)such thatIn particular,we haveHence,settingfη:=

We claim that(fη)is an orthonormal basis ofIndeed,the basis(eγ)is chosen to be orthonormal,so

By(1.1)and(1.2),the inner productis given by a double integral:

By(4.3)and the orthonormality of{fη},this becomes

By the main theorem,for sufficiently largemand eachfη,

A global section that forms part of a basis is necessarily nonzero,and henceThe above asymptotic has a leading coefficientformlarge.From(4.5),we getλη＞0.Thus(4.3)can be rewritten aswhereis a basis ofApply the C-algebra isomorphism(4.2)between C[Z]andto complete the proof.

AcknowledgementsThe author thanks his wife for her encouragement to complete this article.This article is a revision of part of the author’s PhD thesis.The author is grateful to his PhD supervisor Professor Wing-Keung To for his guidance.

[1]Artin,E.,Über die Zerlegung De finiter Funktionen in Quadrate,Abh.Math.Sem.Univ.,5(1),1927,100–115(in German).

[2]Axler,S.,Bourdon,P.and Ramey,W.,Harmonic Function Theory,2nd edition,Springer-Verlag,New York,2001.

[3]Catlin,D.W.and D’Angelo,J.P.,Positivity conditions for bihomogeneous polynomials,Math.Res.Lett.,4,1997,555–567.

[4]Catlin,D.W.and D’Angelo,J.P.,An isometric embedding theorem for holomorphic bundles,Math.Res.Lett.,6,1999,43–60.

[5]Drouot,A.and Zworski,M.,A quantitative version of Catlin-D’Angelo-Quillen theorem,Anal.Math.Phys.,3,2013,1–19.

[6]Knuth,D.E.,Two notes on notation,The American Mathematical Monthly,99(5),1992,403–422.

[7]Putinar,M.and Scheiderer,C.,Sums of Hermitian squares on pseudoconvex boundaries,Math.Res.Lett.,17(6),2010,1047–1053.

[8]Quillen,D.G.,On the representation of Hermitian forms as sums of squares,Inventiones Math.,5,1968,237–242.

[9]Tian,G.,On a set of polarized Kahler metrics on algebraic manifolds,J.Diff.Geom.,32,1990,99–130.

[10]To,W.K.and Yeung,S.K.,Effective isometric embeddings for certain holomorphic line bundles,J.London Math.Soc.,73(2),2006,607–624.

[11]Varolin,D.,Geometry of Hermitian algebraic functions.Quotients of squared norms,Amer.J.Math.,130,2008,291–315.