Existence and Global Asymptotic Behavior of Positive Solutions for Sublinear and Superlinear Fractional Boundary Value Problems∗

Imed BACHARHabibFaten TOUMI Zagharide ZINE EL ABIDINE

1 Introduction

Fractional differential equations have extensive applications in various fields of science and engineering.Many phenomena in viscoelasticity,electrochemistry,control theory,porous media,electromagnetism,and other fields,can be modeled by fractional differential equations.We refer the reader to[6–8,10–14,20–21,24–25,27–28,30–31]and the references therein for discussions of various applications.The existence,uniqueness and global asymptotic behavior of a positive continuous solution is an essential problem for fractional two-point boundary value problems.Such problems have been extensively investigated by many researchers,and various forms of the equation and boundary conditions have been discussed(see,for example,[1–2,4,9,11,15–16,18–19,23,26,32–34]and the references therein).In particular,in[2],Alsaedi studied the existence of a unique positive continuous solution to the following fourth order two-point value problem:

whereσ∈(−1,1)andpis a nonnegative continuous function satisfying some conditions related to the Karamata regular variation theory.Motivated by the above work,it is natural to ask when we can extend his result to the fractional setting.More precisely,in the first part of this paper,we are concerned with the following sublinear fractional differential two-point boundary value problem:

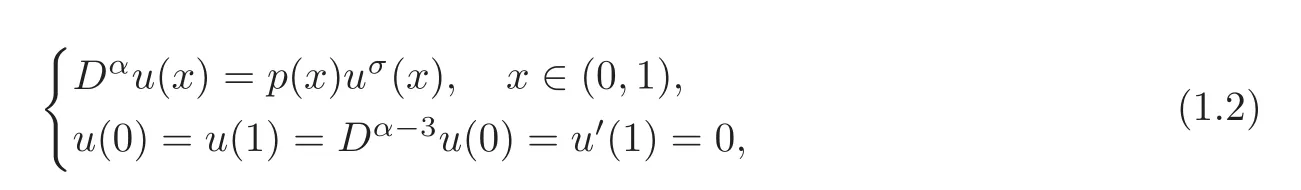
where 3＜α≤4,σ∈(−1,1)andpis a nonnegative continuous function on(0,1)that may be singular atx=0 orx=1 and satis fies some appropriate assumptions related to the Karamata classK(see De finition 1.1 below).Using the Schäuder fixed point theorem,we prove the existence of a unique positive continuous solution to problem(1.2).Further,by applying the Karamata regular variation theory,we establish sharp estimates on such a solution.To state our first existence result,we need some notations.We first introduce the Karamata classK.

De finition 1.1The class K is the set of Karamata functions L de fined on(0,η]by

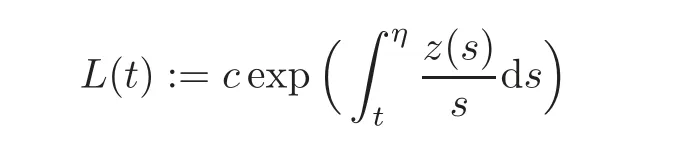
for some η＞1,where c＞0and z∈C([0,η])such that z(0)=0.

As a typical example of functions belonging to the classK,we quote

whereξjare real numbers,logjx=log◦log◦···logx(jtimes)andδis a sufficiently large positive real number such thatLis de fined and positive on(0,η]for someη＞1.For two nonnegative functionsfandgde fined on a setS,the notationmeans that there existsc＞0 such thatfor allx∈S.We denotex+=max(x,0)forx∈R and denote byB+((0,1))the set of all nonnegative measurable functions on(0,1).We denote byC((0,1))(resp.C([0,1]))the set of all continuous functions in(0,1)(resp.[0,1]).In the problem(1.2),we assume thatpis a nonnegative function on(0,1)satisfying the following condition:

(H)p∈C((0,1))such that

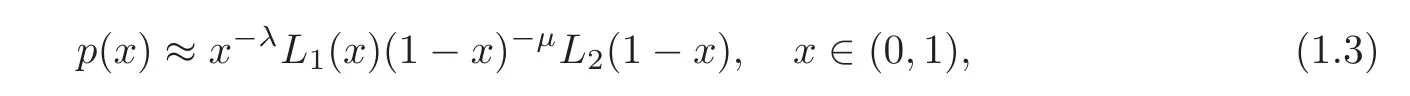
whereλ≤3+(α −3)σ,μ≤α −1+σandL1,L2∈Ksatisfying

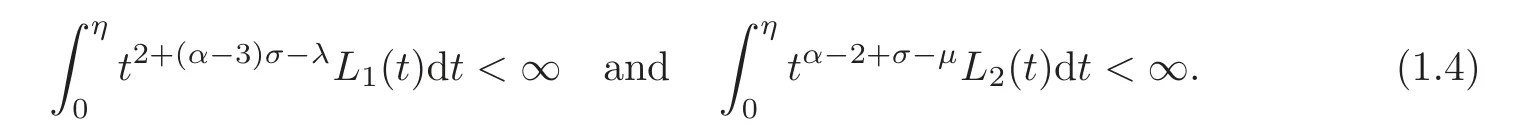
We de fine the functionθon[0,1]by

where

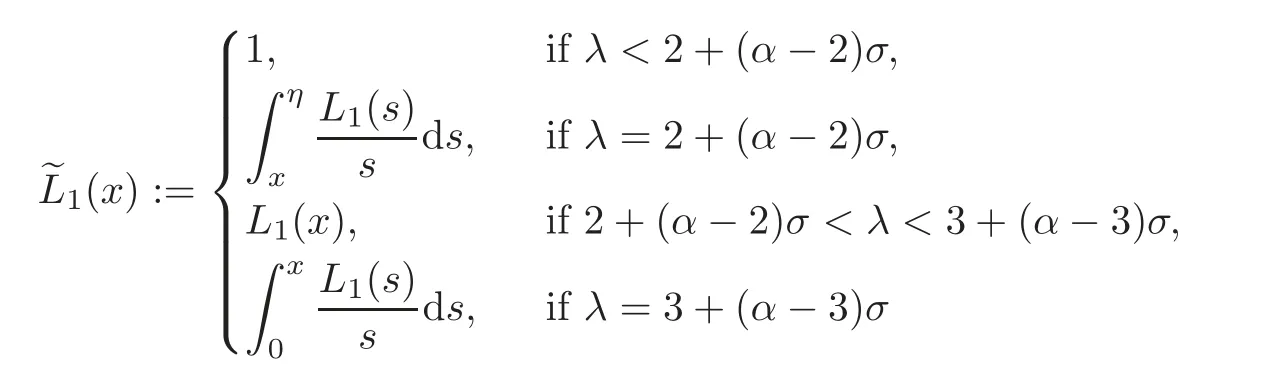
and

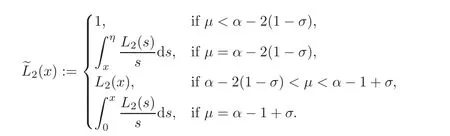
Our first existence result is the following.

Theorem 1.1Let σ∈(−1,1)and assume that p satis fies(H).Then problem(1.2)has a unique positive solution u∈C([0,1])satisfying for x∈[0,1],

This theorem extends the one obtained in[2]to the fractional setting.

In the second part of this paper,we are concerned with the following superlinear fractional boundary value problem:

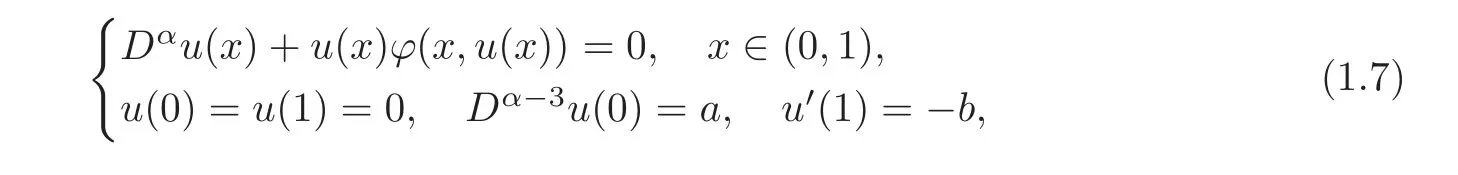
where 3＜α≤4,a,bare nonnegative constants such thata+b＞0 andϕ(x,t)is a nonnegative continuous function in(0,1)×[0,∞)that is required to satisfy some appropriate condition related to the following classKα.

De finition 1.2Let3＜α≤4.A Borel measurable function q in(0,1)belongs to the class Kαif q satis fies the following condition:

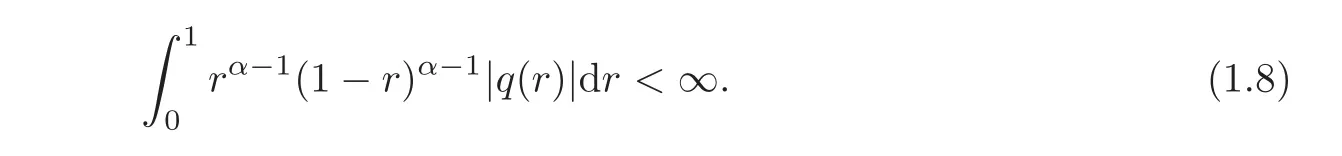
To state our second existence result,we introduce the following notations.We let

andbe the unique solution of the homogeneous problem

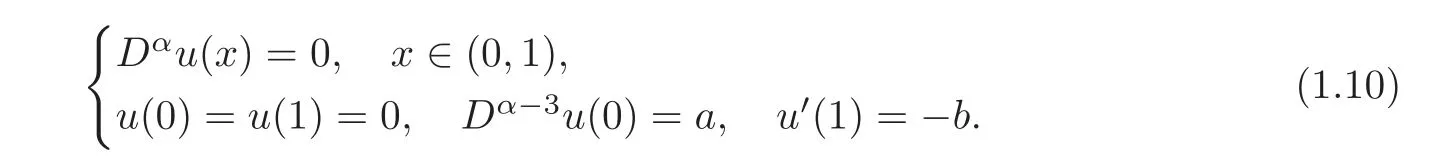
We denote byG(x,t)the Green’s function of the operatorwith boundary conditionsu(0)=u(1)=Dα−3u(0)=u′(1)=0,which can be explicitly given by(see Lemma 2.2)

For eachq∈Kα,we denote

and we will prove that ifq∈Kα,then

We require a combination of the following assumptions on the termϕ:

(H1)ϕis a nonnegative continuous function in(0,1)×[0,∞).

(H2)There exists a nonnegative functionwithsuch that for eachx∈(0,1),the mapis nondecreasing on[0,1].

(H3)For eachx∈(0,1),the functiont→tϕ(x,t)is nondecreasing on

We will first prove that ifqis a nonnegative function inwithandψis a positive measurable function,then the following problem

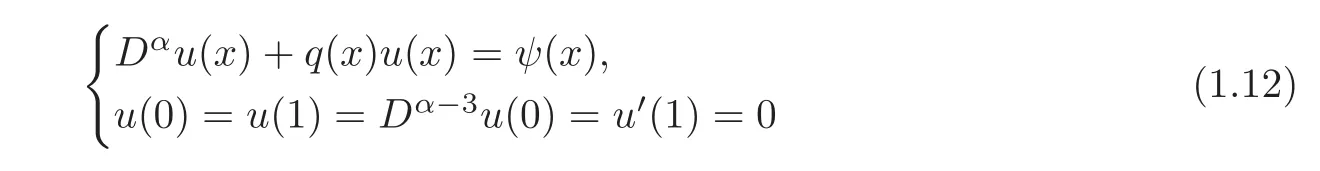
has a positive solution.It turns out to prove that problem(1.12)admits a positive Green’s functionG(x,t).Based on the construction of this Green’s function and by using a perturbation argument,we prove the following theorem.

Theorem 1.2Assume(H1)–(H2),and then problem(1.7)has a positive solution u in C([0,1])satisfying

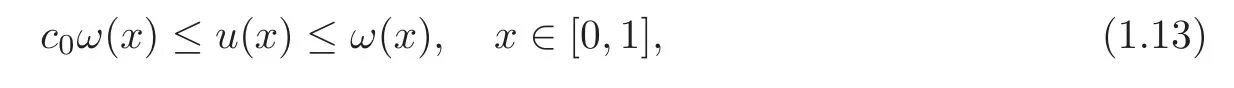
where c0is a constant in(0,1).Moreover,if hypothesis(H3)is also satis fied,then the solution u to problem(1.7)satisfying(1.13)is unique.

Corollary 1.1Let f be a nonnegative function in C1([0,∞))such that the maptf(t)is nondecreasing on[0,∞).Let p be a nonnegative continuous function on(0,1)such thatthe functionbelongs to the class Kα.Then forthe following problem

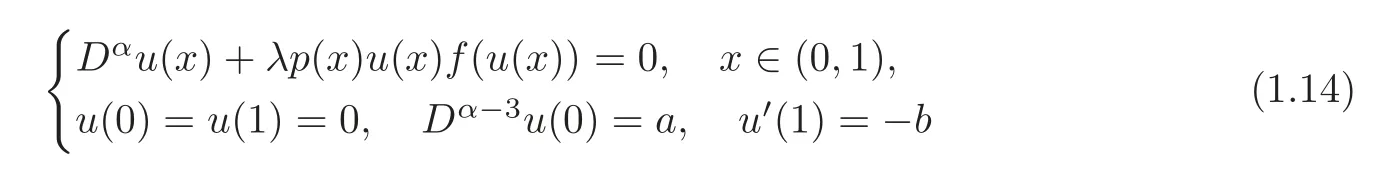
has a unique positive solution u in C([0,1])satisfying

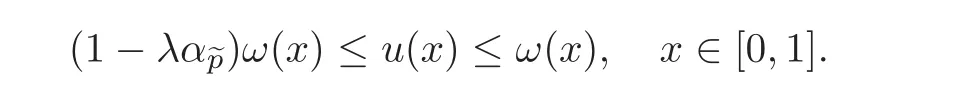
These results extend the ones obtained in[3]withα=4 to the fractional setting.Also observe that in Theorem 1.2,we obtain a positive solutionuinC([0,1])to problem(1.7),whose behavior is not affected by the perturbed term.That is,it behaves like the solutionωof the homogeneous problem(1.10).As a typical example of nonlinearity satisfying(H1)–(H3),we quote,forσ≥0,pbeing a positive continuous function on(0,1)such that and

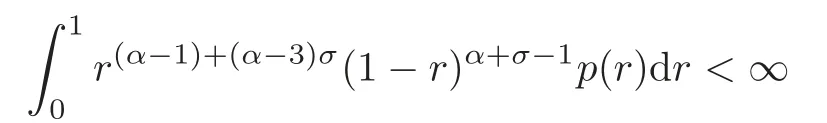
The rest of this paper is organized as follows.In Section 2,we prove some sharp estimates on the Green’s functionG(x,t),including the following inequality:For eachx,r,t∈(0,1),

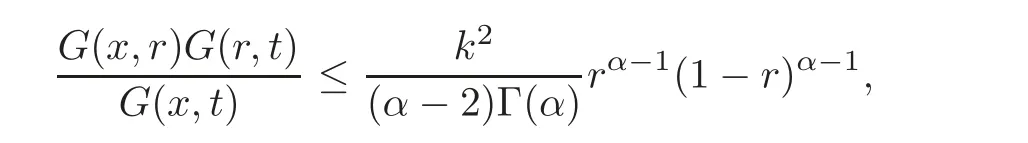
wherek:=max((α−2)2,α−1).In particular,we deduce from this inequality that for eachq∈Kα,αq＜∞.In Section 3,we present some known results on functions belonging to the classKand we establish sharp estimates on some potential functions.Exploiting theses results,we prove Theorem 1.1 by means of the Schäuder fixed point theorem.In Section 4,for a given functionq∈Kαwithwe construct the Green’s functionG(x,t)of the boundary value problem(1.12).Next,we establish some estimates on this function.In particular,we prove that forwe have

Also we prove the following resolvent equation:

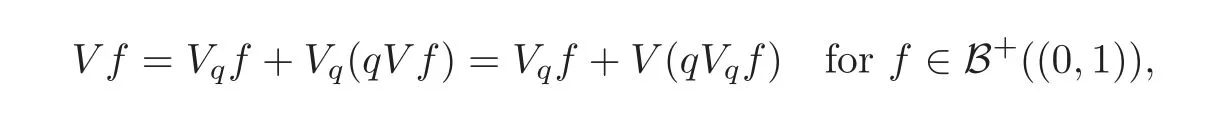
where the kernelsVandVqare de fined onB+((0,1))by

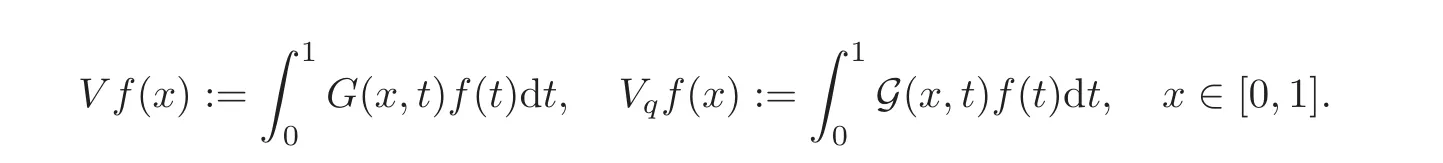
By using the above results and a perturbation argument,we prove Theorem 1.2.Finally,we give some examples to illustrate our existence results.

2 Fractional Calculus and Estimates on the Green’s Function

2.1 Fractional calculus

For the convenience of the reader,we recall in this section some basic de finitions of fractional calculus(see[12,25,27]).

De finition 2.1The Riemann-Liouville fractional integral of order β＞0for a measurable function f:(0,∞)→Ris de fined as

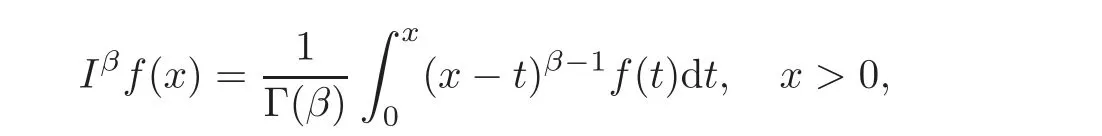
provided that the right-hand side is pointwise de fined on(0,∞).HereΓis the Euler Gamma function.

De finition 2.2The Riemann-Liouville fractional derivative of order β＞0for a measurable function f:(0,∞)→Ris de fined as

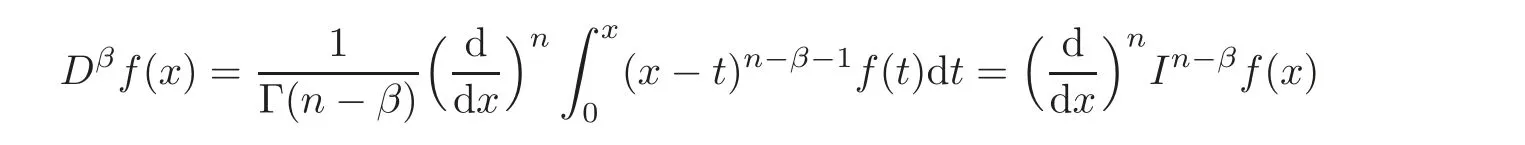
provided that the right-hand side is pointwise de fined on(0,∞).Here n=[β]+1and[β]denotes the integer part of the number β.

Lemma 2.1Let β＞0and u∈C((0,1))∩L1((0,1)).Then we have the following assertions:

(i)For0＜γ＜β, and

(ii)Dβu(x)=0if and only ifwhere m is the smallest integer greater than or equal to β.

(iii)Assume that Dβu∈C((0,1))∩L1((0,1)),and then

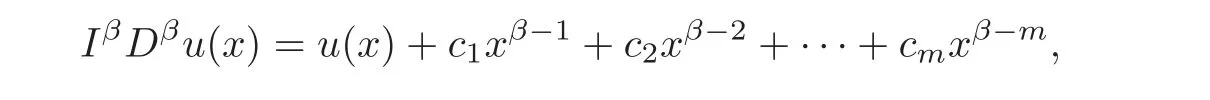
ci∈R,i=1,···,m,where m is the smallest integer greater than or equal to β.

2.2 Estimates on the Green’s Function

In this section,we derive the corresponding Green’s function for the homogeneous boundary value problem(1.2)and we prove some estimates on this function.

Lemma 2.2Let3＜α≤4and f∈C([0,1]),and then the boundary-value problem

has a unique solution

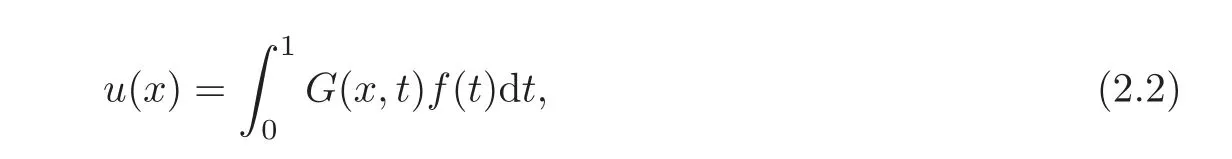
where for x,t∈[0,1],

is the Green’s function of boundary-value problem(2.1).

ProofBy means of Lemma 2.1,we can reduce equationDαu(x)=f(x)to an equivalent integral equation

where(c1,c2,c3,c4)∈R4.The boundary conditionu(0)=0 implies thatc4=0.Applying the operatorDα−3to both sides of(2.4)and using Lemma 2.1(i),we obtain that

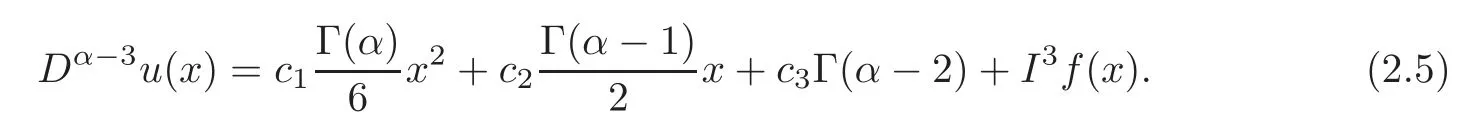
The boundary conditionDα−3u(0)=0 givesc3=0.Hence

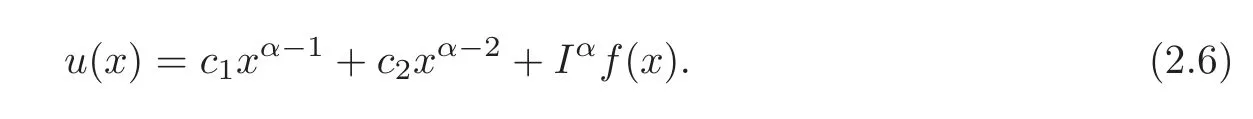
Now,using(2.6)and the boundary conditionsu(1)=u′(1)=0,we obtain

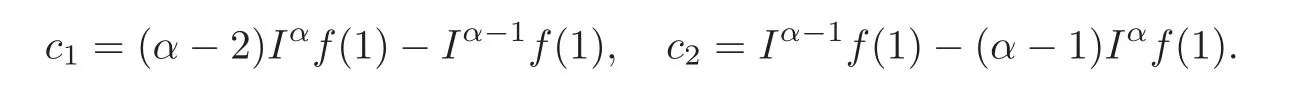
Therefore the unique solution of problem(2.1)is

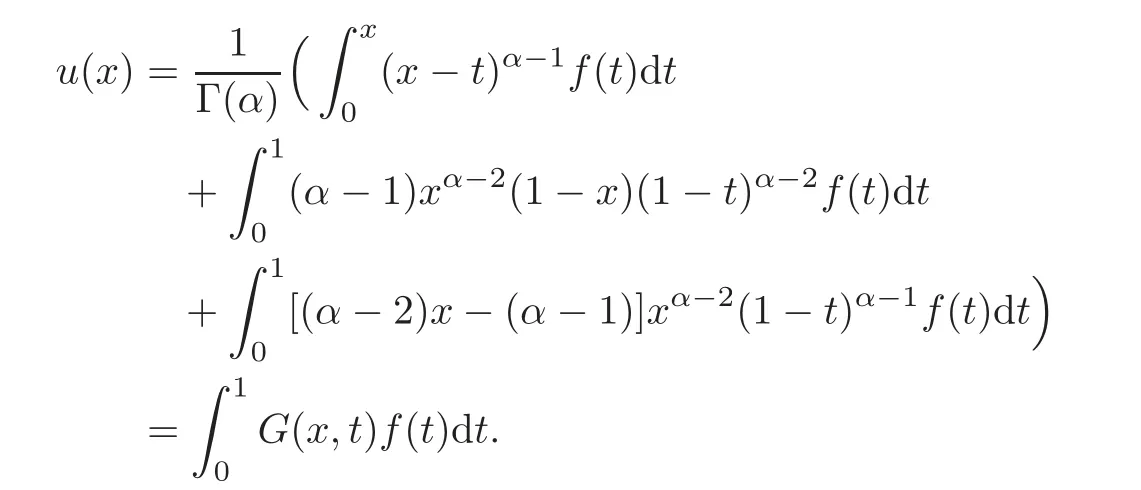
Proposition 2.1Let3＜α≤4and k=max((α−2)2,α−1).The Green’s function G(x,t)satis fies the following properties on[0,1]×[0,1]:

(i)(α−2)H(x,t)≤Γ(α)G(x,t)≤kH(x,t),where

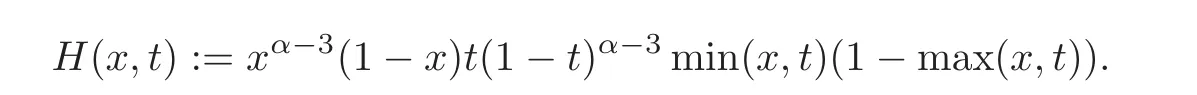
(ii)(α−2)xα−2(1−x)2t2(1−t)α−2≤Γ(α)G(x,t)≤kxα−3(1−x)t2(1−t)α−2.

(iii)G(x,t)=G(1−t,1−x).

Proof(i)We divide the proof into two cases.

Case 10≤t≤x≤1.First,we remark that

This implies that

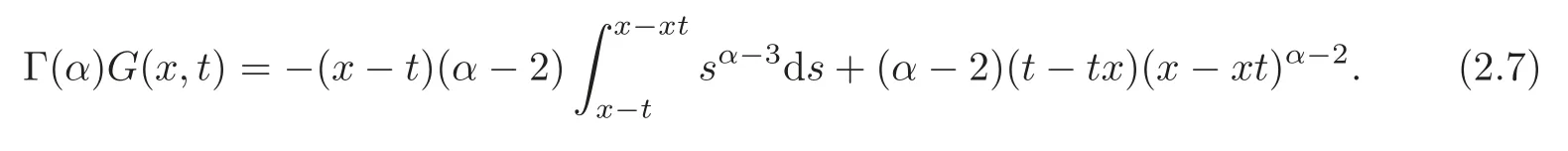
So,we get

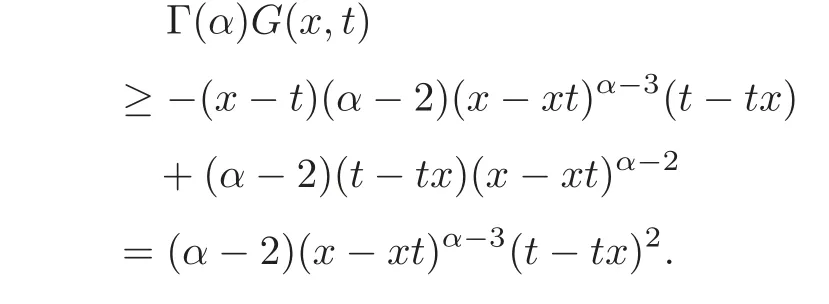
That is

On the other hand,using(2.7),we obtain

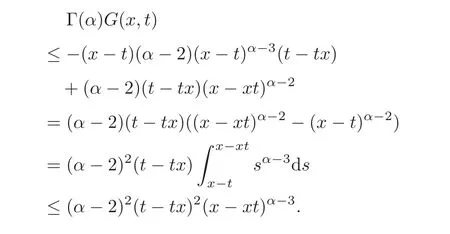
That is

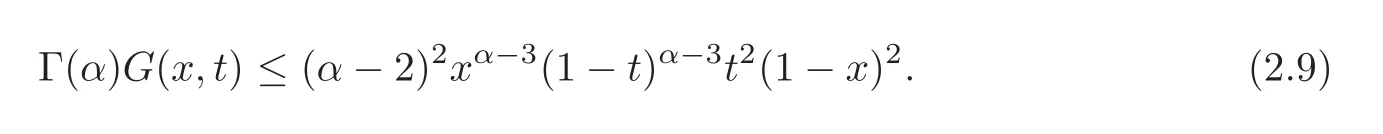
Combining(2.8)and(2.9),we get,for 0≤t≤x≤1,

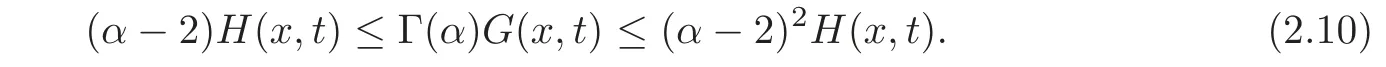
Case 20≤x≤t≤1.We have

Sincet−x≥0,we get

Moreover,using(2.11)and the fact thatt−x≤t(1−x),we obtain that

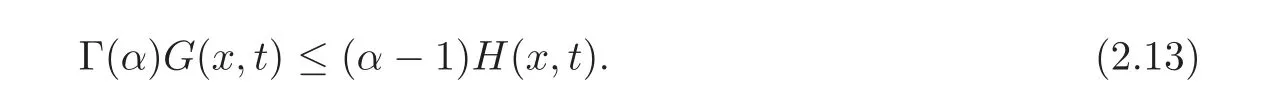
From(2.12)and(2.13),we have,for 0≤x≤t≤1,

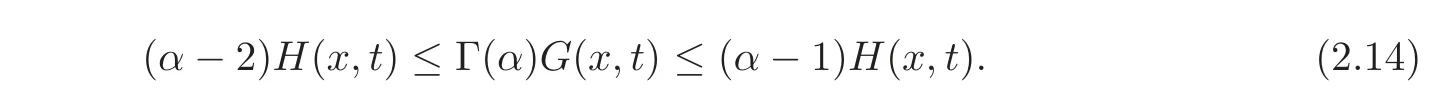
The assertion(i)holds immediately from(2.10)and(2.14).

(ii)The assertion follows from(i)and the fact that forx,t∈[0,1],we have

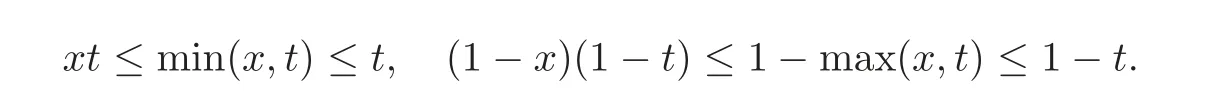
(iii)The assertion follows from(2.3)and a simple computation.

Remark 2.1Note that estimates on the Green’s functionG(x,t)obtained in the previous proposition improve those obtained in[32,Lemma 2.4].

As an immediately consequence of the assertion(ii)of Proposition 2.1,we obtain the following.

Corollary 2.1Let f∈B+((0,1)),and then the functionis continuous on[0,1]if and only if the integraldt converges.

Proposition 2.2Let3＜α＜4and f be a function such that the mapis continuous and integrable on(0,1).Then V f is the unique solution in C([0,1])of the boundary value problem

ProofFrom Corollary 2.1,the functionV fis inC([0,1]).This implies thatis bounded on[0,1].So by using Fubini’s theorem,we obtain

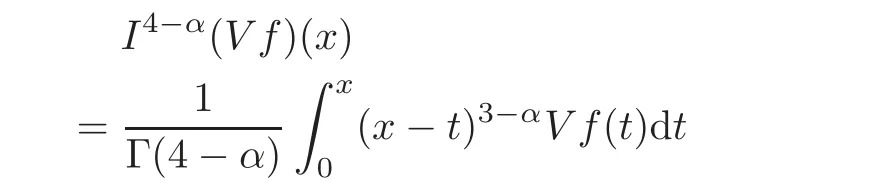
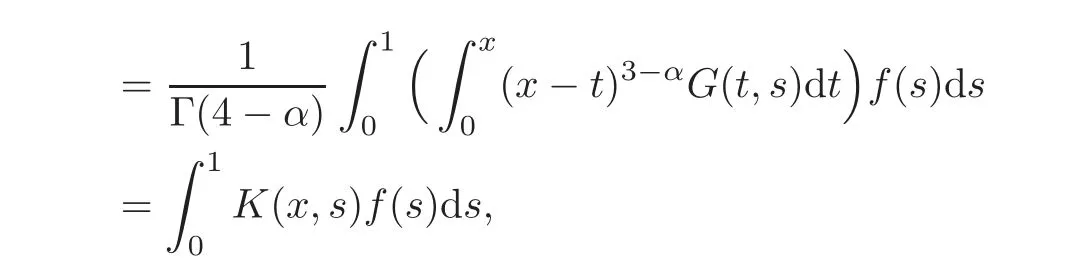
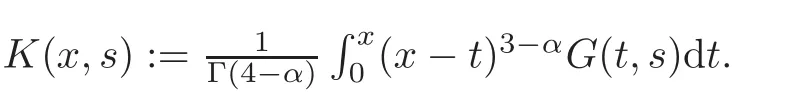
Next,we aim at giving an explicit expression of the kernelK(x,s).To this end,observe that by making the substitutiont=s+(x−s)θ,we obtain,forγ,ν＞−1,

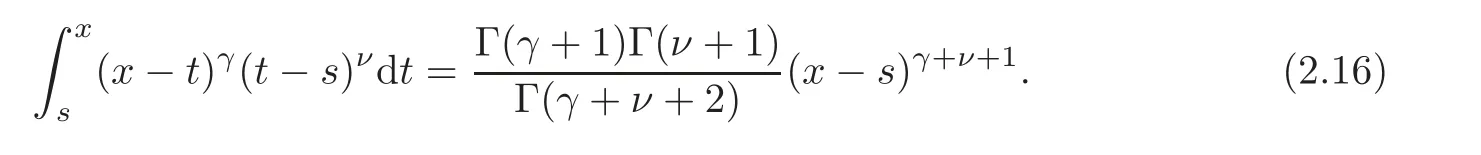
Using this fact and(2.3),we deduce that

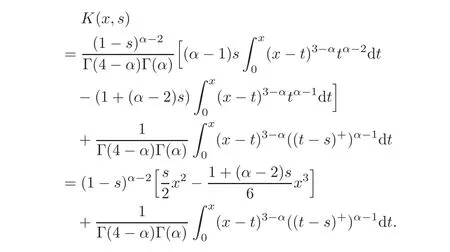
Now,assume thats≤x,and then by(2.16)we have

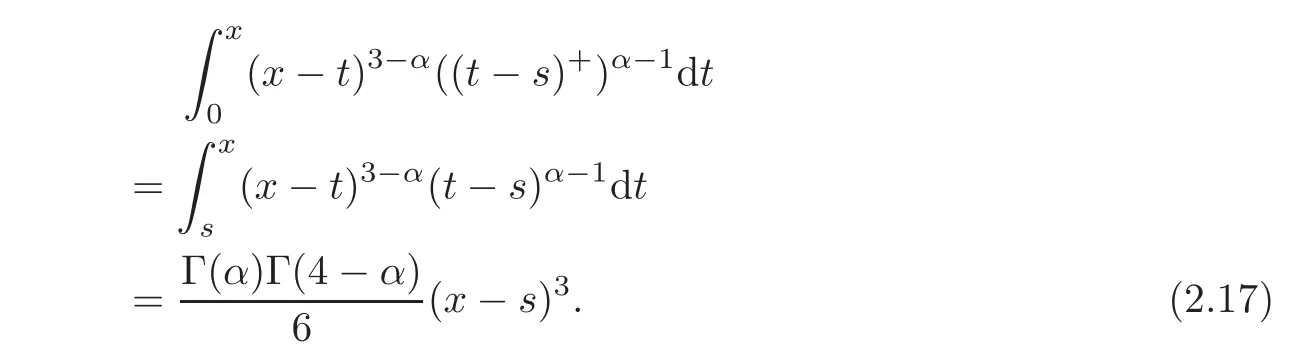
On the other hand,if 0≤t≤x≤s,we have

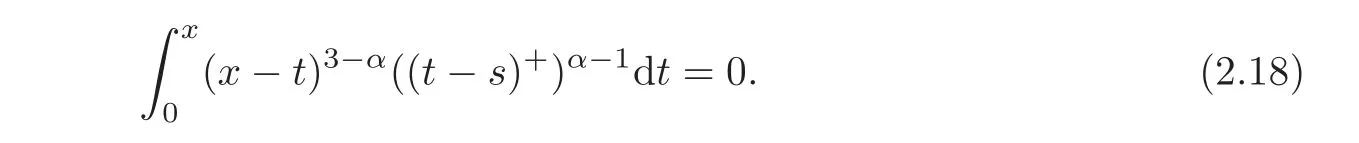
So,combining(2.17)and(2.18),we obtain

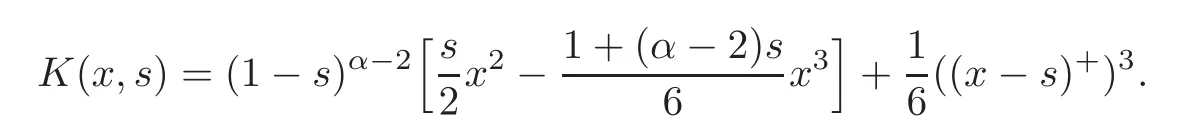
Hence forx∈[0,1],we have

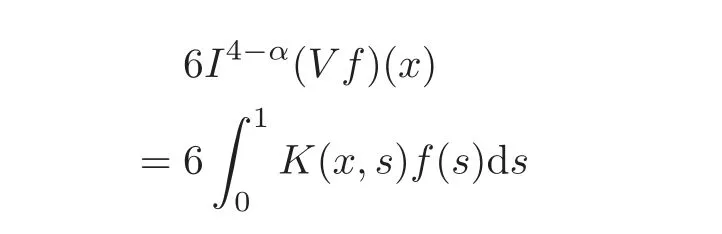
We claim that

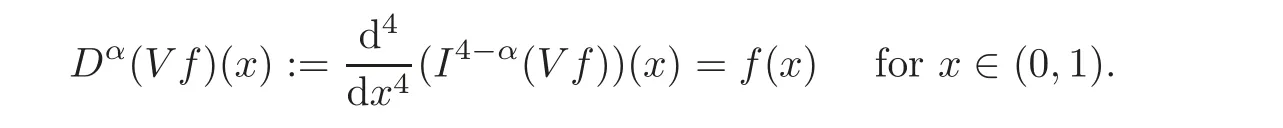
Indeed, firstly note that from the hypothesis,the functionis continuous and integrable near 0 and the functionis continuous and integrable near 1.This implies in particular that J5(x)and J6(x)are differentiable on(0,1).On the other hand,since

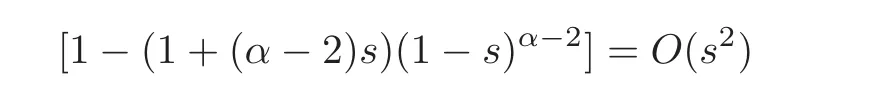
andnear 0,it follows thatand J4(x)are differentiable on(0,1).

So,by simple computation,we obtain

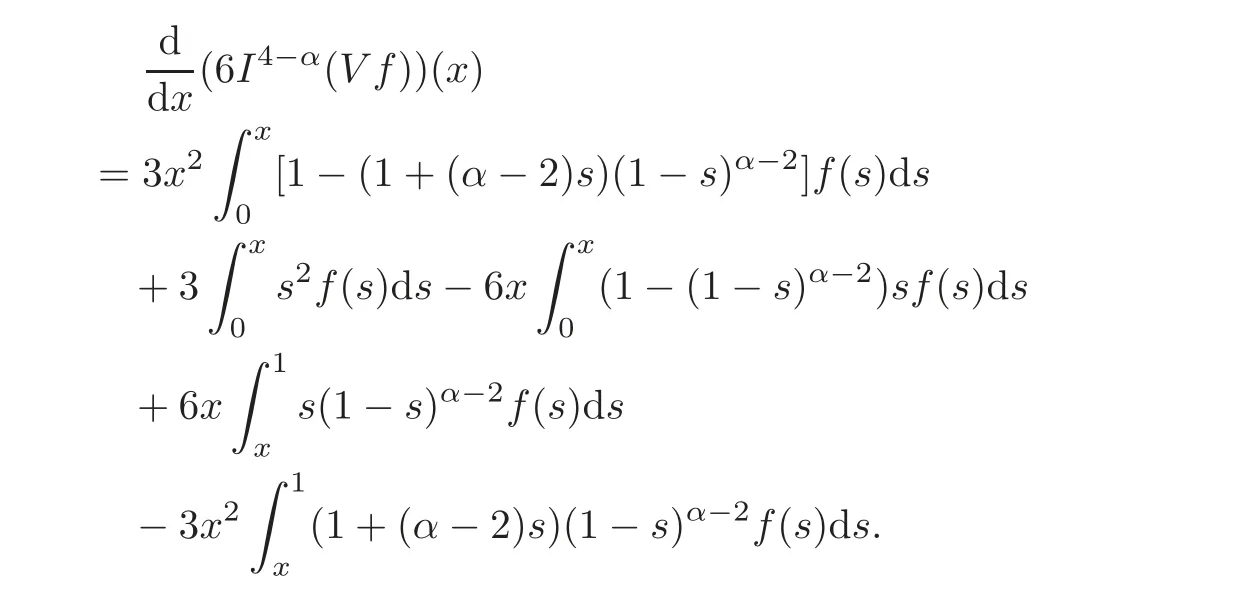
By similar arguments as above,we obtain

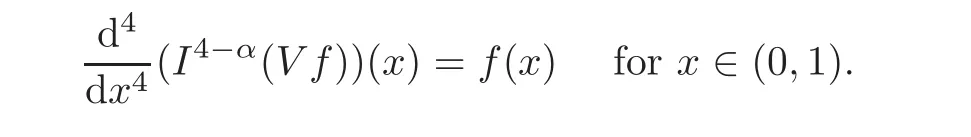
Next,we need to verify that the functionV fsatis fies the boundary conditions.By Proposition 2.1(ii),there exists a nonnegative constantcsuch that

So,it follows thatV f(0)=V f(1)=0.On the other hand,by Proposition 2.1(i),for eacht∈[0,1],we have

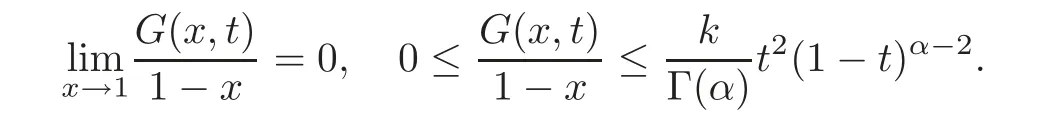
This implies by the dominated convergence theorem thatIt remains to prove

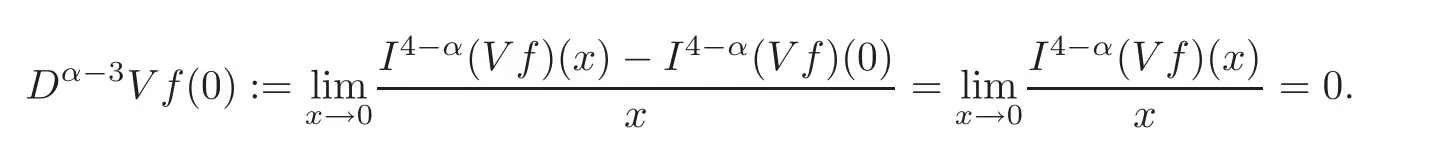
To this end,we only need to verify that

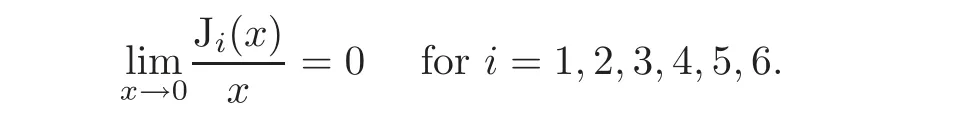
The assertion is clear for J1(x),J3(x)and J4(x).

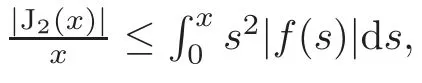
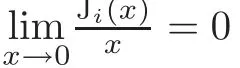
Remark 2.2Note that the conclusion of Proposition 2.2 is also valid forα=4(see[2]).

Proposition 2.3We have,for each x,r,t∈(0,1),

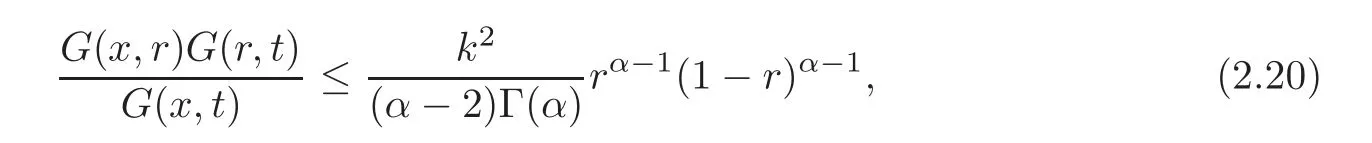
where k=max((α−2)2,α−1).

ProofUsing Proposition 2.1(i),we have,for eachx,r,t∈(0,1),

We claim that

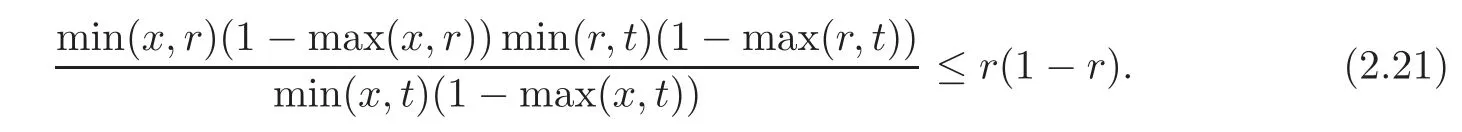
Indeed,by symmetry,we may assume thatx≤t.Then we deduce that

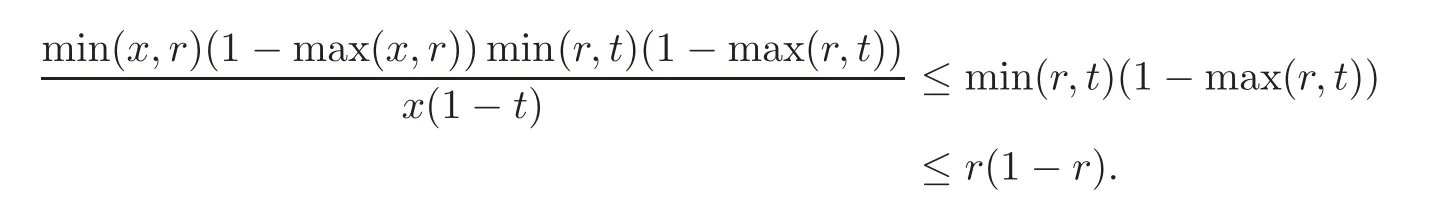
Now,by using(2.21),we obtain the required result.

Next we recall thatwhere

andh2(x)=xα−2(1−x)forx∈[0,1].

Proposition 2.4Let q be a function in Kα,and then we have that

(i)

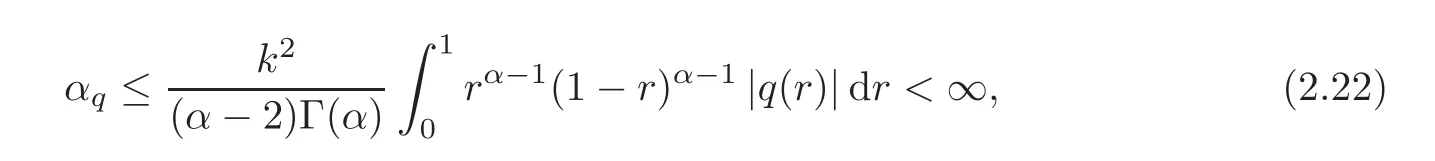
where k=max((α−2)2,α−1)and αqis given by(1.11);

(ii)for x∈[0,1],

(iii)for x∈[0,1],

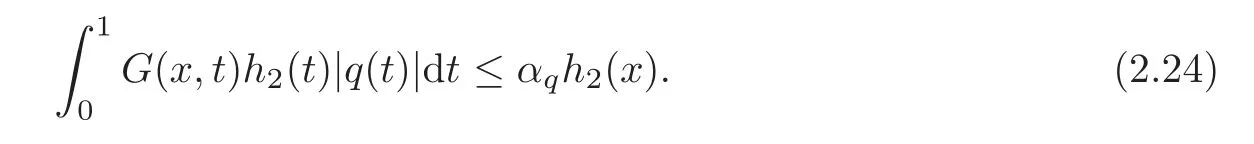
In particular for x∈[0,1],

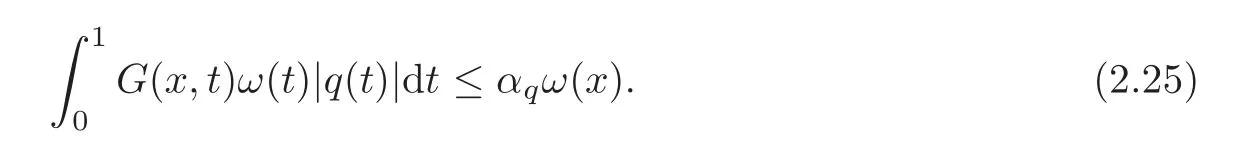
ProofLetqbe a function inKα.

(i)The inequality(2.22)follows from(1.11)and(2.20).

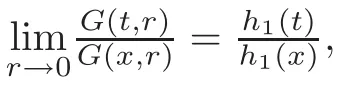
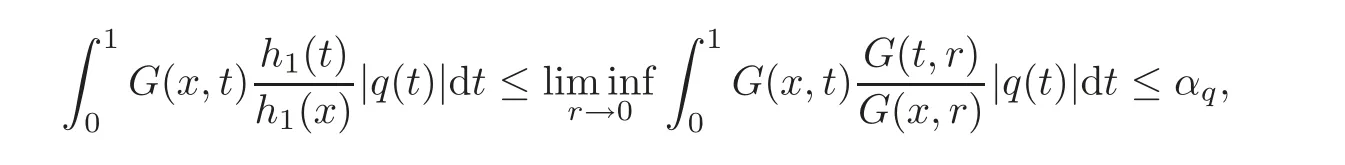
which implies that forx∈[0,1],

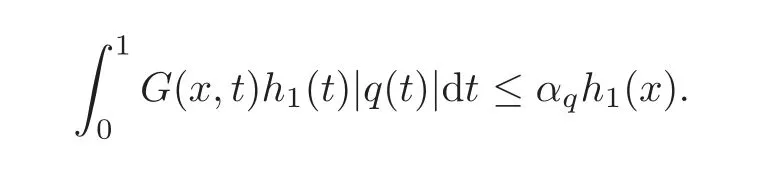
(iii)Similarly,we prove inequality(2.24)by observing that

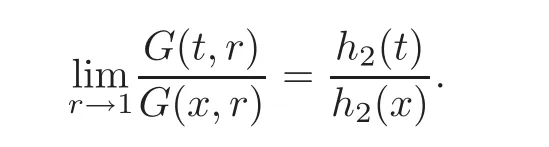
Inequality(2.25)follows from(2.23)–(2.24)and the fact that.

3 First Existence Result

In this section,we aim at proving Theorem 1.1.

3.1 Karamata class and sharp estimates on some potential functions

In this subsection,we recall some fundamental properties of functions belonging to the classKand we establish estimates on some potential functions.

Lemma 3.1(see[22,29])Let γ∈Rand L be a function in K de fined on(0,η].Then we have that

Lemma 3.2(see[5,29])(i)Let L∈K and∈＞0.So then we have

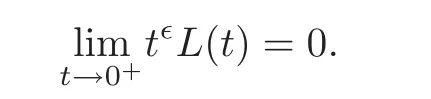
(ii)Let L1and L2∈K de fined on(0,η]and p∈R.Then functions

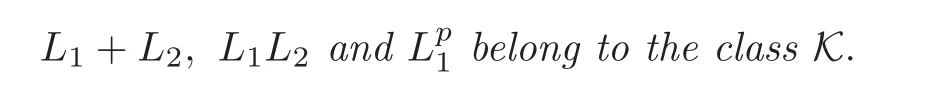
(iii)Let L∈K de fined on(0,η].So then we have

In particular,

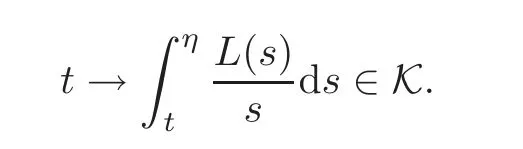
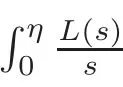
In particular,

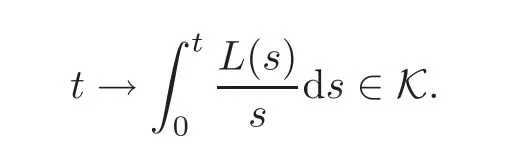
Next,we shall prove sharp estimates on the potential functionV(pθσ),wherepis a function satisfying(H)andθis the function given by(1.5).

To this end,we need the following proposition.

Proposition 3.1Let γ≤3,ν≤α−1and L3,L4∈K such that

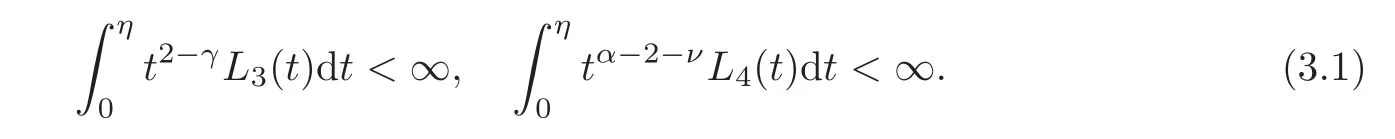
Put

Then we have,for x∈[0,1],

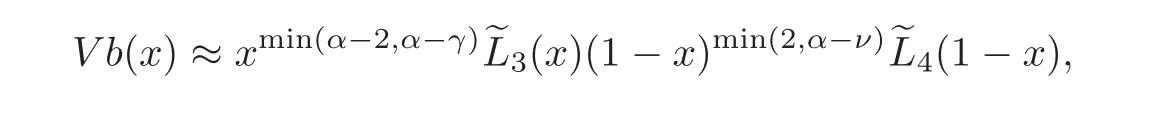
where

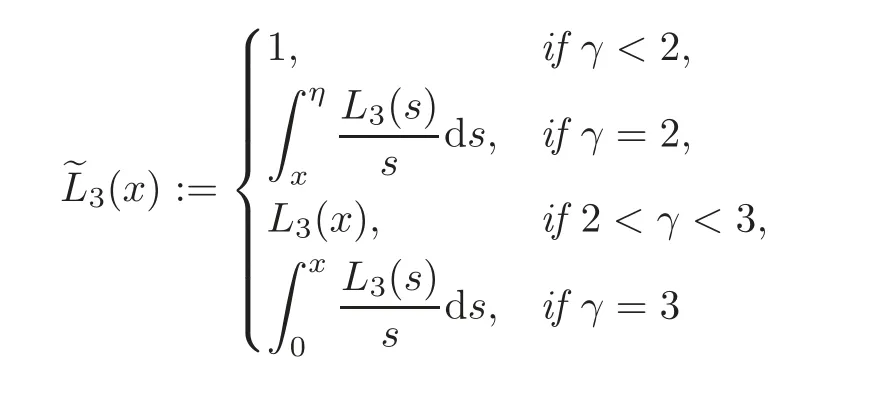
and

ProofForx∈[0,1],we have

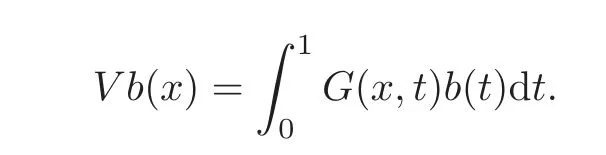
Using Proposition 2.1(i),we obtain that

In what follows,we distinguish two cases.

Case 1.In this case,we haveSo,we obtain

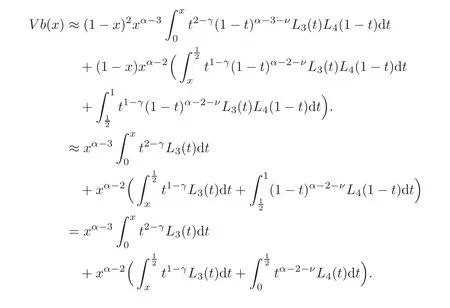
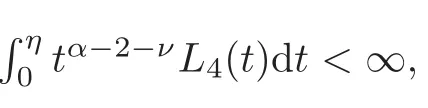
Using Lemma 3.1 and hypothesis(3.1),we deduce that

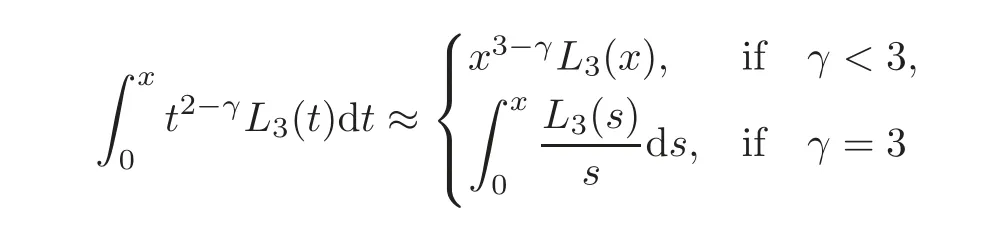
and

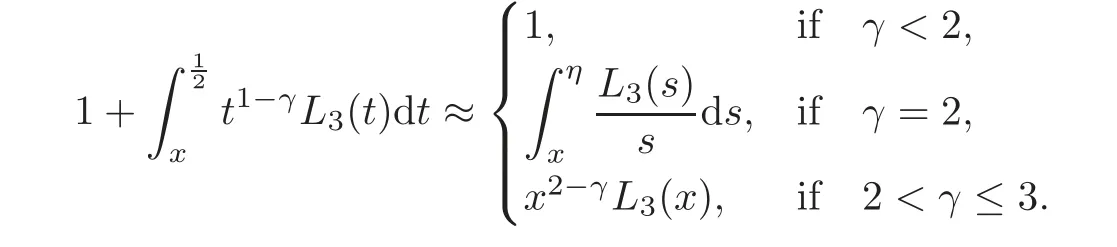
Hence,it follows by Lemmas 3.1–3.2 and hypothesis(3.1)that for

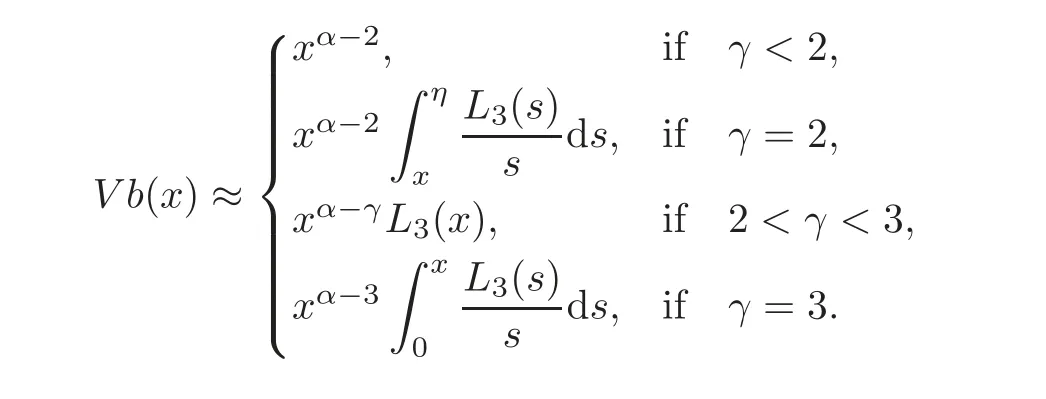
That is

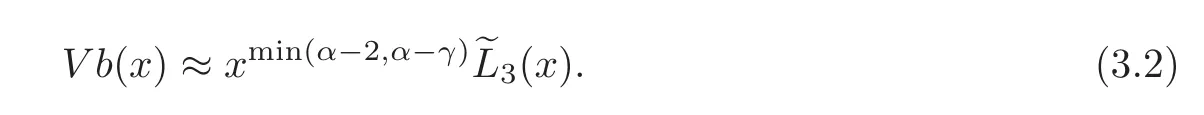
Case 2.In this case,we haveTherefore,we obtain

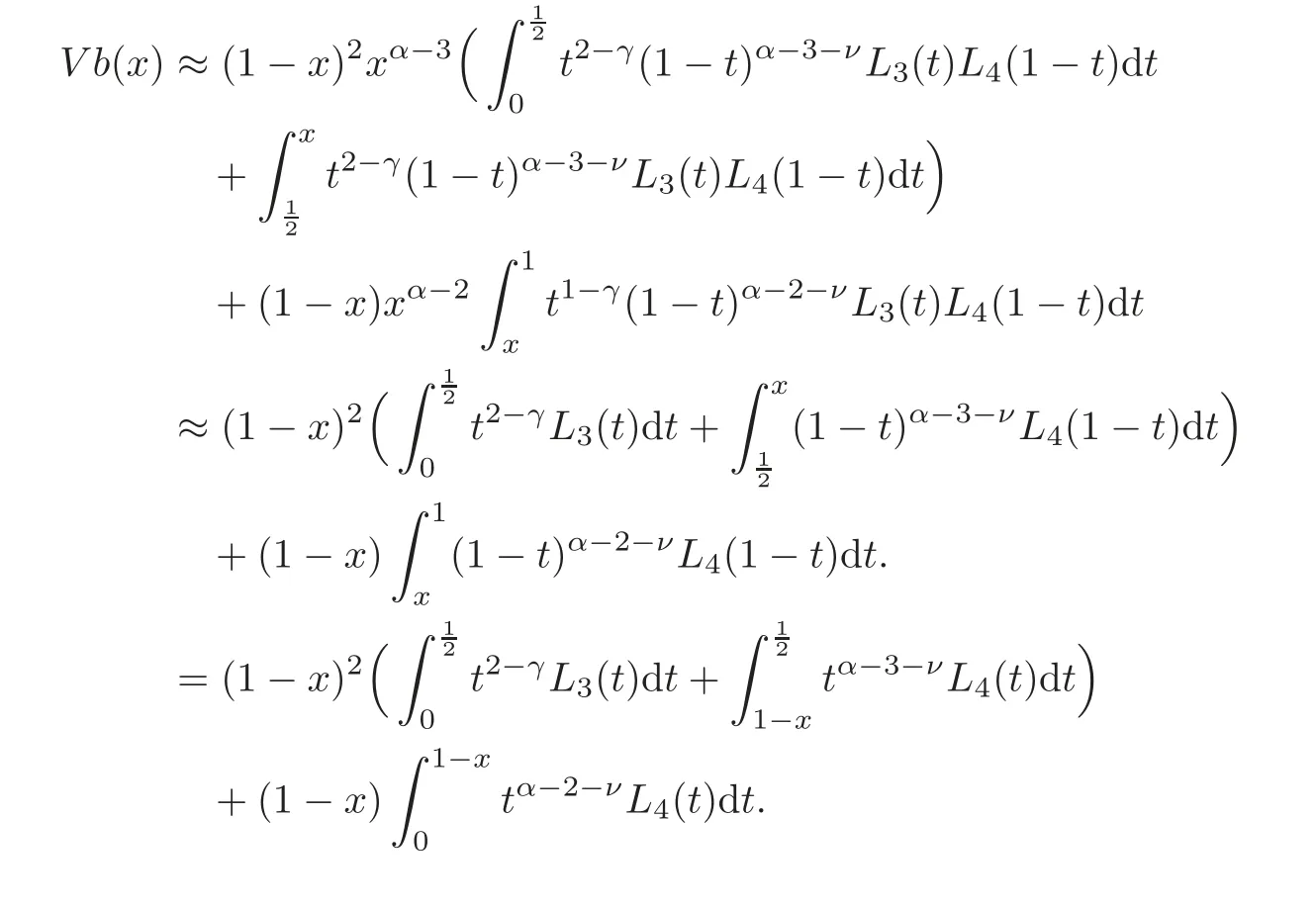
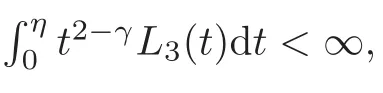
Using again Lemma 3.1 and hypothesis(3.1),we deduce that

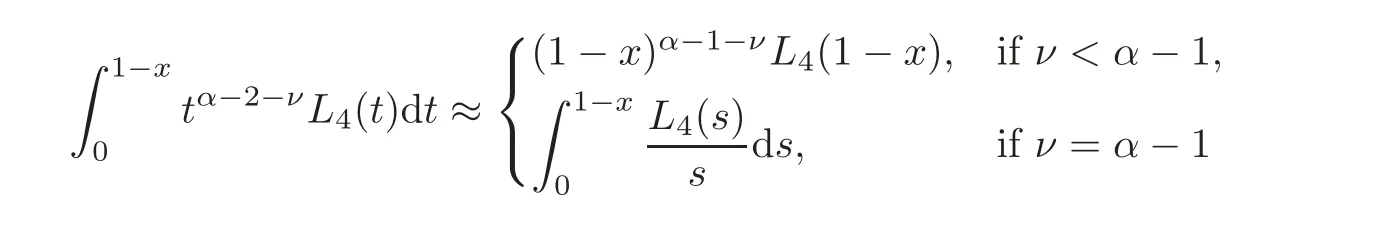
and

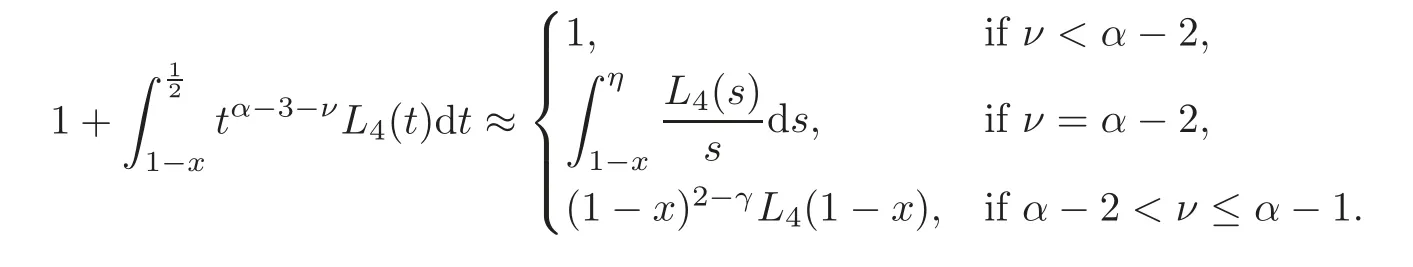
Hence,it follows by Lemmas 3.1–3.2 and hypothesis(3.1)that for

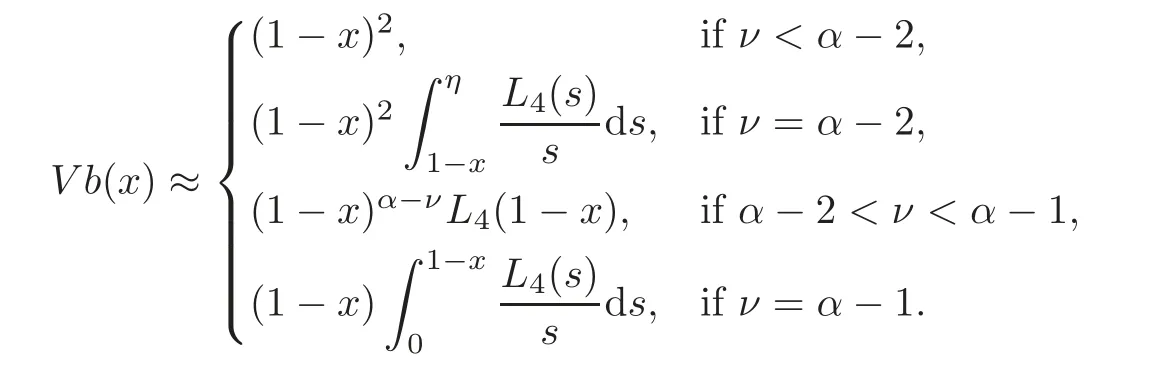
That is

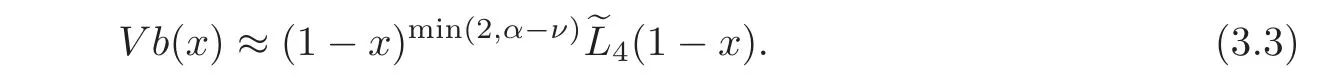
This together with(3.2)implies that forx∈[0,1],we have

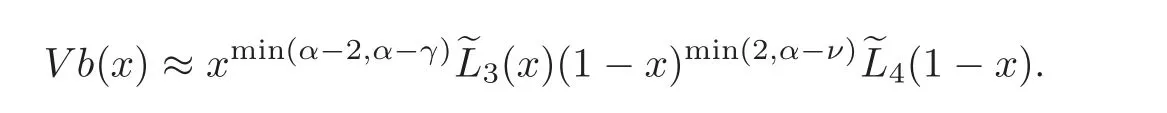
This ends the proof.

The following proposition plays a crucial role in the proof of Theorem 1.1.

Proposition 3.2Let p be a function satisfying(H).Then we have,for x∈[0,1],

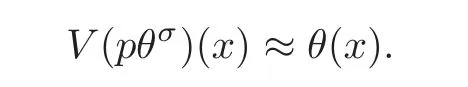
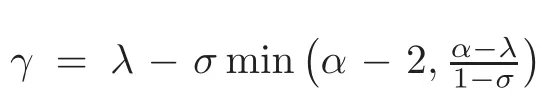
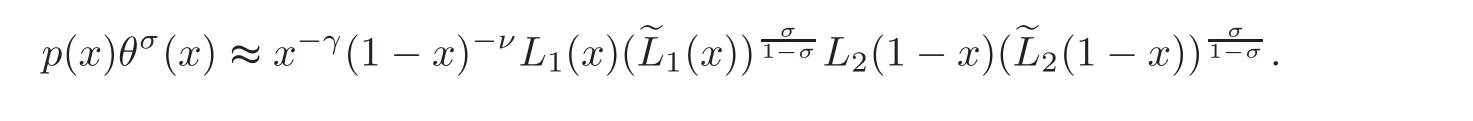
So,using Lemmas 3.1–3.2 and Proposition 3.1 withandwe deduce that for eachx∈[0,1],

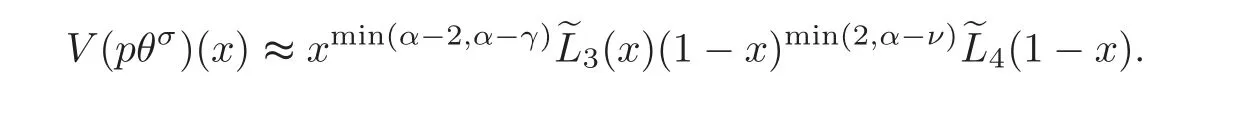
Since

we conclude by elementary calculus that forx∈[0,1],

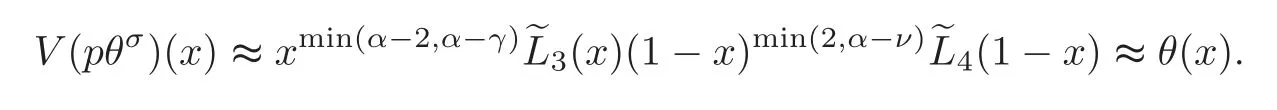
This completes the proof.

3.2 Proof of Theorem 1.1

Letpbe a function satisfying(H)and letθbe the function given by(1.5).By Proposition 3.2,there existsM≥1 such that for eachx∈[0,1],

We shall use a fixed point argument to construct a solution to problem(1.2).For this end,putand consider the closed convex set given by

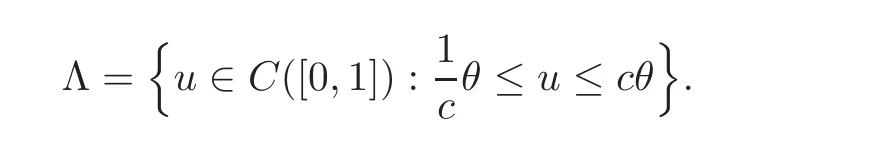
Obviously,the functionθbelongs toC([0,1])and so Λ is not empty.We de fine the operatorTon Λ by

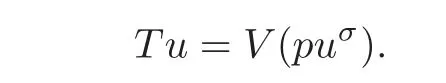
For this choice ofc,we can easily get that foru∈Λ,we haveNow,since the functionis continuous on[0,1]×[0,1]and the functionis integrable on(0,1),we deduce that the operatorTis compact from Λ to itself.So,by the Schäuder fixed-point theorem,there exists a functionu∈Λ such that

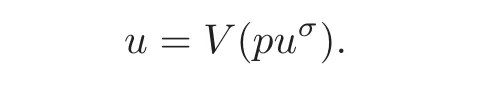
It remains to prove thatuis a positive continuous solution of problem(1.2).Indeed,sinceis continuous and integrable on(0,1),then it follows from Proposition 2.2 that the functionuis a positive continuous solution of problem(1.2).Finally,let us show that problem(1.2)has a unique positive solution in the cone

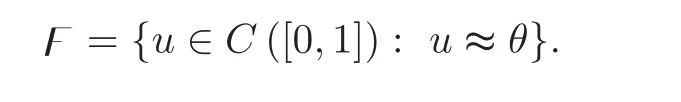
So,we assume thatuandvare arbitrary solutions of problem(1.2)in F.Sinceu,v∈F,then there exists a constantm≥1 such that

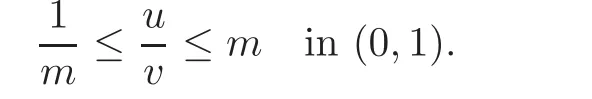
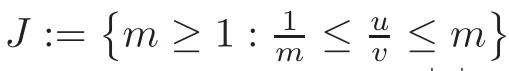
On the other hand,putand then we have

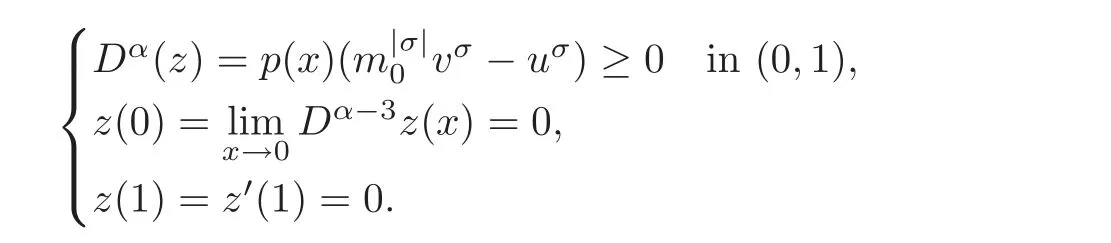
This implies by Proposition 2.2 thatBy symmetry,we obtain thatHence,Using the fact thatm0:=infJand|σ|＜1,we getm0=1.Then,we conclude thatu=v.

To illustrate our result proved in Theorem 1.1,we give the following example.

Example 3.1Letσ∈(−1,1)andpbe a nonnegative continuous function on(0,1)such that

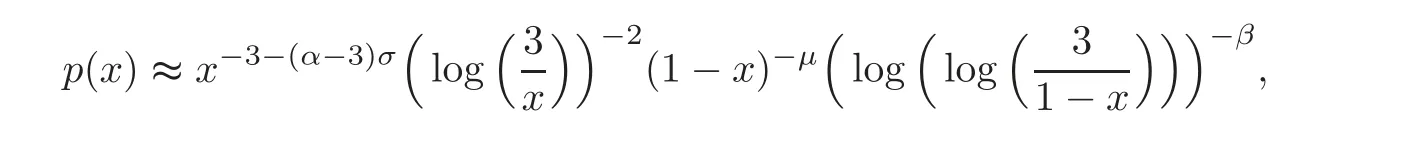
whereμ＜α −1+σandβ∈R.Then by Theorem 1.1,problem(1.2)has a unique positive solutionuinC([0,1])satisfying the following estimates:

(i)Ifμ＜α −2(1− σ)orμ=α −2(1− σ)andβ＞1,then forx∈[0,1],

(ii)Ifμ=α −2(1− σ)andβ=1,then forx∈[0,1],

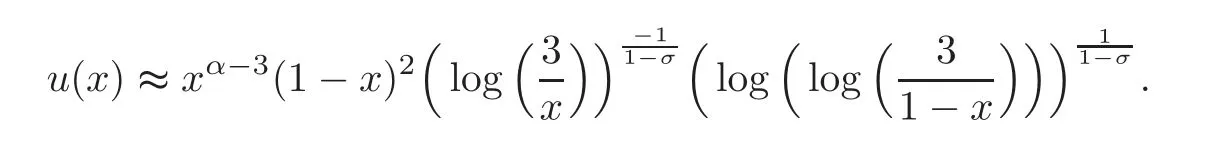
(iii)Ifμ=α −2(1− σ)andβ＜1,then forx∈[0,1],

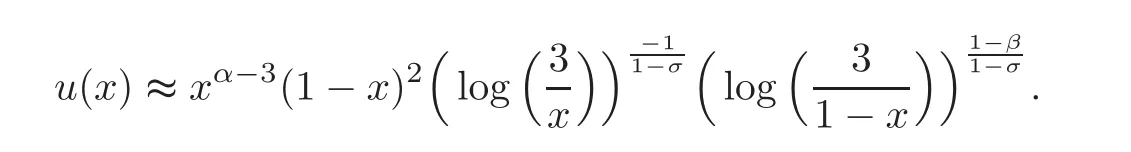
(iv)Ifα−2(1−σ)＜μ＜α−1+σ,then forx∈[0,1],

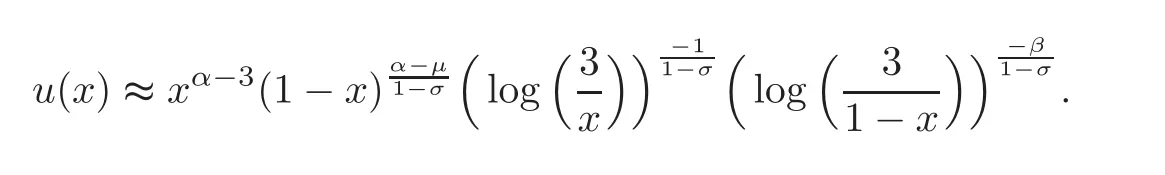
4 Second Existence Result

In this section,we aim at proving Theorem 1.2 and Corollary 1.1.To this end,we need the following preliminary results.For a nonnegative functionqinKαsuch thatαq＜1,we de fine the functionG(x,t)on[0,1]×[0,1]by

whereG0(x,t)=G(x,t)and

Next,we establish some inequalities onGn(x,t).In particular,we deduce thatG(x,t)is well de fined.

Lemma 4.1Let q be a nonnegative function in Kαsuch that αq＜1,and then for each n≥0and(x,t)∈[0,1]×[0,1],we have

(i).In particular,G(x,t)is well de fined in[0,1]×[0,1].

(ii)

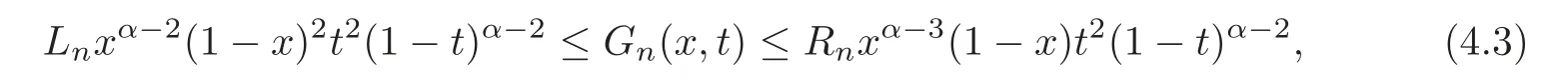
where

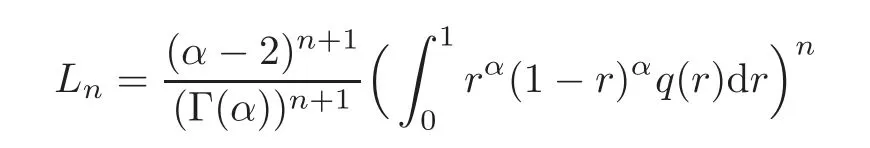
and

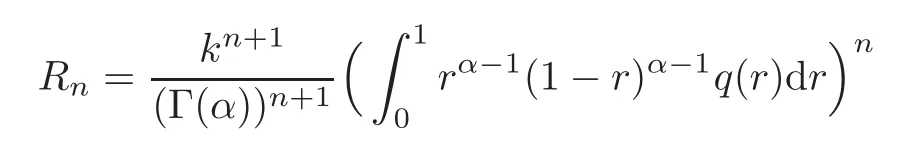
with

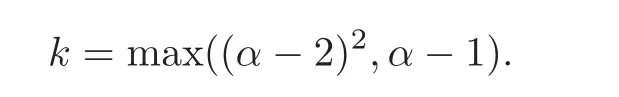
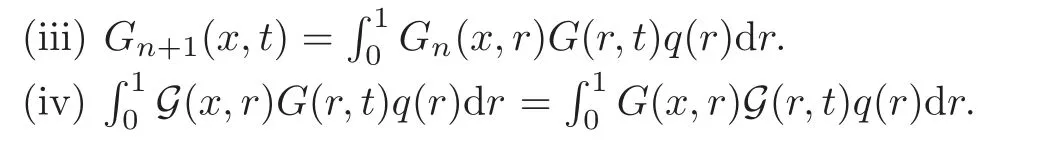
Proof(i)The assertion is clear forn=0.Assume that inequality in(i)holds for somen≥0,and then by using(4.2)and(1.11),we obtain

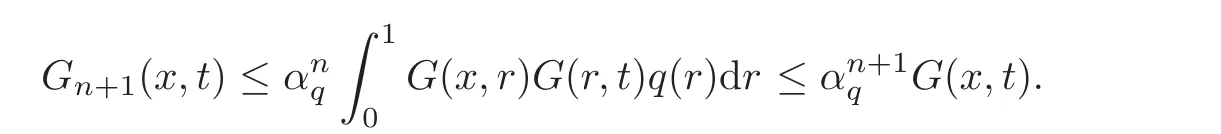
Now,sinceit follows thatG(x,t)is well de fined in[0,1]×[0,1].

(ii)Using Proposition 2.1(ii)and(4.2),we obtain(4.3)by simple induction.

(iii)The equality is clear forn=0.Assume that for a given integern≥1 and(x,t)∈[0,1]×[0,1],we have

Using(4.2)and the Fubini-Tonelli’s theorem,we obtain

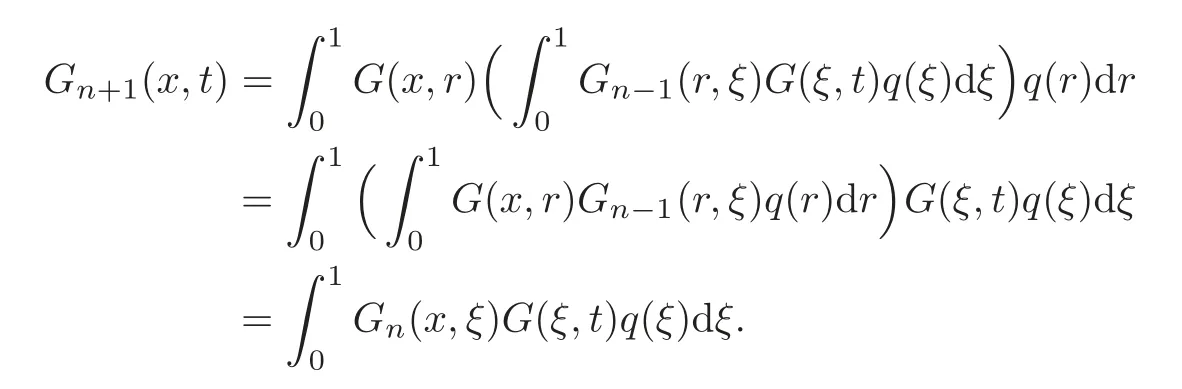
(iv)Letn≥0 andx,r,t∈[0,1],By Lemma 4.1(i),we have

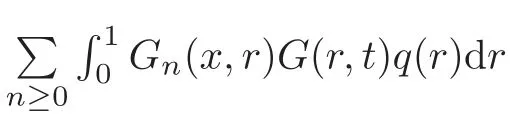
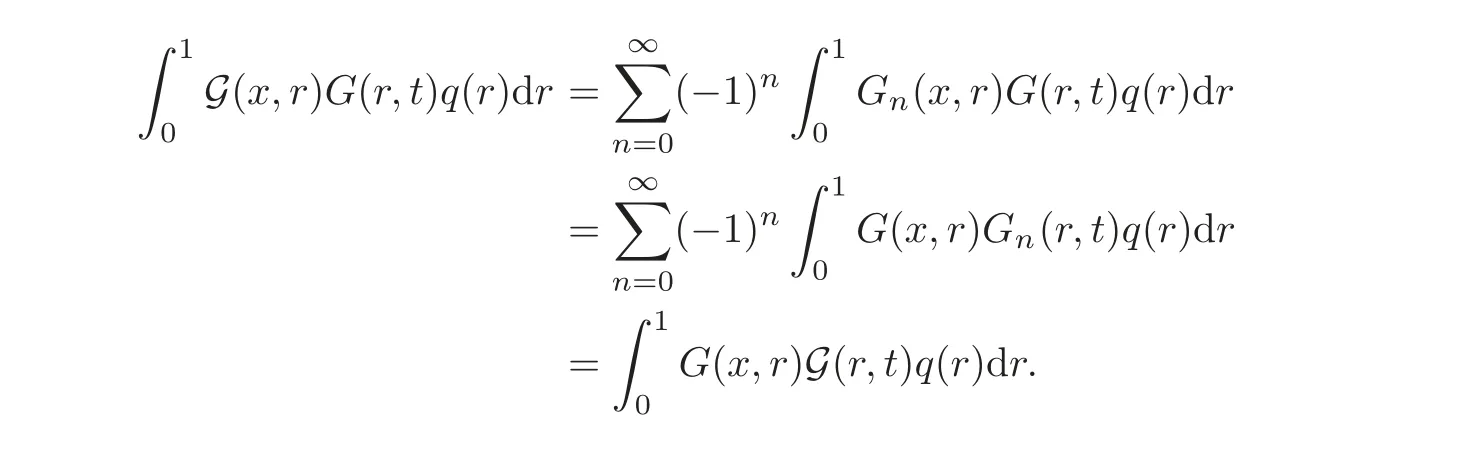
Proposition 4.1Let q be a nonnegative function in Kαsuch that αq＜1.Then the functionis continuous on[0,1]×[0,1].

ProofFirstly,we claim that forn≥0,the functionis continuous on[0,1]×[0,1].The assertion is clear forn=0.Assume that for a given integern≥1,the functionis continuous on[0,1]×[0,1].So,for eachr∈[0,1],the functionis continuous on[0,1]×[0,1].On the other hand,by Lemma 4.1(i)and Proposition 2.1(ii),we have,for each

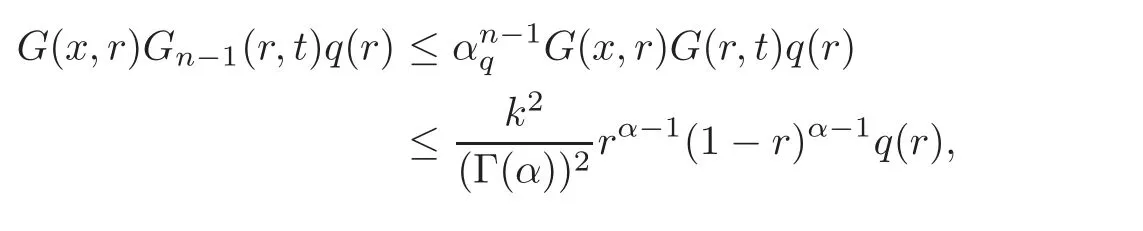
whereSo,we deduce by(4.2)and the dominated convergence theorem that the functionis continuous on[0,1]×[0,1].This proves our claim.Now,by using again Lemma 4.1(i)and Proposition 2.1(ii),we have,for eachx,t∈[0,1],

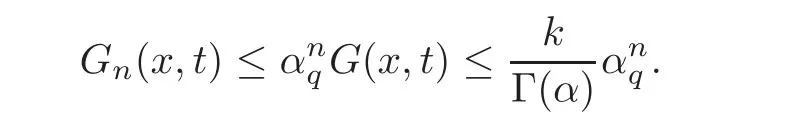
Lemma 4.2Let q be a nonnegative function in Kαsuch thatThen for(x,t)∈[0,1]×[0,1],we have

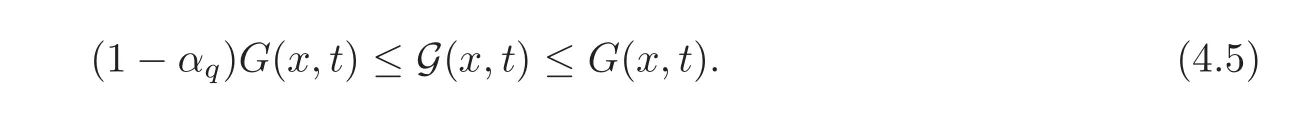
ProofSincewe deduce from Lemma 4.1(i)that

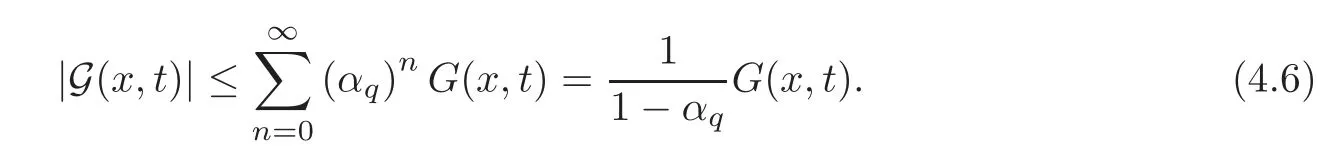
On the other hand,from the expression ofG,we have

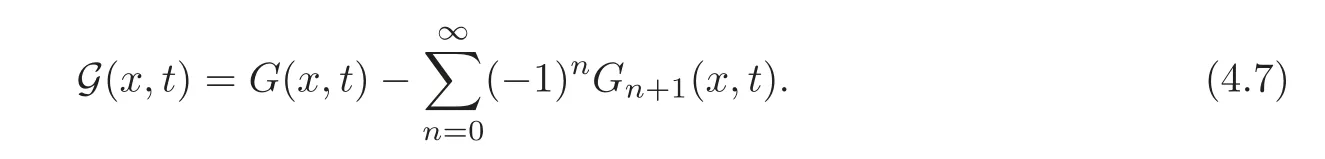
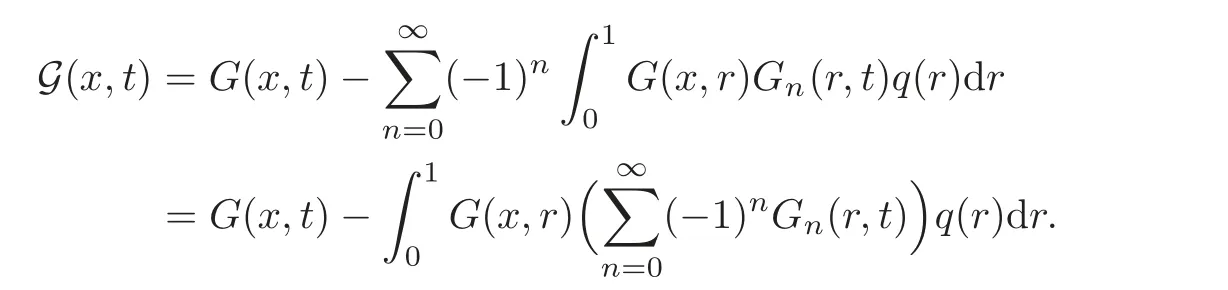
That is

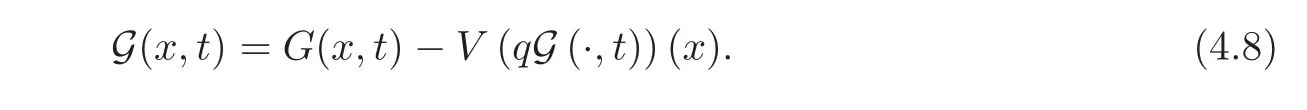
Now,from(4.6)and Lemma 4.1(i)(withn=1),we obtain

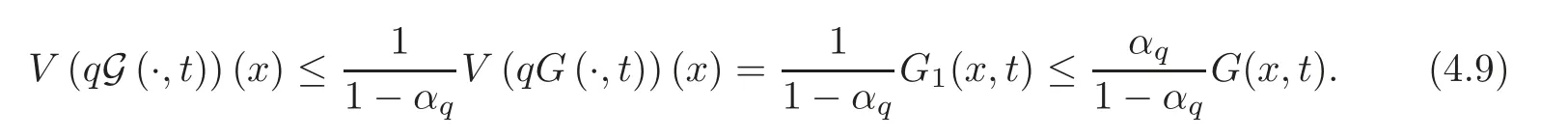
This implies by(4.8)that

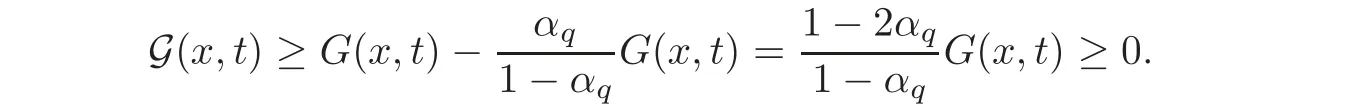
So,it follows that 0≤G(x,t)≤G(x,t)and by(4.8)and Lemma 4.1(i)(withn=1),we have

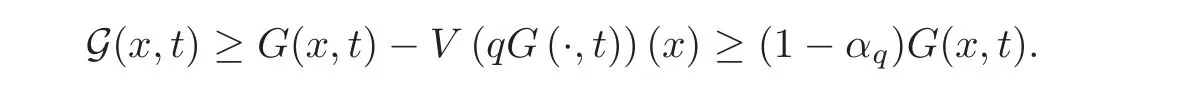
We recall that for a given nonnegative functionsuch thatthe kernelsVandVqare de fined onB+((0,1))by

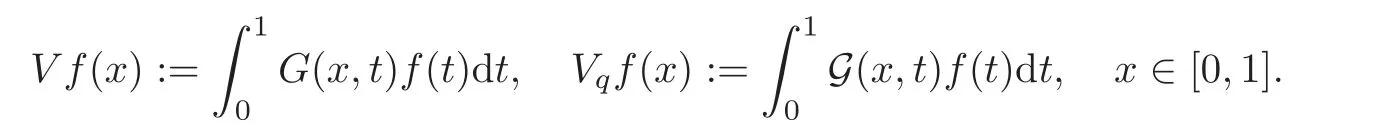
Also let us introduce the kernelV(q.)de fined onB+((0,1))by

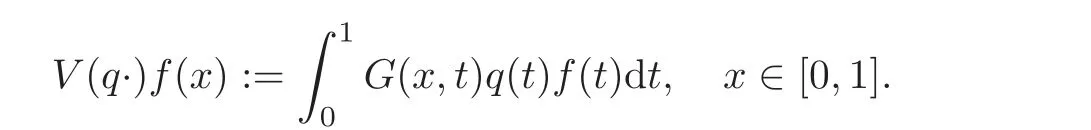
Using Proposition 4.1,(4.5)and Proposition 2.1(ii),we obtain the following corollary.

Corollary 4.1Let q be a nonnegative function in Kαsuch thatand f∈B+((0,1)),and then the following statements are equivalent:

(i)The functionis continuous on[0,1].

Next,we will prove that the kernelVqsatis fies the following resolvent equation.

Lemma 4.3Let q be a nonnegative function in Kαsuch thatandand then Vqf satis fies the following resolvent equation:

In particular,if V(qf)＜∞,we have

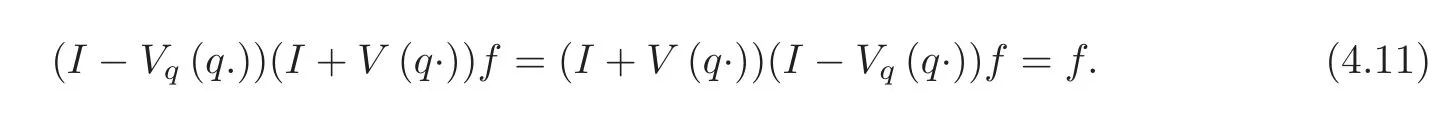
ProofLetand then by(4.8),we have

which implies by the Fubini-Tonelli theorem that forf∈B+((0,1)),

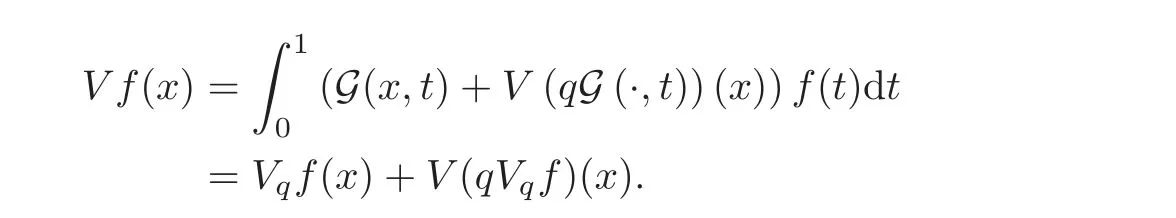
On the other hand,by Lemma 4.1(iii)and the Fubini-Tonelli theorem,we obtain,forf∈B+((0,1))andx∈[0,1],

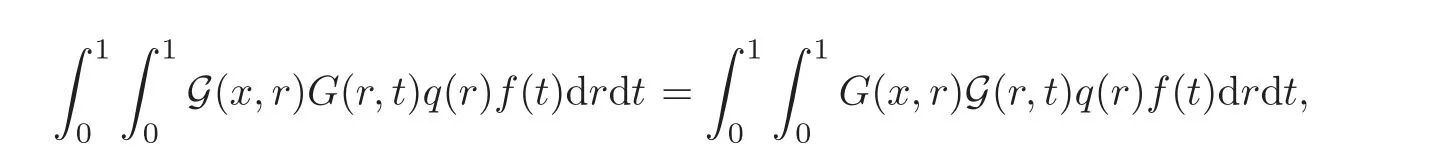
that is,

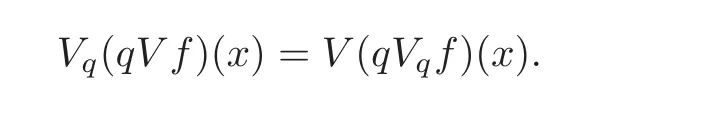
So,we obtain

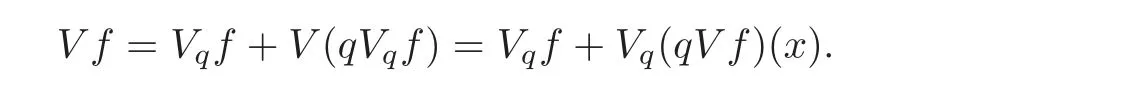
Proposition 4.2Let q be a nonnegative function in Kα∩C((0,1))such thatandsuch thatis continuous and integrable on(0,1).Then is the unique nonnegative solution in C([0,1])of the perturbed fractional problem(1.12)satisfying

ProofSince by Corollary 4.1 the functionis inC([0,1]),it follows that the functionis continuous on(0,1).Using(4.10)and(2.19),there exists a nonnegative constantcsuch that

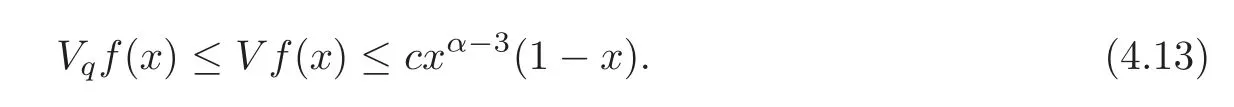
So,we deduce that

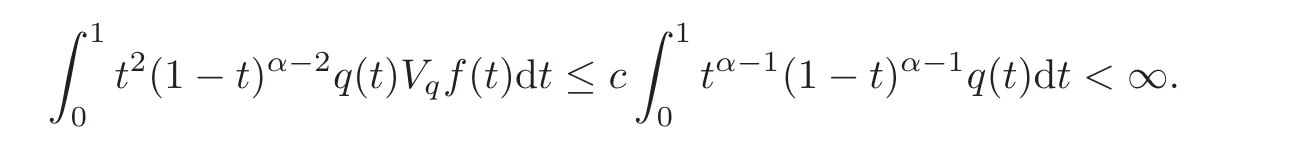
Hence by using Proposition 2.2,the functionsatis fies the equation

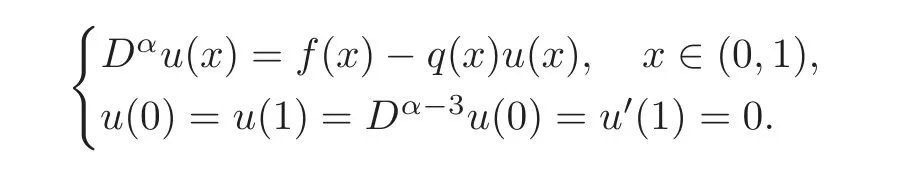
By integrating inequalities(4.5),we obtain(4.12).It remains to prove the uniqueness.Assume thatvis another nonnegative solution inC([0,1])of problem(1.12)satisfying(4.12).Since the functionis continuous on(0,1)and by(4.12)–(4.13),the functionis integrable on(0,1),then it follows by Proposition 2.2 that the function?v:=v+V(qv)satis fies

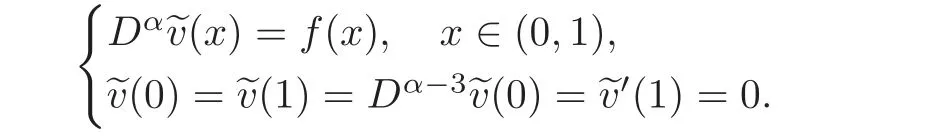
From the uniqueness in Proposition 2.2,we deduce that

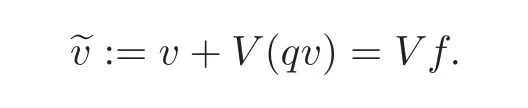
Hence

Now,by(4.12)–(4.13)and(2.23),we have

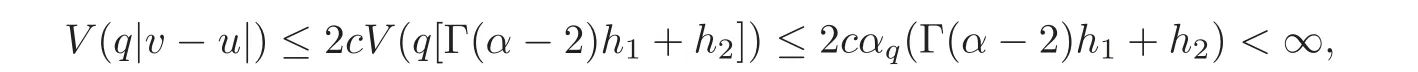
we deduce by(4.11)thatu=v.

Proof of Theorem 1.2Leta≥0 andb≥0 witha+b＞0 and recall that

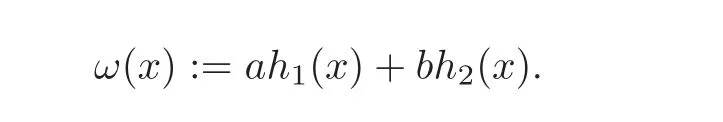
Since the functionϕsatis fies(H2),there exists a positive functionqinsuch thatand for eachx∈(0,1),theis nondecreasing on[0,1].Let

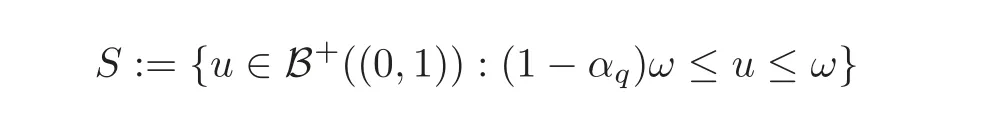
and de fine the operatorLonSby

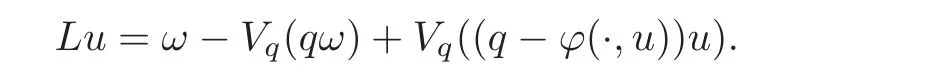
By(4.10)and(2.25),we have

and by(H2)we obtain

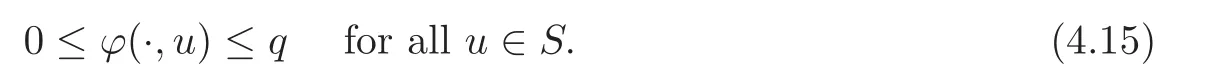
So,we claim thatSis invariant underL.Indeed,using(4.14)–(4.15),we have,foru∈S,

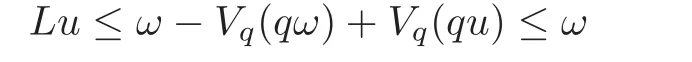
and

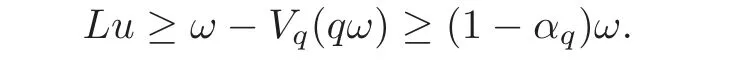
Next,we will prove that the operatorLis nondecreasing onS.Indeed,letu,v∈Sbe such thatu≤v.Since for eachx∈(0,1),the functionis nondecreasing on[0,1],we obtain

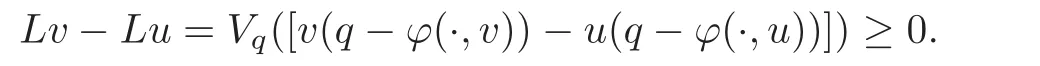
Now,we consider the sequence(un)de fined byandun+1=Lunforn∈N.SinceSis invariant underL,we haveand by the monotonicity ofL,we deduce that

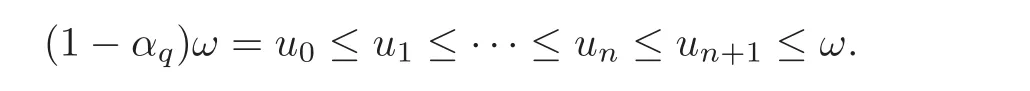
Hence by the dominated convergence theorem and(H1)–(H2),we conclude that the sequence(un)converges to a functionu∈SsatisfyingThat is

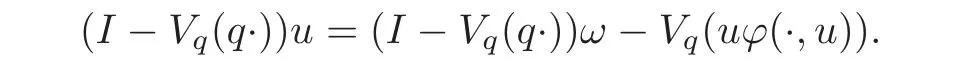
On the other hand,by(4.14),we haveV(qu)≤V(qω)≤ω＜∞,then by applying the operator(I+V(q·))on both sides of the above equality and using(4.10)–(4.11),we conclude thatusatis fies

It remains to prove thatuis a solution of problem(1.7).Using(4.15),there exists a constantc＞0 such that

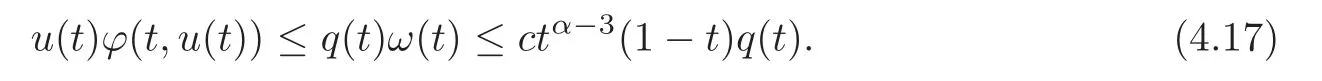
This implies by Corollary 2.1 that the functionis inC([0,1])and so by(4.16),uis inC([0,1]).Now,since by(H1)and(4.17),the functionis continuous and integrable on(0,1),we conclude by Proposition 2.2 thatuis the required solution.It remains to prove that under condition(H3),uis the unique solution to problem(1.7)satisfying(1.13).Assume thatvis another nonnegative solution inC([0,1])to problem(1.7)satisfying(1.13).Sincev≤ω,we deduce by(4.17)that

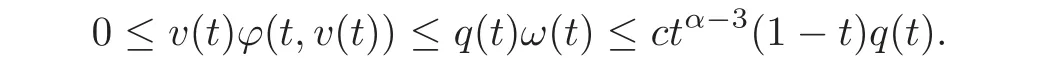
So,the functionis continuous and integrable on(0,1)and by Proposition 2.2,we conclude that the functionsatis fies

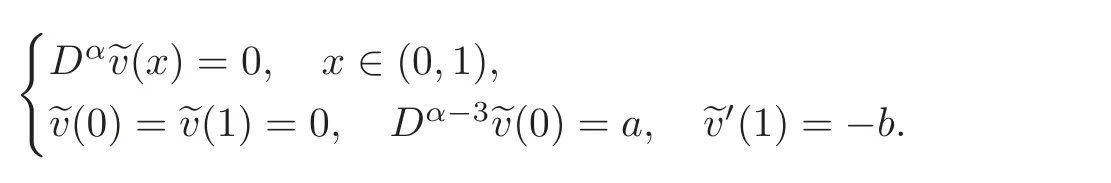
From the uniqueness in problem(1.10),we deduce thatThat is

Now,lethbe the function de fined on[0,1]by

Then by(H3),h∈B+((0,1))and by(4.16)and(4.18),we haveOn the other hand,by(H2),we remark thath≤qand by(2.25)we deduce that

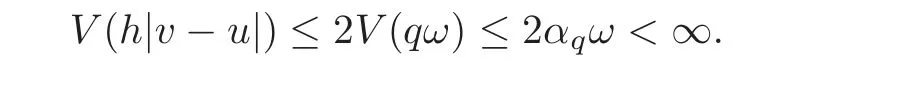
Hence by(4.11),we conclude thatu=v.

Proof of Corollary 1.1LetandIt is clear that hypotheses(H1)and(H3)are satis fied. Since the functionq(x):=λ?p(x)belongs to the classKα,we haveforMoreover,by a simple computation,we obtain

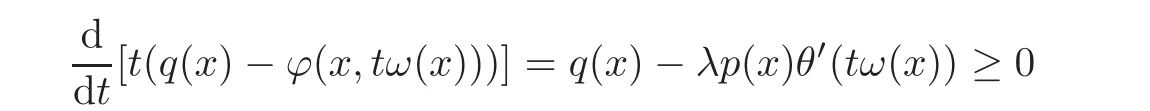
fort∈[0,1]andx∈(0,1).This implies that the functionϕsatis fies hypothesis(H2).So,the result follows by Theorem 1.2.

Example 4.1Let 3＜α≤4 anda,b≥0 witha+b＞0.Letσ≥0,andpbe a positive continuous function on(0,1)such that

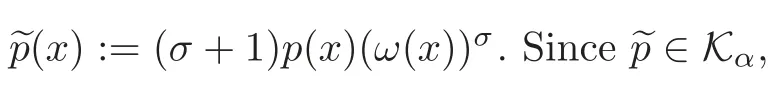
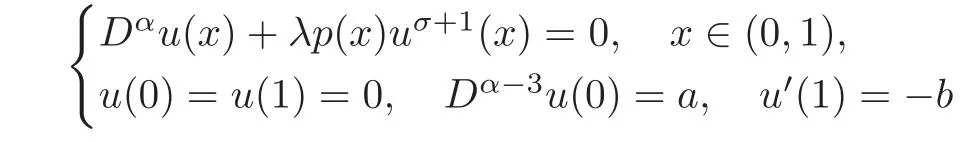
has a unique positive solutionuinC([0,1])satisfying

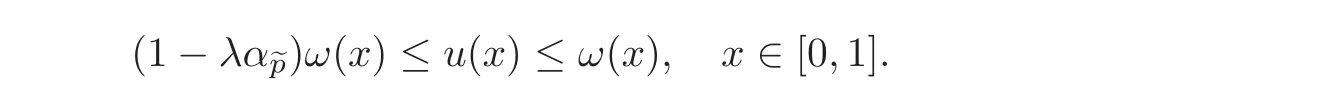
Example 4.2Let 3＜α≤4 anda≥0,b≥0 witha+b＞0.Letσ≥0,γ＞0 andpbe a positive continuous function on(0,1)such that

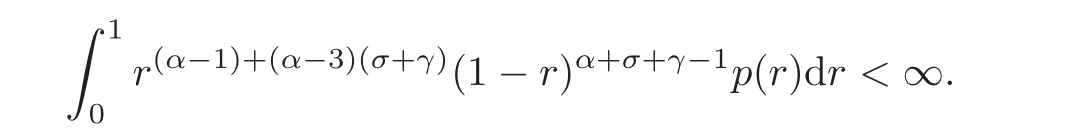
LetandSince,then forthe problem

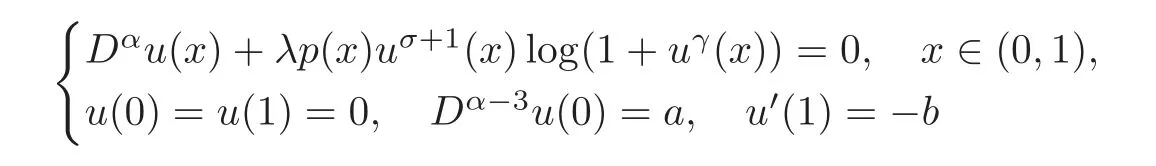
has a unique positive solutionuinC([0,1])satisfying

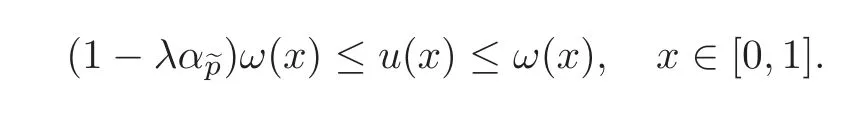
AcknowledgementThe authors want to thank the referees for the careful reading of the paper.

[1]Agarwal,R.P.,O’Regan,D.and Staněk,S.,Positive solutions for Dirichlet problems of singular nonlinear fractional differential equations,J.Math.Anal.Appl.,371,2010,57–68.

[2]Alsaedi,R.S.,Existence and global behavior of positive solutions for some fourth order boundary value problems,Abstr.Appl.Anal.,2014,Article ID 657926,2014,5 pages.

[3]Bachar,I.and M?aagli,H.,Existence of positive solutions for some superlinear fourth-order boundary value problems,J.Funct.Spaces.,2014,Article ID 384958,2014,9 pages.

[4]Bai,Z.and Lü,H.,Positive solutions for boundary value problem of nonlinear fractional differential equation,J.Math.Anal.Appl.,311,2005,495–505.

[5]Chemmam,R.,M?aagli,H.,Masmoudi,S.and Zribi,M.,Combined effects in nonlinear singular elliptic problems in a bounded domain,Advances in Nonlinear Analysis,1,2012,301–318.

[6]Diethelm,K.and Freed,A.D.,On the solution of nonlinear fractional order differential equations used in the modeling of viscoplasticity,Scienti fic computing in Chemical Engineering.II–Computational Fluid Dynamics,Reaction Engineering and Molecular Properties Keil,F.,Mackens,W.,Voss,H.,Werther,J.,eds.,Springer-Verlag,Heidelberg,1999,217–224.

[7]Gaul,L.,Klein,P.and Kemp fle,S.,Damping description involving fractional operators,Mech.Syst.Signal Process.,5,1991,81–88.

[8]Glockle,W.G.and Nonnenmacher,T.F.,A fractional calculus approach of self-similar protein dynamics,Biophys.J.,68,1995,46–53.

[9]Graef,J.R.,Kong,L.,Kong,Q.and Wang,M.,Existence and uniqueness of solutions for a fractional boundary value problem with Dirichlet boundary condition,Electron.J.Qual.Theory Differ.Equ.,55,2013,1–11.

[10]Hilfer,R.,Applications of Fractional Calculus in Physics,World Scientic,Singapore,2000.

[11]Kaufmann,E.R.and Mboumi,E.,Positive solutions of a boundary value problem for a nonlinear fractional differential equation,Electron.J.Qual.Theory Differ.Equ.,3,2008,1–11.

[12]Kilbas,A.A.,Srivastava,H.M and Trujillo,J.J.,Theory and Applications of Fractional Differential Equations,North-Holland Mathematics Studies,204,Elsevier,Amsterdam,2006.

[13]Kilbas,A.A.and Trujillo,J.J.,Differential equations of fractional order:Methods,results and problems.I,Appl.Anal.,78,2001,153–192.

[14]Kilbas,A.A.and Trujillo,J.J.,Differential equations of fractional order:Methods,results and problems.II,Appl.Anal.,81,2002,435–493.

[15]Kristály,A.,R˘adulescu,V.D.and Varga,C.,Variational Principles in Mathematical Physics,Geometry,and Economics:Qualitative Analysis of Nonlinear Equations and Unilateral Problems,Vol.136,Cambridge University Press,Cambridge,2010.

[16]Liang,S.and Zhang,J.,Positive solutions for boundary value problems of nonlinear fractional differential equation,Nonlinear Anal.,71,2009,5545–5550.

[17]Ma,R.and Tisdell,C.C.,Positive solutions of singular sublinear fourth order boundary value problems,Appl.Anal.,84(12),2005,1199–1220.

[18]M?aagli,H.,Mhadhebi,N.and Zeddini,N.,Existence and exact asymptotic behavior of positive solutions for a fractional boundary value problem,Abstr.Appl.Anal.,2013,Article ID 420514,2013,6 pages.

[19]M?aagli,H.,Mhadhebi,N.and Zeddini,N.,Existence and estimates of positive solutions for some singular fractional boundary value problems,Abstr.Appl.Anal.,2014,Article ID 120781,2014,7 pages.

[20]Mainardi,F.,Fractional diffusive waves in viscoelastic solids,Wegner,J.L.,Norwood,F.R.(eds.),Nonlinear Waves in Solids,ASME/AMR,Fair field,1995,93–97.

[21]Mainardi,F.,Fractional calculus:Some basic problems in continuum and statical mechanics,Carpinteri,A.,Mainardi,F.,eds.,Fractals and Fractional Calculus in Continuum Calculus Mechanics,Springer-Verlag,Vienna,1997,291–348.

[22]Marić,V.,Regular variation and differential equations,Vol.1726,Lecture Notes in Mathematics,Springer-Verlag,Berlin,Germany,2000.

[23]Metzler,R.and Klafter,J.,Boundary value problems for fractional diffusion equations,Physica A,278,2000,107–125.

[24]Miller,K.and Ross,B.,An introduction to the Fractional Calculus and Fractional Differential Equations,Wiley,New York,1993.

[25]Podlubny,I.,Fractional Differential Equations,Academic Press,New York,1999.

[26]R˘adulescu,V.D.,Qualitative Analysis of Nonlinear Elliptic Partial Differential Equations,Hindawi Publishing Corporation,2008.

[27]Samko,S.,Kilbas,A.and Marichev,O.,Fractional Integrals and Derivative,Theory and Applications,Gordon and Breach,Yverdon,1993.

[28]Scher,H.and Montroll,E.,Anomalous transit-time dispersion in amorphous solids,Phys.Rev.B,12,1975,2455–2477.

[29]Seneta,R.,Regularly varying functions,Lectures Notes in Math.,Vol.508,Springer-Verlag,Berlin,1976.

[30]Tarasov,V.,Fractional Dynamics:Applications of Fractional Calculus to Dynamics of Particles,Fields and Media,Springer-Verlag,New York,2011.

[31]Timoshenko,S.and Gere,J.M.,Theory of Elastic Stability,McGraw-Hill,New York,1961.

[32]Xu,X.,Jiang,D.and Yuan,C.,Multiple positive solutions for the boundary value problem of a nonlinear fractional differenteial equation,Nonlinear Anal.,71,2009,4676–4688.

[33]Xu,X.,Jiang,D.and Yuan,C.,Singular positone and semipositone boundary value problems of nonlinear fractional differential equations,Mathematical Problems in Engineering,2009,Article ID 535209,2009,17 pages.

[34]Zhang,X.,Liu,L.and Wu,Y.,Multiple positive solutions of a singular fractional differential equation with negatively perturbed term,Mathematical and Computer Modelling,55,2012,1263–1274.