多粒度空间与知识推理*

折延宏，李美丽西安石油大学 理学院，西安 710065



多粒度空间与知识推理*

折延宏+，李美丽
西安石油大学 理学院，西安 710065

SHE Yanhong,LI Meili.Multigranulation space and knowledge reasoning.Journal of Frontiers of Computer Science and Technology,2016,10(6):884-890

摘要：旨在建立起多粒度空间中粗糙近似算子与知识推理中认知算子之间的一一对应关系，从而给出多粒度空间中粗糙近似算子更为合理的语义解释。对于任意逻辑公式，通过分析其语义集与加了认知算子后的语义集之间的关系，证明了全知算子EG对应于多粒度空间中模型AIU中的下近似算子，公共知识认知算子CG对应于模型RU中的下近似算子，分配知识认知算子DG对应于模型RI中的下近似算子，所得结论是模态逻辑与

*The National Natural Science Foundation of China under Grant Nos.61103133,61472471(国家自然科学基金);the Natural Science Foundation of Shaanxi Province under Grant No.2014JQ1032(陕西省自然科学基金);the Scientific Research Program of Education Department of Shaanxi Province under Grant No.15JK1573(陕西省教育厅科技计划项目).

Received 2015-06,Accepted 2015-12.

CNKI网络优先出版:2015-12-29,http://www.cnki.net/kcms/detail/11.5602.TP.20151229.0940.002.html

Pawlak粗糙集之间对应关系在多当事人环境下的推广。关键词：多粒度空间；粗糙近似；知识推理

ISSN 1673-9418CODEN JKYTA8

Journal of Frontiers of Computer Science and Technology

1673-9418/2016/10(06)-0884-07

E-mail:fcst@vip.163.com

http://www.ceaj.org

Tel:+86-10-89056056

1　引言

粒计算[1-3]是一种粒化的思维方式及方法论，其核心概念之一是多层次和多视角粒结构。在多层次粒结构中，基本成分是粒与层，不同层次的粒通过粒度组织起来可以构成一个有序的多层次结构。这样一个多层次结构是对问题的一种描述或观点，称为视角（view）。用多个多层次结构描述同一个问题，将形成多视角（multiview）。多视角代表对问题的不同角度的描述和理解。

作为粒计算的一种具体模型，粗糙集[4-5]自从1982年提出以来受到越来越多学者的研究与关注。特别是近年来，与粒计算所提倡的多层次与多视角思想相适应，一种处理多源信息的多粒度粗糙集模型[6-7]被提出。作为多粒度粗糙集模型的一种等价定义，可以证明在乐观多粒度粗糙集模型中，其上、下近似集是通过对目标对象集在每个Pawlak近似空间下的下近似集取并，对上近似集取交得到的；而在悲观多粒度粗糙集模型中，则是通过对目标对象集在每个Pawlak近似空间下的下近似集取交，对上近似集取并得到的。换言之，已有的多粒度粗糙集模型通过对每个Pawlak近似空间中的粗糙近似结果利用交、并运算进行合成得到，这自然可看作是多粒度空间中一种特殊的信息融合方式。通过进一步考虑基于等价关系的信息融合方式，可给出另外两种不同的粗糙近似方式，最终可给出多粒度空间下一种统一的粗糙近似框架。

将逻辑学方法引入到不确定性信息的处理之中可更好实现基于不同数据库的知识推理，在粗糙集理论中，亦是如此。粗糙集创始人Pawlak提出了粗糙逻辑，并于文献[8]中指出“粗糙逻辑一种基于粗糙集思想的不精确推理逻辑，似乎是一种最为重要的研究课题”。文献[9-11]进一步建立了粗糙集与模态逻辑之间的关系，并给出了若干基于粗糙语义的逻辑推理模型。这种融合粗糙集与逻辑推理为一体的思想理应在多粒度认知环境下得到进一步的延伸，这对基于多粒度信息的不确定性推理有较大的理论意义。

本文正是基于如上考虑，从逻辑学角度给出多粒度粗糙集的描述与刻画。具体为：建立了多粒度近似算子与知识推理中的认知算子之间的密切关系，建立了多粒度空间中不同类型的粗糙近似算子与知识推理中的认知算子之间的对应关系。

本文组织结构如下：第2章给出多粒度空间下粗糙近似的一般框架；第3章介绍知识推理的相关内容；第4章建立多粒度空间下不同粗糙近似模型与知识推理算子之间的对应关系；第5章总结全文。

2　多粒度粗糙集的一般框架

本章通过考虑不同的信息合成方式，给出了多粒度空间下粗糙近似模型的统一框架。在此框架下，定义了两种不同的粗糙集模型，针对每种粗糙集模型，又分别利用集合的交、并运算，给出不同的子模型。

2.1若干基本知识

本节简要给出后续讨论中需要用到的基本知识。

设U为一非空有限集合，称为论域，不失一般性，设U中含有m个元素，在以下讨论中不单独说明。称U×U的任意子集R⊆U×U为U上的一二元关系：

（1）称R为自反的，若对于任意x∈U,有(x,x)∈R；

（2）称R为对称的，若对于任意x,y∈U，如果(x,y)∈R，则(y,x)∈R；

（3）称R为传递的，若对于任意 x,y,z∈U，由(x,y)∈R以及(y,z)∈R，可推得(x,z)∈R；

（4）称R为一等价关系，若R满足自反性、对称性以及传递性。

定义1[12]设R为论域U上的一二元关系，如果有U上的另外一个二元关系R*满足：（1）R*是传递的；（2）R⊆R*；（3）对于U上的任一满足传递性的二元关系R**，若R⊆R**，且R*⊆R**。则称R*为R的传递闭包，记t(R)=R*。

由定义1可以看出，一个关系的传递闭包是包含这个关系的最小的传递关系。

对于一个二元关系R，R的幂次方按照如下方式定义：

由以上归纳定义，特别是式（1），不难验证：

Rk={(x,y)|存在x0,x1,⋃,xk-1,xk,使得x0=x,y=xk,

对于任意j满足0≤j≤k-1,使得(xj,xj+1)∈R}

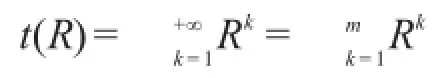
2.2已有的多粒度粗糙集模型

本节简要研究已有的多粒度粗糙集模型，指出这些模型在信息合成方面的特点，这为下一步引入多粒度空间下粗糙近似模型的一般框架做好铺垫。

定义2[6]设U为一非空集合，称为论域，E={R1, R2,⋃,Rn}为论域U上的n个等价关系集，则称二元组(U,E)为一多粒度近似空间。

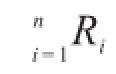
文献[6]首次引入多粒度粗糙集的定义，为了统一起见，本文使用与原文献[6]稍显不同的记号系统。

定义3[6]设(U,E)为一多粒度近似空间，对于任意X⊆U，定义：

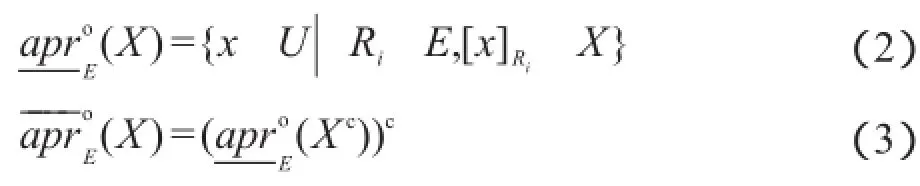
根据定义3可推得：

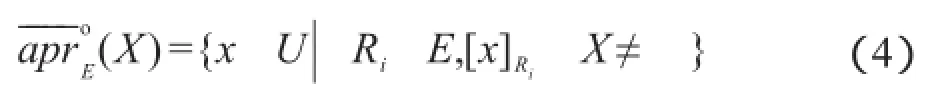
定义4设(U,E)为一多粒度近似空间，对于任意X⊆U，定义：

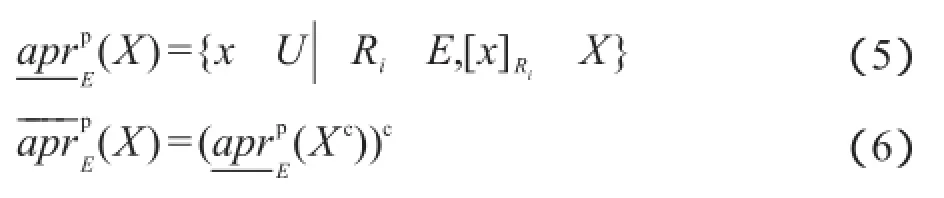
根据定义4可推得：

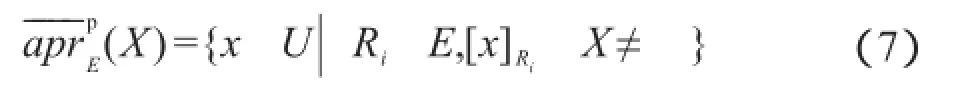
由以上定义可以看得出，在乐观多粒度下近似中，一个对象x属于目标集X的下近似当且仅当存在论域上的一个等价关系使得x在该等价关系下的等价类包含于X，而对于悲观多粒度下近似而言，一个对象x属于目标集X的下近似，当且仅当x在每一个等价关系下的等价类完全包含于X。前者条件宽松，后者条件苛刻，这正是乐观与悲观两词的由来。

定义3、定义4给出了多粒度粗糙集模型具有如下等价形式。

命题2设(U,E)为一多粒度近似空间，则∀X⊆U，

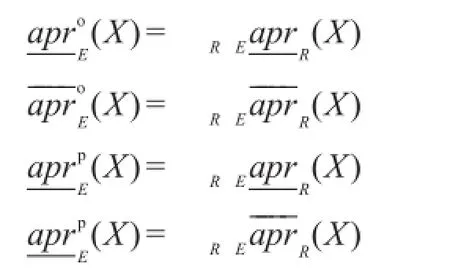
值得注意的是，文献[13]称(U,E)为一多源近似系统，并称由命题2中等价定义的粗糙近似算子为强下近似算子、弱上近似算子、弱下近似算子、强上近似算子。这两种从不同出发点给出的多粒度近似空间中的粗糙近似算子在数学意义下是等价的。

由命题2可知多粒度粗糙集的近似策略：将多粒度近似空间(U,E)看作为n个Pawlak近似空间（或者称为单粒度近似空间）的组合，对于一目标近似集X⊆U，在每个Pawlak近似空间下求得X的上、下近似，然后通过集合论中的并、交运算得到最终的多粒度近似结果。或者说，文献[6,13]给出的多粒度模型是基于对近似结果进行合成的求解策略。

2.3多粒度近似空间中粗糙近似的一般框架

给定一多粒度近似空间(U,E)，以下分别基于对二元关系以及近似结果的合成策略，给出多粒度空间中粗糙近似的一般框架。由此得到的4种粗糙近似模型分别记作模型RI、模型RU、模型AIU以及模型AUI。

（1）模型RI中的粗糙近似

在该模型中，利用集合的交运算将一族等价关系E合成为一个等价关系⋃E。由于等价关系的任意交还是一等价关系，由一个多粒度近似空间(U,E)出发得到了一Pawlak近似空间(U,⋃E)。基于此，可给出模型RI中粗糙上、下近似的定义。

定义5[14]设X⊆U，定义：

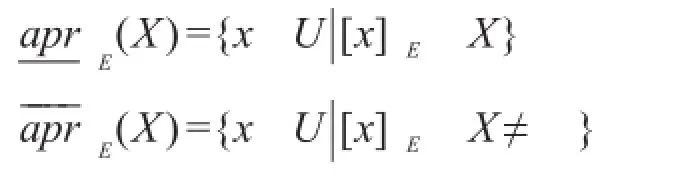
（2）模型RU中的粗糙近似

在该模型中，利用等价关系的传递闭包将一族等价关系E合成为一个等价关系⋃*E。由于等价关系的传递闭包还是一等价关系，由一个多粒度近似空间(U,E)出发得到了一Pawlak近似空间(U,⋃*E)。基于此，可给出模型RU中粗糙上、下近似的定义。

定义6[14]设X⊆U，定义：

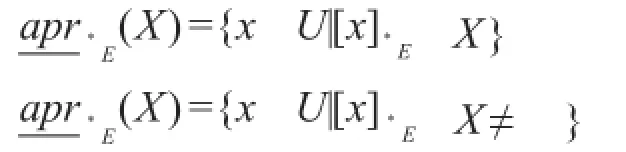
同模型RI与RU不同的是，以下给出的两粗糙近似模型是通过对近似结果（而非等价关系）进行合成得到的。

（3）模型AIU中的粗糙近似

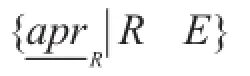
定义7[14]设X⊆U，定义：

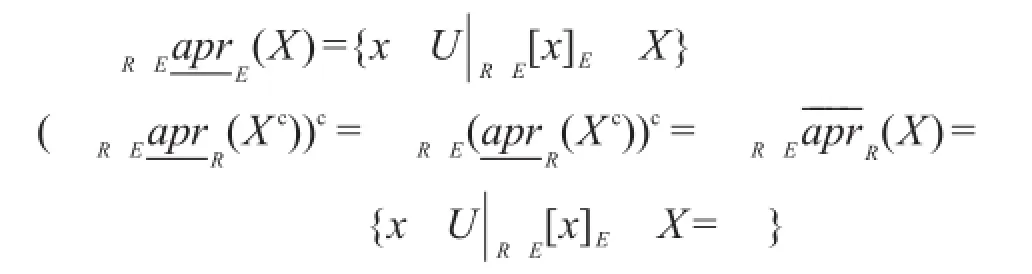
（4）模型AUI中的粗糙近似

与如上类似，通过对下近似集取并集，对上近似集取交集，可定义另外一种不同的多粒度近似空间的粗糙近似模型。

定义8[14]设X⊆U，定义：

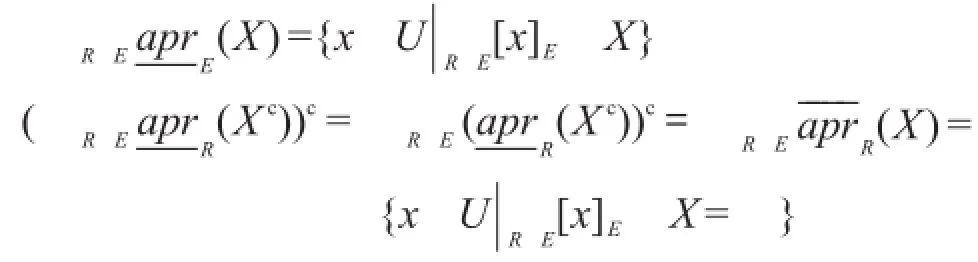
值得注意的是，从不同的信息合成角度出发定义的多粒度空间中的粗糙近似模型AIU与AUI与文献[6]中给出的乐观多粒度与悲观多粒度粗糙集模型是一致的，这由命题2以及定义7、定义8可立即推出。这样本文给出的多粒度空间中粗糙近似的统一框架自然包括了已有的多粒度粗糙集模型。

3　知识推理

文献[15]是一本介绍知识推理的经典著作，这里的知识推理包括对客观知识的推理，也包括对其他当事人知识的推理。同其他逻辑系统一样，知识推理理论包括语构与语义两大部分。

在语构方面，知识推理的语言由公式集组成。用Φ表示原子公式集，¬表示逻辑非，∧表示逻辑合取，K1,K2,⋃,Kn表示与n个当事人所对应的模态算子。记全体逻辑公式为F(S)，它按照如下方式生成：

（1）Φ⊆F(S)；

（2）若φ,ψ∈F(S)，则{¬φ,φ∧ψ,Kiφ}⊆F(S)；

（3）F(S)中任何一逻辑公式均通过（1）、（2）在有限步内生成。

基于¬和∧，可引入如下形式的逻辑连接词：

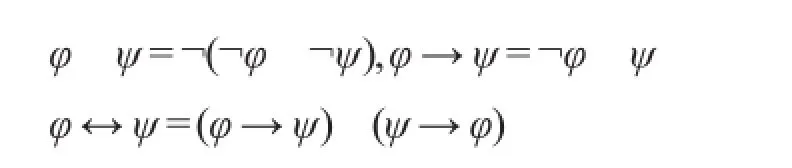
利用如上逻辑语言，可表达一些更为复杂的逻辑公式。如K1K2p∧¬K2K1K2p，它表示第一个当事人知道第二个当事人知道p，而且第二个当事人不知道第一个当事人知道第二个当事人知道p。

除了如上介绍的语构理论之外，知识推理还包括语义理论，即用以判断给定逻辑公式是否为真的形式化模型。知识推理的语义模型是通过可能世界语义定义的，所对应的数学结构被称为Kripke结构。适用于当事人的Kripke结构如下：一n+2元组M= (S,π,κ1,κ2,⋃,κn)，这里S表示一可能世界集（或称状态集），对于S中任一状态s，π(s)为原子公式集上的一赋值映射，即π(s)：Φ→{0,1}。κi是S上的一个二元关系。π(s)(p)告诉人们在状态s下p是否为真。例如p表示“旧金山正在下雨”，则π(s)(p)=1表示在结构M的状态s下，命题“旧金山正在下雨”为真。κi描述的是当事人i的可能关系，(s,t)∈κi表示在当事人i看来，在状态s下，t是可能出现的。在以下讨论中，设κi均为等价关系，用记号(M,s)|=φ表示φ在Kripke结构M的状态s下为真，详细定义如下：

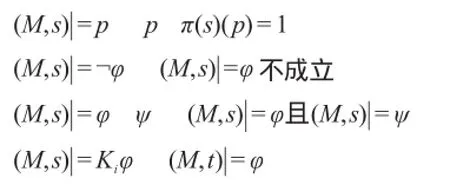
对于满足(s,t)∈κi的所有t成立。

在以上逻辑语言中，无法表达类似于公共知识、分配知识等概念。为此，在如上逻辑语言的基础上，添加如下形式的模态词。如EG（表示G中每个当事人都知道）、CG（表示某个命题是G中所有成员的公共知识）、DG（表示某个命题是G中成员的分配知识），这里G为{1,2,⋃,n}的一个非空子集。自然地，若φ是一逻辑公式，则EGφ、CGφ、DGφ也是逻辑公式。在扩充后的逻辑语言中，可以表达诸如K3¬C1,2p（即第三个当事人知道p不是第一个当事人与第二个当事人的公共知识）的逻辑公式。

以下给出如EGφ、CGφ、DGφ等逻辑公式在Kripke结构下的赋值语言。

全知知识意思是说G中每个当事人都知道的知识，故在Kripke结构中的语义解释为：

(M,s)|=EGφ当且仅当对于任意i∈G，(M,s)|=Kiφ。

对于公共知识而言，CGφ指的是G中每个成员都知道φ，G中每个成员都知道G中每个成员都知道φ等。与此相适应，公共知识在Kripke结构中的语义解释为：

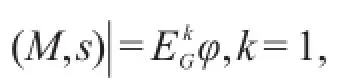
φ是G中成员的分配知识指的是将G中当事人的知识结合起来便可推得φ成立。例如在某Kripke结构中，在状态s下，第一个当事人认为s、t是可能发生的，而第二个当事人认为s、u是可能的。结合这两个当事人的知识便知在状态s下，只有s是可能的。一般来讲，通过消除G中当事人认为不可能的状态便可达到结合G中当事人知识的目的。在数学上，这个通过对在同一状态下不同当事人认为可能的状态集进行取交得到，即：

(M,s)|=DGφ当且仅当对于任意(M,t)|=φ对于满足(s,t)∈∩i∈Gκi的任意t都成立。

4　知识推理与多粒度近似空间

本章基于知识推理中的语义理论，建立起知识推理中的模态算子与多粒度近似空间下近似算子之间的密切联系，这种联系自然是文献[9]中有关粗糙集与模态逻辑在多当事人环境下的推广。

定义9设M=(S,Φ,κ1,κ2,⋃,κn)为一Kripke结构，则对于任意φ∈F(S)，定义：

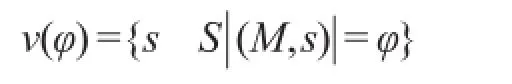
称v(φ)为φ的真状态集。

命题3设M=(S,Φ,κ1,κ2,⋃,κn)为一Kripke结构，则对于任意φ∈F(S)，有：

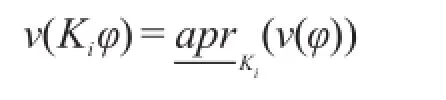
证明 类似证明在文献[9]中给出，略。

命题说明知识推理中的模态词κi对应于Pawlak粗糙下近似算子。

命题4设M=(S,Φ,κ1,κ2,⋃,κn)为一Kripke结构，则对于任意φ∈F(S)，有：

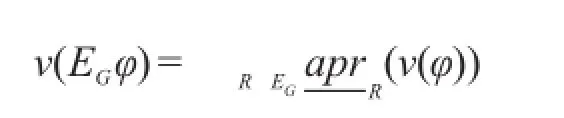
这里EG={κi|i∈G}。

证明 根据定义，有：

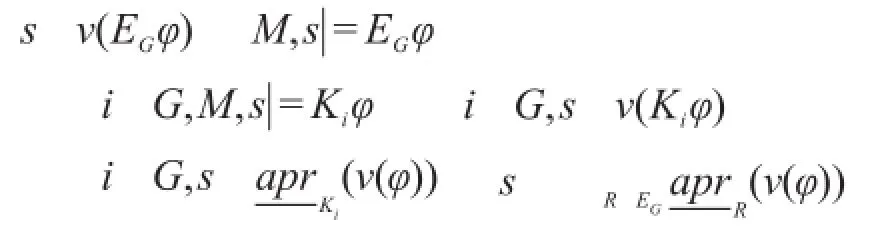
即可得证。

命题4说明知识推理中的全知模态词对应于多粒度近似空间中AIU模型中的粗糙下近似算子。

命题5设M=(S,Φ,κ1,κ2,⋃,κn)为一Kripke结构，则对于任意φ∈F(S)，有：

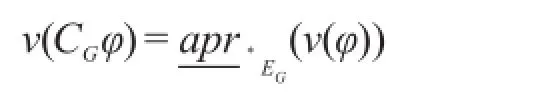
这里EG={κi|i∈G}。

为证明命题5，需要如下引理。

引理1设EG={κi|i∈G}，则对于任意(s,t)∈⋃*EG，存在自然数 k≥1以及状态序列 s0,s1,⋃,sk使得s0=s,t=sk，且对于满足0≤j≤k-1的任意 j，存在i∈G使得(sj,sj+1)∈κi。

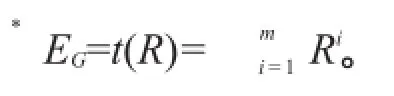
引理2设M=(S,Φ,κ1,κ2,⋃,κn)为一Kripke结构，s∈S,φ∈F(S)，则s对于任意满足如下条件（*）的任意t∈S，有M,t|=φ。

（*）存在状态序列s0,s1,⋃,sk使得s0=s，t=sk，且对于满足0≤j≤k-1的任意 j，存在i∈G使得(sj,sj+1)∈κi。

证明 根据M,s|=EGφ的定义，并通过对k进行归纳可以证明。

以下证明命题5。

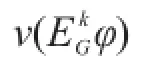
命题6设M=(S,Φ,κ1,κ2,⋃,κn)为一Kripke结构，则对于任意φ∈F(S)，有：

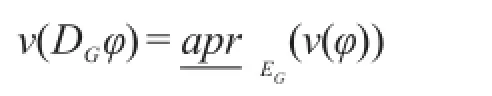
这里EG={κi|i∈G}。

证明根据定义可立即推出。

本章结论可通过表1来表示。

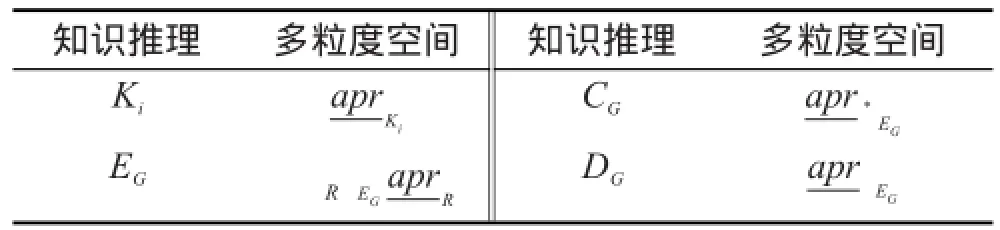
Table 1 Relationship between knowledge reasoning and multigranulation space表1　知识推理与多粒度空间的对应关系

5　结束语

粗糙集近似算子与模态逻辑算子之间的对应关系在文献[9]中已有论述，那里的讨论仅局限于单粒度粗糙集与含有一个模态算子的模态逻辑。本文则是将在信息表达能力更强的多粒度近似空间与容纳多个客体的知识推理中建立起类似的对应关系。主要结论是知识推理中的全知算子对应于文献[6]中提出的悲观下近似算子，即本文统一框架AIU模型中的下近似算子，公共知识算子对应于基于传递闭包的下近似算子，分配知识算子对应于基于等价关系交的下近似算子。这些结论为从逻辑角度研究多粒度粗糙集提供了新的思路与方法。

不难看出，若在知识推理中基于模态算子Ki定义其对偶算子以及全知算子的对偶算子，则所定义的算子自然对应于多粒度粗糙集中的悲观上近似算子。由于模态逻辑与三值逻辑有密切的关系，在后续工作中，进一步从三值逻辑的角度研究多粒度粗糙集。

References:

[1]Lin T Y,Yao Yiyu,Zadeh L A.Data mining,rough sets and granular computing[M].Berlin:Springer Science Business Media,2002.

[2]Yao Yiyu.Perspectives of granular computing[C]//Prceedings of the 2005 IEEE International Conference on Granular Computing.Piscataway,USA:IEEE,2005,1:85-90.

[3]Yao Yiyu.The art of granular computing[M]//Rough Sets and Intelligent Systems Paradigms.Berlin,Heidelberg: Springer,2007:101-112.

[4]Pawlak Z.Rough sets[J].International Journal of Computer and Information Science,1982,11(5):341-356.

[5]Pawlak Z.Rough sets—theoretical aspects of reasoning about data[M].Hingham,USA:KluwerAcademic Publishers,1991.

[6]Qian Yuhua,Liang Jiye,Yao Yiyu,et al.MGRS:a multigranulation rough set[J].Information Sciences,2010,180 (6):949-970.

[7]Qian Yuhua,Liang Jiye,Dang Chuangyin.Incomplete multigranulation rough set[J].IEEE Transactions on Systems, Man and Cybernetics:PartASystems and Humans,2010,40 (2):420-431.

[8]Pawlak Z,Grzymala-Busse J,Slowinski R,et al.Rough sets[J]. Communications of theACM,1995,38(11):88-95.

[9]Yao Yiyu,Lin T Y.Generalization of rough sets using modal logics[J].Intelligent Automation Soft Computing,1996,2 (2):103-119.

[10]Banerjee M,Chakraborty M K.Rough sets through algebraic logic[J].Fundamenta Informaticae,1996,28(3):211-221.

[11]She Yanhong,He Xiaoli,Wang Guojun.Rough truth degrees of formulas and approximate reasoning in rough logic[J]. Fundamenta Informaticae,2011,107(1):67-83.

[12]Wang Guojun.Computation intelligence:computing with wordsandfuzzyset[M].Beijing:HigherEducationPress,2005.

[13]Khan M A,Banerjee M.Formal reasoning with rough sets in multiple-source approximation systems[J].International Journal ofApproximate Reasoning,2008,49(2):466-477.

[14]Yao Yiyu,She Yanhong.Rough set models in multigranulation spaces[J].Information Sciences,2016,327:40-56.

[15]Halpern J Y,Moses Y,Vardi M Y.Reasoning about knowledge[M].Cambridge,USA:MIT Press,1995.

附中文参考文献:

[12]王国俊.计算智能(第二册)：词语计算与Fuzzy集[M].北京:高等教育出版社,2005.

SHE Yanhong was born in 1983.He received the Ph.D.degree in fundamental mathematics from Shaanxi Normal University in 2010.Now he is an associate professor at Xi’an Shiyou University.His research interests include uncertainty reasoning and granular computing,etc.

折延宏（1983—），男，陕西延安人，2010年于陕西师范大学获得博士学位，现为西安石油大学副教授，主要研究领域为不确定性推理，粒计算等。

LI Meili was born in 1975.She received the Ph.D degree in navigation,guidance and control from Northwestern Polytechnical University in 2010.Now she is a lecturer at Xi’an Shiyou University.Her research interests include granular computing and image processing,etc.

李美丽（1975—），女，陕西渭南人，2010年于西北工业大学获得博士学位，现为西安石油大学讲师，主要研究领域为粒计算，图像处理等。

+Corresponding author:E-mail:yanhongshe@gmail.com

文献标志码：A

中图分类号：TP18

doi:10.3778/j.issn.1673-9418.1506014

Multigranulation Space and Knowledge Reasoningƽ

SHE Yanhong+,LI Meili
College of Science,Xi’an Shiyou University,Xi’an 710065,China

Abstract:This paper aims at establishing a one-to-one correspondence between rough approximation operators in multigranulation space and epistemic operators in knowledge reasoning,and thus providing a more reasonable semantic interpretation for rough approximation operators in multigranulation space.By deeply analyzing the close relationship between the semantic set of a logic formula and that of the formula obtained by adding different epistemic operators,this paper proves that EG,CG,DGare in one-to-one correspondence with rough lower approximation operator in model AIU,rough lower approximation operator in model RU and rough lower approximation operator in model RI,respectively.The obtained results are the generalization of the relationship between modal logic and Pawlak rough set in multi-agent environment.

Key words:multigranulation space;rough approximation;knowledge reasoning