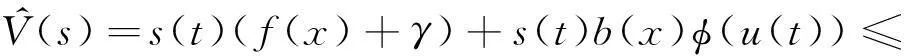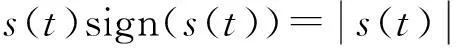具有死区输入的不确定混沌系统控制

谢玉姣，林　达，边潇俊

(四川理工学院 自动化与电子信息学院，四川 自贡　643000)



具有死区输入的不确定混沌系统控制

谢玉姣，林达，边潇俊

(四川理工学院 自动化与电子信息学院，四川 自贡643000)

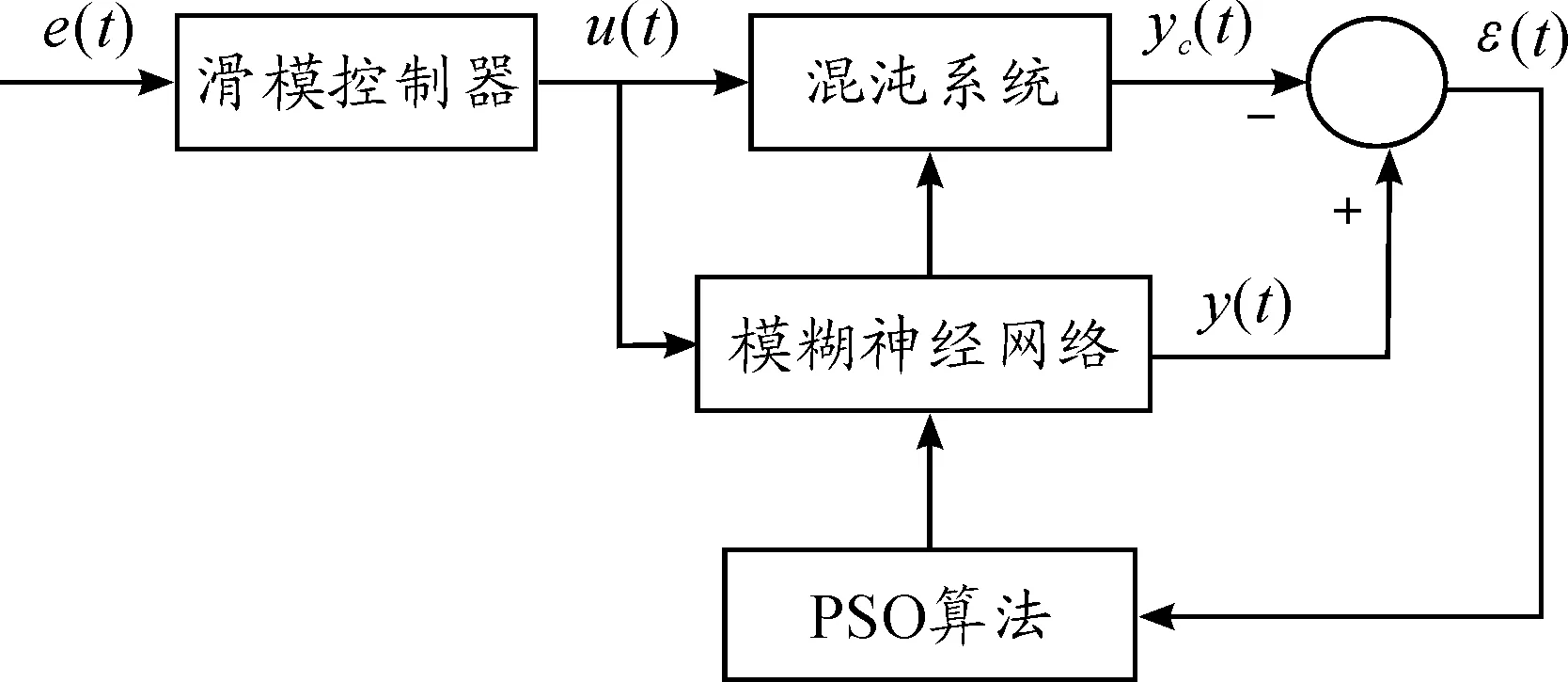
摘要：死区输入存在于大部分工业控制系统中，对控制系统的性能有较大的影响。针对具有死区、非线性控制输入的不确定混沌系统，利用模糊神经网络的逼近能力，在对不确定混沌系统进行辨识的同时，自适应地补偿其非光滑、非线性的特性。为了提高模糊神经网络的性能，使辨识误差最小，利用粒子群优化算法对模糊神经网络的参数进行优化，从而使逼近误差达到最小。在系统的控制部分，采用滑模控制对输入的信号进行跟踪控制。最后对Duffing系统进行仿真，并与传统控制方法做比较，证明了该方法的有效性和优越性。

关键词：死区输入；模糊神经网络；粒子群算法；滑模控制

对具有死区、非线性控制输入的不确定混沌系统进行识别控制是当前具有挑战性的一项研究。混沌是确定性非线性系统中出现的一种不规则的、随机的现象，其对系统初始状态非常敏感，即使一个极小的外界扰动，系统状态就可能产生很大的改变[1]。最早进行混沌研究的是法国的庞加莱，他于1913年提出三体问题在一定范围内的解是随机的，即保守系统中的混沌理论。1927年，B.Van der Pol发现了“不规则的噪声”。1954年，Kolmogorov提出了KAM定理的雏形。1963年，气象学家洛伦兹提出“决定论非周期流”的观点，并给出了著名的洛伦兹方程，揭开了混沌理论研究的序幕。随着非线性科学和混沌理论的发展，混沌在电子学、天体力学、信息科学等领域都有广阔的应用。

混沌控制的目标可分为两种：1) 基于OGY思想的混沌控制，这是一种离散控制技术，即对混沌系统施加小的扰动，以使受控系统稳定到期望的轨道上。其特点是：控制信号小，不破坏混沌系统的内在特性，抑制混沌的同时又利用混沌；其缺点是：等待时间较长、噪声环境下易失控；2) 基于非线性系统的控制方法，主要目的在于消除混沌以获得期望的新的动力学行为。例如：控制混沌系统跟踪一个给定的参考信号或到达期望的不稳定平衡点上，其特点是：破坏了混沌的内在特性，控制能量相对较大[2]。由于大多数现实中的混沌系统具有内在的未知非线性和参数不确定性，不可能构造精确的数学模型来描述，传统的控制方法已无法对其进行有效的控制，因此，出现了以模糊神经网络为基础的智能控制技术。

然而，尽管众多学者已对混沌控制进行了深入的研究，但是对具有非光滑(如死区、后冲、迟滞以及饱和等)、非线性控制输入的不确定混沌系统的控制问题的研究成果较少。这类混沌系统普遍存在于工业控制系统中，且通常是时变的并限制了系统的性能。其中，死区在工业生产过程中是最重要的影响因素之一，死区的出现会严重影响系统的性能，因此，它一直是科学家们研究的热点问题[3-15]。为解决死区问题，文献[6]提出了针对具有死区输入的多输入多输出非线性系统，基于Nussbaum function的神经网络识别方法，文献[5,10]提出了自适应死区补偿控制的方法。其中，文献[5]将RBF神经网络与模糊逻辑结合，对死区输入进行补偿；文献[10]提出了自适应动态RBF神经网络，通过与控制器并联实现控制的目的；文献[12]提出了一种针对一般非线性、未知死区宽度的补偿方法；文献[13]通过对参考模型给定一个匹配条件，介绍了自适应死区逆的智能控制方法；文献[7]提出了输出自适应反馈控制，其针对单输入单输出未知死区输入的非线性系统，利用反馈和平滑的反转函数实现。随着模糊逻辑和神经网络技术的发展，利用模糊逻辑或神经网络识别非线性系统的参数成为学者研究的焦点，模糊神经网络集合了二者的优点，具有全局逼近性和收敛速度快、鲁棒性强等特点[15]。例如，文献[8]和[9]提出了模糊控制的方法，其中文献[8]结合了变结构自适应模糊控制，文献[9]提出了基于遗传算法的模糊控制方法。

由于具有死区输入的不确定混沌系统无法精确建模，故本文选择利用模糊神经网络对该系统进行辨识，并结合粒子群算法对网络参数进行优化；然后，利用滑模控制器进行跟踪控制；最后，通过对Duffing混沌系统的仿真实验，说明本文提出的控制方法的优越性能。

1系统模型

具有死区输入的不确定混沌系统可表示为

其状态空间形式可表示为

(1)

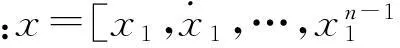
(2)

其中：φ+(·)和φ-(·)为未知的光滑连续非线性函数；u+和u-均为正常数[3]。非线性死区模型如图1所示。

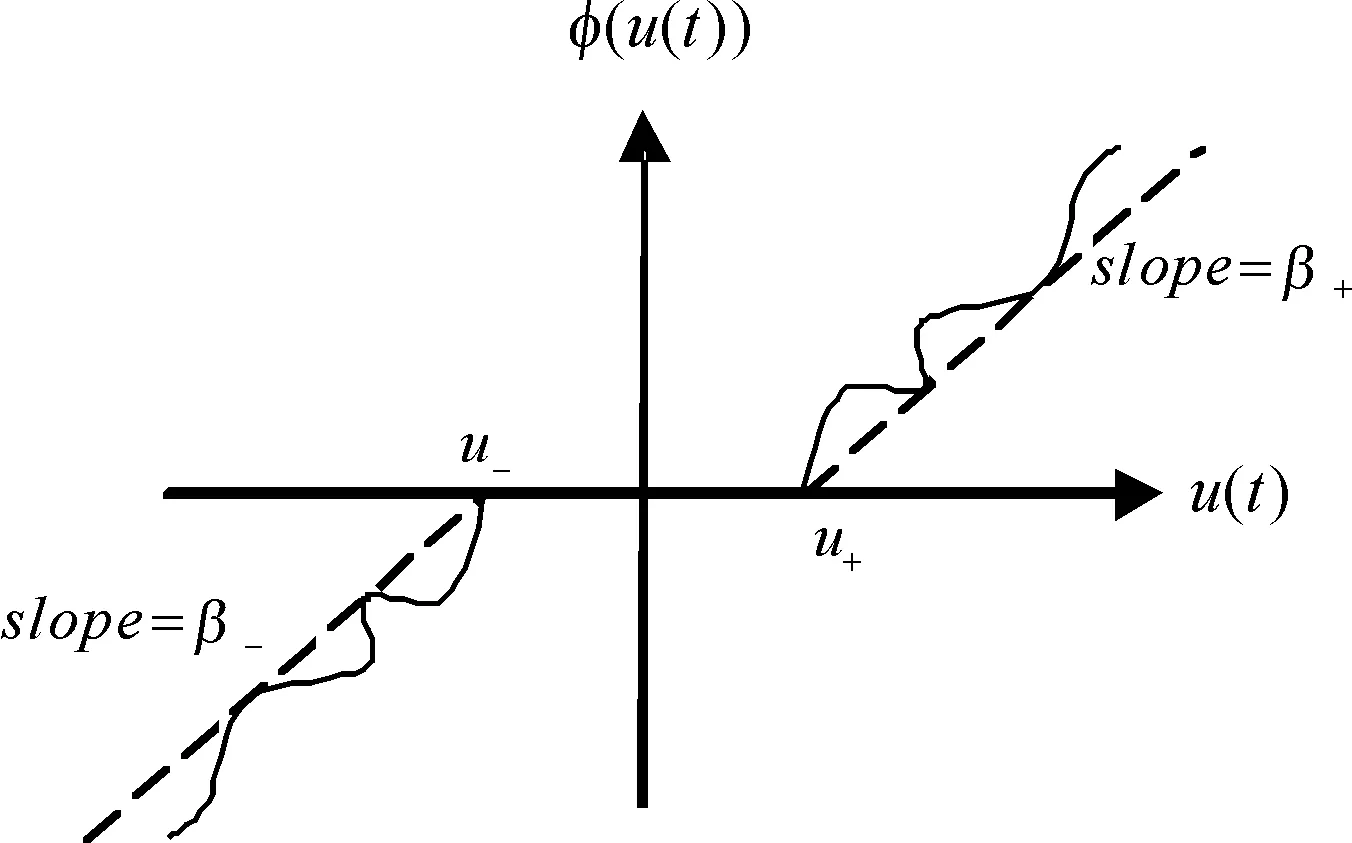
图1　非线性死区模型

φ(u(t))满足如下关系：

(3)

其中：β+和β-均为正常数，且β+≤φ+(·)，β-≤φ-(·)。

本文的目标是结合优化的模糊神经网络，设计一个滑模控制器u(t)，实现具有死区输入的非线性不确定混沌系统的跟踪控制，使跟踪误差e最小。若期望轨迹为yd，则跟踪误差e为

e=x-yd=x-xd

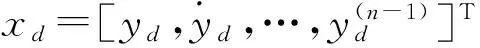
(4)

(5)

1) 0

2)U≤umax,且β≥βmin；

2TSK模糊神经网络

TSK模糊模型由模糊规则组成，即

THENθl(k)=gl(u(k))

其中：R(l)为第l条模糊规则；u(k)=[u1(k),u2(k),…,un(k)]T为模型在时刻k的输入矢量；θl(k)为第l条规则的输出。TSK模糊模型如图2所示。

图2　TSK模糊模型

第一层为输入层，节点代表输入变量；第二层为隶属度函数层，本文选为高斯函数；第三层为模糊规则层，每个节点代表1条模糊规则，所有节点组成1个模糊集合；第四层为输出层，其节点输出为：

则式(6)可表示为

(8)

其中：θT=[θ1,…,θM]；ζT(u)=[ζ1(u),…,ζM(u)]。对未知函数f(x)的辨识转化为对参数向量θ的辨识问题[11]，混沌系统辨识框图见图3。

图3　混沌系统辨识框图

3粒子群优化算法

粒子群算法即粒子群优化算法(particle swarm optimization，PSO)，最初由Kennedy和Eberhart提出。这种算法源于鸟群和鱼群的社会行为，可用于优化复杂的数值函数。简单地说，粒子群算法是一种基于群体智能的进化算法。种群由个体组成，即粒子，粒子的位置随时间的变化而改变。搜索空间中的每个粒子代表优化问题的一个解，它们在一个多维的搜索空间里运动。在运动过程中，每个粒子根据自身的经验和相邻粒子的经验调整位置，以到达最佳位置，最终粒子群将移动到最优的多维搜索空间区域，即从当前搜索的局部最优值寻找全局最优。每个粒子的性能通过适应度函数值测定，适应度函数的选择由具体问题来确定[16]。粒子群算法在解决非线性非光滑、不确定系统问题方面具有鲁棒性较强、收敛快、实现简单的特点，其数学理论和算法步骤如下：

设D维空间粒子i的当前位置为Xi=(xi1,…,xid,…,xiD)，飞行速度为Vi=(vi1,…,vid,…,viD)，其最优位置表示为Pi=(pi1,…,pid,…,piD)，也可记为pbest，整个种群中最优的pbest记为Pg，即gbest，且D的值等于模糊规则数，即D=M。粒子的飞行速度和位置可动态调整，其更新方程如下：

其中：w为权重系数，值为[0,1]上的任意数；c1、c2为学习速率，其值为正常数；r1、r2为[0,1]上的随机数。本文算法的终止条件为判断是否满足规定的最大种群数，适应度函数为

(11)

其中：f(x)为适应度函数；ε(t)为辨识误差；yc(t)为系统参考输出；y(t)为模糊神经网络的输出，可由式(6)算出，其中w替换为粒子的位置向量。

步骤2速度和位置修正：利用式(3)、(4)来修正每个粒子的速度和位置；

步骤3利用适应度函数更新局部最优值：计算每个粒子的适应度值，其最优适应度值按式(11)更新，如果f(Xi)>f(Pi)，那么pid=xid；

步骤4更新全局最优值；

步骤5返回步骤2。

4滑模控制

滑模控制是一种变结构高速开关控制，它能使系统状态轨迹保持在指定的滑动面上。设计滑模控制器包含2个步骤：① 选择合适的滑动面；② 计算控制律以确保滑动面的稳定性[3]。为保持式(5)稳定，本文选择如下李雅普诺夫函数：

(12)

其导数为

(13)

定义控制律为

(14)

由式(13)可知

(15)

当s(t)<0时，由式(3)和(14)知：u(t)>u+，

(16)

当s(t)>0时，由式(3)和(14)知：u(t)

(17)

即

(18)

将式(18)代入式(16)，得

(19)

图4　轨迹跟踪控制器框图

5仿真

为证明本文提出控制方法的有效性，对本文Duffing系统进行仿真实验。

令φ+(u(t))=1-0.3sin(u(t))，φ-(u(t))=0.8-0.3cos(u(t))，λ=3，期望轨迹为yd=sin(t)，且b0=0.5,b1=1.5,umax=0.5,βmin=0.5。 Duffing系统的初始状态定为x1(0)=-1,x2(0)=0.5。本文的模糊神经网络规则数取9，采样时间为0.01 s，学习速率c1=1.9，c2=0.8，种群规模为50，迭代次数为300，计算步长为1 000，Vi∈[-2,2]，仿真结果如图5～8所示。

图5　Duffing混沌系统相平面图

图6　系统识别误差

图7　轨迹跟踪曲线

图6(a)为引入粒子群优化算法的识别误差图，(b)为未引入粒子群优化算法的误差图，由图可知：在引入粒子群优化算法后，系统辨识误差基本趋于零，而(b)图的误差明显较大。图7中，(a)为本文提出的方法的轨迹跟踪图，y为系统实际输出，yd为期望输出， (b)为传统控制方法的轨迹跟踪图，经历一段时间后，(a)系统输出与期望轨迹基本重合。图8(a)为本文所提方法的轨迹跟踪误差曲线图，(b)为传统控制方法的轨迹跟踪误差曲线图，由图可知：(a)中跟踪误差曲线在约6 s后稳定到零，(b)显示的误差较大，从而证明了本文方法的优越性和可行性。

图8　轨迹跟踪误差曲线

6结束语

本文结合模糊神经网络，设计了滑模控制器跟踪控制具有死区输入的非线性不确定混沌系统。为提高模糊神经网络的识别性能，本文引入粒子群优化算法选取最优解，从而使识别误差达到最小，利用李雅普诺夫稳定性理论，证明该系统的稳定性。本文的独特之处在于考虑了死区输入，并利用基于粒子群算法的模糊神经网络对不确定混沌系统进行辨识。仿真结果表明：该方法的辨识误差和跟踪误差较小，但其误差收敛速率有待提高。下一步的研究内容包括对模糊神经网络的网络结构和参数同时进行优化，从而使辨识误差进一步降低，提高误差收敛速率，进而优化滑模控制器的跟踪性能。

参考文献：

[1]LIN D,LIU H J,SONG H.Fuzzy neural control of uncertain chaotic systems with backlash nonlinearity[J].International Journal of Machine Learning and Cybernetics,2014,5(5):721-728.

[2]廖晓峰,肖迪,陈勇，等.混沌密码学原理及其应用[M].北京:科学出版社,2009.

[3]TAO G,KOKOTOVIC P V.Adaptive sliding control of plants with unknown dead-zone[J].IEEE Trans.Autom.Control,1994,39(1):59-68.

[4]HER-TERNG Y.Generalized projective chaos synchronization of gyroscope systems subjected to dead-zone nonlinear inputs[J].Physics Letters A,2008,372(14):2380-2385.

[5]李敏,王家序,肖科,等.模糊逻辑及神经网络动态摩擦和死区补偿的机器人滑模变控制[J].重庆大学学报,2013(6):18-25.

[6]ZHANG T P,SHUZHI SAM GE.Adaptive Neural Network Tracking Control of MIMO Nonlinear Systems With Unknown Dead Zones and Control Directions[J].IEEE Trans.Actions on neural networks,2009,20(3):3-15.

[7]ZHOU J,WEN C Y,ZHANG Y.Adaptive output control of nonlinear systems with uncertain dead-zone nonlinearity[J].IEEE Trans.Autom.Control,2006,51(3):504-511.

[8]葛维维,张天平.带有未知死区的机器人积分变结构模糊控制[J].电光与控制,2011(6):31-36.

[9]ALIEV R A,FAZLOLLAHI B,VAHIDOV R M.Genetic algorithmbased learning of fuzzy neural networks.Part I:Feed-forward fuzzy neural networks[J].Fuzzy Sets Syst,2001,118(3):351-358.

[10]李研,毛志忠,王琰.自适应动态径向基函数网络死区补偿控制[J].控制理论与应用,2009(12):1395-1400.

[11]GAO Y,JOO ER MENG.Online Adaptive Fuzzy Neural Identification and Control of a Class of MIMO Nonlinear Systems[J].IEEE Transactions on fuzzy systems,2003,11.

[12]SELMIC R R,LEWIS F L.Deadzone compensation in motion control systems using neural networks[J].IEEE Trans.Autom.Control,2000,45(4):602-613.

[13]WANG X S,HONG H,SU C Y.Model reference adaptive control of continuous time systems with an unknown dead-zone[J].Inst.Electr.Eng.Proc-Control Theory Appl,2003,150(3):261-266.

[14]姚毅,陈光建,贾金玲.基于模糊神经网络算法的机器人路径规划研究[J].四川理工学院学报(自然科学版),2014(6):30-33.

[15]KALPANA M,BALASUBRAMANIAM P,RATNAVELU K.Direct delay decomposition approach to synchronization of chaotic fuzzy cellular neural networks with discrete unbounded distributed delays and Markovian jumping parameters[J].Applied Mathematics and Computation,2015,254:291-304.

[16]SONG Y,CHEN Z Q,YUAN Z Z.New Chaotic PSO-Based Neural Network Predictive Control for Nonlinear Predictive[J].IEEE Transactions on neural networks,2007,18(2)：595-600..

(责任编辑杨黎丽)

Uncertain Chaotic Systems Control with Dead-Zone Input

XIE Yu-jiao, LIN Da, BIAN Xiao-jun

(School of Automation and Electronic Information,Sichuan University of Science & Engineering, Zigong 643000, China)

Abstract:Most industrial control systems exist Dead-zone input which has great influence on the performance of the control system. This paper used the approximation ability of Fuzzy neural network to identify the Chaos system with uncertainty and Dead zone. Further more, it can adaptively compensate for its non smooth and nonlinear characteristics. In order to improve the performance of the fuzzy neural network and abtain the minimum identification error, the parameters of fuzzy neural network were optimized by particle swarm optimization algorithm. In the control part of the system, this paper introduced the sliding mode control to track the input signals. At the end of this paper, the feasibility and superiority of the proposed method were demonstrated by the simulation of Duffing system.

Key words:dead zone input; fuzzy neural network; particle swarm optimization algorithm; sliding-mode control

文章编号：1674-8425(2016)04-0120-07

中图分类号：TP183

文献标识码：A

doi:10.3969/j.issn.1674-8425(z).2016.04.021

作者简介：谢玉姣(1990—)，女，江苏徐州人,硕士研究生,主要从事智能控制方向的研究；林达(1974—)，男，山东日照人,副教授,博士,主要从事混沌控制方向的研究。

基金项目：四川省省属高校科研创新团队项目 (TD15024)

收稿日期：2015-07-13

引用格式：谢玉姣，林达，边潇俊.具有死区输入的不确定混沌系统控制[J].重庆理工大学学报(自然科学)，2016(4):120-126.

Citation format：XIE Yu-jiao, LIN Da, BIAN Xiao-jun.Uncertain Chaotic Systems Control with Dead-Zone Input[J].Journal of Chongqing University of Technology(Natural Science)，2016(4):120-126.