阻尼对车身高度控制效果的影响分析

李仲兴,于文浩

(江苏大学 汽车与交通工程学院，江苏 镇江　212013)



阻尼对车身高度控制效果的影响分析

李仲兴,于文浩

(江苏大学 汽车与交通工程学院，江苏 镇江212013)

摘要：随着阻尼可变半主动悬架应用的日益广泛，不考虑阻尼变化因素的传统车身高度控制策略已不能很好地满足控制要求。为探索阻尼对车身高度控制的影响，研究了不同阻尼状态下车身高度阶跃激励响应，并对比了在不同阻尼状态下相同PID参数的控制效果。结果表明：当阻尼系数发生变化后，车身高度调节过程产生一定的波动，原有的PID控制参数不再满足系统的控制要求。为此，利用遗传算法对不同阻尼状态下的车身高度控制策略PID参数进行了整定。结果表明：随阻尼系数增大，比例系数Kp和微分系数Kd应适度增加。

关键词：车身；电控空气悬架；高度控制；阻尼；遗传算法

车身高度可调的空气悬架能够实现对车身高度的主动控制，具有良好的行驶平顺性和行驶安全性。国内外诸多学者对其控制理论进行了大量研究，提出了模糊PID控制法、滑动模态法、变速积分PID控制法等控制策略[1-4]。随着阻尼可变的半主动悬架应用日益广泛，一些学者也对车身高度与阻尼的集成控制进行了探索。

2012年，汪若尘[5]建立了车身高度与可调阻尼的集成控制系统，并通过试验验证了其控制策略的有效性，但其仿真和试验结果中未涉及车身高度在实车运行时发生变动的情况，阻尼变化对车身高度调节的影响不得而知。2015年，汽车仿真与控制国家重点实验室的赵景波[6]提出一种主动悬架系统高度与阻尼集成控制方法，并通过试验验证了不同车身高度和不同阻尼形式的组合对车辆性能的影响，但试验未涉及车身高度调节的动态过程，未能凸显阻尼变动对车身高度的调节。

随着阻尼可变的半主动悬架应用日益广泛，传统的不考虑阻尼变化因素的车身高度控制策略已不能很好地满足控制系统的要求。为提高在不同阻尼状态下的车身高度控制效果，提升车身高度与阻尼集成控制系统的动态性能，深入分析阻尼状态对车身高度控制效果的影响，研究理想的车身高度控制参数随阻尼状态的变化规律就具有较高的理论意义和一定的工程应用价值。

1空气悬架高度调节的数学模型

由于高度调节是在空气弹簧工作点附近，因此通过泰勒级数展开略去高阶项对模型进行线性化处理。在充气过程中管路主要对气体流量衰减和系统响应延迟产生影响，但由于充气速度非常快，所以管路延迟很小，因此在理论计算中可将管路流量衰减用流量衰减系数表示。流经管路后的气体质量流量为

(1)

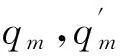
由式(1)结合空气悬架动力学模型和变质量开口系统充放气模型可得

(2)

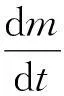
将式(1)通过拉氏变换可得车身高度对质量流量的传递函数：

(3)

式中：X(s)为拉氏变换后的空气弹簧变形量；Qm(s)为拉式变换后的空气弹簧流进或流出的气体质量流量。

该传递函数已在文献[4]中得到试验验证。传递函数包括积分环节、2阶震荡环节和延滞环节。显然，阻尼系数Cs变化会影响到2阶震荡环节的阻尼比ξ，而阻尼比ξ会随着阻尼系数Cs的增大而增大。

2阻尼状态对车身高度调节的影响

2.1不同阻尼状态下车身高度阶跃响应

结合以上车身高度调节传递函数，在 Matlab/Simulink环境下进行仿真，以模拟车身高度调节。在实际操作过程中车身高度调节是在多种车身高度间切换，车身高度的增加和降低并不能左右阻尼状态对车身高度调节的影响，因此本文仅取车身高度增加的一种情况来模拟，以探究阻尼对车身高度调节过程的影响。

通过对车身高度调节模型施加0.01 kg/s的质量流量作为系统阶跃激励，探究不同阻尼系数下的车身高度调节阶跃响应特性。表1为仿真主要参数[7]。

由于车身高度调节传递函数拥有1阶积分环节，因此整个系统的阶跃响应近似其2阶震荡环节的斜坡响应。由于在激励初始，各极点对应的瞬态分量尚未衰减到稳态[8]，因此更容易看出传递函数中系数变化对系统的影响。选取阻尼系数Cs分别为4 000，9 000和14 000 N·(s·m-1)时阶跃激励下车身高度前1 s的响应结果进行分析，如图1所示。

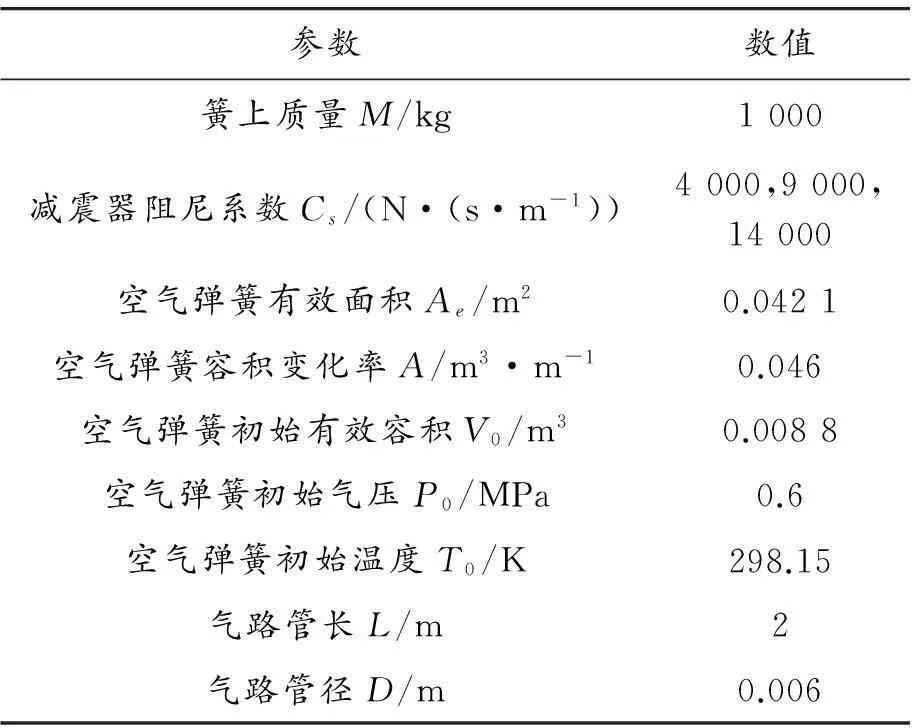
表1　仿真主要参数

图1　车身高度调节阶跃响应

从仿真结果可以看出:系统响应除拥有延滞系统的阶跃响应特性外，还随阻尼系数减小产生了幅值逐渐增大的波动。

2.2不同阻尼状态下车身高度PID控制结果

选取阻尼系数Cs为9 000 N·(s·m-1)的车身高度调节系统进行PID控制参数整定，探究当阻尼系数发生变化时，针对某一固定阻尼系数值整定的PID控制参数是否依旧能适应新系统的控制要求。车身高度控制策略如图2所示。

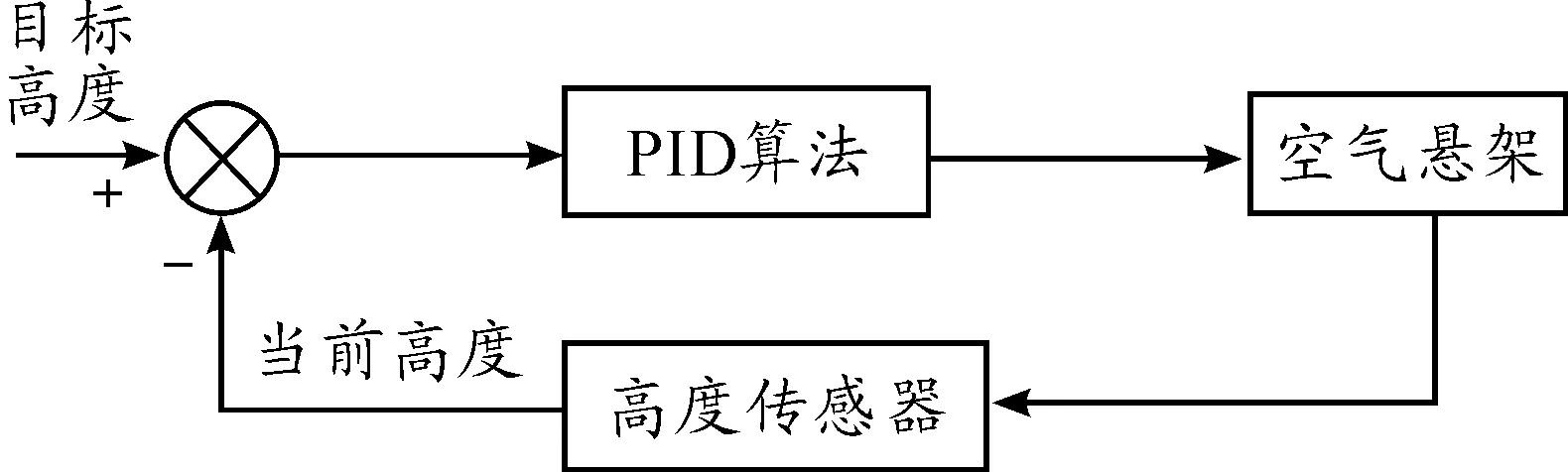
图2　车身高度控制策略

为方便建模及计算，在PID算法中将积分时间常数Ti的倒数和微分时间常数Td分别表示为积分系数Ki和微分系数Kd。表2为当阻尼系数Cs为9 000 N·(s·m-1)时车身高度调节系统整定的PID控制参数和车身高度调节目标高度。

表2　PID控制仿真参数

从仿真结果图3可以看出:在阻尼系数Cs为 4 000 N·(s·m-1)时，车身高度调节过程出现了明显的波动，同时调节时间也有所增加，车身高度调节品质较差；在阻尼系数Cs为14 000 N·(s·m-1)时，车身高度调节过程十分平稳，调节时间基本不变，但同时也表明对于高阻尼系数的车身高度调节该组PID控制参数过于保守，使得系统调节缓慢、效率低下。因此，针对某一阻尼系数进行优化整定的PID控制参数并不能很好地满足车身高度调节的控制需求。

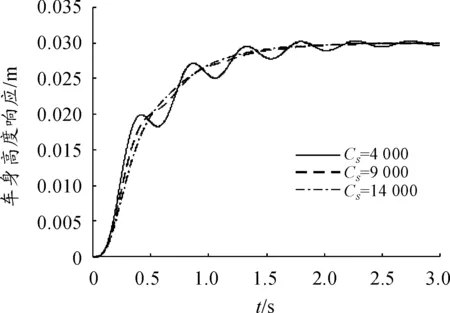
图3　不同阻尼系数下车身高度调节PID控制过程

3不同阻尼状态下PID控制参数探究

3.1应用改进遗传算法的PID控制参数寻优

遗传算法GA(genetic algorithms,GA)是模拟生物在自然环境中的遗传和进化过程而形成的一种全局优化概率搜索算法。遗传算法无需对目标函数微分，可提高参数优化水平，简化优化的解析计算过程[9]。因此，在本文建立的仿真模型的基础上使用江苏大学刘虹[10]提出的采用最优保存策略和自适应策略改进的遗传算法进行车身高度PID控制参数寻优，既可以确保遗传算法的全局收敛性，又能避免搜索停滞不前和早熟现象的发生。

传统基于遗传算法的PID参数整定一般将误差积分指标作为系统整定的性能指标[11]。根据图3的结果可知：车身高度PID控制还应抑制控制过程中的超调和震荡现象。然而以上的性能指标对于控制过程中的超调和震荡均缺乏有效的评判能力，因此在传统的绝对误差积分的基础上加入超调和震荡作为车身高度PID控制系统整定的性能指标。其中：超调指标为系统超调时的绝对误差对时间的积分值；震荡指标为车身高度与高度变化趋势相反时的绝对误差对时间的积分值。同时，由于在车身高度PID控制过程中调节时间和误差与超调量存在一定的制约关系，因此，还需要分别给予一定的权重进行相应的妥协。根据以上要求制定车身高度PID控制的遗传算法寻优目标参数：

(4)

其中：J为目标函数值；tu为调节时间；E(t)为调节过程的绝对误差对时间的积分值；a为权重系数，根据Mp(t)+S(t)与E(t)数量级的差异，此处a取100；Mp(t)为超调指标；S(t)为震荡指标；t为仿真时间。

3.2不同阻尼状态下PID控制参数的寻优结果

遗传算法其他参数设置为：种群大小M=60；采用二进制编码，编码长度为10；遗传代数为500；交叉概率pc=0.6；变异概率pm=0.01；经过初步试验取Kp=0～50，Ki=0～10，Kd=0～30；阻尼系数Cs= 4 000～14 000 N·(s·m-1)。参数整定后的PID控制参数中积分系数Ki恒为0，微分系数为一个较小且不为0的数，并有随阻尼系数Cs增大而增大的趋势。比例系数Kp的结果及其2阶拟合曲线如图4所示。从图中可以看出：当阻尼系数Cs从4 000 N·(s·m-1)逐渐增大时，比例系数Kp先增大而后逐渐趋于平稳。

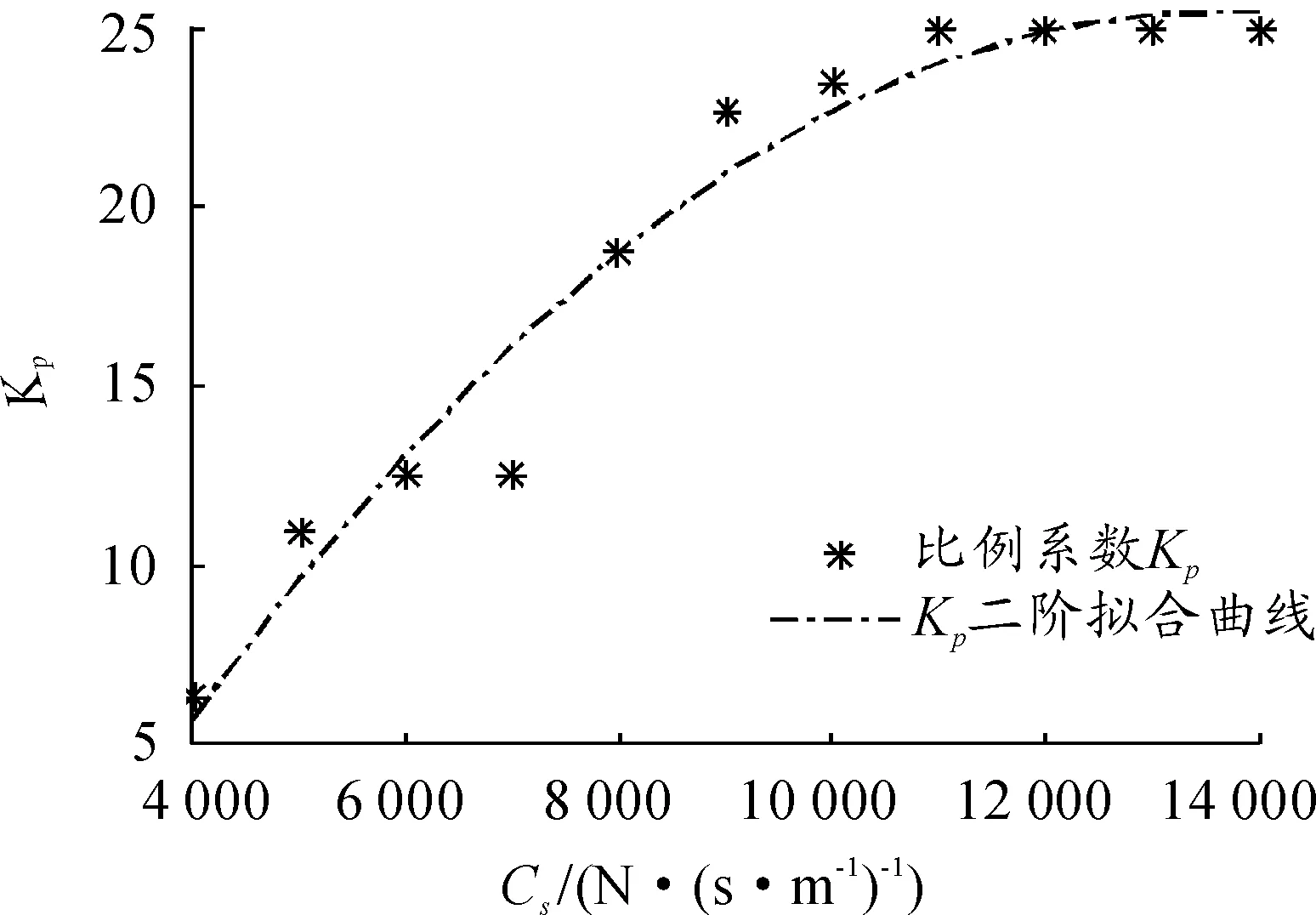
图4　整定后的车身高度调节比例系数Kp值

3.3PID控制参数优化结果的原因探讨

随着阻尼系数的增大，车身高度调节的传递函数中2阶震荡环节阻尼比ξ增大，使得系统能更快达到稳态，因此，可以在保证调节过程中出现较少的震荡和超调的情况下在一定程度上增大比例系数Kp的值，使得系统调节时间更短。但在车身高度调节中，阻尼比ξ变化只能引起传递函数幅值裕量的微小改变，因此，为保证系统稳定，比例系数Kp的值并不能无限制地增大。若比例系数Kp继续增大将会引起系统的振荡，使得调节品质变差，这也是寻优结果中比例系数Kp最终不再持续增大的原因。

在车身高度调节的传递函数中有一个纯积分环节。若积分系数Ki不为0，则意味着系统中拥有一个2阶纯积分环节。此环节为非稳定环节，会大幅增加整个车身高度调节系统的超调量和震荡程度，因此将积分系数Ki置0可以在有效进行车身高度控制的同时消除系统超调震荡以改善车身高度控制性能[12]。

PID控制参数中微分系数Kd增大会使车身高度调节系统的调节时间增加，同时导致调节过程出现一定程度的波动。为消除波动，应减小比例系数Kd的值，从而使得系统调节过程平稳，但调节时间大幅增加。因此，在对调节过程平稳要求不是非常高的情况下，遗传算法的寻优结果将更偏向于取较小的微分系数Kd和较大的比例系数Kp。

在一般情况下，仅运用比例控制即可在容忍调节过程微小波动的情况下对车身高度调节进行较好的控制，且比例系数Kp随阻尼系数的增大而增大。若追求调节过程的平稳，选取一组合适的比例和微分控制参数即可获得更加平稳的车身高度调节过程，但需要较长的调节时间，且微分系数Kd和比例系数Kp都将随阻尼系数的增大而增大。

4结束语

根据现有的车身高度调节数学模型，对其施加阶跃激励，分析了不同的阻尼系数对车身高度阶跃激励响应特性的影响。同时利用一组PID控制参数得出：当阻尼系数发生变化后，针对原阻尼系数整定的PID控制参数在调整过程中有震荡和超调等情况发生，不再满足系统的控制要求。

在传统遗传算法PID参数整定性能指标的基础上制定了适用于车身高度调节的目标函数，并对在阻尼系数依次变化下的车身高度调节系统进行PID参数寻优。结果表明：在不影响系统稳定性的前提下比例系数Kp应随阻尼系数的增大而增大，同时合理匹配微分系数Kd，可以在调节时间与调节过程平稳间进行一定的侧重。

积分系数Ki置0即可使车身高度调节拥有更好的时域响应结果，这是由于车身高度在质量流量的传递函数中已具备积分环节，若再引入一个积分环节则使得系统拥有一个非稳定的2阶积分环节，这将增大系统控制难度，从而降低系统的调节品质。

参考文献：

[1]何二宝,杜群贵,冯元元.电控空气悬架车身高度调节的模糊PID控制[J].机床与液压,2012,40(5):86-88.

[2]陈月霞,陈龙,黄晨.ECAS车辆车身高度调节系统与整车性能匹配研究[J].振动、测试与诊断,2013,33(1):73-76.

[3]KIMH,LEEH.HeightandLevelingControlofAutomotiveAirSuspensionSystemUsingSlidingModeApproach[J].TRANSACTIONSONVEHICULARTECHNOLOGY,2011,60(5):2027-2041.

[4]窦辉,陈龙,汪少华.电控闭式空气悬架车高调节控制研究[J].机械设计与制造，2014(9):171-174.

[5]汪若尘,张孝良,陈龙.车身高度与可调阻尼集成控制系统[J].农业工程学报,2012,28(11):75-79.

[6]赵景波,倪彰,贝绍轶.电动化底盘主动悬架系统高度与阻尼集成控制[J].广西大学学报,2015,40(2)：347-356.

[7]徐兴,陈照章,李仲兴.ECAS客车车身高度调节建模机器控制研究[J].汽车技术,2009 (11)：42-46.

[8]王显正,莫锦秋,王旭永.控制理论基础[M].北京:科学出版社,2010:204-205.

[9]毛敏,于希宁.基于遗传算法的PID参数优化方法[J].中国电力,2002,35(8)：48-51.

[10]刘虹.应用改进遗传算法进行PID控制器参数整定[D].镇江:江苏大学,2006:1-6.

[11]王琛,王仕成.基于遗传算法的PID参数整定及仿真[J].计算机仿真,2005,22(10)：112-143.

[12]宋宇.空气悬架车辆车身高度PID控制的仿真研究[J].湖北汽车工业学院学报,2007,21(2):1-4.

(责任编辑刘舸)

Influence Analysis of Damping on Body Height Control Effect

LI Zhong-xing, YU Wen-hao

(School of Automotive and Traffic Engineering, Jiangsu University, Zhenjiang 212013, China)

Abstract:With the increasing application of damping variable semi-active suspension, the traditional vehicle body height control strategy which is without consideration of damping factor can’t meet the requirement of control. In order to explore the effect of damping on vehicle body height control, the step responses of the body height on different damping states were comparatively studied; and compared with the control effect results of the same PID control parameters on different damping states, the results show that the damping has obvious influence on the body height adjustment process, and when the damping is changed, the same PID control parameters can no longer meet the requirements of the control system. Therefore we used the genetic algorithm to tunn the PID parameters of the body height control strategy under different damping states, and the results show that, with the increase of damping coefficient, the proportional coefficient Kp and differential coefficient Kd should be moderately increased.

Key words:body; electrically controlled air suspension; height control; damping; genetic algorithm

文章编号：1674-8425(2016)04-0011-05

中图分类号：U463.33+4.2

文献标识码：A

doi:10.3969/j.issn.1674-8425(z).2016.04.003

作者简介：李仲兴(1963—)，男，上海人，博士，教授，博士生导师，主要从事车辆动态性能模拟与控制研究。

收稿日期：2015-10-25

引用格式：李仲兴,于文浩.阻尼对车身高度控制效果的影响分析[J].重庆理工大学学报(自然科学)，2016(4):11-15.

Citation format：LI Zhong-xing, YU Wen-hao.Influence Analysis of Damping on Body Height Control Effect[J].Journal of Chongqing University of Technology(Natural Science)，2016(4):11-15.