惟一强*-clean 环

王秀兰，李春娜

(1.天津农学院基础科学学院，天津 300384；2.浙江工业大学之江学院理学院，浙江 杭州 310024)



惟一强*-clean 环

王秀兰1，李春娜2

(1.天津农学院基础科学学院，天津 300384；2.浙江工业大学之江学院理学院，浙江 杭州 310024)

摘要：*-环R被称为惟一强*-clean环，如果R中每个元素都可以惟一表示成可交换的单位和投射的和.本文中给出一个*-环是惟一强*-clean环的等价条件并给出几个惟一强*-clean环的例子.

关键词：惟一*-exchange环；强*-clean环；惟一强*-clean环

0引言

本文中，R是一个有单位元1的结合环.称R为(惟一)clean环，如果R中每个元素都可以(惟一)表示成幂等元和单位的和.称R为(惟一)强clean环，如果R中每个元素都可以(惟一)表示成可交换的幂等元和单位的和.(惟一)clean环和(惟一)强clean环与正则环、强π正则环以及布尔环等环类有着密切联系，可参考文献[1-5].

环R上的对合作用*(*：R→R)是一个反自同构，即对任意的x,y∈R有(x+y)*=x*+y*,(xy)*=y*x*和(x*)*=x.一个有*作用的环称之为*-环.如果*-环R中的元素e满足e2=e=e*,则称元素e是一个投射.显然，0和1是任意一个*-环的投射.文献[6]中在clean环和强clean环中引入了*-作用，称一个*-环R为*-clean环，如果R中每个元素都可以表示成投射和单位的和；称一个*-环R为强*-clean环，如果R中每个元素都可以表示成可交换的投射和单位的和.受此启发，称R为惟一*-clean环，如果R中每个元素都可以惟一表示成投射和单位的和；称R为惟一强*-clean环，如果R中每个元素都可以惟一表示成可交换的投射和单位的和.显然，惟一强*-clean环是强*-clean环.本文研究惟一强*-clean环，给出惟一强*-clean环的几个等价条件并且构造几个惟一强*-clean环的例子.记号U(R),J(R)分别表示由R的单位组成的集合和R的雅各布森根，Cn表示n阶循环群，Zn表示整数模n的剩余类环.

1惟一强*-clean环

文献[7]中，定义了(左，右)惟一exchange环.类似地，可以定义(左，右)惟一*-exchange环.

定义1.1如果对于*-环R中任意的a∈R,存在惟一投射e使得e∈Ra和1-e∈R(1-a)成立，则称R为左惟一*-exchange环；如果对于*-环R中任意的a∈R,存在惟一投射e使得e∈aR和1-e∈(1-a)R成立，则称R为右惟一*-exchange环；如果R既是左惟一*-exchange环又是右惟一*-exchange环，则称R为惟一*-exchange环.

如果R中每个幂等元是中心的，则称R是abelian； 如果*-环R中每个投射是中心的，则称R是*-abelian.

引理1.1[8,引理2.1]如果*-环R中每个幂等元是投射，则R是*-abelian.

定理1.1对于*-环R，下列条件等价：

(1)R是左惟一*-exchange环；

(2)R是左惟一exchange环且R中每个幂等元是投射；

(3)R是惟一强clean环且R中每个幂等元是投射；

(4)R是惟一clean环且R中每个幂等元是投射；

(5)R是abelian惟一*-clean环；

(6)R是惟一*-clean环且对任意投射a∈R和任意u∈U(R)，ueu-1也是投射；

(7)R是惟一强*-clean环.

定理1.1的证明(1)→(2).若R是一个左惟一*-exchange环，根据定义1.1，对任意的a2-a∈R,存在一个投射e使得e∈Ra和1-e∈R(1-a)成立，即存在某个x∈R和某个y∈R使得e=xa和1-e=y(1-a)成立.因此，e=xa=xa2=ea且1-e=y(1-a)=y(1-a)2=(1-e)(1-a).从而得到a=e是一个投射，即R中每个幂等元是投射.此外，R也是左惟一exchange环.

(2)⟹(3).由文献[7,命题2.2.7]，左惟一exchange环是惟一强clean 环.

(3)⟹(4).若R中每个幂等元是投射，由引理1.1，R中每个幂等元(投射)是中心的.根据文献[2，例4]，R是惟一clean环.

(4)⟹(5)、(5)⟹(6)和(5)⟹(7),显然.

(7)⟹(3).因为R是惟一强*-clean环，所以R是强*-clean环.根据文献[8,定理2.2]，R中每个幂等元是投射且R是惟一强clean环.

(6)⟹(4).任取e2=e∈R，由(6)知e=f+u，其中f2=f+f*,u∈R.显然f+u=(f+u)2=f+u2+fu+uf，即u=u2+fu+uf，故1=u+f+ufu-1.根据(6)，显然e=f+u=1-ufu-1=u(1-f)u-1是一个投射，即R中每个幂等元是投射.R是惟一*-clean环，从而也是惟一clean环.

(4)⟹(1).根据文献[7,推论2.1.10]，惟一clean环是左惟一exchange环，(1)显然成立.

定理1.1中，条件(5)可由下列条件替换：R是*-abelian惟一*-clean环；条件(1)中“左惟一*-exchange环”可由“右惟一*-exchange环”替换且条件(2)中“左惟一exchange环”由“右惟一exchange环”替换.从而有下面推论1.1：

推论1.1对于*-环R，下列叙述等价：

(1)R是左惟一*-exchange环；

(2)R是右惟一*-exchange环；

(3)R是惟一*-exchange环；

(4)R是惟一强*-clean环；

(5)R是*-abelian惟一*-clean环.

下面给出惟一强*-clean环结构的刻画，首先给出下面引理1.2.

引理1.2若R/J(R)是布尔环，则对任意u1,u2∈U(R)有u1-u2∈J(R).

令R是一个*-环，I是R的*-理想(即I=I*)，如果对任意a2-a∈I和a*-a∈I，存在(惟一)投射e∈I使得e-a∈I,则称投射模I可(惟一)提升.

*-环R被称为*-布尔环，如果R中每个元素是投射.显然，如果R是*-布尔环，则*=1R.实际上，如果R是*-环，则R是*-布尔环与R是布尔环等价.

定理1.2对于*-环R，下列叙述等价：

(1)R是惟一强*-clean环；

(2)R/J(R)是布尔环，投射模J(R)可提升且R中的投射是中心的；

(3) 对任意a∈R，存在中心投射e∈R使得e-a∈J(R).

定理1.2的证明(1)⟹(2).假设R是惟一强*-clean环，由定理1.1，R是惟一clean环且R中每个幂等元是投射，再由引理1.1，R中每个投射是中心的.从而由文献[5，定理20]，R/J(R)是布尔环，幂等元(也是投射)模J(R)可提升.

(2)⟹(3).对任意a∈R，由(2)，存在中心投射e∈R使得e-a∈J(R).

(3)⟹(1).对任意a∈R，存在中心投射e∈R使得e-(a-1)∈J(R).令ω=(a-1)-e∈J(R),则a=e+(ω+1),其中e2=e=e*,(ω+1)∈U(R)且e(ω+1)=(ω+1)e.这就证明了R是强*-clean环,下面证明惟一性.如果还有表达式a=f+u，其中f2=f=f*.u∈U(R)且fu=uf，由引理1.2，e-f=u-(ω+1)∈J(R).在e-f∈J(R)左侧乘以e，得到e(e-f)=e-ef=e(1-f)∈J(R)是一个幂等元.因为J(R)中的幂等元只有0，故e=ef.同理，f=fe.因为投射e是中心的，所以e=f.

例1.1R是局部*-环，则下列叙述等价：

(1)R是惟一强*-clean环；

(2)R/J(R)≅Z2;

(3)R是惟一*-clean环；

(4)R是惟一clean环.

定义1.2如果*-环R中的每个元素都可以惟一表示成一个投射和J(R)中元素的和，则称R为惟一J-*-clean 环.

由惟一J-*-clean 环的定义，不难得到下面的结论：

定理1.3对于*-环R，下列叙述等价：

(1)R是惟一J-*-clean 环；

(2)R/J(R)是布尔环，投射模J(R)可提升；

(3) 对任意a∈R，存在惟一一个投射e∈R使得e-a∈J(R).

定理1.4如果*-环R是惟一J-*-clean 环，则R是惟一*-clean 环.

定理1.4的证明由定理1.3，对任意a∈R，存在惟一一个投射e∈R使得ω=(a-1)-e∈J(R),即a=e+(ω+1)，其中e2=e=e*,(ω+1)∈U(R)，从而R是惟一*-clean 环.

定理1.5如果*-环R是惟一强*-clean 环，则R是惟一J-*-clean 环.

定理1.5的证明由定理1.2，对任意a∈R，存在一个中心投射e∈R使得e-a∈J(R).根据定理1.3，只需要证明投射e的惟一性.假设存在另外一个投射f∈R使得f-a∈J(R)，则e-f∈J(R).在e-f∈J(R)左侧乘以e，得到e(e-f)=e(1-f)∈J(R)是一个幂等元,故e=ef.同理，f=fe.因为投射e是中心的，所以e=f.

若R是*-环，则由定理1.1、定理1.4和定理1.5得到如下关系：

R是惟一强*-clean 环⟺R是(左、右)惟一*-exchange环⟺R是惟一J-*-clean 环⟺R是惟一*-clean 环⟺R是强*-clean 环，但是，反之是否成立？

问题：(1) 如果R是惟一*-clean 环，是否有2∈J(R)？

(2) 如果R是惟一*-clean 环，投射模J(R)是否可(惟一)提升？

2惟一强*-clean环的扩张

如果加法abelian群R⊕R有乘法运算(a,b)(c,d)=(ac,ad+bc)，则称为环R的平凡扩张R∝R.

例2.1(1) 若R是一个*-环,定义环R∝R上的*-运算，仍记为*，满足(a,b)*=(a*,b*)，则R是惟一强*-clean 环当且仅当R∝R是惟一强*-clean 环.

(2) 若R是一个*-环,定义环R∝R上的*-运算，仍记为*，满足(a,b)*=(a*,-b*)，则R是惟一强*-clean 环当且仅当R∝R是惟一强*-clean 环.

例2.1的证明：(1) 由文献[8，例2.4]，只需要证明惟一性.假设R是惟一强*-clean 环，因为R∝R中的每个投射是(e,0)这种形式，其中e2=e=e*∈R,而R∝R中的每个单位是(u,c)这种形式，其中u∈U(R).从而对于任意(a,b)∈R∝R,(a,b)=(e,0)+(u,c).显然，a=e+u是a在R中的强*-clean表示.由于R是惟一强*-clean 环，所以e由a惟一确定，从而(e,0)由(a,b)惟一确定.反之，假设R∝R是惟一强*-clean 环，则对任意a∈R有(a,0)=(e,0)+(u,0)，其中e2=e=e*∈R,u∈U(R).由于R∝R是惟一强*-clean 环，所以(e,0)由(a,b)惟一确定,从而e由a惟一确定.因此，a=e+u是a在R中的惟一强*-clean表示.

(2) 证明过程和(1)类似.

定理2.1惟一强*-clean 环的商环是惟一强*-clean 环.

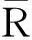
推论2.1如果R是惟一强*-clean 环，e是R的投射，则eRe是惟一强*-clean 环.

推论2.1的证明由于eRe同构于与R的一个商环，根据定理2.1，结论成立.

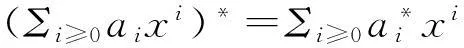
定理2.2令R是一个*-环,R是惟一强*-clean 环当且仅当R[[x]]是惟一强*-clean 环.

定理2.2的证明⟹由文献[8，推论2.10]，R[[x]]是强*-clean 环.下面只需要证明惟一性.任取α∈R[[x]]且α=e+β，其中e2=e=e*∈R[[x]]，β∈U(R[[x]]).因为R是abelian，所以e∈R.令I(α),I(β)分别表示α和β的常数部分，则I(α)=e+I(β)且I(α),I(β)∈R，显然I(β)∈U(R).因此式子I(α)=e+I(β)是I(α)在R中的强*-clean表示.又因为R是惟一强*-clean 环，所以e由I(α)惟一确定，从而由α惟一确定.

⟸由文献[8，推论2.10]，R是强*-clean 环.因此，R是abelian且R[[x]]中每个幂等元包含在R中.令α∈R，则α=e+β,其中e2=e=e*∈R，β∈U(R[[x]])，显然β=a-e∈U(R).由于e由a惟一确定,所以a=e+β是α在R中的惟一强*-clean 表示.

3惟一强*-clean群环

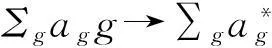
定理3.1若R是*-环,G是局部有限群，则RG是惟一强*-clean群环当且仅当R是惟一强*-clean 环且G是2-群.

定理3.1的证明⟹RG是惟一强*-clean 群环，由定理1.1，RG是惟一clean环且RG中每个幂等元都是投射.又由文献[9,定理12]，R是惟一clean 环，G是2-群且RG中的幂等元都在R中.因为RG中每个幂等元都是投射，所以R中每个幂等元也是投射.再由定理1.1，R是惟一强*-clean 环.

⟸R是惟一强*-clean 环，由定理1.1，R是惟一clean环且R中每个幂等元是投射.根据文献[2,例4]，R是惟一强clean 环.由文献[2,引理16]知2∈J(R)，又因G是一个2-群，故由文献[9,定理12]得RG是惟一clean环.根据文献[5,引理4]，R中每个幂等元是中心的，而2∈J(R)，由文献[9,引理11]，RG中的幂等元都包含在R中.所以，RG中的每个幂等元都是投射，从而再由定理1.1可得RG是惟一强*-clean 群环.

推论3.1若R是*-环,G是一个局部有限群，则RG是惟一强*-exchange群环当且仅当R是惟一强*-exchange环且G是2-群.

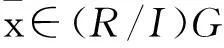
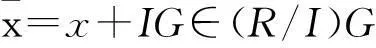
显然，不包含任意非平凡中心投射的强*-clean环是局部环.

定理3.2令G是一个群，S是任意的局部*-环.若SG是强*-clean群环，则对任意的强*-clean环R，RG是强*-clean群环.

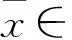
定理3.3若R是一个局部*-环,G是一个abelian初等2-群，则RG是强*-clean群环.

定理3.3的证明由于G是一个abelian初等2-群，不妨假定G是一个有限群，从而G是n个循环群C2的直和(n≥1).若2∈U(R)，RC2≅R⊕R.记R(C2×C2)≅RC2⊕RC2≅R⊕R⊕R⊕R，则RG≅⊕2nR是强*-clean群环.若2∈J(R)，由文献[8，推论2.13]，RG是强*-clean群环.

推论3.2若R是一个强*-clean环，G是一个abelian初等2-群,则RG是强*-clean群环.

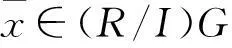
推论3.2中，G是abelian初等2-群不是必要条件，如下面例3.1：

例3.1令R=Z2={0,1},G=C3={1,g,g2}且*=1R，则RG是强*-clean群环.实际上，

RG={0,1,g,g2,1+g,1+g2,g+g2,1+g+g2},

P(RG)={0,1,g+g2.1+g+g2},

U(RG)={0,1,g,g2},

显然，Z2C3中的每个元素是强*-clean元，但是1+g=(1+g+g2)+g2,1+g2=(1+g+g2)+g不是惟一强*-clean群环.

例3.1也给出了强*-clean 环但不是惟一强*-clean环的一个例子.

4参考文献

[1] Anderson D D,Camillo V P.Commutative rings whose elements are a sum of a unit and idempotent[J].Comm Alg,2002,30(7):3327-3336.

[2] Chen J,Wang Z,Zhou Y.Rings in which elements are uniquely the sum of an idempotent and a unit that commute[J].J Pure Appl Alg,2009,213:215-223.

[3] Nicholson W K.Liftingidempotents and exchange rings[J].Trans AMS,1977,229:269-278.

[4] Nicholson W K.Strongly clean rings and Fitting's Lemma[J].Comm Alg,1999,27:3583-3592.

[5] Nicholson W K,Zhou Y.Rings in which elements are uniquely the sum of an idempotent and a unit[J].Glasg Math J,2004,46:227-236.

[6] Vaš L.*-Clean rings; some clean and almost clean Baer *-rings and von Neumann algebras[J].J Algebra,2010,324:3388-3400.

[7] 应志领.Clean环和正则局部环[D].南京:东南大学,2009:9-16.

[8] Li C,Zhou Y.On strongly *-clean rings[J].J Alg Appl,2011,10(6):1363-1370.

[9] Chen J,Nicholson W K,Zhou Y.Group rings in which every element is uniquely the sum of a unit and an idempotent[J].J Algebra,2006,306:453-460.

(责任编辑赵燕)

Uniquely strongly *-clean rings

WANG Xiulan1，LI Chunna2

(1.School of Basic Science，Tianjin Agricultural University，Tianjin 300384，China；2.College of Science，Zhijiang College of Zhejiang University of Technology，Hangzhou 310024，China)

Abstract:A *-ring R is uniquely strongly *-clean if every element of R is uniquely the sum of a unit and a projection that commute with each other.In this article,we study the equivalent conditions of a *-ring being uniquely strongly *-clean.Moreover,some examples of uniquely strongly *-clean rings are also constructed.

Key words:uniquely *-exchange ring; strongly *-clean ring; uniquely strongly *-clean ring

中图分类号:O153

文献标志码:A

DOI:10.3969/j.issn.1000-2375.2016.03.002

文章编号:1000-2375(2016)03-0182-05

作者简介：王秀兰(1980-)，女，博士生，讲师，研究方向：clean 环，E-mail:lanxiu0614@163.com

基金项目：国家自然科学基金数学天元基金(11426200)资助

收稿日期:2015-09-09