考虑润滑油膜的深沟球轴承非线性动力学分析*

刘　伟，赵自强，王文中

(北京理工大学 机械与车辆学院，北京 100081)



考虑润滑油膜的深沟球轴承非线性动力学分析*

刘伟，赵自强，王文中

(北京理工大学 机械与车辆学院，北京 100081)

摘要：针对机床中使用的深沟球轴承，考虑了油膜阻尼和油膜切向摩擦力，建立了更符合实际工况的轴承运动微分方程。通过数值方法求解得到了轴承系统在不同转速、不同波纹度幅值下的分岔图、相图、轴心轨迹图和庞加莱图，以及考虑表面凹坑的动力学参数变化，并与未考虑润滑油膜影响的计算进行了比较。结果表明，润滑油膜的存在有利于减小轴承的振动，波纹度使系统的动力学行为更加复杂，而表面凹坑则降低了轴承的运转精度。

关键词：油膜阻尼；摩擦力；振动；表面波纹度；凹坑

在超精密机床中，滚动轴承的动力学行为决定主轴的回转精度，最终将影响零件加工质量。在其他机械装备中，滚动轴承同样是影响系统性能的关键环节，因此，建立完备的滚动轴承动力学模型，准确预测和分析轴承的动力学行为和性能非常重要。滚动轴承因制造工艺的制约，内外滚道表面存在波纹度；滚动轴承在运转过程中，轴承零件制造误差以及轴承零件的磨损或缺陷引起的激振力将导致轴承振动。

轴承的振动直接影响转子系统的运行状态，为了保证转子系统的平稳工作，许多学者开展了轴承振动的研究。N. Akturk等将钢球简化为无质量的非线性弹簧，将钢球与套圈之间的接触力用内圈三自由度方向的位移来表示，建立了球轴承的三自由度非线性振动模型[1]。M. Tiwari等分析了不同阻尼时径向游隙对系统动力学行为的影响，得到了系统的相图和轴心轨迹图[2]。

A. Choudhury等研究了在径向载荷作用下，表面波纹度引起的轴承振动[3]。S. P. Harsha等分别研究了考虑游隙、表面波纹度和滚动体数量变化时的球轴承动力学建模问题，得到了各种因素对轴承动力学性能的影响情况，但其模型中未考虑润滑油膜的影响[4-5]。H. Arslan和V. N. Patel等分析了内外滚道局部缺陷对轴承振动的影响[6-7]。J. Sopanen等建立了考虑表面波纹度和局部缺陷的深沟球轴承动力学模型，并分析了表面波纹度和局部缺陷对轴承动力学性能的影响[8-9]。

近几年，国内学者在轴承动力学建模方面开展了进一步的研究。张彤等以球轴承为研究对象，求解滚动体与内外圈在弹流润滑状态下的刚度-阻尼，并分析了轴承不同转速和游隙对轴承转子系统动态特性的影响[10-11]。顾晓辉等分析了考虑滚动轴承内外圈波纹度、径向间隙和非线性赫兹力作用下的滚动轴承-转子系统非线性动力学响应[12]。关贞珍等建立了轴承外圈、内圈和滚动体局部损伤故障非线性动力学模型，并进行了动力学仿真与分析[13]。

在大多数文献的计算中，并没有考虑到润滑油膜的影响，系统的阻尼往往根据经验取为常数。本文以深沟球轴承为对象，考虑油膜阻尼和油膜切向摩擦力，结合Hertz接触理论和运动学方程，推导滚动轴承的非线性轴承力，得到滚动轴承的运动学微分方程，采用四阶Runge-Kutta法求解轴承系统内圈中心的位移和速度，与未考虑油膜影响的计算进行比较；并在考虑滚道的表面波纹度和凹坑的前提下，分析油膜对轴承动力学特性的影响。

1深沟球轴承动力学模型

深沟球轴承的基本结构如图1所示。

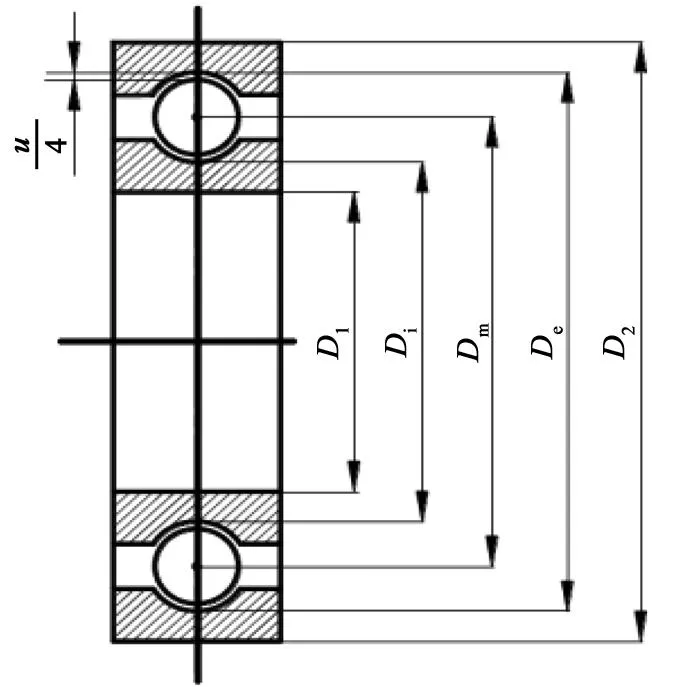
图1　深沟球轴承的基本结构

对于深沟球轴承，忽略径向游隙和高速下离心力对滚动体公转角速度的影响，滚动体的公转角速度为：

(1)

式中，ωi是轴承内圈角速度；Di是内滚道沟底圆直径；De是外滚道沟底圆直径。

轴承中钢球个数为Z，在内、外圈等距分布，外圈固定不动且为刚性套圈。由于径向力的作用，内圈中心在轴承径向平面的竖直方向位移为x，水平方向位移为y(见图2)。

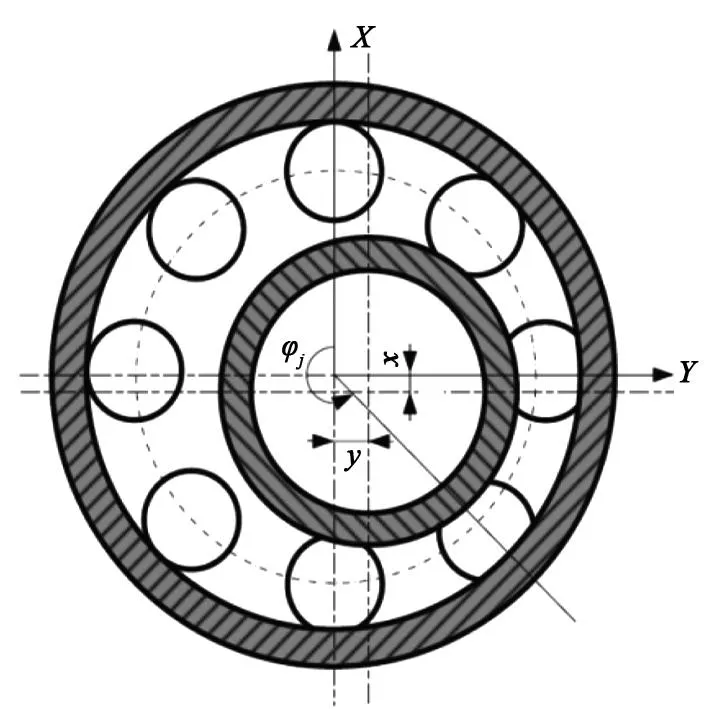
图2　内圈中心位移

在图2中的位置角φj处，内圈沟底位移可由下式表示：

dj=xcosφj+ysinφj

(2)

式中，φj是t时刻第j个钢球所在的位置角，表达为：

(3)

设深沟球轴承径向游隙为u，则在位置角φj处，钢球与滚道之间的接触弹性变形为：

δj=dj-u

(4)

由Hertz接触理论，钢球与滚道之间的接触载荷为：

(5)

式中，K是载荷-位移系数。

所有钢球对内滚道的作用力沿x和y方向的合力为：

(6)

由拉格朗日方程，得到轴承系统的运动微分方程：

(7)

式中，M是转子总质量；e是系统不平衡质量的偏心距，这里取0；C是总的油膜阻尼；Fx、Fy分别是油膜切向摩擦力F在x、y方向上的分量；Fr是径向载荷。

油膜阻尼的计算公式如下[14]：

(8)

(9)

式中，ci是钢球与内滚道之间的油膜阻尼；ce是钢球与外滚道之间的油膜阻尼(见图3)；C是球轴承的油膜阻尼；η是绝对粘度；ah是赫兹接触半径；h0是最小油膜厚度。ah和h0可以根据弹流润滑理论计算得到。图3中，在得到钢球与内、外滚道之间的油膜阻尼后，根据式9可计算得到总的油膜阻尼C。

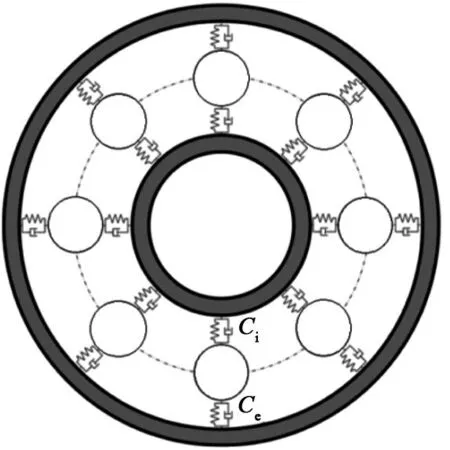
图3　球轴承油膜阻尼

可以用经验摩擦因数计算滚动体和滚道之间润滑油膜的切向摩擦力[15]。根据试验结果，把摩擦因数表示为最大接触应力和滑滚比的函数。为了简化计算，本文假设轴承处于良好润滑状态，摩擦因数取0.007，因而接触区内任一点的摩擦切应力可以表示为：

(10)

式中，μ是摩擦因数；Q是接触载荷；a是接触区域的长半轴；b是接触区域的短半轴。

式10中的切应力在接触区内积分可以得到总摩擦力F。

轴承-转子系统的运动微分方程组(式7)采用四阶Runge-Kutta法求解，计算中初值均取0，积分步长为激励周期的1/1 000，计算500个周期。为得到轴承-转子系统稳定后的响应，从第450个周期取值。计算所用轴承为SKF6002，轴承工况参数见表1。

表1　轴承工况参数

将轴承内圈转速作为系统的分岔参数，转速的变化范围取为8 000～12 000 r/min。考虑润滑油膜影响后，内圈中心在x和y方向的位移和速度随转速变化的分岔图分别如图4a～图4d所示。开始时，系统为一周期运动，随着转速的升高，进入混沌运动和倍周期运动交替进行的阶段，在转速为10 500～11 000 r/min时，出现了十周期运动和五周期运动，接着是拟周期运动，最后又变为一周期运动。对比可以看到，位移和速度的变化是同步的。

在未考虑润滑油膜影响的计算中，运动微分方程没有计算油膜阻尼，而是给定一个经验值，也没有考虑摩擦力的影响，未考虑润滑油膜(阻尼取为定值200 Ns/m)的结果分别如图4e～图4h所示。对比发现，考虑润滑油膜的影响后，x和y方向上的位移变化范围和速度波动范围有所缩小，并在转速为8 300～10 500 r/min时，使混沌运动区间出现了混沌运动和倍周期运动交替的情形。考虑到润滑油膜的减振、吸振作用，本文考虑油膜阻尼和摩擦力所得到的结果更符合轴承实际运转情况，结果也表明油膜对轴承振动有一定的抑制作用。

取转速为12 000 r/min时，研究周期运动状态下内圈中心的位移和速度，内圈中心在竖直和水平方向上的相图以及轴心轨迹图分别如图5a～图5c所示，相对应的庞加莱图分别如图5d～图5f所示。由图5可知，相图和轴心轨迹图均表现为一条封闭的曲线，而庞加莱图表现为一个点，表明系统在该转速下作一周期运动。

图4　轴心位移和速度随转速变化的分岔图

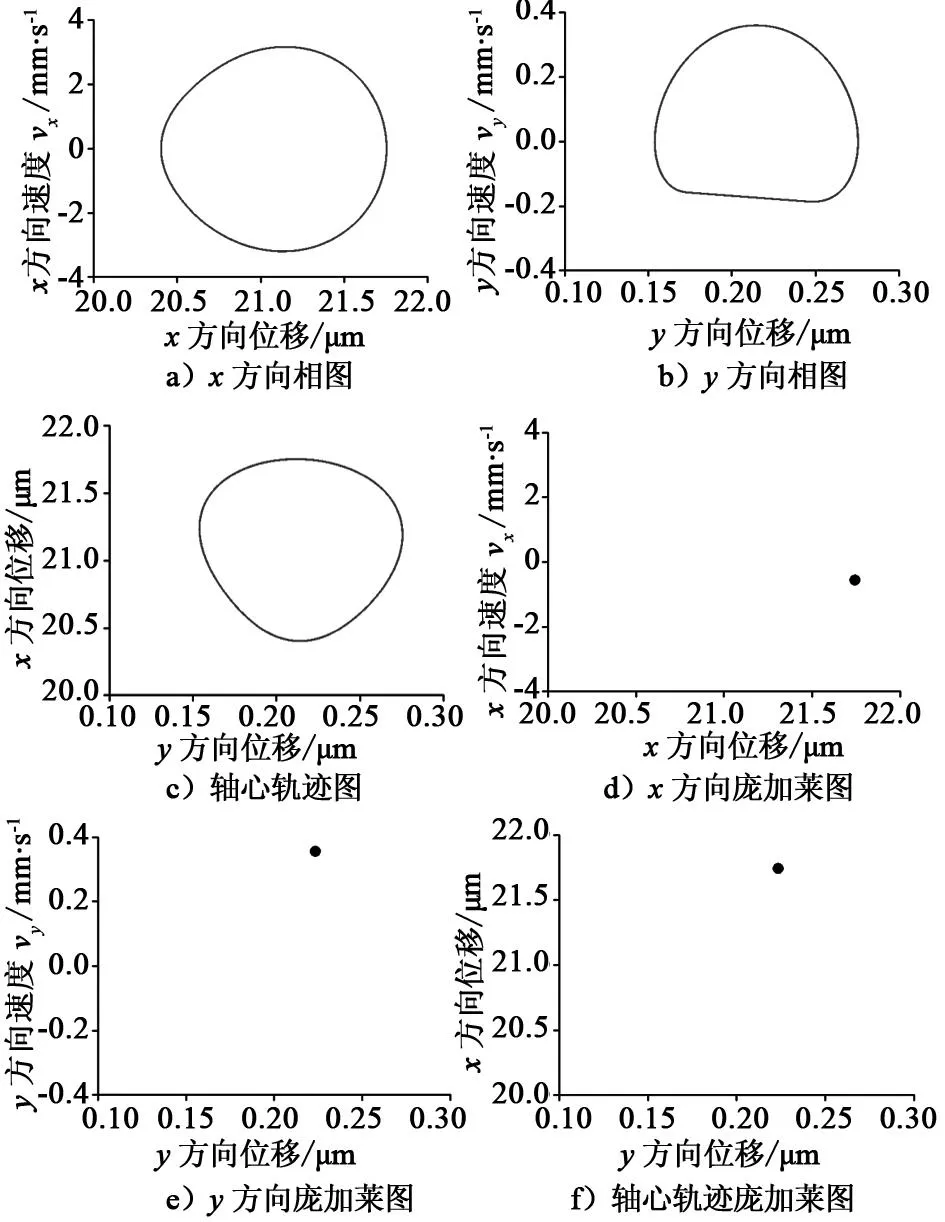
图5　一周期运动的位移和速度

2滚道表面波纹度的影响

在建立了考虑油膜阻尼和摩擦力的轴承动力学模型后，即可考虑滚道缺陷对轴承动力学行为的影响。假设内滚道存在波纹度，并为余弦函数形式，即：

(11)

式中，Ai是波纹度函数的幅值；θi是初始相位，这里取0；Pi是表面波纹度的阶数。

同理，外滚道表面波纹度函数为：

(12)

式中，Ae是外滚道波纹度函数的幅值；θe是初始相位，这里取0；Pe是外滚道表面波纹度的阶数。

设深沟球轴承的径向游隙为u，则考虑了滚道的表面波纹度以后，在位置角φj处，钢球与滚道之间的弹性变形量变为：

δj=dj-u+Pij-Pej

(13)

将式13代入式7即可建立考虑滚道表面波纹度的运动微分方程，仍采用四阶Runge-Kutta法求解。

以深沟球轴承SKF6002为例，轴承内圈转速为12 000 r/min，将外滚道的表面波纹度幅值作为轴承-转子系统分岔参数，幅值变化范围取2.0～12.0 μm，波纹度阶数为9，其余工况参数见表1。考虑润滑油膜影响后，内圈中心随外滚道的表面波纹度幅值变化的分岔图分别如图6a～图6d所示。由图6可知，随着幅值的增加，系统先作混沌运动，接着是二周期运动，然后是倍周期运动和混沌运动交替进行，最后是一周期运动。对比还可以看出，位移和速度是同步进入混沌运动的。未考虑油膜影响的计算结果分别如图6e～图6h所示。对比发现，考虑润滑油膜的影响之后，在幅值3.5～6.0 μm处出现了一段清晰的二周期运动区间，但在幅值11.4～11.8 μm处，再次进入了一小段混沌运动后才开始周期运动。

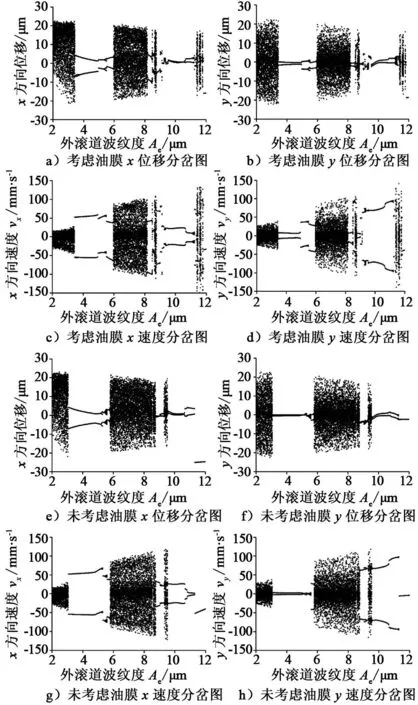
图6　轴心位移和速度随外滚道波纹度幅值变化的分岔图

图7　混沌运动的位移和速度

取波纹度幅值为7 μm时，研究混沌运动状态下内圈中心的位移和速度，内圈中心的相图和轴心轨迹图分别如图7a～图7c所示。由于系统作混沌运动，相图和轴心轨迹图均表现为复杂密集的曲线。对应的庞加莱图分别如图7d～图7f所示，表现为多个离散点。对比图5和图7，波纹度的存在使系统由周期运动变为混沌运动，导致了更大的振动幅值，使系统的动力学特性更加复杂。本模型也比较了不同波纹度阶数的结果，当外圈波纹度阶数与滚动轴承滚动体个数相同时，系统的动力学特性最为复杂，系统更易进入混沌运动状态，发生强烈振动。这与文献[16]的试验结果是一致的。

3滚道表面凹坑缺陷的影响

轴承在实际工作中可能在滚道表面产生凹坑等缺陷。内滚道表面的凹坑缺陷随内圈以角速度ωi旋转，则在t时刻，凹坑的位置角范围为：

(14)

式中，W是凹坑的宽度。

假设外圈固定，则外滚道凹坑缺陷的位置角范围为：

(15)

根据钢球的位置角和凹坑的位置角范围，即可判断在t时刻，钢球是否处于凹坑之中。引入变量ρi和ρe，如果钢球位于内滚道的凹坑中，则ρi=1，否则ρi=0；同理，如果钢球位于外滚道的凹坑中，则ρe=1，否则ρe=0。

假设深沟球轴承的径向游隙为u，则考虑了滚道表面的凹坑缺陷后，在位置角φj处，钢球与滚道之间的弹性变形量将变为：

δj=dj-u-ρihi-ρehe

(16)

式中，hi是内滚道凹坑引起的钢球中心变化的高度；he是外滚道凹坑引起的钢球中心变化的高度。

滚道上凹坑示意图如图8所示。在图8中，D是钢球直径，H是凹坑的高度，h是钢球中心变化的高度，由下式计算：

(17)

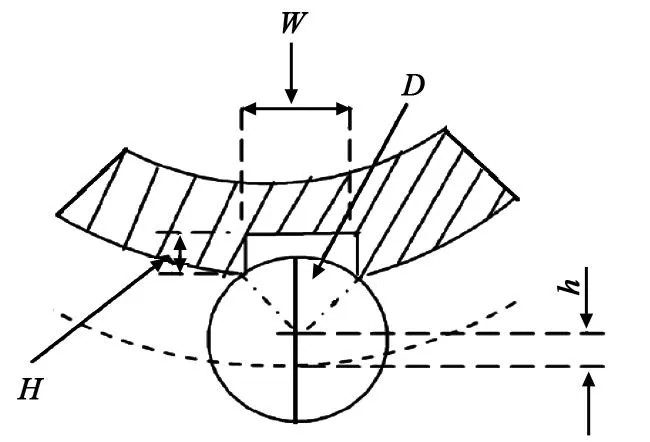
图8　滚道上凹坑示意图

将式16代入式7即可建立考虑滚道表面凹坑缺陷的运动微分方程，采用四阶Runge-Kutta法求解。

以深沟球轴承SKF6002为例，轴承内圈转速为12 000 r/min，其余工况参数见表1。考虑润滑油膜影响后，内滚道表面凹坑宽度为2.0 mm时轴承-转子系统的运动状态图分别如图9a～图9c所示，未考虑润滑油膜的结果分别如图9d～图9f所示。由于凹坑的存在，相图和轴心轨迹图为不规则的封闭曲线，对比图5的一周期运动，表面凹坑的存在降低了轴承的运转精度。

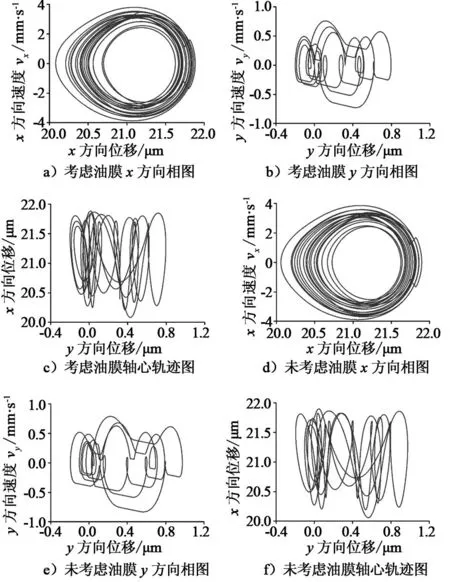
图9　考虑内滚道表面凹坑的位移和速度

与未考虑润滑油膜的结果进行比较，受油膜阻尼和摩擦力的影响，相图和轴心轨迹图的形状都向内收缩，进一步分析原因可知，通过计算得到的油膜阻尼比给定的经验值(200 Ns/m)要大，而阻尼增大会使表面凹坑对振动的影响减弱，这与本模型取得的结果是一致的。

4结语

综上所述，可以得出如下结论。

1)以深沟球轴承为对象，考虑了油膜阻尼和切向摩擦力对轴承系统动力学特性的影响，建立了更符合实际工况的滚动轴承动力学模型，求解得到了轴承-转子系统内圈中心的位移、速度等参数。

2)随转速的增加，系统由一周期运动状态进入混沌运动和倍周期运动交替状态，接着是拟周期运动，直至周期运动状态；考虑润滑油膜影响后，轴心的位移变化范围和速度波动范围有所缩小，润滑油膜的存在有利于减小轴承的振动。

3)随波纹度幅值的增加，系统先作混沌运动，接着是二周期运动，然后是倍周期运动和混沌运动交替进行，最后是一周期运动；波纹度的存在导致了更大的振动幅值，使系统的动力学特性更加复杂。

4)滚道表面的凹坑降低了轴承运转精度；油膜阻尼和摩擦力减弱了凹坑对轴承振动的影响。

参考文献

[1] Akturk N, Uneeb M, Gohar R. The effects of number of balls and preload on vibrations associated with ball bearings [J]. Journal of Tribology, 1997, 119:747-753.

[2] Tiwari M, Gupta K. Effect of radial internal clearance of a ball bearing on the dynamics of a balanced horizontal rotor [J]. Journal of Sound and Vibration, 2000, 238(5): 723-756.

[3] Choudhury A, Tandon N. A theoretical model to predict vibration response of rolling bearings to distributed defects under radial load [J]. Journal of Vibration and Acoustics, 1998, 120(1): 214-220.

[4] Harsha S P, Sandeep K, Prakash R. Non-linear dynamic behaviors of rolling element bearings due to surface waviness[J]. Journal of Sound and Vibration, 2004, 272: 557-580.

[5] Upadhyay S H, Jain S C, Harsha S P. Non-linear vibration signature analysis of a high-speed rotating shaft due to ball size variations and varying number of balls [J]. Journal of Multi-body Dynamics, 2009, 223: 83-105.

[6] Arslan H, Akturk N. An investigation of rolling element vibrations caused by local defects [J]. Journal of Tribology, 2008, 130(4): 1-12.

[7] Patel V N, Tandon N, Pandey R K. A dynamic model for vibration studies of deep groove ball bearings considering single and multiple defects in races [J]. Journal of Tribology, 2010, 132(4): 1-10.

[8] Sopanen J, Mikkola A. Dynamic model of a deep-groove ball bearing including localized and distributed defects, Part 1: theory [J]. Journal of Multi-body Dynamics, 2003, 217: 201-211.

[9] Sopanen J, Mikkola A. Dynamic model of a deep-groove ball bearing including localized and distributed defects, Part 2: implementation and results [J]. Journal of Multi-body Dynamics, 2003, 217: 213-223.

[10] 张彤, 王占彬, 王晓力. 弹流润滑球轴承-转子系统非线性动力学分析[J]. 北京理工大学学报, 2012, 32(3): 244-247.

[11] 刘大诚，史立伟. 球轴承涡轮增压器轴承-转子系统动力学分析与应用[J]. 新技术新工艺，2014(12): 53-55.

[12] 顾晓辉, 杨绍普, 刘永强, 等. 表面波纹度对滚动轴承-转子系统非线性振动的影响[J]. 振动与冲击, 2014, 33(8): 109-114.

[13] 关贞珍, 郑海起, 王彦刚, 等. 滚动轴承局部损伤故障动力学建模及仿真[J]. 振动、测试与诊断, 2012, 32(6): 950-955.

[14] Choudhury A, Tandon N. Vibration response of rolling element bearings in a rotor bearing system to a local defect under radial load [J]. Journal of Tribology, 2006, 128(2): 252-261.

[15] 邓四二, 贾群义, 王燕霜. 滚动轴承设计原理[M]. 北京: 中国标准出版社, 2008.

[16] Wardle F P. Vibration forces produced by waviness of the rolling surfaces of thrust loaded ball bearing, Part2: Experimental validation [J]. Proceeding of the Institute of Mechanical Engineering, 1988, 202(5): 305-312.

责任编辑郑练

Nonlinear Dynamics Analysis of Deep Groove Ball Bearings Considering the Impact of Lubricant Oil Film

LIU Wei, ZHAO Ziqiang, WANG Wenzhong

(School of Mechanical Engineering, Beijing Institute of Technology, Beijing 100081, China)

Abstract：For the deep groove ball bearings used for machine tools, the bearing differential equations of motion are established with consideration of the oil film damping and the tangential friction, which is much close to the actual working conditions. Bifurcation diagrams, phase diagrams, orbits of shaft center, and Poincare maps for the bearing-rotor system at different speeds, different waviness amplitude and dent are obtained by the numerical methods. The comparison is also conducted with the results without considering the effect of oil film. The results show that: the presence of the lubricant oil film tends to reduce the bearing vibration, the surface waviness makes dynamic behavior of the system be more complex, and the surface dent damages the bearing rotational accuracy.

Key words:oil film damping, friction, vibration, surface waviness, dent

中图分类号：TH 117.2

文献标志码:A

收稿日期：2015-10-27

作者简介：刘伟(1988-)，男，硕士研究生，主要从事机械设计及理论等方面的研究。

* 国家自然科学基金资助项目(51275045，51405017)

国家重点基础研究发展计划(973计划)项目(2011CB706602)