一道高中物理题的解析与变形

刘宏 马国敏 周素梅

【摘 要】本文由一道高中物理题出发，分析了这道题的求解方法；然后指出了学生对本题存在的疑问，并对疑问做了解答；然后在原题的基础上将题目变形，比较了匀速圆周运动与非匀速圆周运动的特点；最后总结了受力分析的一个小窍门。

【关键词】向心力；静摩擦力；趋势；切线；

笔者在讲解人教版高中物理必修2中的一道关于圆周运动的题时，发现学生对该题的向心力的来源并不清楚，并且在受力分析方面存在着错误的认识。

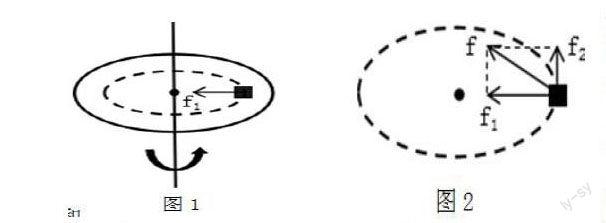
题目为人教版高中物理必修2中的一道课后习题，描述如下：一个圆盘在水平面内匀速转动，角速度是4rad/s。盘上距盘中心0.10m的位置有一个质量为0.10kg的小物体能够随圆盘一起运动，如图1所示。

（1）求小物体所受向心力的大小。

（2）关于小物体所受的向心力，甲、乙两人有不同意见：甲 认为这个向心力等于圆盘对小物体的静摩擦力，指向圆心；乙认为小物体有向前运动的趋势，静摩擦力方向和相对运动趋势方向相反，即向后，而不是与运动方向垂直，因此向心力不可能是静摩擦力。你的意见是什么？说明理由。

问题一让我们求小物体所受向心力的大小，小物体做匀速圆周运动，学生可以根据公式直接求得向心力的大小：F=mω2r=0.1×42×0.1N=0.16N。

问题二让我们判断向心力的来源，这是一个难点。我们先对物体进行受力分析，物体在竖直方向上受重力、圆盘对它的支持力，这时应指出物

体的轨迹是在圆盘上的一个圆周，圆心在转轴上且在轨迹的中心，这样便于学生找出向心力的来源，如图1所示，虚线是物体的轨迹。同时应提醒学生，物体能够随圆盘一起运动，即物体与圆盘之间没有相对运动，因此小物体不受滑动摩擦力。这时，学生经过思考可以判断出，是静摩擦力提供了向心力，其在轨迹平面内且方向指向圆心，如图1所示。即物体有沿半径方向远离圆心的趋势，则甲的说法是正确的，乙的说法是错误的。

在讲解的过程中笔者发现学生对本题的理解存在两个疑问，疑问一：如何判断出物体具有沿半径方向远离圆盘的趋势？疑问二：小物体由于惯性会有沿轨迹切线方向飞去的倾向，它是否在轨迹的切线方向上受静摩擦力？笔者对这两个疑问的解答如下：

在解答疑问一的时候，可以让学生根据自己的生活经验来感知，让学生回想生活中的一些场景，比如：汽车转弯的时候，坐在车里的人会有沿转弯半径方向向外倒的感觉，然后进一步说明圆盘做圆周运动就像汽车转弯一样，而小物体就像在汽车里的人，会有沿轨迹半径远离圆盘的趋势。让学生结合自身的经验去感知，有助于他们判断出小物体具有沿轨迹半径远离圆心的趋势。

在解答疑问二的时候，要告诉学生，小物体由于惯性会有沿轨迹切线方向飞去的倾向，这是由牛顿第一定律判断得出的，但是只有在惯性参照系中牛顿运动定律才成立，而转动的圆盘是非惯性参照系，即在圆盘参照系中牛顿第一定律是不成立的，因此，这个倾向是相对于地面参考系这个惯性参照系而言的，而不是相对于圆盘而言的。即小物体相对于圆盘没有沿切线飞去的倾向，故它在切线方向上不受静摩擦力。学生对牛顿运动定律成立的条件没有弄清楚，把相对于地面沿切线飞去的倾向当成了相对于圆盘沿切线飞去的倾向，导致了疑问的产生。我们也可以假设小物体在切线方向上受静摩擦力，则这个静摩擦力势必会改变小物体速度的大小，这就与小物体做匀速圆周运动的实际情况不符，从而判断出小物体在切线方向上不受静摩擦力。

在原题的基础上，可将题目变形，以达到巩固学生知识基础的目的。题目变形如下：小物体随圆盘一起做加速运动，这个时候小物体的向心力的来源是什么呢？这种情况下，静摩擦力不再指向圆心，其位于轨迹平面内且方向偏向小物体运动的方向，如图2所示。静摩擦力的一个分力f1指向圆心，提供向心力，另一个分力f2指向物体运动的方向，使其加速，则小物体做非匀变速圆周运动。将题目变形后，引导学生与原题进行对比，从而得出物体做匀速圆周运动与非匀速圆周运动的区别：物体做匀速圆周运动时，所受合外力充当向心力，方向指向圆心；物体做非匀速圆周运动时，所受合外力的一个分力充当向心力，此时合外力的方向并不指向圆心。

此题主要考察向心力的来源，受力分析是重点，在进行受力分析时，先把我们能确定的物体所受的力分析出来，如重力、支持力。如果学生难以判断某个力是否存在，则可以引导学生假设这个力存在，进而分析这样得到的结果是否与物体的实际运动状态一致，若不一致，则该力不存在。这种假设分析的方法比较容易被学生接受，是一种巧妙的受力分析的方法。

【参考文献】

[1]张大昌.普通高中课程标准实验教科书物理2必修[M].人民教育出版社，2010：28.

[2]刘广亚.例谈圆周运动解题技巧[J].数理化解题研究，2014，（7）.

[3]杨凌姿.高一物理中关于圆周运动的解题研究[J].数理化学习（高一二版），2015，（6）.

（西南大学物理科学与技术学院，重庆 400715）