蚁群算法下容量限制分配的路网结构可靠度分析

徐 旭，郑伟舜

(上海大学 土木工程系，上海 200072)

蚁群算法下容量限制分配的路网结构可靠度分析

徐 旭，郑伟舜

(上海大学 土木工程系，上海 200072)

为达到结合道路结构可靠度与道路网络可靠度的目的，分析了容量限制分配对道路网络结构可靠度产生的影响。容量可靠度采用交通统计的方法得出，并以容量可靠度0.4作为交通流量分配的标准。在蚁群优化算法的思想下，通过基于Ant-Cycle模型的容量限制分配方法，并对所测路网阻抗函数的参数重新进行了设定，从而对道路交通流量进行了分配。利用自编的基于软件MATLAB的蒙特卡罗程序求得容量限制分配前后的路面结构可靠度，进而求得对应的整个网络的结构可靠度。通过对上海市某一实际路网对比分析表明：路段拥堵时的容量限制分配尽管会提高相应路段的可靠度，但是被分配车流的道路可靠度会降低，进而最终的结果便是整个路网结构可靠度会降低。

交通运输工程；容量可靠度；容量限制；蚁群算法；路阻函数；道路网络可靠度

0 引 言

交通运输系统的一个重要本质特质就是随机性。交通运输系统随机性的特质要想合理反映，就必须得使用概率测度。而可靠性测度作为一种概率测度，对于反映运输系统的运行特征具有很好的效果。

目前，针对道路可靠度的研究主要包括两个方面。在路面结构可靠度方面，AASHTO[1]于1985年引入可靠度的设计方法，首次实现了对道路结构设计运用可靠度来计算；P．RAJBONGSHIi等[2]通过分析可靠度和费用因素，对沥青路面结构进行了优化设计；徐旭等[3]通过有限元法对沥青路面结构可靠度进行了计算分析。在路网可靠度方面，LIU Xuejie 等[4]探讨了选择关键路径的连通可靠性问题； Y．ASAKURA等[5]首次提出了行程时间可靠度的概念；喻泽文[6]对需求不确定情况下的道路网络容量可靠性进行研究，寻找出了道路网络中的薄弱部分，运用种种措施加以改善，使得突发事件出现时整个道路网络仍有条不紊。

到目前为止，对于路网可靠度和路面结构可靠度的研究已经有很多，但是将这两者结合起来研究的文献却鲜有。如果某段路的路面结构可靠度较低则从这条道路上走的车流会减少，而其他道路上的车流量会相应的增加，从而会影响整个路网的可靠度；相反若某个路网的道路网络可靠度很低的话，说明此网络的车流量太大，而车流量过大则势必会影响路段的结构可靠度。故仅仅单独分析某一方面是不完善的，需要将路网可靠度与路面结构可靠度结合起来分析。

徐旭等[7]将复杂的网络可靠度的研究方法引入到道路结构可靠度计算中，建立了基于道路网络的结构可靠度的研究方法。在此基础上，基于畅通可靠度与行程时间可靠度的道路网络结构可靠度得以研究。而针对可靠度常用的评价指标：行程时间可靠度估计对于假设条件的要求十分严苛，并容易因可靠度影响因素过多导致无法量化；畅通可靠度估计是以道路畅通为交通流量的分配标准的，但是相反地在真实道路中要解决的问题却是道路阻塞的问题；而连通可靠度没有直接考虑交通流量，只是考虑了两种最基本的运行状态，故上述3种评价指标均具有一定的局限性。所以，笔者以容量可靠度为评价指标，在容量限制条件下对道路网络结构可靠度进行分析。

1 容量可靠度

1.1 容量可靠度的定义和基本模型

A．CHEN等[8]通过研究连通可靠性所存在的不足之处，首先提出了容量可靠性这一概念；紧接着，A．CHEN等[9]通过深入分析，提出了求解容量可靠性的双层规划基本模型，从而完善了容量可靠度的理论基础。

目前，计算容量可靠度的方法[10-11]主要是在交通供需随机性、交通统计以及模糊估计下进行计算。但是鉴于交通供需随机性对于交通数据要求的长期性和详尽性、模糊估计的精确度和实用性差的客观事实，笔者采用交通统计的方法对容量可靠度进行计算。在后文实例中，对于所划定的道路网络，完全可以对交通量进行实地统计并对所需要的各个路段数据进行调查。

笔者提出以交通统计作为方法的容量可靠度计算如式(1):

RCCR=

(1)

式中：高峰小时内道路容量可满足交通需求的观测次数为在高峰小时内观测时,道路不发生拥挤、阻塞，车辆顺利通过时的次数。

1.2 容量可靠度与饱和度

饱和度在反映道路拥挤程度方面十分常用，可表示为道路流量V与实际通行能力C的比值。根据路网可靠度的计算结果，可以拟合某路网的容量可靠度和饱和度之间的关系。

2 路面可靠度

王祺国等[12]对道路路面结构可靠度进行了定义。其数学表达式为：

Rl=P(ld>ls)

(2)

Rσ=P(σR>σS)

(3)

式中：Rl，Rσ分别为考虑弯沉、弯拉应力的路面结构可靠度；ld，ls分别为设计弯沉、实际弯沉值；σR，σS分别为容许弯拉应力、实际弯拉应力值。

鉴于弯沉值控制指标的诸多优点以及蒙特卡洛法的相对精确性，笔者对于路面结构可靠度的研究以弯沉值作为控制指标，其计算方法则用蒙特卡洛法,并采用MATLAB数学软件与之相结合。

3 基于容量可靠度的路面可靠度

3.1 考虑容量可靠度的分析方法

笔者首先根据所划设的道路网络计算出其相应的容量可靠度和路面结构可靠度。在此基础上，对于单条道路超出其容量限制的部分以容量可靠度作为评判道路阻塞程度的标准，对交通流重新进行分配。在流量分配后需要根据所得的车流量重新计算此网络的路面结构可靠度。

3.2 容量限制分配方法

容量限制分配方法[13]是指当路段交通量增加到超过其容量承受力，即在路段通行能力的限制下，此路段上车辆的行驶速度会逐渐降低，并逐渐向与之相邻并且未达到饱和的路段上进行流量分配，从而完成重新选择“最短路径”过程的方法。

3.2.1 容量限制分配的蚁群优化算法

蚁群算法是由意大利学者M．DORIGO等[14-15]提出的。利用蚂蚁算法进行交通分配已经从理论和实践上证实不仅合理，而且可行[16]。笔者对于“最短路径”的搜索采用蚁群优化算法进行，而对于流量的加载则利用性能较好的Ant-Cycle模型。

3.2.2 算法实现

据孙华灿等[17]所述，在道路网络的容量限制分配方法中应用蚁群的优化算法在理论和技术上不仅合理而且可行。设计采用双层迭代机制：① 内迭代的目的是发现OD对间的最短路径，从而构建出完整的流量加载路径。② 外迭代的功能则是对路阻进行修正，并以此充当下一批蚁群的初始信息,从而体现网络的拥挤效应，最终使得分配结果趋于平衡。

3.2.3 路段阻抗函数

道路阻抗函数[18]是一个复杂的函数，其精确与否与分配是否能正确完成休戚相关。鉴于美国道路的一系列因素与国内巨大差异，为保证所建立的路段阻抗函数尽可能地符合客观存在的交通实际情况，必须得对目前常用的美国公路局BPR函数进行改进。

笔者的研究暂且针对某一特定的道路网络，因此可以通过真实地调查研究统计并综合考虑各种因素，重新标定美国公路局BPR函数中的参数。在实例中以上海市某一路网为例[19]，通过实际调查研究统计获取了大量实测数据，以快速路、主干路、次干路以及支路的分类形式对上海市此路网的阻抗函数重新进行参数标定。

4 道路网络可靠度

4.1 路段可靠度

路段可靠度为结合MATLAB程序的蒙特卡洛法计算出的单条道路的路面结构可靠度[20]

Rijk=P(ld>ls)

(4)

式中：Rijk为第i个OD对的第j条路径的第k条路段的路面结构可靠度。

4.2 路径可靠度

路径是由多个路段串联起来的一条存有起点和终点的路线，根据串并联原理可知路径可靠度为：

(5)

式中：Rij表示第i个OD对的第j条路径的可靠度。

4.3 OD对可靠度

OD对则是由上述不同的路径以并联的形式构成,故OD对可靠度为：

(6)

式中：Ri表示第i个OD对的可靠度。

需要注意的是：组成OD对的各条路径间很有可能存在共同的路段,即路径间不可避免地相交，因此必须用相容事件的概率公式对所求路集进行不交化处理，才能求得真实的OD对可靠度，计算如式(7)：

(7)

式中：P{S}为求道路网络正常的概率；Ai为输入与输出节点间的最小路集。

4.4 路网可靠度

由OD对可靠度确定的路网可靠度如式(8)：

(8)

式中：R为道路网络可靠度。

5 实例分析

以上海市某一区域的实际道路网络作为实例，截取其道路网络如图1(a)。为计算方便，可将图1(a)简化为道路网络简化图﹝图1(b)﹞。该道路网络中的道路可分为：主干道：道路1-22,3-25,4-9；次干道：其他所有。根据实地统计调查可知主干道通行能力为1 800 veh/h，次干道为1 500 veh/h，具体道路上的车流量如表1。主次干道的参数详见表2。设计年限累计车载量[21]见表3。

图1 道路网络Fig.1 Road network 表1 各条道路上的车流量 Table 1 Traffic volume on each road

道路编号车流量Q/(veh·h-1)1-2220122-2312327-2411563-2514894-9159310-1597516-211069

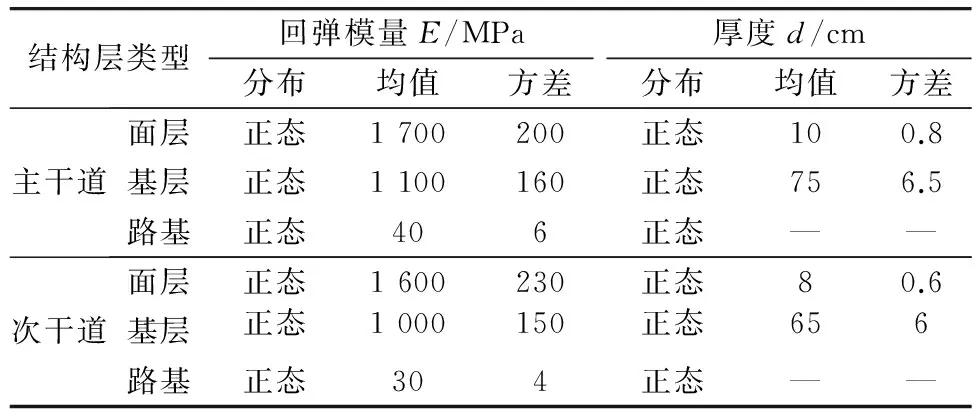
表2 主、次干道路面结构设计参数

表3 各条道路设计年限累及轴载次数

5.1 计算每条道路的结构可靠度

由式(2)通过MATLAB软件自己编制蒙特卡罗程序以计算路面结构可靠度，其计算结果如表4。

表4 各条道路结构可靠度

5.2 计算路网可靠度

将上述计算结果代入式(4)～(8)便可以计算出该路网的容量可靠度、路径可靠度、OD对可靠度和道路网络结构可靠度，其中道路网络结构可靠度为R=0.743 9。

5.3 计算各条道路的容量可靠度

根据前文饱和度的定义可计算出各条道路的饱和度，并根据基于交通统计的容量可靠度计算公式(1),可求得各条道路的容量可靠度(表5)。

表5 各条道路的容量可靠度

(续表5)

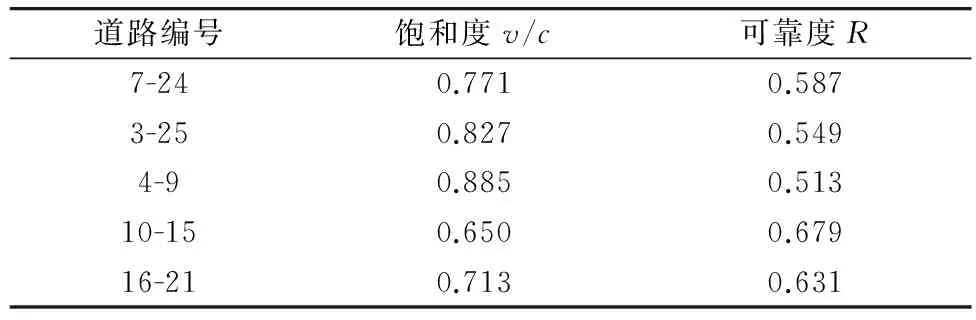
道路编号饱和度v/c可靠度R7-240.7710.5873-250.8270.5494-90.8850.51310-150.6500.67916-210.7130.631

根据表5，拟合出该道路网络饱和度与容量可靠度之间的关系(多为三次方关系)如下：

(9)

式中：V为路段交通量，veh/h；C为路段的通行能力，veh/h；RCRR为路段的容量可靠度；V/C为路段的饱和度。

5.4 蚁群优化算法下的交通容量限制分配

只有道路1～22的饱和度过大，且其车流量已经超出了通行能力。同时根据表6只有道路1～22的容量可靠度小于0.4，故笔者以容量可靠度0.4为标准，重新分配该道路上的超容量部分。

路阻函数采用美国联邦公路局(BPR)模型[22]：

(10)

式中：α1，β1为路况参数；va，Ca分别为路段a的交通量和对应的通行能力；ta(va)，ta(0)分别为路段a交通量为va，0时的行驶时间。

此外，蚁群模型参数设置为：蚂蚁数量为20；最大迭次为1 000；α=0.5；β=0.5；激素挥发为0.1；初始强度为10；最大强度为10；最小强度为4；释放强度为2。

据上文所述，对上海市的此段路网进行实际调查，可得各路段阻抗函数的相关参数[Ca，ta(0)，α1，β1]分别如表6。

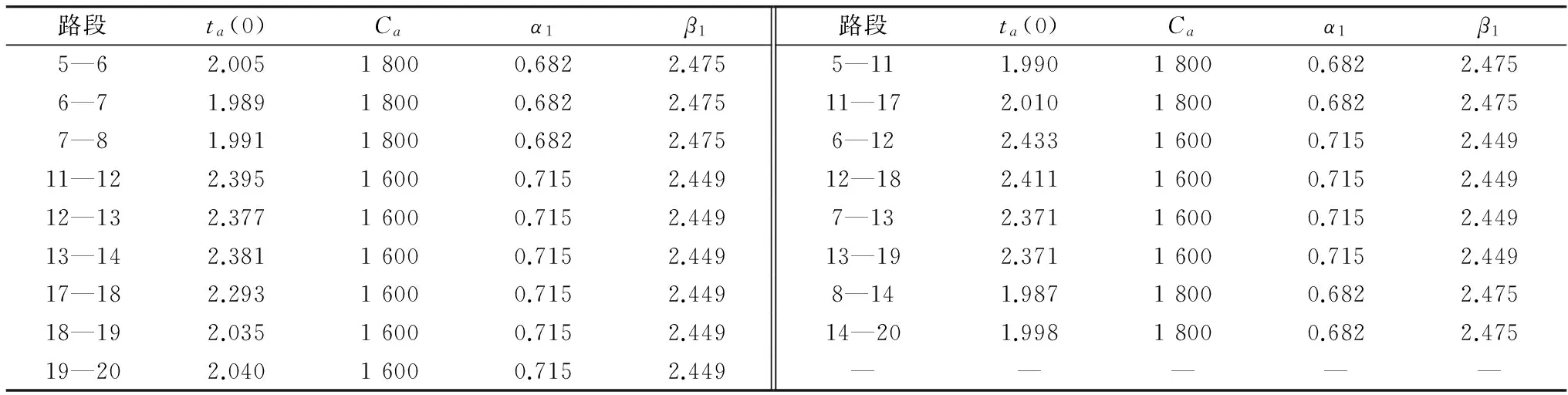
表6 路段阻抗函数参数设定

按照蚁群优化算法下的交通容量限制分配方法，通过程序运算，可以得到各路段的配流量和出行

时间的结果，见表7。

表7 路段交通量和出行时间

文中的道路网络比较复杂，如果对OD对的每个路径都计算不仅极大增加运算量，而且对最终结果影响不大；另一方面，若有太多的转弯次数反而会增加行车时间也不符合实际出行情况，所以笔者在选择OD对的路径时,转弯数要小于3。

以OD对(5，20)之间可行路径的行程时间为例，由表6可知：5-6-7-8-14-20,5-11-17-18-19-20,5-6-12-18-19-20,5-6-7-13-19-20,5-11-12-13-14-20的出行时间分别为15.198 6,15.195 1,15.197 5,15.198 0,15.196 3，均方差很小，因此Ant-Cycle模型下蚁群优化算法的容量限制分配方法是可行的。

5.5 计算流量分配后路网可靠度

容量限制分配后首先会导致各个路段的饱和度变化，将各个路段分配后的交通量代入前文所拟合的式(9)便可求出流量分配后的容量可靠度。

图2是交通流量分配后路段容量可靠度。由图2可见，容量可靠度均在0.4以上，可认为此道路不再拥堵；此外，容量限制分配后，各路段所对应的累计轴载作用次数也与之前不同，则需利用自己编制的蒙特卡罗程序重新求得容量限制分配后的路面结构可靠度如图3。并将其再次带入式(5)～(8)中，可得到容量限制分配后的路径可靠度、OD对可靠度和道路网络结构可靠度，其中道路网络结构可靠度为R=0.732 9。

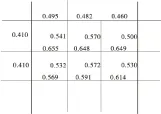
图2 交通流量分配后路段容量可靠度Fig.2 Capacity related reliability of each section after traffic volume allocation

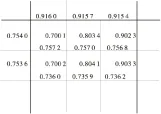
图3 交通流量分配后路段结构可靠度Fig.3 Structure reliability of each section after traffic volume allocation

5.6 计算结果对比分析

对比分析结果：对交通流进行容量限制分配后，同一路网的道路网络结构可靠度会降低。这表明在路网中，当某一条道路交通流量超过其容量限制值时，后续分配的交通量会重新选择新的“最短路径”，从而导致拥堵路段的路面结构可靠度和容量可靠度提高，但是其他被分配交通流的道路可靠度会降低，进而最终的结果便是整个路网可靠度会降低。

6 结 语

笔者通过MATLAB软件自己编制蒙特卡罗程序以求出各个路面的结构可靠度。将此路面结构可靠度依次带入路径可靠度、OD对可靠度、路网可靠度公式中，从而将路面结构可靠度与路网可靠度结合起来并求得路径可靠度、OD对可靠度以及最终的路网结构可靠度值。而交通分配是以容量可靠度0.4为标准，并通过容量限制条件下的改进蚁群算法为方法对交通流进行分配得到新的车流量分布。将此新的车流量重新带入自编程序中重新计算此道路网络的路径可靠度、OD对可靠度、路网结构可靠度，并与之前数据进行对比从而得到结论。

[1] AASHTO. Proposed AASHTO Guide for design of pavement structures[R].Washington, D. C.:AmericanAssociationofStateHighwayandTransportationOfficials,1985.

[2] RAJBONGSHI P, DAS A. Optimal asphalt pavement design considering cost and reliability[J].JournalofTransportationEngineering,2008,134(6):255- 261.

[3] 徐旭,王祺国.基于数值模拟的沥青路面结构可靠度分析[J].公路交通科技,2008,25(5):18- 22. XU Xu, WANG Qiguo. Analysis of the reliability of asphalt structure based on numerical simulation[J].JournalofHighwayandTransportaionResearchandDevelopment,2008,25(5):18- 22.

[4] LIU Xuejie, WEN Huimin, GAO Yong. The evaluation method of road network connectivity reliability based on key segments identification[C]// Sanya, Hainan :ProceedingCSO’09Proceedingsofthe2009InternationalJointConferenceonComputationalSciencesandOptimization, April 24- 25, 2009. Washington, D. C.: IEEE Computer Society, 2009:69- 71.

[5] ASAKURA Y, KASHIWADANI M. Road network reliability caused by daily fluctuation of traffic flow[C]// Sussex:Proceedingsofthe19thPTRCSummerAnnualMeeting. United Kingdom, Brighton: PTRC,1991:73- 84.

[6] 喻泽文.突发事件下路网关键路段的容量可靠性研究[J].公路工程,2014,39(1): 103- 107. YU Zewen. Study on capacity reliability of critical sections of road network under emergency[J].HighwayEngineering,2014,39(1):103- 107.

[7] 徐旭,付蓉.道路网络结构可靠度的研究[J].中外公路,2013,33(1):72- 76. XU Xu, FU Rong. The study of road network reliability[J].JournalofChina&ForeignHighway,2013,33(1):72- 76.

[8] CHEN A, YANG Hai, LO H K, et al. A capacity related reliability for transportation networks[J].JournalofAdvancedTransportation,1999,33(2):183- 200.

[9] CHEN A, YANG Hai, LO H K, et al. Capacity reliability of a road network: an assessment methodology and numerical results [J].TransportationResearchPartB:Methodological,2002,36(3):225- 252.

[10] 刘海旭,蒲云.诱导条件下的路网容量可靠性[J].科技通报,2005,21(4):476- 479. LIU Haixu, PU Yun. Road network capacity reliability in route guidance[J].BulletinofScienceandTechnology, 2005,21(4):476- 479.

[11] 张静芬,何杰,高梦起,等.交通影响分析中路网可靠性研究[J].交通科技,2008(2):95- 97. ZHANG Jingfen, HE Jie, GAO Mengqi, et al. Road reliability study in traffic impact analysis[J].TransportationScience&Technology,2008(2):95- 97.

[12] 王祺国,徐旭.响应面方法在路面可靠度分析中的应用[J].中外公路,2006,26(4):62- 64. WANG Qiguo, XU Xu. Response surface method in reliability analysis of pavement[J].JournalofChina&ForeignHighway,2006,26(4):62- 64.

[13] 田志立,周海涛.费用模型在容量限制交通分配中的应用[J].公路交通科技,1995,12(3):41- 47. TIAN Zhili, ZHOU Haitao. Application of cost model in capacity restrained traffic assignment[J].JournalofHighwayandTransportationResearchandDevelopment,1995,12(3):41- 47.

[14] DORIGO M, MANIEZZO V, COLORNI A. Ant system: optimization by a colony of cooperating agents[J]. IEEE Transactions on Systems, Man, and Cybernetics- Part B: Cybernetics,1996,26(1):29- 41.

[15] DORIGO M, GAMBARDELLA L M. Ant colony system: a cooperative learning approach to the traveling salesman problem[J].IEEETransactionsonEvolutionaryComputation,1997,1(1):53- 66.

[16] 侯立文,蒋馥.一种基于蚂蚁算法的交通分配方法及其应用[J].上海交通大学学报,2001,35(6):930- 933. HOU Liwen, JIANG Fu. Method of traffic allocation based on ant algorithm and its application[J].JournalofShanghaiJiaotongUniversity,2001,35(6):930- 933.

[17] 孙华灿,李旭宏,刘艳忠,等.容量限制分配的蚁群优化算法[J].东南大学学报(自然科学版),2009,39(1):177- 180. SUN Huacan, LI Xuhong, LIU Yanzhong, et al. Ant colony optimization arithmetic of capacity restraint traffic assignment[J].JournalofSoutheastUniversity(NaturalScienceEdition),2009,39(1):177- 180.

[18] 王文静,敬明,刘冬梅,等.基于LOGIT模型和BPR阻抗函数的容量限制- 多路径交通分配研究[J].公路交通科技,2012,29(增刊1):81- 85. WANG Wenjing, JING Ming, LIU Dongmei, et al. Study on capacity limitation- multipath routing traffic allocation based on LOGIT model and BPR impedance function [J].JournalofHighwayandTransportationResearchandDevelopment,2012,29(Supp1):81- 85.

[19] 何南,赵胜川.城市道路阻抗函数模型研究——以大连市为例[J].公路交通科技,2014,31(2):104- 108. HE Nan, ZHAO Shengchuan. Study on urban road impedance function model— a case study of Dalian city[J].JournalofHighwayandTransportationResearchandDevelopment,2014,31(2):104- 108.

[20] 徐旭,蔡锦波.交通流量分配对道路网络结构可靠度的影响[J].公路交通科技,2014,31(7):121- 128. XU Xu, CAI Jinbo. Influence of distribution of traffic volume on reliability of road network structure[J].JournalofHighwayandTransportationResearchandDevelopment,2014,31(7):121- 128.

[21] 黄兵,周正峰,贾宏财,等.半刚性基层沥青路面结构动力响应分析 [J].重庆交通大学学报(自然科学版),2014,33(1):47- 51. HUANG Bing, ZHOU Zhengfeng, JIA Hongcai, et al. Dynamic response of semi- rigid base asphalt pavement[J].JournalofChongqingJiaotongUniversity(NaturalScience),2014,33(1):47- 51.

[22] 徐勋倩,王亚萍.用蚂蚁算法处理固定需求交通平衡分配问题[J].南通工学院学报(自然科学版),2004,3(2):26- 27. XU Xunqian, WANG Yaping. Solving traffic equilibrium assignment problem of fixed traffic demand with ant algorithm[J].JournalofNantongInstituteofTechnology(NaturalScience),2004,3(2):26- 27.

Analysis on Reliability of Road Network Structure by Traffic Allocation due to Limited Capacity Using Ant Colony Algorithm

XU Xu, ZHENG Weishun

(Department of Civil Engineering, Shanghai University, Shanghai 200072, P.R.China)

The influence of traffic volume allocation due to limited capacity on the reliability of road network structure was analyzed in order to achieve the combination of the reliability of road network structure with the reliability of road network. The capacity reliability was achieved by traffic statistics and the capacity reliability of 0.4 was taken as criterion for traffic volume allocation. Based on the idea of ant-cycle algorithm and by method of traffic allocation due to capacity constraint and based on Ant-Cycle model, the parameter of impedance function of the road network under test was set anew for purpose of allocation of the road traffic volume. The reliabilities of pavement structure before and after allocation due to limited capacity were achieved by the self-prepared software of Monte Carlo MATLAB program to as to achieve the reliabity of corresponding whole network. The comparative analysis based on a real road network in Shanghai shows that although the reliability of related congested road section can be improved by means of traffic volume allocation according to limited capacity, the reliability of the road which received the allocation may decrease , which finally give rise to the reduced reliability of whole road network structure.

traffic and transportation engineering; capacity related reliability; capacity restraint; ant colony algorithm; impedance function; road network reliability

10.3969/j.issn.1674-0696.2016.05.25

2015-09-28；

2015-12-09

上海市教委科研创新项目(13YZ001)

徐 旭(1968—)，男，江苏南通人，教授，博士，主要从事复杂道路网络系统方面的研究。E-mail:xxu@mail.shu.edu.cn。

郑伟舜(1988—)，男，山东潍坊人，硕士研究生，主要从事复杂道路网络系统方面的研究。E-mail:15169012505@163.com。

U491.1+12

A

1674-0696(2016)05-127-06