梁板(柱)刚度比对地铁车站结构内力的影响研究
2016-05-25黎钜宏吴明辉李俊尧
黎钜宏,吴明辉,李俊尧,陶 熹
(1.广东省重工建筑设计院有限公司,广东 广州 510034;2. 武汉科技大学,湖北 武汉 430081;3. 佛山科学技术学院,广东 佛山 528000)
梁板(柱)刚度比对地铁车站结构内力的影响研究
黎钜宏1,吴明辉2,李俊尧3,陶 熹2
(1.广东省重工建筑设计院有限公司,广东 广州 510034;2. 武汉科技大学,湖北 武汉 430081;3. 佛山科学技术学院,广东 佛山 528000)
针对目前地铁车站结构设计中,结构截面刚度变化对车站结构内力的影响规律还有待进一步讨论分析的现状,以某地铁车站为例,利用ANSYS 13.0建立车站结构空间有限元模型。通过调整结构梁板刚度比和梁柱刚度比来探讨地铁车站结构内力的分布规律。由此得出结论:随着梁板刚度比的增大,各层板横向最大弯矩均减少,侧墙横向最大正弯矩增大,各层板纵梁最大弯矩均增大,柱子最大轴力减少;随着梁柱刚度比的增大,各层板纵梁最大弯矩和最大剪力以及柱子最大轴力均出现先增大后或减少或不变的现象,但以增大为主。
铁道工程;结构工程;空间分析;结构内力;梁板刚度比;梁柱刚度比;变化规律
现行的地铁地下车站结构设计大多采用支承在弹性地基上的平面简化模型进行结构内力分析。平面简化方法人为地将各层板、纵梁、柱子、侧墙等结构构件分离开来进行计算,忽略了它们之间的协同受力作用对结构内力的影响,从而不能很好地模拟结构实际受力状态,同时导致结构内力计算值偏大,经济上不合理。因此,对地铁车站这一复杂的空间结构进行三维分析计算,弄清车站结构内力在各种因素影响下的分布规律是非常有必要的[1]。
惠丽萍等[2]结合工程实例得出,对于设纵梁的地铁车站,采用传统的横断面计算法忽略了板与纵梁之间相对刚度对结构内力的影响,也忽略了纵梁两侧板的纵向弯矩,也忽略了支座处和跨中处板横向受力的差异。谢志秦等[3]利用SAP2000程序对现浇混凝土梁板体系进行了大量数值计算,分析了梁板相互作用的内在规律及影响规律,并提出了设计建议。蒋正跃等[4]以一个5层内框架厂房为例,得出了不同梁柱刚度比下类似结构合理简化的计算方法。基于目前采用空间分析手段对地铁车站在结构截面刚度变化下的内力变化规律研究得较少的现状,以某地铁车站为例,利用有限元分析软件ANSYS 13.0建立车站结构空间模型,探讨地铁车站主体结构内力随梁板刚度比和梁柱刚度比变化的分布规律。
1 车站概况
1.1 工程概况
某地铁站为地下两层12 m岛式站台车站,主体结构外包总长为201.50 m,标准段宽为21.10 m,有效站台中心结构顶板覆土厚度为2.0 m,底板底埋深为14.770 m。车站主体为双柱三跨钢筋混凝土箱型框架结构,采用明挖顺筑法施工。车站主体围护结构采用800 mm厚连续墙,插入深度约6 m。砼强度等级除柱子采用C50外,其余结构均采用C30。车站主体结构典型横剖面示意如图1。

图1 车站主体结构典型横剖面示意(单位:mm)Fig.1 A typical section diagram of the subway station main structure
1.2 工程地质条件
根据勘察地质报告,工程场地岩土层的物理力学参数如表1。

表1 岩土层物理力学参数
2 数值分析模型的建立
采用ANSYS软件建立车站空间有限元模型进行结构内力分析。在结构建模过程中,车站顶板、中板、底板、侧墙以及地下连续墙采用SHELL281单元模拟,不考虑地下连续墙的墙体接头;车站各层板纵梁及中柱采用BEAM189单元模拟;底板和地下连续墙低于底板以下的部分均利用SURF154单元来考虑岩土的弹性地基刚度。因地下连续墙墙底嵌固在全风化花岗岩层上,故对连续墙墙底施加垂直位移约束。车站底板直接支承在弹性地基上,底板与地基的摩擦力很大,且结构与荷载均对称,底板中轴在水平方向上位移很小,可略去不计。故对底板中轴位置处施加水平位移约束[5]。
数值分析模型长度取十跨车站标准段结构,共89 m。对结构边界处施加绕X轴,Y轴的转动约束和纵向位移约束。
3 梁板刚度比对结构内力的影响
梁板刚度比不仅对楼板支座负弯矩和跨中正弯矩有影响,而且还直接影响楼板中各板带承担的总弯矩在跨中与支座的分配关系[6]。传统横断面计算法对结构的真实性跟各层板与其相应纵梁的刚度比有很大的关系。通常来说,板厚与纵梁梁高之比介于0.2~0.5之间时,板对纵梁受力的影响是不容忽略的[2]。以下通过改变各层板的梁板刚度比,研究地铁车站主体结构内力随梁板刚度比变化的分布规律。车站标准段主体结构空间有限元模型如图2。

图2 结构空间有限元模型Fig. 2 The space finite element model of structure
定义梁板刚度比β:
(1)
式中:E为混凝土的弹性模量;Il为纵梁截面惯性矩,bl为纵梁梁宽,hl为纵梁梁高;Ib为车站每延米板的惯性矩;t为板厚。
根据式(1),保持纵梁梁宽bl不变,通过调整各层板厚度t,得出各层板纵梁的梁高hl。根据本工程实际情况,在周小华[7]研究的基础上,选取梁板刚度比β分别为5,10,15,20,25,30对地铁车站结构内力的影响。不同梁板刚度比β下各层板板厚与各层板纵梁梁高关系,如表2。计算结果如图3。
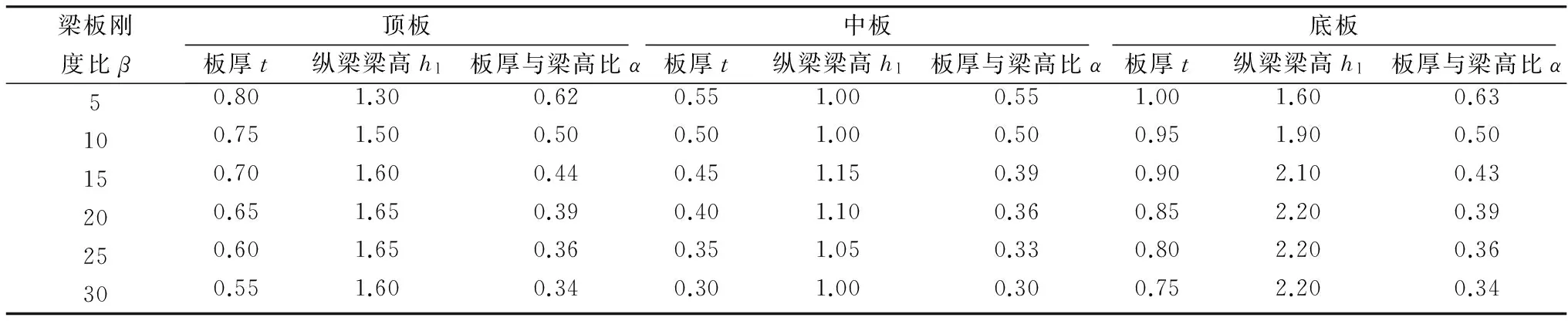
表2 不同梁板刚度比下板厚与纵梁梁高关系
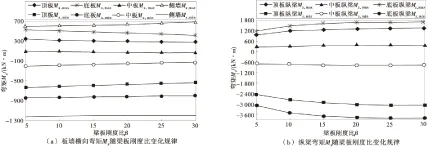

图3 车站主体结构内力随梁板刚度比变化规律Fig.3 Variation diagram of internal force of subway station main structure with different beam-slab stiffness ratio
由图3可知,车站各层板横向最大正弯矩Mx,max和横向最大负弯矩Mx,min均随着梁板刚度比β的增大而减少。其中,梁板刚度比由β=5增大到β=30时,顶、中、底板Mx,max分别减少了16.1%,29.3%,21.9%;顶、中、底板Mx,min分别减少了15.6%,42.4%,5.6%。随着梁板刚度比β的增大,侧墙横向最大正弯矩Mx,max增大,而横向最大负弯矩Mx,min基本不变,其值稳定在-1 200 kN·m附近。其中,梁板刚度比由β=5增大到β=30时,侧墙Mx,max增大了14.4%。每延米侧墙结构犹如一根两跨连续梁,顶、底板可看成连续梁两端支座,中板可看成连续梁中间支座。随着梁板刚度比β的增大,各层板刚度减少,但与顶板和底板相比,中板刚度更小,其对侧墙的支撑作用减弱得更快,从而使侧墙在车站站台层的横向最大正弯矩随着梁板刚度比的增大而增大。
车站顶板纵梁和底板纵梁最大正弯矩Mz,max和最大负弯矩Mz,min均随着梁板刚度比β的增大而增大。其中,梁板刚度比由β=5增大到β=30时,顶板纵梁和底板纵梁Mz,max分别增大了40.5%,42.5%;顶板纵梁和底板纵梁Mz,min分别增大了26.1%,23.6%。中板纵梁最大正弯矩Mz,max和最大负弯矩Mz,min随着梁板刚度比β的增大出现先增大后减少的现象,但以增大为主,转折点发生在β=15和β=20之间。其中,梁板刚度比由β=5增大到β=15时,中板纵梁Mz,max增大了25.8%,中板纵梁Mz,min增大了14.6%;梁板刚度比由β=15增大到β=30时,中板纵梁Mz,max减少了2.9%,中板纵梁Mz,min减少了1.9%。这主要是因为梁板刚度比由β=5增大到β=15时,中板纵梁梁高由h=1.0 m增大到h=1.15 m;β=15增大到β=30时,中板纵梁梁高由h=1.15 m减少为h=1.0 m。因此,纵梁弯矩虽以梁板刚度比影响为主,但纵梁梁高的影响也不容忽视。
车站顶板纵梁最大剪力Vy,max随着梁板刚度比β的增大出现了先增大后减少的现象。其中,梁板刚度比由β=5增大到β=20时,顶板纵梁Vy,max增大了6.0%;梁板刚度比由β=20增大到β=30时,顶板纵梁Vy,max减少了不到1.0%,其值基本稳定在2 800 kN。中板纵梁最大剪力Vy,max随梁板刚度比β的增大出现了先减少后增大,然后减少的现象。其中,梁板刚度比由β=5增大到β=10时,中板纵梁Vy,max减少了1.0%;梁板刚度比由β=10增大到β=15时,中板纵梁Vy,max增大了3.3%;梁板刚度比由β=15增大到β=30时,中板纵梁Vy,max减少了6.8%。底板纵梁最大剪力Vy,max随梁板刚度比β的增大出现了先增大后减少的现象。其中,梁板刚度比由β=5增大到β=20时,底板纵梁Vy,max增大了4.6%;梁板刚度比由β=20增大到β=30时,底板纵梁Vy,max减少了1.7%。与纵梁弯矩相比,各层板纵梁最大剪力Vy,max随梁板刚度比的增大,变化幅度均不大。
由表2可知,随着梁板刚度比的增大,顶板纵梁和底板纵梁梁高以增大为主,而中板纵梁梁高以减少为主。这跟各层板最大剪力的变化规律是一致的。因此,各层板纵梁最大剪力主要以梁高影响为主,而与梁板刚度比关系不大。
车站柱子最大轴力Ny,max随着梁板刚度比β的增大而减少。其中,梁板刚度比由β=5增大到β=30时,柱子Ny,max从-8 060 kN减少为-7 770 kN,减少幅度为290 kN。
综上所述,梁板刚度比的变化对各层板、侧墙和
各层板纵梁的弯矩以及柱子轴力影响比较明显,而对各层板纵梁剪力影响很小。由于纵梁的设置,地铁车站各层板弯矩分布规律发生了变化,各层板的受力状况得到了改善。梁板刚度比的增大使纵梁吸收弯矩迅速增加,而板弯距相应下降。因此,板参与了纵梁的工作,板梁是互相影响的。
4 梁柱刚度比对结构内力的影响
地铁车站作为一个复杂的空间结构属于超静定结构,其内力大小除取决于荷载的大小形式外,还取决于结构构件自身刚度以及与其相连的其他结构构件刚度,而结构构件刚度依赖于其截面尺寸[8]。以下通过改变各层板纵梁与柱的刚度比,研究地铁车站主体结构内力随梁柱刚度比变化的分布规律。
定义梁柱刚度比γ:
(2)
式中:Ic为柱截面惯性矩,Ic=bchc3/12,bc为柱截面宽,hc为柱截面高。
根据式(2),在γ,bc和hc不变的情况下,纵梁梁宽bl和纵梁梁高hl成反比。考虑到顶板纵梁和底板纵梁承受的荷载较大,需设计较大梁高值。而中板纵梁承受的荷载较少,同时为减少其梁高值,故在不同梁柱刚度比γ下,各层板纵梁梁宽均保持不变。且顶板纵梁梁宽由原来的1.2 m减少为1.1 m,中板纵梁梁宽由原来的0.9 m增大为1.0 m,底板纵梁梁宽由原来的1.2 m减少为1.0 m。
根据顶板纵梁bl=1.1 m,中板纵梁梁宽bl=1.0 m,底板纵梁梁宽bl=1.0 m,柱截面宽bc=0.7 m,通过调整柱截面高hc,得出各层板纵梁的梁高hl。当梁柱刚度比γ>3时,柱对梁的约束作用很小,此时可将柱作为梁的不动铰支座;当梁柱刚度比γ<3时,则需要考虑柱对梁的约束作用,此时梁柱节点为刚性节点。当梁柱刚度比γ=0.1~3.0时,两层两跨混凝土框架结构内力比较均衡;当梁柱刚度比γ>6.5时,框架柱的弯矩很小[9]。根据本工程实际情况,选取梁柱刚度比γ分别为2,4,6,8,10,12对地铁车站结构内力的影响。不同梁柱刚度比下各层板纵梁梁高与柱高关系,如表3。计算结果如图4。

表3 不同梁柱刚度比下纵梁梁高与柱高关系


图4 车站主体结构内力随梁柱刚度比变化规律Fig.4 Variation diagram of internal force of subway station main structure with different beam-column stiffness ratio
由图4可知,车站各层板和侧墙横向最大正弯矩Mx,max和横向最大负弯矩Mx,min随着梁柱刚度比γ的增大几乎没有变化。其中,顶板Mx,max和Mx,min分别稳定在310 kN·m,-627 kN·m附近;中板Mx,max和Mx,min分别稳定在75 kN·m,-150 kN·m附近;底板Mx,max和Mx,min分别稳定在487 kN·m,-856 kN·m附近;侧墙Mx,max和Mx,min分别稳定在636 kN·m,-1 240 kN·m附近。因此,梁柱刚度比变化对车站板墙结构几乎没有影响。
车站顶板纵梁、中板纵梁、底板纵梁最大正弯矩Mz,max和最大负弯矩Mz,min均随着梁柱刚度比γ的增大而出现先增大后或减少或不变的现象,但以增大为主,转折点发生在γ=10处。其中,梁柱刚度比由γ=2增大到γ=10时,顶板纵梁Mz,max和Mz,min分别增大了29.1%,21.1%,中板纵梁Mz,max和Mz,min分别增大了23.3%,8.5%,底板纵梁Mz,max和Mz,min分别增大了61.0%,33.8%;梁柱刚度比由γ=10增大到γ=12时,顶板纵梁Mz,max不变,其值为1 190 kN·m,顶板纵梁Mz,min由-2 810 kN·m减少为-2 800 kN·m,中板纵梁Mz,max不变,其值为498 kN·m,中板纵梁Mz,min由-903 kN·m减少为-899 kN·m,底板纵梁Mz,max由1 240 kN·m减少为1 230 kN·m,底板纵梁Mz,min由-3 090 kN·m减少为-3 070 kN·m。因此,梁柱刚度比在γ=2~10时对纵梁最大弯矩有影响,且对底板纵梁最大弯矩的影响更为明显。
车站顶板纵梁、中板纵梁和底板纵梁最大剪力Vy,max均随着梁柱刚度比γ的增大而出现先增大后减少现象,但以增大为主,转折点发生在γ=10处。其中,梁柱刚度比由γ=2增大到γ=10时,顶板纵梁、中板纵梁和底板纵梁的Vy,max分别增大了6.7%、9.2%和7.2%;梁柱刚度比由γ=10增大到γ=12时,顶板纵梁Vy,max由2 710 kN减少为2 700 kN,中板纵梁Vy,max由875 kN减少为872 kN,底板纵梁Vy,max由3 410 kN减少为3 390 kN。因此,梁柱刚度比对纵梁剪力影响不及对纵梁弯矩影响明显。
车站柱子最大轴力Ny,max随着梁柱刚度比γ的增大出现了先增大后减少的现象。其中,梁柱刚度比由γ=2增大到γ=8时,柱子Ny,max由-7 850 kN增大为-7 990 kN,增大幅度为140 kN;梁柱刚度比由γ=8增大到γ=12时,柱子Ny,max由-7 990 kN减少为-7 930 kN,减少幅度为60 kN。
5 结 论
1)梁板刚度比β主要对车站各层板横向最大弯矩、侧墙横向最大正弯矩、纵梁最大弯矩以及柱子最大轴力产生影响。随着梁板刚度比β的增大,各层板横向最大弯矩均减少;侧墙横向最大正弯矩增大;顶板纵梁和底板纵梁最大弯矩均增大;中板纵梁最大弯矩出现先增大后减少的现象,但以增大为主;柱子最大轴力减少。各层板纵梁弯矩虽以梁板刚度比影响为主,但纵梁梁高的影响也不容忽视。纵梁最大剪力主要以梁高影响为主,而与梁板刚度比关系不大。
2)梁柱刚度比γ主要对车站纵梁最大弯矩和最大剪力、柱子最大轴力产生影响,而对车站板墙弯矩基本上没影响。梁柱刚度比在γ=2~10时对纵梁最大弯矩和最大剪力有影响,且对纵梁最大剪力影响不及对纵梁最大弯矩影响明显。随着梁柱刚度比γ的增大,柱子最大轴力出现先增大后减少的现象。
3)在进行地铁车站结构内力分析时应充分考虑结构的空间效应,避免平面简化模型对各结构构件协同受力作用和中板开洞的忽略,合理地调配梁板刚度比和梁柱刚度比,使计算结果更加符合结构的真实受力状态。同时可减小保守设计时的工程资源浪费现象,实现地下结构工程的可持续发展。
[1] 王博. 明挖地铁车站整体建模结构受力分析[J]. 铁道标准设计,2012(11):75-88. WANG Bo. Structure stress analysis by integrated modeling for open-cut metro station[J].RailwayStandardDesign,2012(11):75-88.
[2] 惠丽萍,王良. 地铁车站结构设计中存在的问题[C]∥中国土木工程学会第十一届、隧道及地下工程分会第十三届年会论文集. 北京:中国土木工程学会,2004: 179-184. HUI Liping, WANG Liang. The existing problems in the civil design of metro station[C]∥AnnualMeetingConferenceProceedingsofthe11thInstitutionofCivilEngineeringandthe13thTunnelandUndergroundEngineeringBranch. Beijing: Civil Engineering Society of China,2004:179-184.
[3] 谢志秦,胡小勇. 现浇钢筋混凝土结构中梁与板协同作用研究[J]. 四川建筑科学研究,2011,37(5):70-73. XIE Zhiqin, HU Xiaoyong. Analysis of the interaction between beam and slab in cast-in-situ reinforced concrete building[J].SichuanBuildingScience,2011,37(5):70-73.
[4] 蒋正跃,龚爱民,张洪海,等. 梁柱刚度对结构计算模型和内力的影响[J]. 云南农业大学学报(自然科学版),2010,25(3):419-423. JIANG Zhengyue, GONG Aimin, ZHANG Honghai, et al. Effect of beam-column rigidity on structure calculating model and internal force[J].JournalofYunnanAgriculturalUniversity(NaturalScience),2010,25(3):419-423.
[5] 黎钜宏. 深圳地铁岗厦北站主体结构空间受力分析[J]. 土工基础,2014,28(3):13-17. LI Juhong. The analysis of the main structure of Gangxia north station of Shenzhen metro[J].SoilEngineeringandFoundation,2014,28(3):13-17.
[6] 夏冬桃,何英明,马杰,等. 梁板抗弯刚度比对板弯矩的影响分析[J]. 湖北工学院学报,2004,19(1):9-12. XIA Dongtao, HE Yingming, MA Jie, et al. Analysis of slab’s moment influenced by rigidity ratio of beam and slab[J].JournalofHubeiPolytechnicUniversity,2004,19(1):9-12.
[7] 周小华. 地铁车站箱型结构计算浅析[J]. 铁道建筑技术,2003(2): 14-16. ZHOU Xiaohua. Brief analysis of computation of box structure for metro station[J].RailwayConstructionTechnology,2003(2):14-16.
[8] 田雁新,孟焕陵,陈伯望.基于优化原理框架结构梁柱合理线刚度比研究[J]. 铁道科学与工程学报,2006,3(3):57-60. TIAN Yanxin, MENG Huanling, CHEN Bowang. Research on reasonable linear stiffness ratio of frames beam to column based on optimal principle[J].JournalofRailwayScienceandEngineering,2006,3(3):57-60.
[9] 张少钦,程华虎. 梁柱线刚度比对框架内力和侧移影响的分析[J]. 南昌航空大学学报(自然科学版),2011,25(3):84-88. ZHANG Shaoqin, CHENG Huahu. The analysis of the influence of beam-column line stiffness ratio on the internal force and lateral displacement of the frame[J].JournalofNanchangHangkongUniversity(NaturalSciences),2011,25(3):84-88.
Influence of Beam-slab(Column) Stiffness Ratio on Internal Force of Subway Station Structure
LI Juhong1,WU Minghui2,LI Junyao3,TAO Xi2
(1. Guangdong Zhonggong Architectural Design Institute CO., LTD., Guangzhou 510034, Guangdong,P.R.China; 2. Wuhan University of Science and Technology, Wuhan 430081, Hubei,P.R.China; 3. Foshan University, Foshan 528000, Guangdong, P.R.China)
For purpose of current situation that in current subway station structural design, the structural sectional rigidity variation influences internal force of the station structure and such influence principle calls for further investigation. By taking one real subway station for example, finite element model was built to simulate the station space by use of ANSYS 13.0. By adjusting the structural beam-slab rigidity ratio and slab-column rigidity ratio, the structural internal force distribution law of subway station was explored. Following conclusions are drawn as follows: With the increase of beam-slab rigidity ratio, the transverse maximum bending moment of slabs at all levels decreas is while the transverse maximum positive bending moment of side walls increasis and the maximum bending moment of slab longitudinal beams at all levels all increasis and column maximum axial force decreasis. With the increase of beam-column rigidity, the maximum bending moment of slab longitudinal beams at all levels and maximum shear force and column maximum axial force all showed signs of first increase then decrease or remaining unchanged, but increase is dominating.
railway engineering; structural engineering;spatial analysis; internal force of structure; the stiffness ratio of beam-slab; the stiffness of beam-column; law of variation
10.3969/j.issn.1674-0696.2016.05.16
2015-04-21;
2015-07-23
黎钜宏(1984—),男,广东佛山人,工程师,硕士,主要从事地下结构工程设计方面的研究。E-mail:112410612@qq.com。
U231+4
A
1674-0696(2016)05-074-05
