柯西中值定理的高阶推广

卢永翠，黄华平,2*，辛　华，刘婉贞，付　琴

(1湖北师范学院 数学与统计学院，湖北 黄石 435002;2湖北师范学院 文理学院，湖北 黄石 435002)



柯西中值定理的高阶推广

卢永翠1，黄华平1,2*，辛华1，刘婉贞1，付琴1

(1湖北师范学院 数学与统计学院，湖北 黄石 435002;2湖北师范学院 文理学院，湖北 黄石 435002)

摘要：利用数学归纳法，得到了高阶形式的柯西中值定理，推广了柯西中值公式.相比前人的结果而言，该结果更简洁，直观，实用.

关键词：柯西中值定理;柯西中值公式;连续;可导

柯西中值定理是拉格朗日中值定理的推广[1]，是微分学的基本定理之一[2].其几何意义为，用参数方程表示的曲线上至少有一点，它的切线平行于两端点所在的弦[1].柯西中值定理是数学分析中一个非常重要的定理[3]，它在判定函数的单调性，求不定式极限，证明等式和不等式等方面都有广泛的应用[4].然而，随着现代科技的发展，单一地使用柯西中值定理,已经远远不能满足人们的需要，因此探求它的推广公式，已经成为人们关注的热点之一.现今，已经呈现出了许多推广形式[2-8].基于此，本文得到了广义柯西中值定理，同时得到了柯西中值公式的高阶推广公式.相比前人的结果，本文的结果更方便,实用.

为方便读者，首先回顾一下如下定理.

设函数f(x)和g(x)满足下列条件：

1) 在闭区间[a,b]上都连续；

2)在开区间(a,b)内都可导；

3)对∀x∈(a,b),都有g'(x)≠0.

则∃ξ∈(a,b),使得:

此定理称为柯西中值定理，上述等式称为柯西中值公式[5-6].

1主要结果

定理1设函数f(x)和g(x)满足下列条件：

1) 在闭区间[a,b]上都连续；

2)在开区间(a,b)内都n阶可导；

3)对∀x∈(a,b),都有g(n)(x)≠0.

则∃ξ∈(a,b),使得:

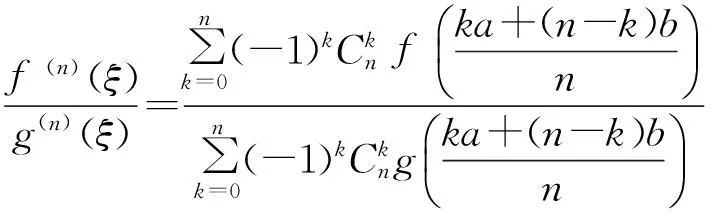
(1)

证明当n=1时，式(1) 就是柯西中值公式，结论显然.

假设当n=m时，式(1) 成立，即:

(2)

当n=m+1时，令:

则F(a)=0,G(a)=0,且:

(3)

显然F(x)和G(x)在区间[a,b]上满足柯西中值定理的条件，于是存在ξ1∈(a,b)，使得:

(4)

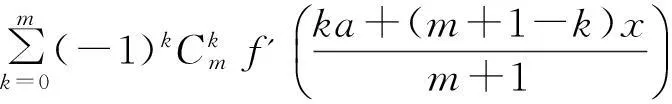
得到:

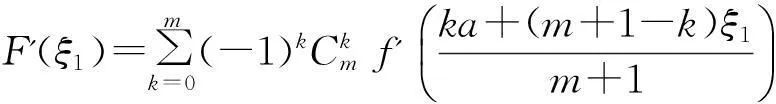
(5)

同理可得:

(6)

将式(5)和式(6)代入到式(4)可得:

(7)

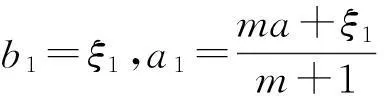
(8)

将式(8)代入到式(7)，并记f'(x)=f1(x),g'(x)=g1(x),可得:

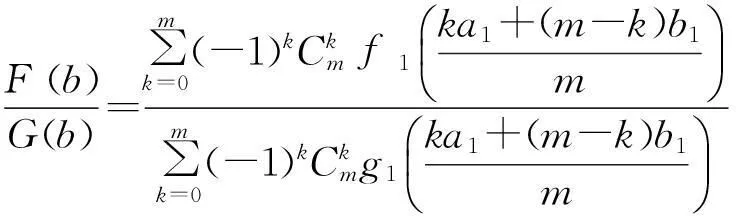
(9)

现对f1(x),g1(x)在区间[a1,b1]上应用m阶的柯西中值公式式(2)，于是存在:

(10)

最后，联立式(3), (9), (10)可得:

因此由数学归纳法可知式(1)对一切自然数都成立,证毕.

注相比文献[2]中的定理3，文献[6]中的命题2，文献[8]中的定理3，本文的定理1中的公式(1)更实用，因为它避免了前面定理中高阶行列式的复杂计算.

下面给出本定理的2个推论.

推论1设函数f(x)和g(x)满足下列条件：

1)在闭区间[a,b]上都连续；

2)在开区间(a,b)内都2阶可导；

3)对∀x∈(a,b),都有g''(x)≠0.

则∃ξ∈(a,b)，使得:

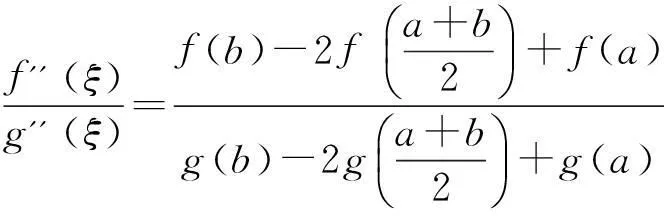
推论2设函数f(x)和g(x)满足下列条件：

1)在闭区间[a,b]上都连续；

2)在开区间(a,b)内都3阶可导；

3)对∀x∈(a,b),都有g'''(x)≠0.

则∃ξ∈(a,b)，使得:

参 考 文 献

[1]华东师范大学.数学分析(上册)[M].4版.北京：高等教育出版社，2010:128-136.

[2]张则增,周相泉,王娥.微分中值定理的推广[J].山东师范大学学报(自然科学版),1998,13(3)：323-325.

[3]王晓翊.柯西中值定理的两种推广[J].牡丹江师范学院学报(自然科学版),2013(1)：6-7.

[4]王娟，李力新，陈波，等.关于广义柯西中值定理的一种推广[J].内蒙古民族大学学报,2010，16(5)：1-2.

[5]吴校良,相伟.柯西中值定理的推广[J].内蒙古民族大学学报,2008，14(4)：1-2.

[6]郭森明,谢雪军.对柯西中值定理的若干认识[J].宜春学院学报(自然科学版),2006，28(6)：38,45.

[7]张发云.关于微分中值定理的一个推广[J].玉溪师专学报(自然科学版),1991(3)：69-72.

[8]尹枥.柯西中值定理的推广及其“中间点”的渐近性[J].滨州学院学报,2005,21(3)：74-77.

(责任编辑吴鸿霞)

Generalization of Cauchy Mean Value Theorem to High Order

LuYongcui1,HuangHuaping1,2*,XinHua1,LiuWanzhen1,FuQin1

(1School of Mathematics and Statistics,Hubei Normal University,Huangshi Hubei 435002;2School of Art and Science,Hubei Normal University,Huangshi Hubei 435002)

Abstract：In this paper,by using mathematical induction,Cauchy mean value theorem for high order case is given.Moreover,the corresponding Cauchy mean value formula is also extended.Compared with the previous methods in the literature,the obtained techniques are much simpler,more straightforward and applicable.

Key words：Cauchy mean value theorem;Cauchy mean value formula;Continuity;Differentiability

中图分类号：O172.1

文献标识码：A

文章编号：2095-4565(2016)02-0050-02

doi:10.3969/j.issn.2095-4565.2016.02.011

*通讯作者：黄华平，副教授，硕士，研究方向：函数论。

作者简介：卢永翠，本科生。

基金项目：湖北省教育厅科学研究计划指导性项目(项目编号：B2015137)；湖北师范学院本科生科研项目立项资助项目(项目编号：2014071)；湖北师范学院文理学院教学研究项目(项目编号：XJ201417)。

收稿日期：2016-01-26