一种基于滤波的分段点乘图像分割算法

李竹林，王 静

（延安大学 计算机学院，陕西 延安 716000）

一种基于滤波的分段点乘图像分割算法

李竹林，王 静

（延安大学 计算机学院，陕西 延安 716000）

图像分割的对图像识别、分析与理解具有重要的作用。文中针对含有噪声的图像，提出了一种分段点乘的图像分割算法。具体方法是首先根据灰度直方图确定图像的多灰度区域，然后实施分段点乘运算，使得图像中暗的部分更暗、亮的部分更亮，提高了目标和背景的对比度，突显了目标。最后用Canny算子进行边缘线分割，得到了较好的分割效果。该方法思路清晰，容易实现，具有较强的实用价值。

点乘运算；滤波；图像分割；Canny算子

图像分割是图像识别、跟踪、压缩、分析、理解以及立体匹配等处理的基础，是将图像表示为物理上有意义的连通区域的集合[1-2]。从第1个分割算法提出的1962年到2011年的半个世纪中，有关图像分割方法研究及的综述性的文献已达7.7万多篇[3-4]，但尚没有一种适合所有图像的通用算法，同时当给定一个实际应用后选择合适的分割算法仍是一个很麻烦的问题，且没有标准的方法[5-7]，所以图像分割算法一直是研究的热点和难点[8]。在实际的分割过程中，是将图像中有意义的特征部分提取出来，例如图像中的边缘、区域等。其中边缘特征是图像最基本的特征，经典的边缘检测方法有[9-10]：基于灰度直方图检测法、基于梯度检测法、Laplacian检测法及Canny检测法。基于边缘的图像分割适用于不同区域之间的边缘灰度值变化较大的情况，但难点是当图像的目标与背景对比度不大，灰度区域交叉又较多时，边缘检测的精度很难保证，不利于基于边缘检测的图像分割，而且边缘检测中的抗噪性与检测精度之间的矛盾也因此而变得更为尖锐[11-12]。文中针对上述问题，提出了一种基于分段点乘运算的灰度图像分割算法，使得图像中暗的部分更暗、亮的部分更亮，提高了目标和背景的对比度，进而改善图像的分割效果。

1 噪声去除

图像噪声是在图像拍摄和传输的过程中由于信号被干扰而引起的，是很难避免的。在一幅灰度图像中，将图像信号按照二维亮度f（x，y）分布，则噪声可认为是对亮度的干扰，用n（x，y）来表示。噪声是随机的，估计它的概率密度分布函数是有一定的难度或根本进行。因此，往往用均值、方差、等相关函数来描述噪声统计特征。一般，用噪声平方的均值E [n2（x，y）]来描述噪声的总功率，用噪声的方差E{（n（x，y）-E[n（x，y）]）2}描述噪声的交流功率，用噪声均值的平方{E[n（x，y）]}2描述噪声的直流功率[13]。

常见的噪声有：高斯噪声、椒盐噪声、均匀分布噪声、指数分布噪声等，其中高斯噪声与椒盐噪声在实际图像中比较常见[13]。

1.1 高斯噪声

高斯噪声又被称作是正态噪声，其概率密度函数为式（1），式中，z是图像灰度值，μ是z的期望值，σ是z的标准差。

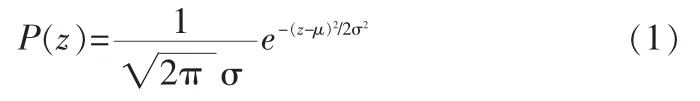
均值滤波是一种基于图像局部统计信息对图像进行滤波的方法，对于高斯噪声有较好的平滑效果[14]。为了取得更好的去噪效果，往往采取加权均值滤波方法[1]。

1.2 椒盐噪声

椒盐噪声也叫脉冲噪声。它是一种对图像质量的影响非常大的典型噪声。其概率密度函数为：

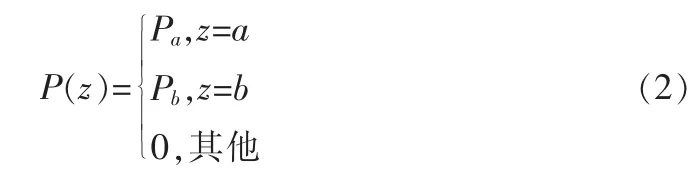
式中，当b＞a，则灰度值b所对应的像素点被表现为一个高亮度的盐点。相反，则值a所对应的像素点被表现为一个低暗度的胡椒点。若Pa或Pb为零，则椒盐噪声是单击脉冲。如果Pa和Pb都不为零，则是双击脉冲。

中值滤波法是一种典型的非线性去噪法，是基于排序统计理论的一种能有效去除噪声的处理技术[12]，其原理就是把数字图像中一点的灰度值用该点的一个邻域中各点值的中值代替，从而消除孤立的噪声点[15]。可表示为：

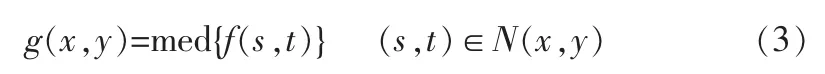
式中，f（s，t）、g（x，y）表示原图像和处理后的图像；N（x，y）是以（x，y）为中心的 n×n矩形滤波窗口（n为奇数）；med{}为图像的灰度值按照大小排序后，取中间的值。大量的应用证明，中值滤波既能除去盐点和胡椒点，而且能很好地保护图像的边缘轮廓信息[1，5，11]。

2 分段点乘

2.1 阈值确定

如果只用一个阈值分割称为单阈值方法，是最简单的一种。单阈值分割后的图像可定义为：

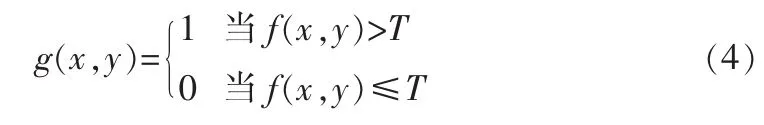
式中，x，y分别是图像的像素位置，f（x，y）表示原图像在（x，y）处的灰度值，T为图像阈值。

如果图像中有多个灰度值不同的区域，那么可以选择多阈值将每个像素分到合适的类别中去[3]。这种情况下，阈值T可表示为：

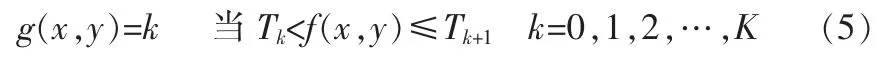
式中，Tk是一系列分割阈值，k是赋给分割后图像各个区域的不同标号。

既简单又直观的方法就是极小值点阈值。设h（z）代表直方图，那么极小值点对应的灰度值应满足[3]：

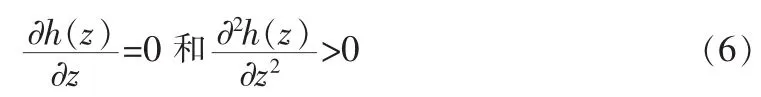
2.2 分段点乘

若能使得图像中亮的部分更亮，暗的部分更暗，即能突显图像中的目标，则便于图像分割。本文在式（3）阈值确定的基本思想，先选择合适的点乘值mk，使得灰度值大的更大，灰度值小的更小，则达到上述目的。这样，就得到基于阈值的点乘计算式（7）。

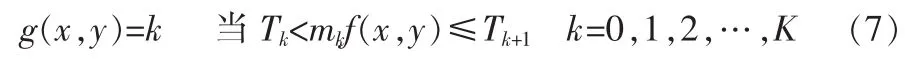
式中，mk为一组不同的点乘常量值，其他符号含义同式（5）。显然，究竟能否达到突显目标，mk的取值到关重要。在文中，应用256灰度图像，即0≤f（x，y）≤255，mk取值情况可以分以下3种情况：

1）mk取同一个大于 1的值。 若 f（x，y）＜1，则 f（x，y）×mk的积随着 f（x，y）的减小而快速减小；若 f（x，y）≥1，f（x，y）×mk的积随着f（x，y）的增大而快速增长。因此也能达到亮的部分更亮，暗的部分更暗。

2）mk取不同的两个值。若f（x，y）＜1，则 mk取小于1的值，使得f（x，y）×mk的积随着f（x，y）的减小而减小得更快；若f（x，y）≥1，则 mk取大于 1的值，f（x，y）×mk的积随着 f（x，y）的增大而快速增长。

3）根据图像灰度值的大小，mk取一组不同的值。这样实现了真正的分段点乘，使得效果更好，mk的大小，可以根据图像直方图的情况和经验值结合起来进行确定。

3 分段点乘的阈值图像分割算法

使用多阈值的分段点乘图像分割算法如下：

step1:噪声检测与去除。检测图像的质量，若含有噪声，则根据本第1节的噪声模型判断是高斯噪声还是椒盐噪声，并选择对应的去噪方法进行噪声滤除。

step2:阈值确定。求图像直方图包络线的极小值，记为Tk（k=0，1，2，…，K）。

step3:点乘运算。根据本文2.2节的方法大小确定点乘常量mk，实施分段点乘运算，形成新的图像。

step4:求g（x，y）的直方图包络线的极小值，确定新的（Tk，Tk+1）。

step5:若相邻的两个区域的灰度值相差不大，则可进行区域合并。

Step6:给所有的区域标以一组不同的标号k。

4 仿真实验与分析

4.1 模拟实验

取如图1（a）所示的256×256的Cameraman.jpg的灰度图，图1（b）是其统计直方图。根据直方图求得直方图包络线的峰谷的灰度极值分别为：60、145，峰顶的灰度极值分别为：12、130、165。 形成的灰度区域为：[0，8]，[8，17]、[17，101]、[101，143]，[143，190]，[190，255]。

对原图像实施分段点乘运算，根据划分的区域，取K=7，mk（k=0，1，…，K）分别取 0.2、0.5、0.8、1、1.1、1.15、1.2经过点乘运算后，形成新的灰度图像如图2（a），其直方图如图2（b）所示，也形成了新的灰度区域 [0，8]、[14，80]、[102，143]、[147，207]、[217、255]。若对图像实施如下的点乘运算，即取K=2，mk（k=0，1，…，K）分别取0.2和 1.20，这样当图像灰度值I（i，j）在[0，87]时，m0=0.2；当图像灰度值 I（i，j）在（87，256）时，m1=2。得到的点乘图像为图2（c），其直方图如图2（d）。此时，形成了直观明了的区域[0，14]和[172，255]。

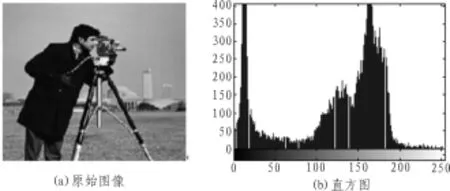
图1 原图像及其直方图

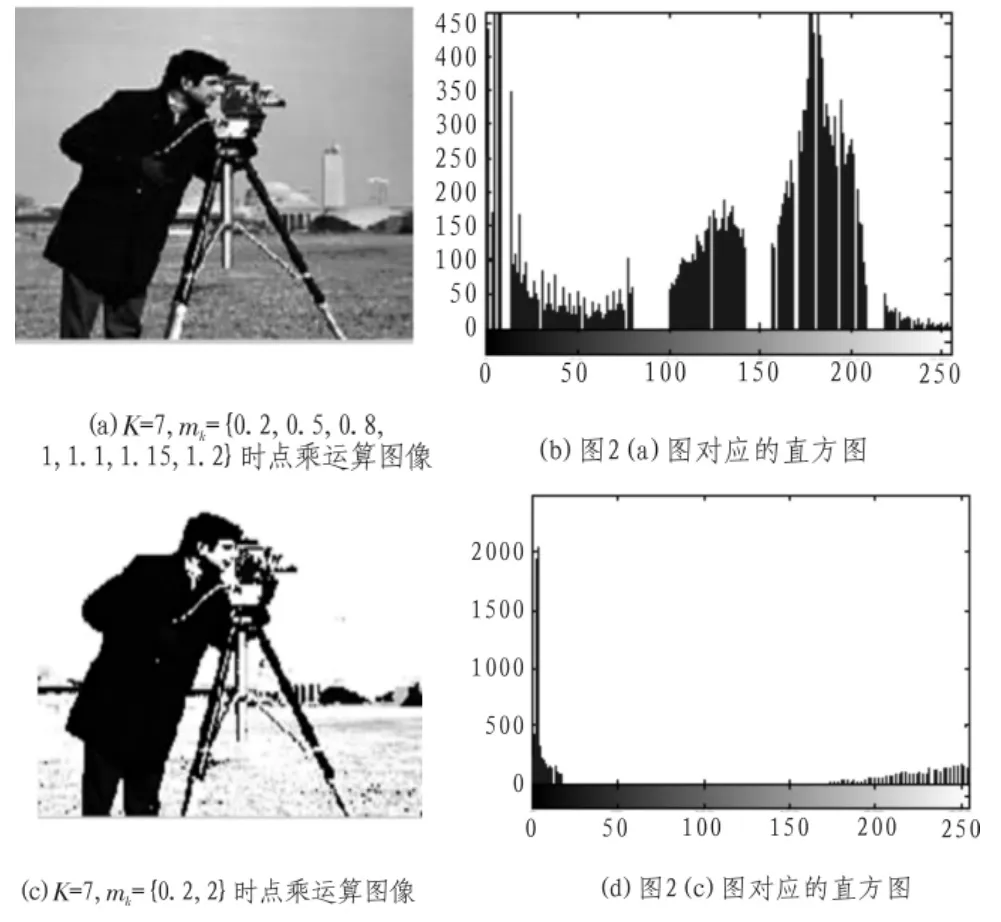
图2 点乘运算后的图像及其直方图

若不进行分段，直接用一个常数实现图像的点乘运算，则可得到如图3（a）所示的点乘运算图像，其Canny边缘分割图像如图 3（b）所示，图 3（c）是点乘运算后的图 2（c）的Canny边缘分割图像，与原图像的边缘分割图像（如图3（d））是相比较，突出了目标，取得了很好的效果。

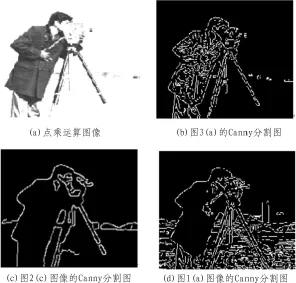
图3 Canny边缘分割效果对比

4.2 效果分析

对图3中的图像进行对比分析，可以看出：

1）与原图像相比较，实施点乘运算后，图像的目标与背景对比度增强了，相应地边缘分割图像也得到了明显的改善，可用图1与图2作对比，出可以图3中的（c）与（d）进行对照；

2）若用一个常数对原图像做点乘运算，则目标得到了增强，但背景也得到了增强，这样就不能达到增强对比度的效果，如图3（a）所示。相应地，得到的Canny分割图像边缘封闭性差；

3）若根据灰度值的大小进行分段点乘运算，则能达到增强对比度，突显目标的作用，如图2（a）、（c）所示。相应地，得到的Canny分割图像，目标突出且边缘封闭性好，如图3（c）所示。

5 结束语

图像分割是图像识别、跟踪、压缩、分析以及理解等处理的基础，由于分割算法的复杂度大与不易精准使得图像分割一直是图像研究领域的热点和难点。文中对图像实施了分段点乘运算，使得图像中暗的部分更暗、亮的部分更亮，突显了目标。在此基础上，使用了Canny边缘分割算法，取得了较好的分割效果。该方法思路清晰，容易实现，可以用在医学图像处理中。

[1]李弼程，彭天强.智能图像处理技术[M].北京：电子工业出版社，2004.

[2]何欣荣，张 刚.基于图像分割的改进立体匹配算法[J].微电子学与计算机，2014，31（12）:61-66.

[3]章毓晋.图像分割中基于过渡区技术的统计调查[J].计算机辅助设计与图形学学报，2015，27（3）:379-387.

[4]Zaitoun N M，Aqel M J.Survey on image segmentation techniques[J].Procedia Computer Science，2015，65（4）: 797-806.

[5]章毓晋.图像工程（中册）——图像分析[M].3版.北京：清华大学出版社，2012.

[6]林强，董平，林嘉宇.图割方法综述[J].微处理机，2015，36（1）:35-39.

[7]刘明君，姚丹.基于MATLAB的数字图像分割技术的研究[J].长春师范大学学报，2016，35（2）:46-48.

[8]朴春赫，赵海.基于水平集方法的交互式目标分割算法[J].计算机工程，2016，42（2）:229-235.

[9]王静.图像分割算法的分割算法的研究与应用[D].延安：延安大学，2015.

[10]李权，赵晋芳.几种图像去噪算法研究[J].商丘师范学院学报，2015，31（3）:27-32.

[11]李竹林，张根耀，等.图像立体匹配技术及其发展和应用[M].西安：陕西科学技术出版社，2007.

[12]赵晓莉.基于图像识别的冬小麦叶部主要病害诊断研究[D].郑州：河南农业大学，2014.

[13]贺东霞.数字图像去噪算法的研究与应用[D].延安：延安大学，2015.

[14]孙即祥.图像处理[M].北京:科学出版社，2004.

[15]钟涛，张建国，左俊彦.一种改进的中值滤波算法及其应用[J].云南大学学报：自然科学版，2015，37（4）:505-510.

An algorithm of piecewise point multiplication for image segmentation based on filtering

LI Zhu-lin，WANG Jing
（Institute of Computer Science，Yan’an University，Yan’an 716000，China）

Image segmentation is important to image recognition，analysis and understanding.For noisy image，the paper presents a subsection point multiplication method for gray image.Firstly，the multi gray regions of the image are determined according to the gray level histogram.Then the piecewise point multiplications are implemented，the piecewise point multiplication make the dark gray value becoming darker and the bright gray value becoming brighter，improve the contrast between the target and the background，and highlight the target.At last，the Canny operator is used to segment the edge line and a good result is obtained.The method is clear and easy to implement，and has a strong practical value.

point multiplication；filtering；image segmentation；canny operator

TN713

A

1674－6236（2016）23-0001-03

2016-04-02稿件编号：201604020

国家自然科学基金项目（61379026）；陕西省教育厅项目（2013JK1124）

李竹林（1972—），女，陕西佳县人，博士，副教授。研究方向：数字图像处理。