关注数学现实性 开发学习可能性——例析二、三年级学生学习“平方差”的可能性

浙江农林大学附属小学（311300）许向荣



关注数学现实性开发学习可能性
——例析二、三年级学生学习“平方差”的可能性

浙江农林大学附属小学（311300）许向荣

［摘要］可能性是学生的最伟大之处，把人引向更高的可能性是教育的本质所在。在传统教学观念里，二、三年级学生学习平方差公式简直是不可能的事。实际教学证明，只要学习材料组织恰当，探索过程引导得当，低年级学生学习这一内容完全是可能的。数学教学不仅要关注学生的现实性，更要走向开发学生学习的可能性。

［关键词］可能性现实性平方差

古希腊教育家普罗塔弋说：“教育的最终目的是要把作为人的独特本质的创新精神释放出来，使其成为能够自觉、自由创造的人。”要把第三学段（七年级）的平方差公式“a2-b2=（a+b）（a-b）”的教学内容下放到小学二、三年级中来学习，在传统教学观念上来看是“天方夜谭”。当下数学教学“四依四重”（即依照大纲重在要求，依赖课本重要例题，依靠传统重视讲解，依托习题重复训练）的现实性遮蔽了学习可能性的光辉。因此，在教学这部分内容时，我也曾犹豫彷徨，不敢接受任务。在特级教师张天孝老师的指导下，我学习了成尚荣的《从关注学生现实性走向开发可能性》的理论文献后，明确了“不可能的事往往是可能的”。因此怀着忐忑不安的心情设计并执教了平方差公式这个内容。实践告诉我：平方差公式在二、三年级学习是完全可能的，且效果令人满意。

【教学过程】

一、认识一个数的平方

师（课件出示）：说说下面各图分别由多少个小正方形组成。用什么方法可以比较快地知道小正方形的个数？

（教师利用学生介绍的方法逐图计算小正方形的个数：①3×3=9；②2×3=6；③4×3=12；④4×4=16；⑤6×6=36；⑥2×2=4；⑦5×5=25；⑧1×1=1。）

师：观察这些图形与算式，你有什么发现？

师（揭示）：3×3可以表示为32，读作3的平方，表示两个3相乘。你能用这个方法表示另外的算式吗？（请学生回答后再读一读，并说说32的意思）

（教师给出题目“想一想：72=□92=□102=□”）

【评析：通过对比，使学生认识到只有乘数相同，才能用平方数来表示，从而理解平方的含义。】

二、探究平方差计算规律

1.情境引入，初步感知

师（课件演示：从5×5的正方形左上角移走一个3×3的正方形）：请说一说，你看到了什么？谁能提个问题？

生1：还剩下多少个小正方形？

师：你会解答吗？请在本子上算一算。你是怎么算的？有不同的方法吗？

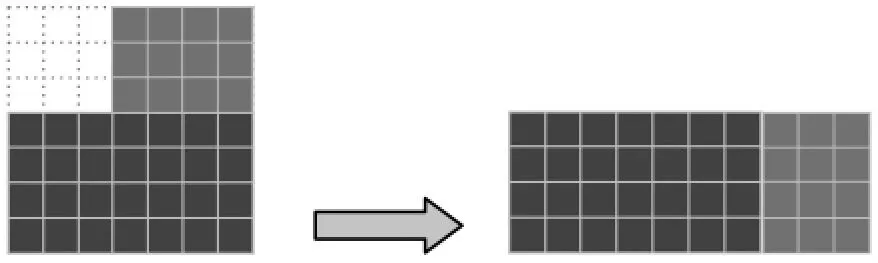
师（课件演示：将剩下图形分割成上下两个长方形。将上面部分旋转90度，再向右平移，向下平移，变成一个长方形）：你们有什么想法吗？

生2：变成长方形后，用8×2来计算小正方形的个数比较方便。

师：如果从5×5的大正方形中移走一个2×2的小正方形，剩下的图形还能变成长方形吗？（学生猜测后，教师用课件演示验证过程）

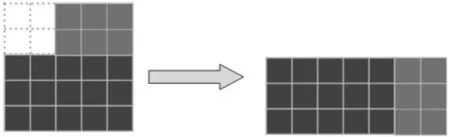
师：如果从6×6的正方形中移走一个4×4的小正方形呢？（学生猜测后，教师再次用课件演示验证过程）

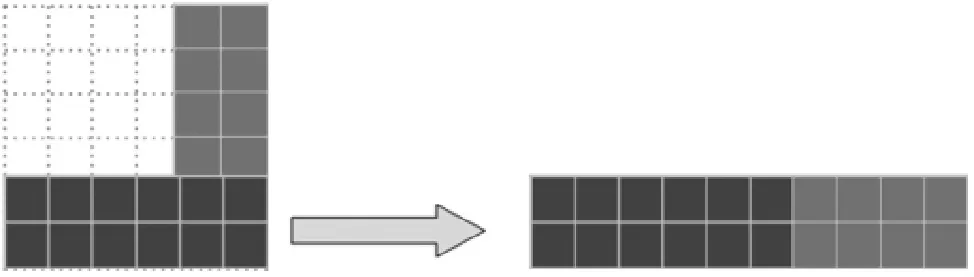
师：现在你有什么想法？

生3：从一个大正方形中移走一个小正方形后，剩下的图形能变成长方形。

【评析：利用直观演示，让学生感知从一个大正方形中移走一个小正方形后，剩下的图形通过分割、平移和旋转，都能得到一个长方形。由于是不完全归纳法，所以进行了三次不同图形的变换，使结论更为可靠。】

2.再次感知，探究规律

师：如果从7×7的大正方形中移走一个3×3的小正方形后，会怎样？

生1：会变成一个长方形。

师：现在的问题不是能不能变成长方形，而是会变成一个什么样的长方形？

（学生沉默）

生2：做一个看看。

师：如果不需要做就能知道它会变成什么样的，那才叫厉害呢!要不先回到前面几个例子中去找找规律，好吗？

（课件再次集中呈现前几个图形的变化）

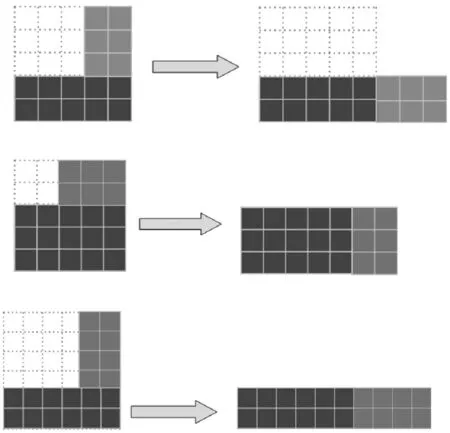
师：为什么第一次变出的是8×2的长方形，第二次变出的是7×3的长方形，而第三次变出的却是10×2的长方形呢？请结合图形看看“8”是怎么来的，“2”又是怎么得到的？

生3：第一个剩下图形的下面部分每层有5个，上面部分旋转后每层有3个，拼在一起是5+3=8（个）。大正方形原来有5层，移走3层后，剩下就是5-3=2（层）。

师：第二个图形中的7和3以及第三个图形中的10 和2又是怎么得到的？

（根据学生回答进行板书）

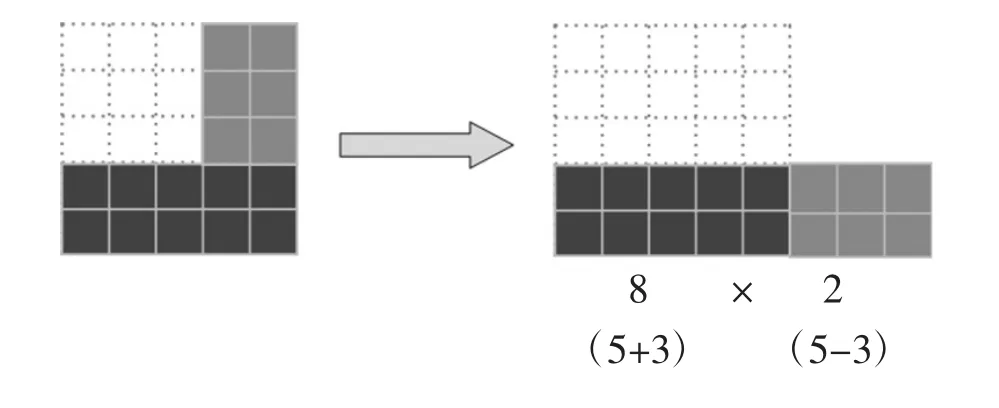
师：从7×7的正方形中移走一个3×3的正方形，会得到一个怎样的长方形呢？（学生想象、猜测并说明理由。课件演示验证过程）

师：如果从6×6的正方形中移走一个2×2的正方形呢？8×8中移走5×5呢？9×9中移走7×7呢？

【评析：这一环节主要让学生探寻图形变化的规律，即从一个大正方形中移走一个小正方形后，剩下的图形会变成一个什么样长方形。引导学生通过对图形变化前后的观察、比较，寻找长方形的长和宽与原来正方形边长的关系。】

3.沟通联系，揭示规律

师：观察上面这些图形，它们的形状发生了变化，但是什么没有变？

生：小正方形的个数没有变。

师：逐图计算变化前后小正方形的个数。第一幅图变化前小正方形的个数是5×5-3×3=25-9=16（个），变化后8×2=16（个），所以5×5-3×3=8×2。计算第2～4幅图，分别得到5×5-2×2=7×3、6×6-4×4=10×2、7×7-3×3=10×4。整理算式后得到：

（1）第一个式子左边5×5可以写作52，3×3可以写作32，右边8是由（5+3）得来，2是由（5-3）得到的，整理这个算式得到52-32=（5+3）×（5-3）；

（2）5×5-2×2=7×3、6×6-4×4=10×2、7×7-3×3=10×4。这几个算式你会整理吗？

（教师出示题目“想一想：82-52=□×□”）

三、练习

（1）42-22=□×□82-72=□×□102-92=□×□

（2）计算20152-20142

四、课堂小结

【感悟与反思】

本节课教学的全过程均借助了“数”与“形”的结合，把抽象的计算转化为形象的思考。在七年级的教材中，公式的推导主要是利用乘法分配律进行演绎推理。对低年级学生来说，这个过程无疑是艰辛而困难的。以形象直观思维为主的二、三年级学生学习这一内容时，必须借助图形的直观，通过观察、比较、想象、猜测、验证等活动，在充分感知的基础上，发现这一规律。在探究活动中，当学生发现所变出的长方形的长和宽与原来正方形边长的关系后，一切都变得简单且自然了。

钱学森把创造性思维理解为人类智力的核心，是形象与抽象思维的综合应用，其中形象思维是关键。这一观点我非常赞同。这样具有探索性的教材说明了一个问题，即只要学习材料组织恰当，探索过程得当，启发引导适当，二、三年级学生学习平方差公式是完全可能的。

从另一个角度看平方差公式，由两个正方形的差“a2-b2”可以得到一个指定的长方形，这个长方形的长是（a+b），宽是（a-b）。要让低年级的学生感悟这一规律是有一定难度的，因此，我分三个层次进行教学。第一步，通过直观展示，让学生发现从一个大正方形中移走一个小正方形，剩下的图形一定能变成一个长方形；第二步，通过让学生猜测从大正方形中移走一个小正方形，剩下的图形会变成一个怎样的长方形，激发学生的探究兴趣，继而引导学生观察、比较、想象和验证，直观发现长方形的长是两个正方形边长的和，长方形的宽是两个正方形边长的差。第三步，沟通联系，形成规律。

在练习部分，我设计了一道计算“20152-20142”的题目，把年份编进题目里，是为了增加练习的趣味性，更重要的是让学生体会平方差公式的作用，感悟数学知识的意义和价值，使学生认识到这个知识是非常有用的。

（责编金铃）

［中图分类号］G623.5

［文献标识码］A

［文章编号］1007-9068（2016）11-068