相机保护罐玻璃对摄影测量精度的影响规律分析与误差补偿

程志强，冯其强，易旺民，李宗春，王永强（. 解放军信息工程大学 地理空间信息学院，郑州 45000；. 北京卫星环境工程研究所，北京 00094）



相机保护罐玻璃对摄影测量精度的影响规律分析与误差补偿

程志强1，冯其强1，易旺民2，李宗春1，王永强1
（1. 解放军信息工程大学 地理空间信息学院，郑州 450001；2. 北京卫星环境工程研究所，北京 100094）

摘要：文章通过统计相机镜头处加玻璃前后点位的位移分布规律，选择合适数学模型，将玻璃对测量精度造成的影响减弱。现已完成相机保护罐玻璃对测量精度影响的实验，实验表明：加玻璃后像点坐标变化量最大约为5µm，该变化量的分布与镜头畸变规律相似。最后将其影响划归为径向畸变模型，并通过实验证明该方法能够有效减弱玻璃对测量精度影响。

关键词：真空高低温；数字工业摄影测量；相机保护罐；径向畸变；测量精度

http://www.bisee.ac.cnE-mail: htqhjgc@126.comTel:(010)68116407, 68116408, 68116544

0　引言

航天器变形量直接影响其收发信息的准确性与灵敏度[1]，故需对航天器进行热变形测量试验，以验证其设计、制造工艺以及装配等是否满足设计指标。试验过程中，被试设备受产品技术状态、试验环境参数、试验技术要求、设备尺寸和接口、视场遮挡等条件限制，并且由于人无法进入真空高低温环境中直接测量，必须采用适用于真空高低温环境下的非接触测量方式。数字工业摄影测量技术因具有非接触、劳动强度小、测量速度快、精度高、自动化程度高和对环境条件要求低等特点[2-3]，特别适宜于真空高低温环境下航天器的变形测量。

国内外采用数字摄影测量的方法对航天器的热变形进行测量已有很多成功的案例[4-7]。这些案例表明：真空高低温环境下的摄影测量，1）需要特殊材质的耐高低温回光反射标志作为标志点；2）需要微晶玻璃制作的基准尺提供绝对长度；3）须保证相机能在真空高低温环境下正常工作。目前常用方式是利用保护罐将相机与外界真空高低温环境隔离，但这种方式是否会对摄影测量精度产生影响却从未展开分析。本文通过对比相机镜头处加玻璃前后点位的位移分布规律，定量分析玻璃对测量精度的影响规律，最后类比相机的径向畸变规律并对误差作出补偿。

1　相机保护罩

相机的正常工作温度为0～35℃，而航天器变形测量的高低温环境的温度范围为-90～90℃；并且当环境气压降到500～600Pa左右时，可能发生电击穿，导致相机损坏。因此，必须要对相机进行保护。文献[7]中使用的相机保护罐（I-CAN）见图1。

图1　相机保护罐（I-CAN）Fig. 1　The protection tank of camera(I-CAN)

I-CAN为圆柱形，可正常工作的环境为：外部气压不低于3×10-8Pa，温度范围为-200～100℃。通过密封可以使罐内保持常压，通过温控可以使罐内温度保持在15～30℃。罐体的前端是光学玻璃窗口，相机镜头通过该窗口对目标进行拍摄。

2　玻璃对测量精度影响分析的理论基础

2.1加玻璃后的成像光路解析

从光学成像角度看，高反射标志将光原路返回，在CCD上形成像点。镜头前加玻璃后，由于光的折射使光路（见图2）发生偏移，造成像点有一定的位移（图2中的→表示偏移量），使得入射角1增大，入射点的位置在像片上的位置发生偏离，且距像主点的距离增大。

由光束分布图（图3）可知，全部光线构成一个以主光轴为中轴线的锥体。因此加玻璃前后的点位的变化量呈现一定的规律：矢量分布呈背离像主点的趋势。

以上是单纯从光学的角度分析玻璃对点位测量精度的影响。而在数字工业摄影测量中，像点的点位精度主要与相机性能、被测目标尺寸、像片数量和网形强度有关。已有研究表明：当相机装上保护罐后，拍摄的像片质量很好，完全可以满足摄影测量的要求[7]。因此，当被测物体尺寸、像片数量及网形条件固定的情况下，其影响待测点的坐标精度的因素就在于光的折射对镜头的影响，即相机镜头的畸变。

图2　反射标志的光路图Fig. 2　The light path of reflection

图3　光束分布图Fig. 3　The distribution of light

2.2相机畸变模型

十参数模型[8]是一种物理模型，依据相机成像过程中各种物理因素的影响而设计，是摄影测量领域，尤其是数字工业摄影测量领域应用最为广泛的相机畸变模型。十参数模型除包括主距f、像主点坐标(x0, y0)等相机内参数外，还包括镜头径向畸变、偏心畸变和像平面畸变等3类畸变参数[2, 9]。

径向畸变主要是由相机镜头中的透镜曲面形状不规则造成的，会使像点沿径向产生偏差。径向畸变有正、负2种，正的径向畸变使得内部的点向外扩散，尺寸随之变大，称为枕形畸变；负的径向畸变使得外部的点向内集中，尺寸随之缩小，称为桶形畸变。

径向畸变用多项式表示为

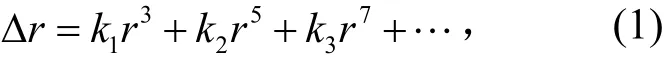
将其分解到x轴和y轴上，则有

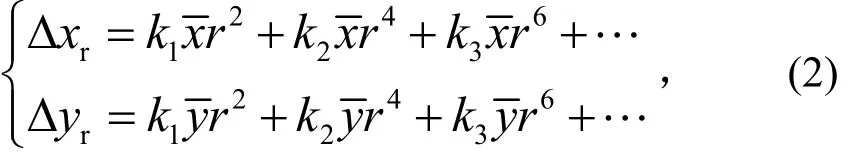
由于相机镜头系统中各透镜装配不到位等因素，使镜头器件的光学中心偏离了主轴线而引起像点偏离其理想位置所造成的畸变称为偏心畸变。偏心畸变既含有关于镜头主光轴对称的径向畸变，又含有关于镜头主光轴不对称的切向畸变。一般情况下，偏心畸变在数值上比径向畸变小得多，其表达式为

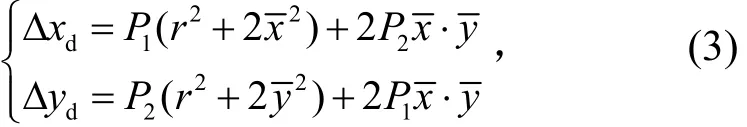
式中P1、P2为偏心畸变系数。

像平面畸变包括像平面内的平面畸变和由像平面不平引起的非平面畸变。传统相机的像平面畸变即为胶片平面不平引起的畸变，可以用多项式建模并改正。而数码相机的影像传感器由于采用离散的像敏单元成像，其非平面畸变很难用多项式来建模和准确描述。

像平面内的畸变通常可以简化成像素的长宽尺度比例因子和像平面x轴与y轴不正交所产生的畸变，其表达式为

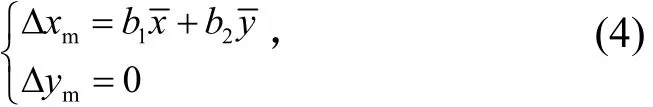
式中b1、b2为像平面内畸变系数。

综合径向畸变、偏心畸变和像平面畸变，十参数相机畸变模型可表示为

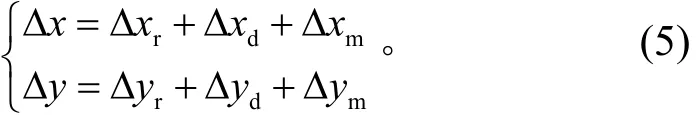
3　玻璃导致像点位移的实验及分析

为了更准确地验证加上玻璃后像点存在位移，进行2组实验：1）玻璃全部覆盖镜头；2）玻璃部分覆盖镜头。实验过程中要保证相机绝对静止，为此，先将相机安放在一个稳定的平台上，然后选择遥控的拍摄方式。实验场景见图4，场内均匀布设21个编码标志和512个标志点。

图4　标定场Fig. 4　Calibration field

3.1玻璃全部覆盖镜头

采集像片的流程定为：先拍摄一组镜头处无玻璃的（A组），再拍摄一组玻璃全部覆盖镜头的（B组），最后再拍摄一组镜头处无玻璃的（C组），如此循环100次。

将A组与C组像点坐标作差，若差值很小，即整个平台是稳定的。在此前提下，将B组与A组的像点坐标作差即为加玻璃前后每个像点的位移量。通过计算，标定场中像点位移如图5所示。

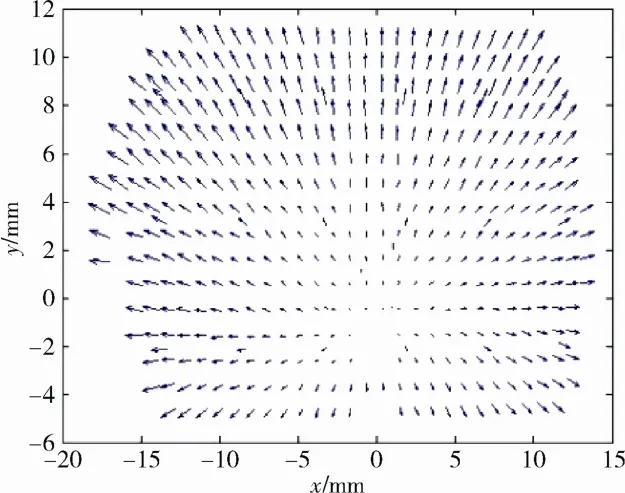
图5　加玻璃后像点位移分布Fig.5　The point displacement distribution after applying the glass

实验结果表明，加上玻璃以后，光的折射造成光路偏移，使得像点发生位移。所有像点位移分布呈现一定的规律：以像主点为圆心的圆，指向都背离像主点，且距像主点越远位移越大。为了进一步验证实验结论的准确性，进行第二组实验，当玻璃部分覆盖镜头时，比较同一条件下被玻璃覆盖的像点与未被覆盖的像点差值。

3.2玻璃部分覆盖镜头

同上个实验一样，将相机安放在稳定的平台上，首先将玻璃完全覆盖镜头，然后逐渐移动玻璃，遥控拍摄数张像片，直至镜头处没有玻璃。最终通过计算可得出像点位移情况如图6所示。

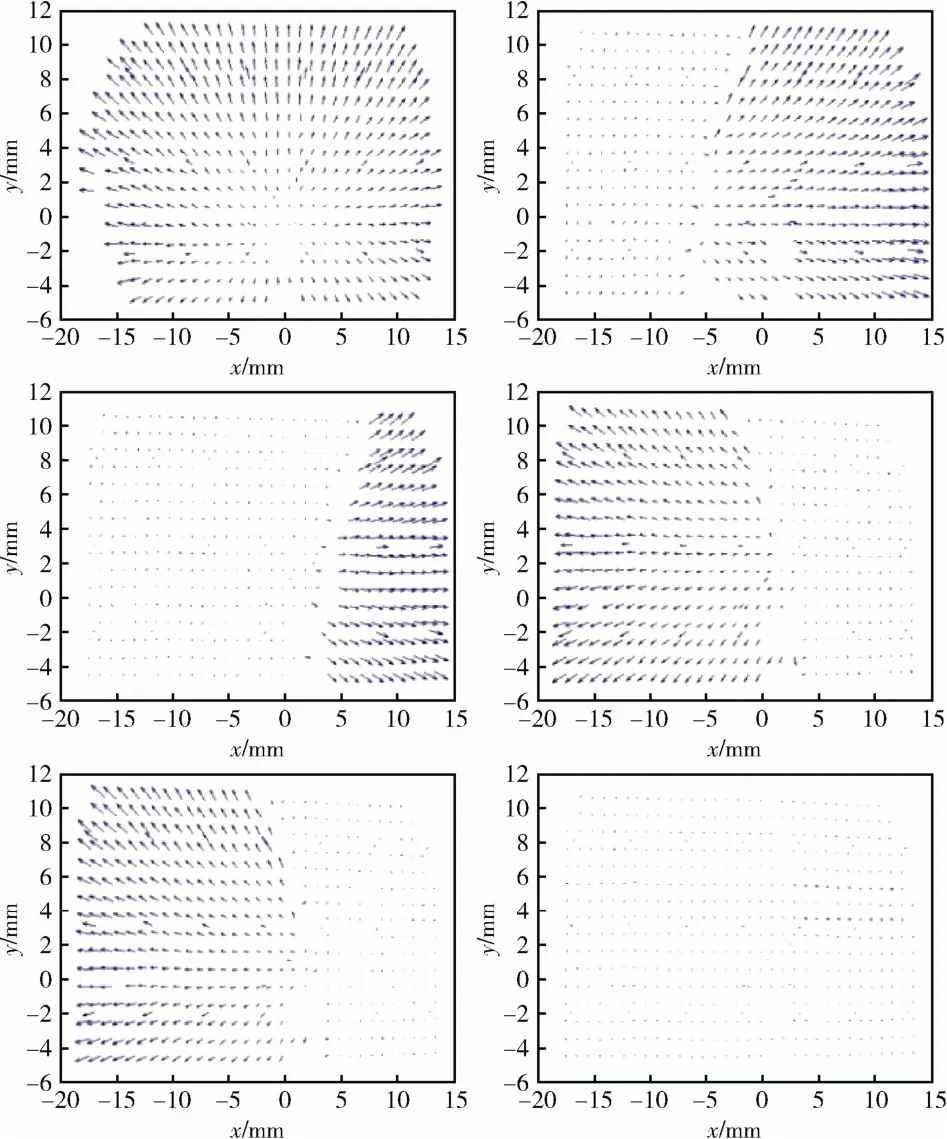
图6　玻璃移动过程中像点位移变化情况Fig. 6　The point displacement with the moving of glass

从图6可看出，移动玻璃的位置，其点位坐标发生变化的区域也会随之改变。因此可得出结论：当只考虑光的折射对点位测量精度影响时，加玻璃后像点坐标变化量最大约为5µm，并且其变化规律是以像主点为圆心的圆，指向都背离像主点，且距像主点越远位移越大。通过对比观察加上玻璃后的位移矢量图可知，径向畸变引起像点偏移的矢量特征及分布规律与实验结果十分相似。

为验证加设玻璃对像点位移的影响规律相似于相机径向畸变，分别采用厚度为4mm和5mm 的2块玻璃进行全覆盖镜头的摄影测量实验，并采用十参数模型在覆盖玻璃前后对相机进行严格校检，所得各类畸变参数如表1所示。

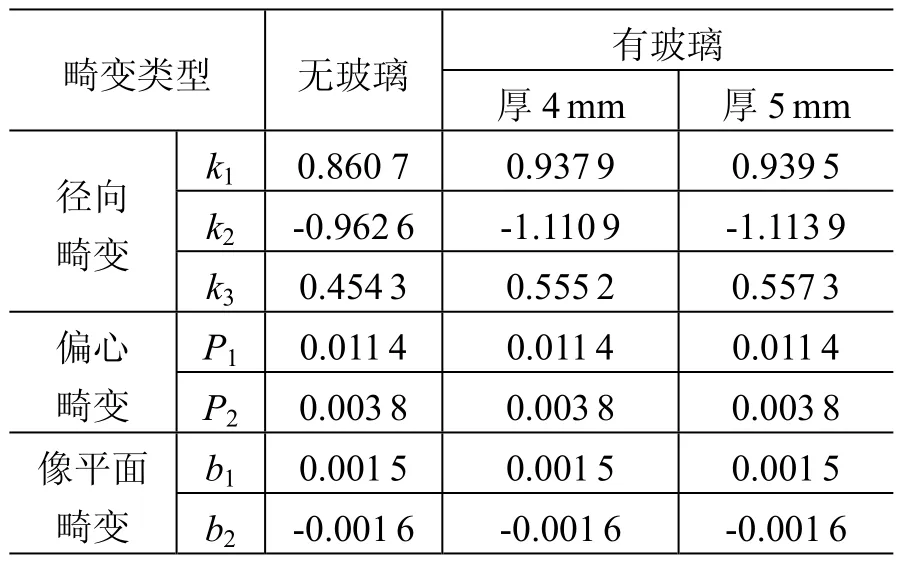
表1　各类畸变参数值Table 1　Various distortion parameters

通过对各类畸变参数的数值对比可知：加玻璃前后只有径向畸变参数发生变化。

4　误差补偿实验与工程应用

4.1误差补偿实验

使用解放军信息工程大学研制的数字摄影测量处理软件DPM，将相机检校后的各类畸变参数作为迭代计算的初值参与平差计算，最终得到对应点的三维坐标值。通过上述分析，将镜头前加设玻璃对像点位移的变化模型归化到镜头径向畸变的数学模型中。为此，可开展以下实验：用镜头前加玻璃和未加玻璃2种情况，分别采集几组数据，计算得到各组之前的坐标转换精度，若数值相当，即可判定利用径向畸变模型可将镜头前加玻璃对像点位移的影响减弱。

为了模拟以上测量条件，将2块普通的玻璃放置在相机的镜头处，用美国GSI公司INCA3相机拍摄2组像片（即E1、E2）；再取下玻璃，拍摄2组像片（即E3、E4）。同上，用佳能5D相机拍摄4组像片（即F1、F2、F3、F4）。

后期用V-Stars软件对有玻璃和无玻璃的2组数据进行处理。其坐标转换精度如表2、表3所示。

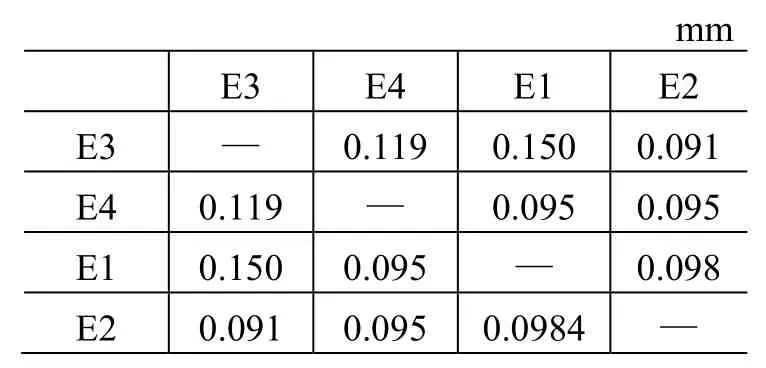
表2　INCA3相机4组数据的坐标转换结果Table 2　Coordinate transformation of INCA3 camera

表3　5D相机4组数据的坐标转换结果Table 3　Coordinate transformation of 5D camera

以上数据表明：镜头前加玻璃，用径向畸变模型可以将玻璃对于像点坐标的影响减弱，以至于对像点的坐标精度几乎无影响。

4.2热真空环境下的工程应用

在长约6m、宽约1.5m的天线面阵前方布设红外加热笼。加热笼为纵向条带式，与天线阵面平行，水平距离为100mm，面积覆盖整个天线阵面。然后在天线表面粘贴摄影标志和安放微晶玻璃基准尺；在红外加热笼达到一定温度（-90～90℃）时，用装进I-CAN罐内的相机和未装进罐内的相机分别测出所有标志点的三维坐标值记为G1、G2组；最后分析2组数据之间坐标转换精度。为了排除实验的偶然性，再重复进行几次实验。

经过数据分析得到高温环境下加保护罐和未加保护罐2种情况的坐标转换精度，如表4所示。

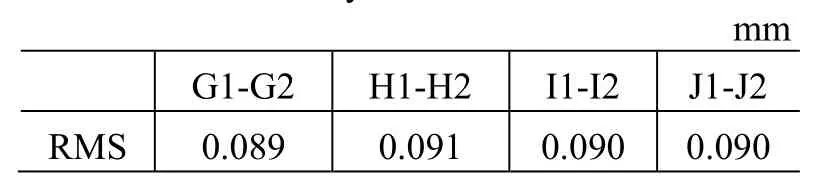
表4　坐标转换精度值Table4　The accuracy of coordinate transformation

最终通过计算可得出像点位移情况，如图7所示。

图7　像点位移矢量图Fig. 7　The graph of displacement vector

通过在热真空模拟环境中的实验数据比对分析可知：加保护罐和不加保护罐这2种状态的转换精度相当。因此，相机加保护罐拍摄对点位坐标测量的精度几乎无影响。

5　结束语

在预设网形条件、相机分辨率、被测物体的尺寸都确定的情况下，镜头处加玻璃对像点坐标的影响只是光的折射的影响。为此设计了镜头处完全覆盖玻璃和不完全覆盖玻璃2类实验，通过对比分析像点坐标变化的位移矢量可以得知：加玻璃后像点坐标变化量最大约为5µm；其位移变化规律与相机径向畸变对像点坐标影响的分布规律相似。而后，通过对镜头处加设不同厚度玻璃的相机检校得知，加设玻璃后各类畸变参数中，只有径向畸变参数发生改变。最后假设将玻璃对坐标测量的影响模型归化到径向畸变模型中，通过2组的误差补偿实验得以验证。在模拟热真空环境下也采集相关数据验证：玻璃对像点坐标测量的影响可以通过径向畸变模型得以减弱。下一步还需要继续从光学的角度深入分析，推导出玻璃折射对像点坐标测量影响的公式。

参考文献（References）

[1] 李晓峰, 汪波, 胡渝. 在轨运行热环境下的天线镜面热变形对空地激光通信链路的影响[J]. 宇航学报, 2005, 26(5): 581-585 Li Xiaofeng, Wang Bo, Hu Yu. Influence of mirror thermal distortion in thermosphere to space-to-ground laser communication links[J]. Journal of Astronautics, 2005, 26(5): 581-585

[2] 黄桂平. 数字近景工业摄影测量关键技术研究与应用[D].天津: 天津大学, 2005

[3] 范生宏. 工业数字摄影测量中人工标志的研究与应用[D].郑州: 解放军信息工程大学, 2006

[4] Bouman J, vanOel J, Muller-Stute F, et al. A photogrammetry system for use in thermal vacuum testing, ESA Bulletin Nr. 81[R], 1995

[5] Wiktowy M, O’Grady M, Atkins G, et al. Photogrammetric distortion measurements of antennas in a thermalvacuum environment[J]. Canadian Aeronautics and Space Journal, 2003(2): 65-71

[6] Ross A. Ka-band transmit reflectors thermal distortion test and correlation[C]∥25thESA Antenna Workshop on Satellite Antenna Technology. Noordwijk, 2002: 395-402

[7] 卢成静. 卫星天线热真空变形测量中工业数字摄影测量技术研究与应用[D]. 郑州: 解放军信息工程大学, 2008

[8] 冯其强. 数字工业摄影测量技术研究与实践[D]. 郑州:解放军信息工程大学, 2010

[9] 程效军. 数字近景摄影测量在工程中的应用研究[D].上海: 同济大学, 2002

（编辑：冯 妍）

Analysis and error compensation of the effect of the protection tank of camera on the photogrammetry accuracy

Cheng Zhiqiang1, Feng Qiqiang1, Yi Wangmin2, Li Zongchun1, Wang Yongqiang1
(1. School of Surveying and Mapping, The PLA Information Engineering University, Zhengzhou, 450001, China; 2. Beijing Institute of Spacecraft Environment Engineering, Beijing 100094, China)

Abstract:The appropriate mathematical model is chosen to reduce the effects on the accuracy by comparing the differences of the displacement distribution before and after applying the glasses. The experiment shows that the protective cover glass of camera has an influence on the measurement accuracy, and the biggest variation of the coordinate of the image point is approximately 5 micrometers and the distribution of the variation consists with the radial distortion. Finally, the influence could be replaced by a radial distortion model and the experiment shows that this method can effectively reduce the effects of the glass on the measurement accuracy.

Key words:vacuum and high-low temperature environment; digital industry photogrammetry; the protection tank of camera; radial distortion; measurement accuracy

作者简介：程志强（1989—），男，硕士研究生，专业方向为精密工程测量。E-mail: 842280711@qq.com。

基金项目：航天器联合测量实验室基金项目资助（CAST-511创新基金）

收稿日期：2015-09-17；修回日期：2016-03-16

DOI：10.3969/j.issn.1673-1379.2016.02.017

中图分类号：P234.1

文献标志码：A

文章编号：1673-1379(2016)-0206-05