尾段主梁刚度变化对T型尾翼颤振特性的影响
2016-05-24张旭王斌
张旭 王斌
(中国航天空气动力技术研究院,北京 100074)
尾段主梁刚度变化对T型尾翼颤振特性的影响
张旭 王斌†
(中国航天空气动力技术研究院,北京 100074)
由于T型尾翼结构和气动布局的特殊性,其颤振特性的分析比较复杂.T型尾翼安装在机身尾部,这体现在有限元结构模型中即为T型尾翼与尾段主梁相连接.为了研究尾段主梁的刚度变化对T型尾翼颤振特性的影响,以某T型尾翼飞机的尾段为研究对象,根据其原始刚度,分别改变其垂直弯曲刚度和扭转刚度,并计算分析相应刚度下的固有振动特性与颤振特性.最后分别以这两个刚度为变量,另一个刚度的原始值为常量进行分析.结果表明尾段主梁的刚度变化对垂尾弯扭耦合颤振的影响较为显著.
T型尾翼, 颤振, 刚度, 主梁, 固有振动
引言
T型尾翼是指将飞机的水平尾翼布置在垂直尾翼翼尖的一种特殊气动布局形式.对于垂尾来说,T型尾翼布局起到了端板效应,提高了垂尾效率,可把垂尾面积减小,弥补了因支撑平尾而加强垂尾带来的重量增加[1].对于平尾来说,在小迎角时,这种布局形式能够避开机翼尾流的影响,同样提高了平尾的气动效率.而在结构方面,这种尾翼结构形式便于后机身的大开口,有利于运输机的货物装运[2].基于这些优点,在很多大型客机和运输机的设计中都采用了T型尾翼.
对于T型尾翼布局,由于结构和外形的特殊性,其颤振特性也较为复杂[3-5].首先在结构方面,由于水平尾翼安置在垂尾的顶部,增加了垂尾在扭转方向的转动惯量,使得垂尾的扭转频率和弯曲频率靠近,导致垂尾弯扭耦合形式的颤振速度降低.同时各部件之间(如平尾与垂尾、垂尾与机身等)的连接刚度对固有振动的频率影响也很大.其次在气动方面,各气动面之间存在很强的气动干扰,尾翼的横向与侧向运动气动耦合严重,也会导致T型尾翼颤振速度的下降[6].
本文将某T型尾翼飞机的尾段作为研究对象,以其结构有限元模型的原始刚度为基础(已经与振动试验结果对比,在前30阶固有振动模态中,除个别模态外,结构有限元模型主要振动模态的频率误差在3%以内),通过分别改变该尾段主梁的垂直弯曲刚度和扭转刚度,计算其颤振特性,最后分析得到,当尾段主梁刚度变化时,可引起部分固有模态发生变化,进而引起T型尾翼的颤振特性发生变化,且具有一定规律.
1 理论基础
1.1 固有振动特性计算
结构固有振动特性计算是在无阻尼结构自由振动的基础上求解结构振动的频率与模态.当把结构离散为有限元素后,其无阻尼自由振动运动方程为:

其中,Ms为结构整体质量矩阵,Ks为结构整体刚度矩阵,x为结点位移列阵.
设x=feiωt,代入(1)式中,得

要使方程(2)中的f有非零解,则

上式称为系统的特征方程,求解特征方程,得到ωi后,再代回(2)式,即可求得特征向量fi.
这里,ωi为固有振动频率,fi为固有振型(模态)[7].通常,根据研究问题的具体需要,只算出结构的前若干阶频率与模态即可.
1.2 非定常气动力计算
T型尾翼颤振分析的特殊性就在于气动力的计算.常规的颤振分析可以利用工程软件来计算非定常气动力.而T型尾翼由于几何外形的特点会导致某种横侧向气动力的耦合,这是常规计算方法没有考虑的,需要采用另外的手段计算气动力的附加部分.
非定常气动力的计算普遍采用基于小扰动线性谐振荡假设的面元法[8].本文中的常规气动力计算采用亚音速偶极子格网法.广义非定常气动力可表示如下[9]:

其中,A0为广义气动力影响系数矩阵.
由于T尾效应产生的附加气动力采用片条理论来计算,根据参考文献[2],附加气动力为:

其中B为片条的气动影响系数矩阵,Φ为模态矩阵.
于是总的T尾非定常气动力可表示为:

1.3 颤振方程与求解
气动弹性运动方程一般写成如下形式[10]:

其中,M为广义质量矩阵,K为广义刚度矩阵,Q为广义非定常气动力列阵.
颤振方程求解的常用方法有V-g法、p-k法等.通过频域求解方法得到一系列频率和阻尼随来流速度的变化信息,由频率耦合趋势和阻尼过零分支的判断可以预测颤振模态和临界颤振速度.由于pk法可以反映一定的亚临界特性,本文采用p-k法进行颤振求解.
2 模型描述
2.1 结构模型
全尾段T型尾翼结构有限元模型主要包括两部分:机身尾段、T型尾翼,如图1所示.后机身由梁单元和集中质量模拟,T型尾翼由垂尾安定面、方向舵、平尾安定面和升降舵组成,方向舵和升降舵分别由多点约束连接到安定面上,并通过操纵杆控制偏转.在整个模型中结构由梁单元组成(图中较粗线条),模拟结构的刚度特性,但不提供质量.在结构结点上布置集中质量(图中的小三角)来模拟结构的质量特性.约束条件为尾段前端固支,即机身重心固支.

图1 T型尾翼尾段结构有限元模型Fig.1 FEmodel of the T-tail
2.2 气动模型
如前所述,本文颤振分析的非定常气动力采用亚音速偶极子格网法(DLM)与片条理论计算得出.气动模型如图2所示.

图2 T型尾翼气动模型Fig.2 Aerodynamic model of the T-tail
3 固有振动特性计算
将尾段前端固支,计算得出全尾段模型的固有振动特性如表1所示(仅列出主要模态).
根据本模型建立时的坐标方向,得知I2(A)即为尾段主梁的垂直弯曲刚度I(yy),而J(A)即为尾段主梁的扭转刚度I(xx)[11].按照相对原始刚度的20%,50%,80%,120%,150%,以其中一个原始刚度为常量,另一个为变量分别改变垂直弯曲刚度I(yy)和扭转刚度I(xx),然后分别计算得出每个相对刚度下的固有振动特性.将结果记录下来进行横向比较发现,随着刚度的提高,固有振动各阶模态的频率升高.在计算的30阶模态中,除个别模态因刚度变化而产生了临近阶次的互换外,其他模态均与原始刚度下得到的固有振动模态大体保持一致.
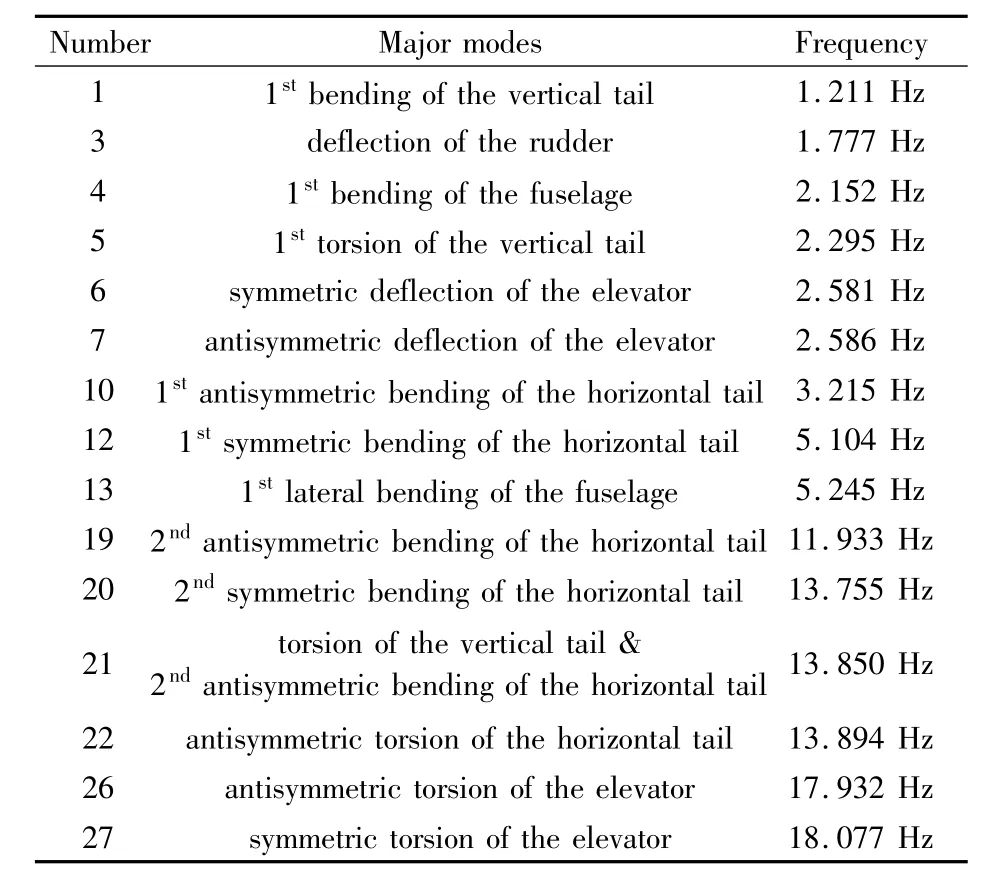
表1 全尾段模型的固有振动特性Table 1 Vibration characteristics of the T-tail
4 颤振特性分析
在全尾段T型尾翼的颤振计算中,飞行高度取为海平面,大气密度ρ=1.225kg/m3,马赫数为0.1,动压为708帕.
4.1 原始刚度下的颤振特性
选取如表1所示的前30阶模态进行计算分析,该模型的颤振结果V-g和V-f曲线如图3和图4所示(注:为了在V-g图和V-f图中显示方便,只画出了其中的主要模态).
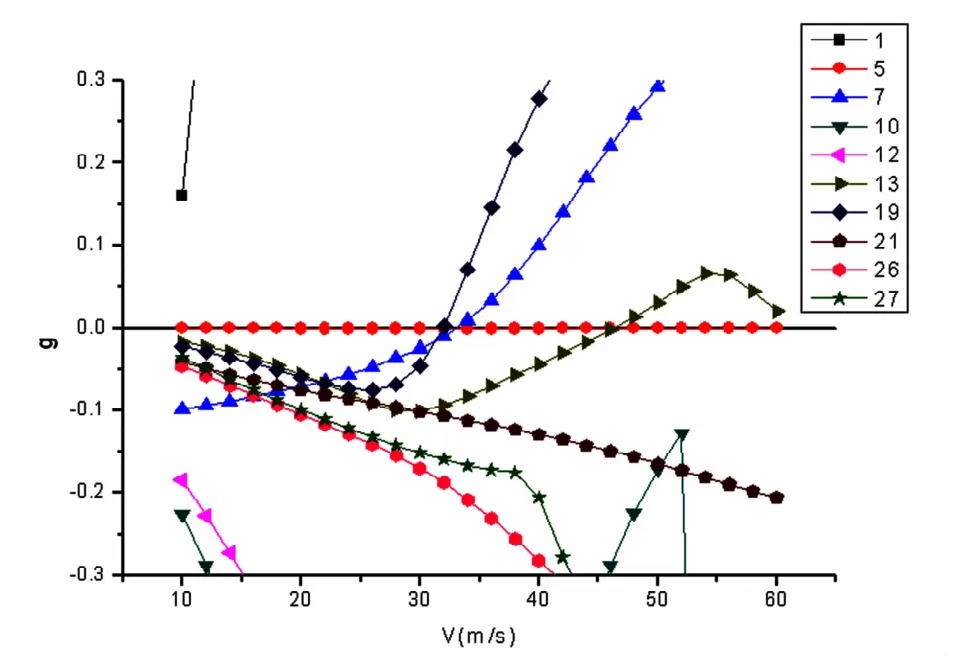
图3 T型尾翼的颤振分析V-g曲线Fig.3 V-g curves of the T-tail
全尾段模型的颤振速度Vf=31.93m/s,颤振频率ωf=8.414Hz,颤振型式为平尾反对称二阶弯曲与平尾反对称扭转耦合(称其为coupling 1).
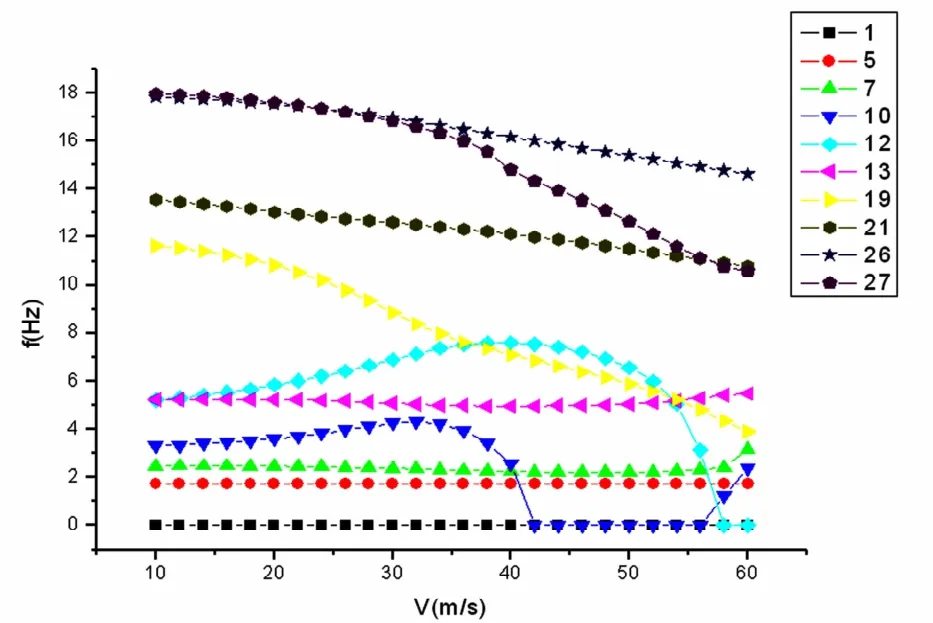
图4 T型尾翼的颤振分析V-f曲线Fig.4 V-f curves of the T-tail
第二穿越点:V=32.98m/s,频率ω=2.338Hz,耦合型式为带有升降舵反偏转的垂尾弯扭耦合(称其为coupling 2).
4.2 改变主梁垂直弯曲刚度后的颤振特性
为了研究尾段主梁的垂直弯曲刚度对T型尾翼颤振特性的影响,与前面固有振动特性的计算相类似,将尾段主梁的垂直弯曲刚度分别改为相对原刚度的20%,50%,80%,120%,150%,然后对这5种相对刚度下的模型进行颤振分析,将结果归纳如图5所示.
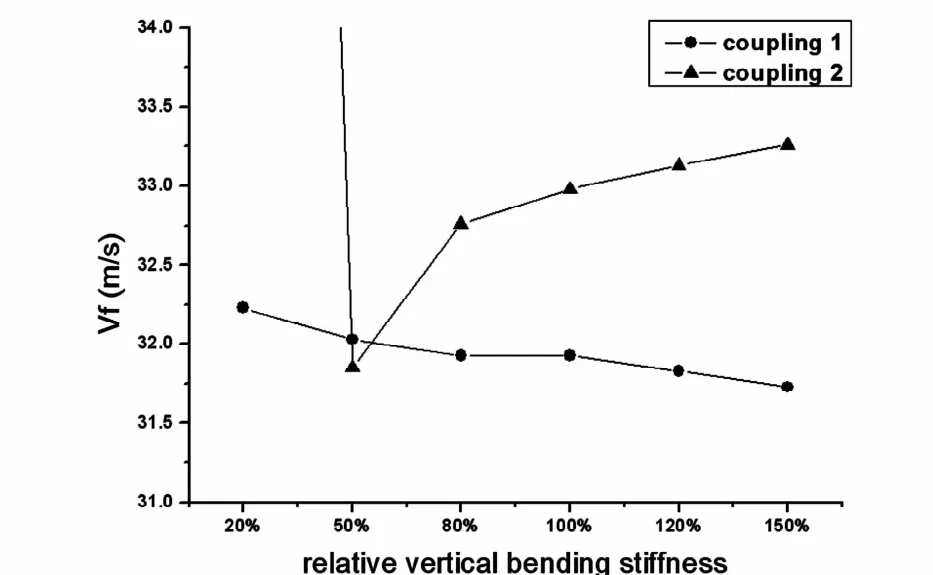
图5 Vf随主梁垂直弯曲刚度变化曲线Fig.5 Flutter speed-vertical bending stiffness relationships of tailmain-beam
4.3 改变主梁扭转刚度后的颤振特性
为了研究尾段主梁的扭转刚度对T型尾翼颤振特性的影响,将尾段主梁的扭转刚度分别改为相对原刚度的20%,50%,80%,120%,150%,然后对这5种相对刚度下的模型进行颤振分析,将结果归纳如图6所示.
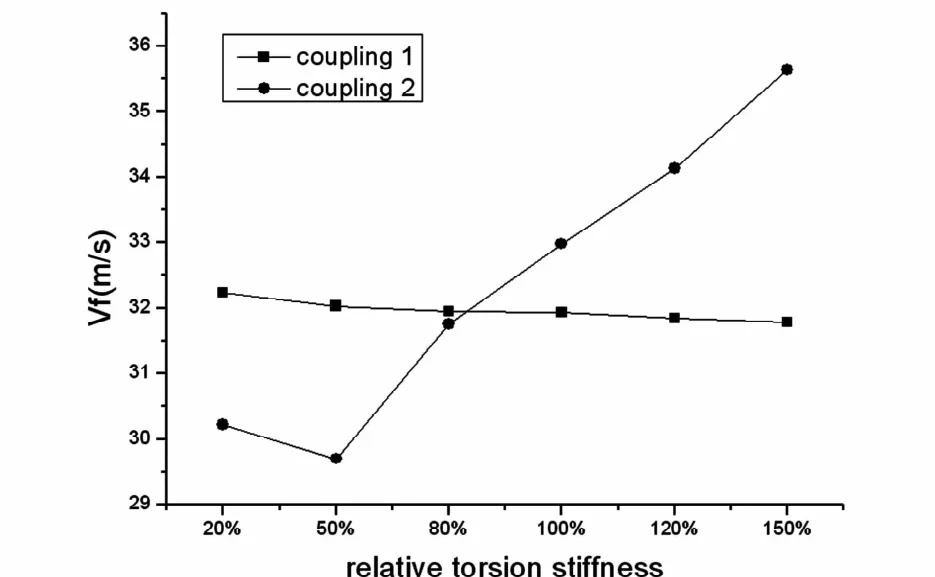
图6 Vf随主梁扭转刚度变化曲线Fig.6 Flutter speed-torsion stiffness relationships of tailmain-beam
4.4 结果与分析
上述两种颤振型式与尾段主梁之间的相互关系如图7所示.

图7 尾段主梁与颤振型式示意图Fig.7 Tailmain-beam and flutter types
由尾段主梁与颤振型式的示意图可知,整个T型尾翼通过垂尾根部与机身尾段主梁连接,尾段主梁的刚度变化将会直接影响垂尾的某些模态.因此可直观推测:尾段主梁刚度变化对垂尾弯扭耦合颤振型(即coupling 2)的影响远大于其对平尾弯扭耦合颤振型(即coupling 1)的影响.
图5、图6的分析结果也恰恰证明了这一点.
1)在平尾反对称二阶弯扭耦合颤振型(coupling 1)中,其颤振速度随相对垂直弯曲刚度的增大而有微小降低.同样,其随相对扭转刚度的增大也有微小降低.
2)在垂尾弯扭耦合颤振型(coupling 2)中,除在20%相对刚度(颤振速度达到51.39m/s)外,其颤振速度随相对垂直弯曲刚度的增大而升高.同样在以原始垂直弯曲刚度为常量,以扭转刚度为变量的分析中,除20%相对刚度时颤振速度稍高外,其随相对扭转刚度的增大而升高.
5 结论
本文以一个T型尾翼飞机的尾段为研究对象,研究尾段主梁的刚度变化对T型尾翼的固有振动特性和颤振特性的影响.通过计算分析得出以下结论:
1)尾段主梁的弯曲刚度变化、扭转刚度变化均对颤振耦合型式1(主要由平尾模态参与耦合)的影响很小;
2)尾段主梁的弯曲刚度变化、扭转刚度变化均对颤振耦合型式2(主要由垂尾模态参与耦合)具有较为显著的影响;
3)尾段主梁刚度是T型尾翼颤振优化设计中不可忽视的关键参数.
1 方宝瑞.飞机气动布局设计.北京:北京工业出版社,1997:462~477(Fang B R.Aerodynamic configuration design of aircraft.Beijing:Aviation Industry Publishing Company,1997:462~477(in Chinese))
2 吕斌,吴志刚,杨超.T型尾翼颤振特性分析方法.工程力学,2008,25(2):230~234(Lv B,Wu Z G,Yang C.Analysis of T-tail flutter.Engineering Mechanics,2008,25(2):230~234(in Chinese))
3 Cbarles L R,Maynard C S.Experimental parametric studies of transonic T-tail flutter,NASA TN D-8066,1975
4 Rodden W P.Commenton“Effectofstabilizer dihedral and static lift on T-tail flutter”.Journal of Aircraft,1978,15(7):447~448
5 Land N S,Fox A G.An experimental investigation of the effects of mach number,stabilizer dihedral,and fin torsional stiffness on the transonic flutter characteristics of a Tee-tail,NASA TN D-924,1961
6 JenningsW P,Berry M A.Effectof stabilizer dihedral and static lift on T-tails flutter.Journal of Aircraft,1977,14(4):364~367
7 王尚文,余旭东.飞行器结构动力学.西安:西北工业大学出版社,1986:97~112(Wang SW,Yu X D.Structural dynamics of aircraft.Xi′an:Northwestern Polytechnical University Press,1986:97~112(in Chinese))
8 谌胜,刘春川,李凤明.基于CFD/CSD方法的亚音速平板结构气动弹性分析.动力学与控制学报,2013,11(4):363~368(Shen S,Liu CC,Li FM.Aeroelastic analysis of plate structures in subsonic air flow based on CFD/CSD algorithm.Journal of Dynamics and Control,2013,11(4):363~368(in Chinese))
9 管德.飞机气动弹性力学手册.北京:航空工业出版社,1994:126~139(Guan D.Aircraftaeroelastic dynamic handbook.Beijing:Aviation Industry Publishing Company,1994:126~139(in Chinese))
10 陈桂彬,邹丛青,杨超.气动弹性设计基础.北京:北京航空航天大学出版社,2004(Chen G B,Zou CQ,Yang C.Elements of Aeroelastic dynamics.Beijing:Beijing U-niversity of Aeronautics and Astronautics Press,2004(in Chinese))
11 Kevin K.MSC/NASTRAN quick reference guide.U.S.A:The MacNeal-Schwendler Corporation,1997:921~927
EFFECT OF STIFFNESS VARIATION OF TAIL MAIN-BEAM ON FLUTTER CHARACTERISTICSOF T-TAIL
Zhang Xu Wang Bin†
(China Academy of Aerospace Aerodynamics,Beijing100074,China)
Analysis on the flutter characteristics of T-tails is complicated because of their special structure and aerodynamic configuration.The T-empennage is fixed on the afterbody,and in a structure finite elementmodel,this can be represented by connecting the T-tails and themain beam.To study the influences of stiffness variations of tailmain-beam on flutter characteristics,the empennage of a T-tail aircraft is studied according to its original stiffness,considering the change of vertical bending stiffness and torsional stiffness.And the corresponding characteristics of natural vibration and flutter are analyzed.Finally,the flutter characteristics ofmodelswith two variable of above stiffness(vertical bending stiffness and torsional stiffness)and one constantof the original value of either stiffness are analyzed.The results demonstrate that the influences of stiffness variations of tailmain-beam on bending-torsion-coupled flutter of vertical tail are significant.
T-tails, flutter, stiffness, main-beam, natural vibration
10.6052/1672-6553-2016-22
2016-1-18收到第1稿,2016-3-11收到修改稿.
†通讯作者E-mail:caaawb@163.com
Received 18 January 2016,revised 11 March 2016.
†Corresponding author E-mail:caaawb@163.com
