NSGA-Ⅱ在克拉玛依市水资源优化配置应用初探
2016-05-23李承红
李承红,何 英
(新疆农业大学 水利与土木工程学院,新疆 乌鲁木齐 830052)
NSGA-Ⅱ在克拉玛依市水资源优化配置应用初探
李承红,何英
(新疆农业大学 水利与土木工程学院,新疆 乌鲁木齐 830052)
[摘要]在经济、社会不断发展的今天,水资源供需矛盾在克拉玛依市白杨河流域显得尤为突出。基于多目标遗传算法原理与水资源可持续发展理论,针对克拉玛依市的供水关系、水资源特征以及水资源开发利用现状,将遗传算法、多目标优化问题和Pareto非劣解集理论相结合,建立克拉玛依市水资源多目标优化配置模型;通过一系列满足不同条件的解集,选择出在不同环境条件下的可适用的方案。结果表明,通过NSGA-Ⅱ遗传算法的计算,达到经济效益最大化,并且缺水量最小,具有较好的优化效果,结果合理可靠,可为克拉玛依未来城市规划和发展提供依据。
[关键词]克拉玛依市;水资源;NSGA-Ⅱ; 多目标优化
由于水资源的不合理利用以及社会经济不断地发展,造成克拉玛依市水资源供需矛盾日益突出。因此,进行克拉玛依市水资源优化配置研究,有利于克拉玛依市的工业发展 、建筑业发展以及农业的协调发展,有利于人与自然地和谐相处,有利于水资源的可持续利用。
水资源的优化配置涉及因素多、用户多、水源多、目标多等,是一个结构复杂的大系统,具有多目标,多层次,多要求,非线性等特点,传统的方法已经不能很好的解决大系统多目标的问题。近几年,采用智能算法,如神经网络[1]、模拟退火算法[3-5]、遗传算法[6-9]等研究切削用量选择和优化的方法很多。研究方法主要有:将多目标问题取单目标极值作为研究结132果,或者将多目标问题通过加权等方法转发为单目标问题,再求取最优解,不能反映同时满足多目标条件下,侧重某一条件下的取值问题。Kalyanmoy Deb 带精英策略的快速非支配排序遗传算法(nondominated sorting genetic algorithm Ⅱ,NSGA-Ⅱ)是运用最为广泛最成功的一种[10]。实践证明,NSGA-Ⅱ多目标优化算法具有全局搜索性、大规模处理、较高的通用性、并行性以及一次可以得到多个Pareto最优解等特性,能够有效的克服传统多目标优化算法的局限性[11-12],并且避免了早熟收敛。
本研究基于多目标遗传算法原理与水资源可持续发展理论,针对克拉玛依市的供水关系、水资源特征以及水资源开发利用现状,结合水资源优化配置原则、克拉玛依市相关规划[13],采用智能控制遗传算法、多目标优化问题与Pareto非劣解集理论相结合进行目标优化,构建水资源多目标优化配置模型;该模型可获得一系列满足不同条件的解集,提供了在不同环境条件下的多种灵活可选择的方案,可为克拉玛依市水资源可持续利用和规划管理提供理论依据。
1克拉玛依市水资源现状
克拉玛依市地处准噶尔盆地西北边缘。地理介于东经84°44′~86°01′和北纬45°20′~46°08′之间,属于大陆性气候,克拉玛依市年均降水量116 mm,年蒸发量平均在2 958 mm(Ф20 cm蒸发皿),干旱少雨,蒸发量大,东邻准噶尔盆地的古尔班通古特沙漠,北和塔城地区的和布克赛尔蒙古自治县相接,西与塔城地区托里县为邻,西南与乌苏县,东南与克拉玛依市玛纳斯河流域区和沙湾县相连,总面积4 683 km2(全市面积7 733.9 km2),城市建成区面积32.87 km2。2011年,白杨河流域地表水可利用量41 707万 m3,地下水可利用量2 828万 m3。
2水资源优化配置模型
充分考虑克拉玛依市的水资源系统的特点,选取经济发展、社会发展作为目标,建立克拉玛依市水资源优化配置模型。水资源优化配置的一般模型为[14]:
Z=max{f1(x),f2(x)}
G(x)≤0
(1)
x≥0
式中:f1(x),f2(x)为 经济目标、社会目标。G(x)为约束条件;x为决策变量。
2.1决策变量
克拉玛依市水源主要为:地表水、地下水、中水,考虑克拉玛依市是一座以工业发展为主的工业城市,将用水用户分为工业用水、建筑用水、服务业用水、农林用水、生活用水、生态用水,其中将生态补水和艾里克湖用水共同计入生态用水,根据克拉玛依市实际发展情况,在设置决策变量时应充分考虑中水使用情况,中水不得用于生活用水。(见表1)
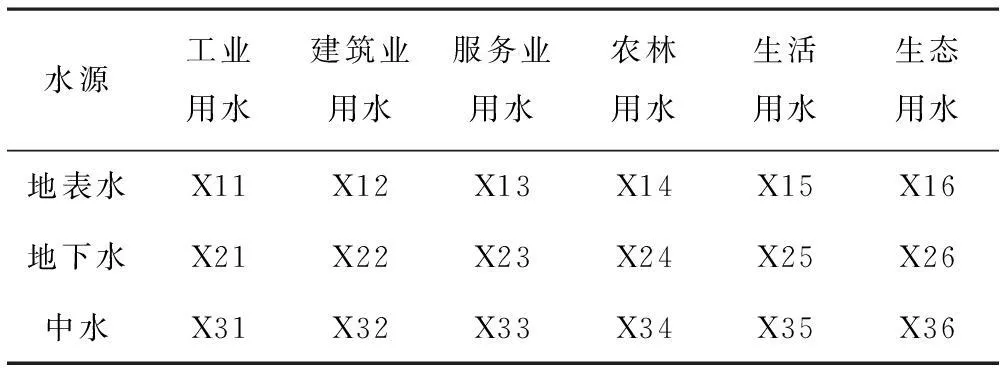
表1 克拉玛依市决策变量选取
2.2目标函数
1) 经济目标,以供水效益最大来表示
式中:xij为水源i向用户j的供水量(108m3);bij为效益系数(元/m3);cij为费用系数(元/m3);αi为供水系数;βj为用户公平系数。
2) 社会目标,社会目标不宜度量,需要建立具体的指标来表示,水资源优化配置的最终目的是来解决水资源的短缺与水竞争的问题,克拉玛依市缺水量越少,各行业发展情况越好,社会经济效益越高,因此选择克拉玛依市的社会效益采用缺水量最少。
式中:Dj为用户j的需水量(108m3)
2.3约束条件
1) 水库的供需水量平衡方程
式中:Wi为i水源的可供水量(108m3)
2) 区域用户从水源地获得水量应该位于用户需水量上下限之间
式中:kHj为j用户需水量上线;kLj为j用户需水量下线
本研究中生活用水、工业用水、建筑业用水、农林用水、服务业用水、生态用水等取各自需水量作为上限,生活用水的下限取需水量的97%,工业用水的下限取需水量的90%,建筑业用水的下限取需水量的90%,服务业用水的下限取需水量的95%,农林用水的下限取需水量的80%,生态用水的下限取需水量的80%。
3) 非负性
xij≥0
2.4模型参数确定
1)效益系数bij
效益系数:农林用水、工业用水、建筑业用水和服务业用水效益系数采用农林业万元产值、工业万元产值、建筑业万元产值和服务业万元产值用水量的倒数计算[15-16]:
bij=10 000/Q
式中:Q为农林业万元产值、工业万元产值、建筑业万元产值和服务业万元产值用水量
生活用水和环境用水的效益受经济因素和社会因素等多方面因素的影响,造成生活用水和环境用水的效益难以估计,为了突出生活用水和环境用水的效益的重要性,这里取各用户用水效益的最大值的一半。
2)费用系数Cj
参考水费增收标准确定,若缺乏资料,参考邻近水源工程[16]。
农林业用水费用为0.01元/m3、工业、建筑业用水费用为2.46元/m3、服务业用水费用为0.25元/m3,生活用水费用为1.93元/m3,生态环境用水费用为0.92元/m3。
3)供水次序系数kαi以及用水公平系数kβj
供水次序系数αi:反映水源相对于其他水源有限供水程度
用水公平系数βj:反映j用户相对于其他用户先得到供水的重要性
式中:ni为i水源供水次序序号;nmax为水源供水次序序号最大值。
遵循水资源优化配置公平性、有效性。可持续性以及优先性原则,按照现生活后生产、地表水多水源联合供水的原则,按照先生活后生产,地表水水源优先、尽量减少地下水的开采、多种水源联合配置、统筹规划等安排,确定水源供水先后次序为地表水、地下水、中水。考虑到克拉玛依市经济社会的发展,将工业用水次序仅次于生活用水,其用户的供水次序为生活、工业用水、建筑业用水、农林用水、服务业用水、生态用水。计算供水次序系数依次为0.5,0.33,0.17;用户公平系数分0.33,0.27,0.27,0.2,0.13,0.07。
3模型求解
3.1多目标优化及pareto最优解问题可以描述如下[10]
min[f1(x),f2(x),…,fm(x)]
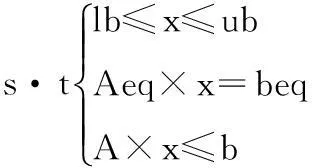
(1)
其中:fi(x) 为待优化的目标函数;x 为待优化的变量;lb和ub分别为变量 x 的下限和上限的约束;Aeq×x=beq为变量的线性等式约束;A×x≤b为变量的线性不等式约束。

图1 gamultiobj函数调用
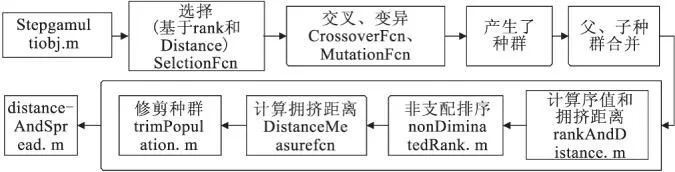
图2 函数stepgamultiobj结构
3.2gamultiobj组织结构
函数gamultiobj基于遗传算法,个体(individual),适应度函数(fitness function)和适应度函数值(fitness value),种群(population)和种群大小(population size),选择(selection),交叉(crossover),变异(mutation)等与GA均相同,多目标优化函数gamultiobj的调用步骤图1所示。
3.3函数stepgamultiobj分析(见图2)
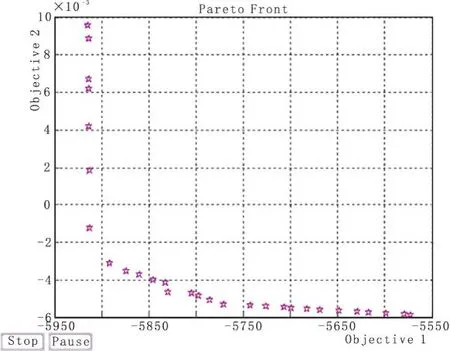
图3 第一前端个体分布图
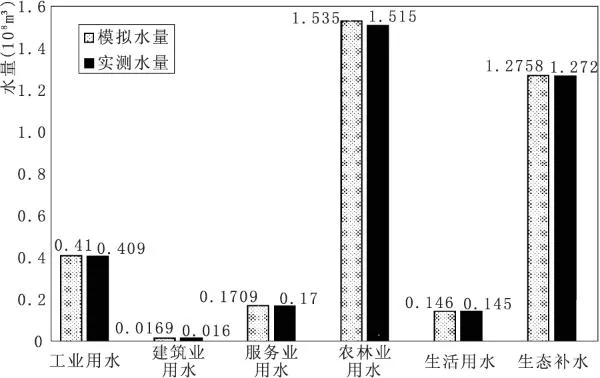
图4 克拉玛依市水资源优化结果对照图
(108 m3)
注:1)总水量为水资源优化配置后的结果;2)实际毛耗水量为克拉玛依市规划报告实际调查数据;3)缺水量为实际毛耗水量与总水量的差值,结果为负,表明有余水。
3.4结果分析
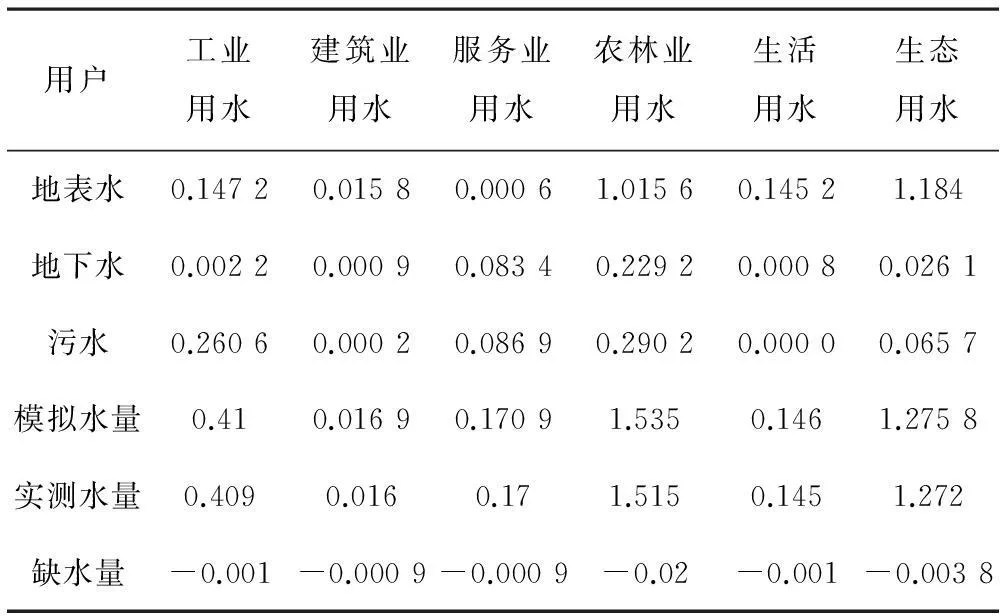
根据2011年克拉玛依市用水量统计情况进行gamuliobj函数的校核,通过模型计算,最大经济效益5.813亿元,各个用户缺水量为零,分析结果见表2,第一前端个体分布图见图3,克拉玛依市水资源优化结果对照表见图4。计算结果与2011年克拉玛依市实际用水情况相符。采用此方法对对克拉玛依市2020年,2030年水资源进行水资源配置。2020年克拉玛依市水资源高、中情景配置结果以及2030年克拉玛依市水资源高、中情景配置结果见表3,图5。
由克拉玛依市优化模型解得,2011年克拉玛依市生活实际毛用水量为0.145×108m3,模型结果为0.146×108m3,余水量为0.001×108m3;工业实际毛用水量为0.409×108m3,模型结果为0.41×108m3,余水量为0.001×108m3;建筑业实际毛用水量为0.016×108m3,模型结果为0.0169×108m3,余水量为0.000 9×108m3;农林实际毛用水量为1.515×108m3,模型结果为1.535×108m3,余水量为0.02×108m3;服务业实际毛用水量为0.17×108m3,模型结果为0.170 9×108m3,余水量为0.000 9×108m3;生态实际毛用水量为1.272×108m3,模型结果为1.275 8×108m3,余水量为0.003 8×108m3。

表3 克拉玛依市不同水平水资源配置结果
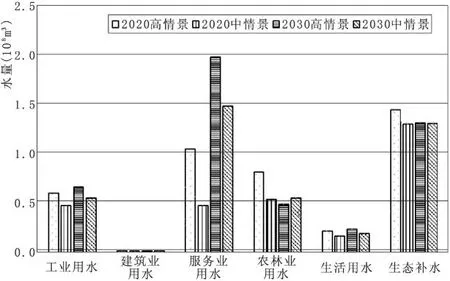
图5 克拉玛依市不同水平水资源配置结果
4结语
函数gamultiobj的调用,通过2011年实际用水与NSGA-Ⅱ遗传算法比较,克拉玛依市水资源优化模型能够真实地反映克拉玛依市实际水资源系统用水情况,表明NSGA-Ⅱ遗传算法在水资源优化配置中的应用效果较好,优化结果可靠。
克拉玛依市资源可供水量有限,水资源优化配置实在需水量上下限之间,并没有完全满足各个用户的用水要求,供需矛盾依旧突出,节水以及污水回用在未来的经济发展仍然是重要任务。
参考文献
[1]赵韩,冯宝林,董晓慧,等.基于改进的BP神经网络对切削参数的优化选择[J].机床与液压.2008,36(5):213-215.
[2]吕明珠,刘世勋. 模拟退火算法在电磁兼容领域的应用[J].盐城工学院学报:自然科学版.2014,03:22-25.
[3]王战平. 宁夏引黄灌区水资源优化配置研究[D].宁夏:宁夏大学.2014.
[4]韩啸,刘淑芬,徐天琦. 基于遗传模拟退火算法的改进K-medoids算法[J]. 吉林大学学报:工学版.2015,02:619-623.
[5]孔珊珊,李秀霞. 基于模拟退火粒子群优化的恒模算法[J].通信技术.2015,01:32-36.
[6]黄曼丽,等.基于遗传算法的区域水资源优化配置研究[J].人民长江.2008,39(06);29-32.
[7]N. Lerma , J. Paredes-Arquiola , J. Andreu & A. Solera.Development of operating rules for a complex multi-reservoir system by coupling genetic algorithms and network optimization[J]. Hydrological Sciences Journal, 2013, 58(4): 796-812.
[8]Mohammad Karamouz , Mahmoud M.Rezapour Tabari & Reza Kerachian . Application of Genetic Algorithms and Artificial Neural Networks in Conjunctive Use of Surface and Groundwater Resources[J]. Water International, 2007, 32(1): 163-176.
[9]高佳,赵本龙,索惠霞. 馆陶县水资源优化配置研究[J]. 海河水利.2008,13( 4) :7-9.
[10]史峰,王辉. MATLAB智能算法30案列分析[M].北京:北京航天航空大学出版社.2011.89-101.
[11]肖小伟,肖迪,林锦国,等. 多目标优化问题的研究概述[J].计算机应用研究.2011,28(3):805-808.
[12]付涛,王大镇,弓清忠,等. 基于改进型BP神经网络和NSGA-Ⅱ遗传算法的机械零件多目标优化[J].组合机床与自动化加工技术.2013,0.9,39-41.
[13]姜卉芳. 克拉玛依水资源有配置研究报告[R]. 新疆: 新疆农业大学.2011.
[14]张志军,黄宝连.基于水资源优化配置的多目标决策模型探析[J].水利规划与设计.2010,12:18-21.
[15]郝真. 山东省水资源优化配置研究[D].山东:山东师范大学.2011.
[16]张家凤. 开都河—孔雀河流域水资源优化配置研究[D].乌鲁木齐:新疆农业大学.2012.
The NSGA - Ⅱ Application Optimization Allocation of Water Resources in Karamay
LI Cheng-hong,HEying
(Xinjiang Agricultural University,Urumqi 830052, Xinjiang)
Abstract:With the development of social economy,the contradiction between supply and demand of water resources is becoming more and more prominent in Karamay Baiyanghe River. The paper is based on multi-objective genetic algorithm principle and the sustainable development of water resources theory, the light of the regional water supply of Karamay relations, the characteristics of water resources ,the water resources development and utilization of the status quo,using genetic algorithm and intelligent control of multiobjective optimization problems with Pareto non inferior solution set theory combining objective optimization,establishes a multi-objective optimal allocation model of water resources.The model can meet the needs of different conditions to obtain a series of solutions,provides various in different conditions of flexible alternatives. Results show that through the calculation of the NSGA - Ⅱ genetic algorithm, to maximum the economic benefits and the minimum amount of water, with better optimization results, the result is reasonable and reliable, can provide the basis for future urban planning and development Karamay.
Key words:Karamay;Water resources;The NSGA -Ⅱ;Multi-objective optimization
[中图分类号]TV211.1
[文献标识码]A
[文章编号]1004-1184(2016)02-0126-04
[作者简介]李承红(1988-),女,新疆库尔勒人,在读硕士研究生,主攻方向:水文学及水资源。[通讯作者]何英(1982-),女,新疆乌鲁木齐人,副教授,博士,研究方向:水文学及水资源。
[收稿日期]2015-11-16
