压力机成本-公差模型及质量损失模型研究

陈启升，李爱香，曹 奇，别世清，尤锡龙

（山东恒宇重工机械有限公司，山东 高密 261500）

压力机成本-公差模型及质量损失模型研究

陈启升，李爱香，曹 奇，别世清，尤锡龙

（山东恒宇重工机械有限公司，山东 高密 261500）

本文以压力机的公差与配合为研究对象，运用数学函数方法，在满足装配目标的情况下，主要研究了指数模型、改进的指数模型、负平方模型、倒数幂指数模型、多项式模型和复合模型的各种形式，以及三种质量损失函数。对压力机尺寸链中各组成环的公差进行合理分配，以达到降低成本之目的。

压力机；公差；函数模型；配合；成本

加工成本是压力机总成本的重要组成部分，它是体现企业经济的主要标志，而影响机械加工成本的诸多因素中零部件的公差影响最大，且公差是产品设计和制造的重要技术条件。以成本最低为目标，展开了成本－公差的建模技术研究[1－3]。

1 成本-公差模型

压力机公差分配是公差设计的重要组成部分，其主要研究是指在满足装配目标的情况下，对尺寸链中各组成环的公差进行合理的分配，并且尽量符合经济性原则。国内外相关研究人员对公差分配问题关注一直非常多，且相关研究成果也非常多，但是使用基于优化技术的公差分配方法求解公差分配问题，并给出最优解的却不多。本文将用最优化理论解决公差分配问题，下面将先介绍几种常见的加工成本函数模型。

1.1 指数加工成本函数模型

指数模型（Exponential Model）：

式中：t为设计公差；C（t）为加工成本；a、b、c为已知参数，且a>0、b>0、c>0。

假如在一个线性尺寸链中有n个组成环，设第i个组成环的公差用ti（i=1，2，…，n）表示，并且每个组成环的尺寸公差加工成本都符合式（1），设第i个组成环的加工成本函数表示为：

式中：ai、bi、ci为大于零的已知参数，其中i=1，2，…，n。

则在这个线性尺寸链中，各组成环的加工成本总和函数表示为：

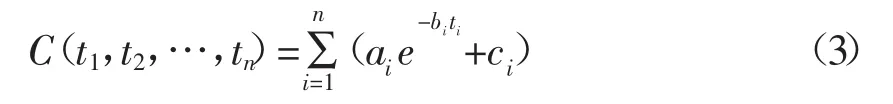
式中：ai、bi、ci为大于零的已知参数，其中i=1，2，…，n。

1.2 改进的指数加工成本函数模型

改进的指数模型（Modified Exponential Model）：

式中：t为设计公差；C（t）为加工成本；a、b、d及m为已知参数，且a>0、b>0。

假如在一个线性尺寸链中有n个组成环，设第i个组成环的公差用ti（i=1，2，…，n）表示，并且每个组成环的尺寸公差加工成本都符合式（4），设第i个组成环的加工成本函数表示为：

式中：ai、bi、di、及mi为大于零的已知参数，其中i=1，2，…，n。

则在这个线性尺寸链中，各组成环的加工成本总和函数表示为：

式中：ai、bi、di、及mi为大于零的已知参数，其中i=1，2，…，n。

1.3 负平方加工成本函数模型

负平方模型（Reciprocal Squarel Model）：

式中：t为设计公差；C（t）为加工成本；a、b为已知参数，且 a>0、b>0。

假如在一个线性尺寸链中有 n个组成环，设第i个组成环的公差用ti（i=1，2，…，n）表示，并且每个组成环的尺寸公差加工成本都符合式（7），设第i个组成环的加工成本函数表示为：

式中：ai、bi为大于零的已知参数，其中i=1，2，…，n。

则在这个线性尺寸链中，各组成环的加工成本总和函数表示为：

式中：ai、bi为大于零的已知参数，其中i=1，2，…，n。

1.4 倒数幂指数加工成本函数模型

倒数幂指数模型（Reciprocal powers Model）：

式中：t为设计公差；C（t）为加工成本；a、b为已知参数，且 a>0、b>0。

假如在一个线性尺寸链中有 n个组成环，设第i个组成环的公差用ti（i=1，2，…，n）表示，并且每个组成环的尺寸公差加工成本都符合式（10），设第 i个组成环的加工成本函数表示为：

式中：ai、bi为大于零的已知参数，其中i=1，2，…，n。

则在这个线性尺寸链中，各组成环的加工成本总和函数表示为：

式中：ai、bi为大于零的已知参数，其中i=1，2，…，n。

1.5 多项式加工成本函数模型

多项式模型（Polynomial Model），例如三次多项式模型为：

式中：t为设计公差；C（t）为加工成本；a0、a1、a2和a3为已知参数，且a0>0、a1>0、a2>0、a3>0。

假如在一个线性尺寸链中有 n个组成环，设第i个组成环的公差用ti（i=1，2，…，n）表示，并且每个组成环的尺寸公差加工成本都符合式（13），设第 i个组成环的加工成本函数表示为：

式中：a0i、a1i、a2i和a3i为大于零的已知参数，其中i=1，2，…，n。

则在这个线性尺寸链中，各组成环的加工成本总和函数表示为：

式中：a0i、a1i、a2i和a3i为大于零的已知参数，其中i=1，2，…，n。

多项式模型有多种，如四次多项式模型、五次多项式模型等等，这里主要以三次多项式模型为例子进行分析。

1.6 复合加工成本函数模型

复合模型（Hybrid Model），常用到的复合模型有指数和幂指数混合模型、线性和指数混合模型、指数和分式混合模型、指数和倒指数混合模型、倒指数积和指数混合模型等。

1.6.1 指数和幂指数混合模型

式中：t为设计公差；C（t）为加工成本；a0、a1、a2、a3和a4为已知参数，且a0>0、a1>0、a2>0、a3>0、a4>0。

假如在一个线性尺寸链中有 n个组成环，设第i个组成环的公差用ti（i=1，2，…，n）表示，并且每个组成环的尺寸公差加工成本都符合式（16），设第i个组成环的加工成本函数表示为：

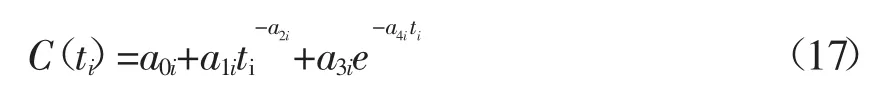
式中：a0i、a1i、a2i、a3i和a4i为大于零的已知参数，其中i=1，2，…，n。

则在这个线性尺寸链中，各组成环的加工成本总和函数表示为：

式中：a0i、a1i、a2i、a3i和a4i为大于零的已知参数，其中i=1，2，…，n。

1.6.2 线性和指数混合模型

式中：t为设计公差；C（t）为加工成本；a0、a1、a2和a3为已知参数，且 a0>0、a1>0、a2>0、a3>0。

假如在一个线性尺寸链中有n个组成环，设第 i个组成环的公差用ti（i=1，2，…，n）表示，并且每个组成环的尺寸公差加工成本都符合式（19），设第i个组成环的加工成本函数表示为：

式中：a0i、a1i、a2i和a3i为大于零的已知参数，其中i=1，2，…，n。

则在这个线性尺寸链中，各组成环的加工成本总和函数表示为：

式中：a0i、a1i、a2i和a3i为大于零的已知参数，其中i=1，2，…，n。

1.6.3 指数和分式混合模型

式中：t为设计公差；C（t）为加工成本；a0、a1、a2和a3为已知参数，且a0>0、a1>0、a2>0、a3>0。

假如在一个线性尺寸链中有n个组成环，设第 i个组成环的公差用ti（i=1，2，…，n）表示，并且每个组成环的尺寸公差加工成本都符合式（22），设第i个组成环的加工成本函数表示为：

式中：a0i、a1i、a2i和a3i为大于零的已知参数，其中i=1，2，…，n。

则在这个线性尺寸链中，各组成环的加工成本总和函数表示为：

式中：a0i、a1i、a2i和a3i为大于零的已知参数，其中i=1，2，…，n。

1.6.4 指数和倒指数混合模型

式中：t为设计公差；C（t）为加工成本；a0、a1、a2和a3为已知参数，且a0>0、a1>0、a2>0、a3>0。

假如在一个线性尺寸链中有n个组成环，设第i个组成环的公差用ti（i=1，2，…，n）表示，并且每个组成环的尺寸公差加工成本都符合式（25），设第i个组成环的加工成本函数表示为：

式中：a0i、a1i、a2i和a3i为大于零的已知参数，其中i=1，2，…，n。

则在这个线性尺寸链中，各组成环的加工成本总和函数表示为：

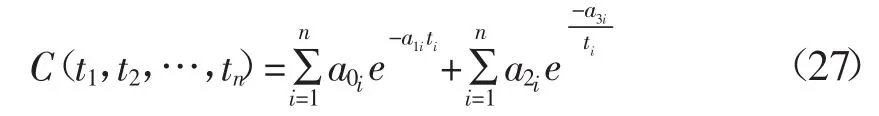
式中：a0i、a1i、a2i和a3i为大于零的已知参数，其中i=1，2，…，n。

1.6.5 倒指数积和指数混合模型

式中：t为设计公差；C（t）为加工成本；a0、a1、a2和a3为已知参数，且a0>0、a1>0、a2>0、a3>0。

假如在一个线性尺寸链中有n个组成环，设第i个组成环的公差用ti（i=1，2，…，n）表示，并且每个组成环的尺寸公差加工成本都符合式（28），设第i个组成环的加工成本函数表示为：

式中：a0i、a1i、a2i和a3i为大于零的已知参数，其中i=1，2，…，n。

则在这个线性尺寸链中，各组成环的加工成本总和函数表示为：

式中：a0i、a1i、a2i和a3i为大于零的已知参数，其中i=1，2，…，n。

这些模型的共同点是：在某一个特定的加工环境中，统计大量的公差与加工成本数据，再用最小二乘法等方法求出模型中的相关参数，得到的拟合曲线一般情况下是单调递减的，且是非线性关系，统计模型越复杂，得到的相关数据精度就越高，但拟合难度就越大。

2 质量损失模型

公差是体现产品质量的重要标志，公差的大小对产品质量和生产成本都有着非常大的影响，是平衡产品质量与生产成本之间的关键因素[4，5]。传统的质量观只把重点放在了如何设计结构和生产制造上，而忽略了公差概念的缺陷，实质上是一种被动式、服从式的质量观，对于这种质量观的公差只用了两个极值进行描述，称为传统公差或二值公差，如图1所示。按照这种观念，压力机的质量只需考虑公差是否在这两个极值内，如果在就认为是合格的，而忽略了零部件公差偏离目标值的大小。

图1 二值公差

一般情况下，公差值的大小离目标值越近就说明质量越好，而不是传统质量观认为的只要在公差极值范围内就是合格的，当实际的公差值偏离目标值越多，产品质量损失就越大，因此，压力机公差值的大小不仅要看是否在规定的范围内，而且也要看实际值偏离目标值的大小程度，要把产品的质量看成是连续的变量。显而易见，传统的公差概念是不能做到这一点的，所以，日本学者田口玄一博士提出了质量损失的概念，这种观念强调产品对客户造成的损失也是质量损失，这种观念是一种主动式、现代式质量观。对于这种质量观的公差我们需要对产品的生产实际公差值进行统计，然后再进行描述，因此又叫做统计公差，如图2所示。所以，在这种观点的基础上评价一个产品质量的优劣，不仅要看公差是否在规定的极限范围内，同时也要看公差值偏离目标值的大小程度，对于用户来说偏离的越大质量越是不好，比较注重产品的质量损失，即公差值偏离目标值的大小程度，但是质量损失越小也会导致加工成本越高。

图2 统计公差

质量特性偏离质量设计目标值的大小是引起质量损失和质量问题的主要原因，因此田口玄一博士建立了质量损失函数，用质量损失函数来表达质量损失与质量特性波动之间的关系。质量损失QL（Quality Loss）是质量特性值x的函数。不同的产品质量特性对应着不同的产品质量损失曲线，当产品公差值偏离目标值越小，产品质量越好，偏离目标值越大，产品质量越差，当产品公差值正好等于目标值时，也就是说产品质量损失为零。但是，产品的公差值只要在规定的范围内，我们就认为产品是合格的，也是可靠的，只不过是生产过程中尽量向目标值靠近，把质量损失降到最低，公差值只要在规定的范围内就不会再考虑偏离目标值的程度。

为了让产品的质量损失能进行量化比较，需要对质量损失进行定义，因而田口玄一博士建立了质量损失函数概念。他把产品的质量特征值设为x，目标值设为m，当x等于m时，产品的质量损失最小，即质量损失为零，当x与d不相等时，x与m相差的绝对值越大，质量特征离目标值越远，即产品的质量损失越大。用L（x）来表示质量特征x所对应的质量损失，设L（x）在x等于m处存在高阶导数，根据泰勒展开公式得出以下公式：

根据上述假定和公式，当x=m时，L（x）=0，则求出L（m）=0；同时，由于L（x）在x=m处有最小值，可知L′（m）=0。忽略掉二阶以上的高阶项，那么质量损失函数近似表示为：

田口先生认为质量损失是由于质量特性值x偏离设计目标值所引起的，有所偏离，就会有所损失，根据质量特征x的目标值m的取值不同，质量损失函数可以分为以下三种不同的情况。

2.1 望目特性的质量损失函数

望目特征的质量损失函数是指质量特征x与目标值m之间的偏差大小与经济损失多少之间的关系函数，设质量特征x的目标值为m，质量特性值x在目标值m左右波动，波动越小质量越好，则x就被称为望目特性，尺寸公差多属于此类型的质量特征，如图3所示。比如某轴件加工尺寸为ø5±0.02（mm），目标值为m=5（mm），实际加工尺寸x就属于望目特性。质量损失函数的表达式为：

由公式（33）可以看出，质量特性值x的波动所造成的质量损失与质量特性值x偏离目标值m的偏差平方成正比，也就是说，产品不合格会造成损失，即使产品合格同样会造成一定的损失，质量特性值x偏离目标值m越远，造成的损失越大。这就是日本学者田口玄一博士提出来的关于质量的新观点，把这种二次方程用作质量损失函数，从中我们可以看到很多相关信息。从图3所示的曲线可知，质量损失函数是连续的二次函数曲线，质量特性值x在规定的公差范围内并不一定表示该产品质量优良，最优的产品质量是该产品的质量特性值x稳定在该产品的目标值m上，该曲线就更形象地展示了关于质量的新观点。传统的质量观点是一种不连续的阶跃函数，只要质量特性值 xL在规定的公差范围内就没有损失，只有当质量特性值x超出规定的公差范围极限才算有质量损失。

图3 望目特性

下面介绍两种K值的确定方法：

（1）由功能界限Δ0和产品丧失功能后的损失A0求K，功能界限Δ0是指产品的功能是否能正常发挥的临界值，A0是指产品丧失功能之后的损失。当｜xm｜≤Δ0时，产品的功能能正常发挥，当｜x-m｜＞Δ0时，产品丧失功能。把产品丧失功能之后的损失A0代入式（33）可得：

（2）由容差Δ和产品不合格后的损失A求K，容差Δ是判定产品是否合格的临界值。当｜x-m｜≤Δ时，产品为合格品，当｜x-m｜＞Δ时，产品为不合格品。当产品不合格时，对该产品可以采取报废或是返修等措施，但是这样造成的损失记为A元。代入式（33）可得：

2.2 望小特性的质量损失函数

望小特性是指质量特性值x不取负值，质量特性值x越小越好，波动越小越好，则x被就称为望小特性。如图4所示，比如实际测量的误差值、形位公差、表面粗糙度等就属于望小特性。质量损失函数的表达式为：

图4 望小特性

2.3 望大特性的质量损失函数

图5 望大特性

望大特性是指质量特性值x不取负值，质量特性值x越大越好，波动越小越好，则x就被称为望大特性。如图5所示，比如企业的利润、压力机的使用寿命等就属于望大特性。质量损失函数的表达式为：

3 小结

本文研究了压力机成本-公差模型的各种模型与质量损失模型的各种模型。成本-公差模型主要研究了指数模型、改进的指数模型、负平方模型、倒数幂指数模型、多项式模型和复合模型的各种形式。质量损失模型是基于田口先生的质量观，主要研究了望目特性的质量损失函数、望小特性的质量损失函数和望大特性的质量损失函数。

[1]刘玉生，吴昭同，杨将新.基于成本模型的计算机辅助公差优化设计的研究[J].浙江大学学报（自然科学版），1995，29（6）：698-705.

[2]杨将新，吴昭同.机械加工成本-公差建模技术的研究[J].浙江大学学报（自然科学版），1996，30（5）：517-522.

[3]邵锦文，张振家，冯国泰.基于一种新的公差成本模型的工艺优化设计[J].航天制造技术，2002，（2）：8-11.

[4]方红芳，何 勇，吴昭同.基于田口质量观的并行公差设计的研究[J].机械设计，1998，（3）：22-25.

[5]黄美发，钟艳如.基于制造成本与质量损失的并行公差设计[J].现代制造工程，2004，（5）：68-70.

Study on cost-tolerance model and quality loss model of press

CHEN Qisheng,LI Aixiang,CAO Qi,BIE Shiqing,YOU Xilong
（Shandong Hengyu Heavy Industry Machinery Co.,Ltd.,Gaomi 261500,Shandong China）

Taking the tolerance and fit of press as the research object in the text,in order to meet the assembly target,the mathematical function method has been adopted to study various form of exponential model, modified exponential model,negative square model,inverse power exponent model,and polynomial model& mixed model,as well as three kinds of quality loss function.The tolerance of each ring in the dimension chain of the press has been reasonably allocated,in order to reduce the cost.

Press;Tolerance;Fit;Cost;Function model

TG305

A

10.16316/j.issn.1672－0121.2016.04.034

1672－0121（2016）04－0116－05

2016－02－19；

2016－04－07

陈启升（1965－），男，高级工程师，从事机械压力机开发设计。E－mail：chqsh2012＠163.com