柔性多体系统动力学的并行迭代算法

孙 卫, 周小平

(1. 西京学院 应用统计与理学系, 陕西 西安 710123; 2. 四川师范大学 数学与软件科学学院, 四川 成都 61006)

柔性多体系统动力学的并行迭代算法

孙 卫1, 周小平2

(1. 西京学院 应用统计与理学系, 陕西 西安 710123; 2. 四川师范大学 数学与软件科学学院, 四川 成都 61006)

为了提高多体系统动力学数值计算的稳定性和精度，针对柔性多体系统动力学建模方式和求解算法问题，采用分类算法、迭加算法完成了柔性多体系统动力学模型求解，利用波形松弛技术和RK离散方法设计并实现了柔性多体系统的并行迭代算法，为了降低计算的复杂性改进这些迭代算法的收敛速度，提出了内外步并行迭代进程，并进一步证明了相应迭代算法的收敛性，完成了误差估计.

柔性; 多体系统; 波形松弛; 并行进程; 优化

多体系统动力学的研究核心任务是高精度地求解在外力作用下系统整体动力学行为,将多体系统动力学问题模型化,对该系统进行数值分析求解.由于多体系统的相互耦合及位形空间的位数增大,导致多体动力学方程产生严重的刚性问题且维数增多,如何提高数值计算的稳定性和精度是多体系统动力学数值解法的重要课题[1-3]，亦是本文研究工作的目的.

随着机械工程、航天技术应用复杂程度日益增加,多刚体系统模型无法考虑柔性体的变形动力耦合效应,更能真实地反映实际系统动力行为的柔性多体动力学应运而生.时至今日柔性多体系统动力学已成为计算力学领域的重要发展方向,各种新兴的研究方法层出不穷,建模和数值计算难题探讨越发显现其重要性[4-6].由于柔性系统是具有无限多个自由度的连续模型,其动力学方程通常为维数十分庞大的微分-代数混合方程组,只能用各种离散方法求出其近似解.为提高动力学方程的数值计算精度和稳定性,近年来出现了一系列改进的计算策略,然而微分-代数方程的求解仍是多体系统动力学与控制中的一个难点[7-9],仍无非常通用和程式化的方法.

针对上述难题,将波形松弛技术应用于柔性多体系统演化方程的计算剖分中,对数值计算的数据进行采集解耦处理,采用分步算法、迭加算法完成方程的并行迭代;同时考虑到隐式Runge-Kutta方法具有单步方法的固有优点,特别是具有处理刚性问题所必备的稳定性和高精度，所以选用隐式Runge-Kutta方法完成模型的时间域离散.

基于上述迭代技术和离散方法,设计了基于柔性多体系统演化方程RK离散的波形松弛迭代技术并行进程,关于修正牛顿(modified Newton)法的内外步并行迭代进程,论证了通过降低计算的复杂性可以改进这些迭代算法的收敛速度.对于内外步迭代算法证明了算法的收敛性,并分别做了相应的误差估计.

1 柔性多体系统动力学程式化模型的实现

由于系统部件大范围运动和构件本身变形的相互耦合作用,给柔性多体系统动力学建模与分析计算带来了许多困难.基于不同建模方法得到的多体系统动力学方程形式不尽相同,运动方程可以写在许多不同的方式,其中之一是著名的Lagrange方程第一形式[1,7]

(1)

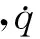
dC(t,q)=G(t,q)dq+b(t,q)dt=0

成立.在定常约束条件下,非完整约束方程形式为

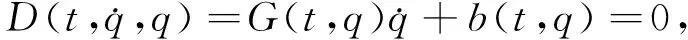
亦为速度极约束.

基于完整约束的Lagrange模式为非线性微分-代数方程,由表达式(1)和运动约束C(t,q)=0组成

(2)

若广义质量阵M(t,q)∈Rnq×nq和约束阵G(t,q)∈Rnλ×nq满秩,方程(2)为指标-3微分-代数方程.完整约束C(t,q)=0对t求二阶微分

ψ=-(Ctt(t,q)+2Ctq(t,q)z+Cqq(t,q)z2),

设初始条件为ψ(t0,z0,q0)=0,z0=z(t0),q0=q(t0),当且仅当矩阵G满秩时方程(2)有唯一解.

(3)

其中,qn和zn分别是q(tn-1+cih)和z(tn-1+cih)在网格点tn处的近似值,⊗为Kronecker乘积,I为s×s单位阵,A为nq×nq矩阵,向量b、d、e是nq维向量,且满足条件

(d1,…,dnq)=(b1,…,bnq)A-1.

2 隐式RUNGE-KUTTA迭代进程

为了求解微分方程(2)考虑动力学迭代或波形松弛技术.波形松弛技术作为一类重要的解耦算法具有内在并行性的优势,使实际系统灵活选择适合的迭代算法,波形松弛方法的实现可以根本地改进数值方法的稳定性能,迭代技术具体实现形式为

其中q(0)(·)和z(0)(·)是给出的初始猜测函数,在时间域[t0,tT]上假设q(0)(·)≡q0和z(0)(·)≡z0.剖分后的函数φ:φ(t,u,u,v,v)=φ(t,u,v),矩阵

波形松弛技术最大的优点是将复杂的系统解耦,子系统由不耦合或弱耦合的组成并保持着原系统的某些特性,进行并行处理时可节省大量运算时间,当系数矩阵为髙度稀疏矩阵,适宜用计算机计算.

基于迭代技术和离散方法设计了针对柔性多体系统演化方程的波形松弛迭代技术的RK离散并行进程,关于修正牛顿(modified Newton)法的内外步并行迭代进程.

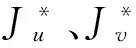
fork=1 tomPar-do;

forn=κω+1 to (κ+1)ωPar-do;

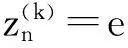
set

end for;

end for.

(5)

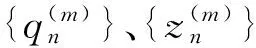
2.2 修正Newton法的内外步迭代进程 考虑Waveform Newton迭代法,求解strongly非线性难题时该迭代法收敛条件弱且速度较快,只需迭代几次就能达到原问题的解所要求的精度.应用IRK离散后的迭代张量形式为

(6)

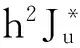
forj=1tomPar-do

forv=1torPar-do;

set

endfor;

endfor.

(7)

分解矩阵

i,j=1,…,s

共有σ块对角子阵(矩阵B为下三角实阵),则矩阵N0算法复杂度O(sσp-1(m*)3).

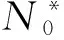
3 收敛分析

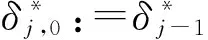
综合迭代张量形式(6)和内外步迭代过程(7)得

上式也可表示为误差的递推式

(8)

其中

v=1,…,r.

进一步地分析内外步迭代序列的收敛性,给出下列的广义特征方程

(9)

其中λ是方程的特征值，设μ和b⊗ω分别是矩阵M的特征值和特征向量,则M(b⊗ω)=μ(b⊗ω)成立,即有下列的特征方程成立

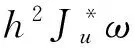
(10)

定义z:=λh2并将广义特征方程(9)式代入(10)式,得到

z(A-B)(b⊗ω)=μ(I-zB)(b⊗ω). (11)

若ω≠0成立,则矩阵

z(z):=z(I-zB)-1(A-B)

的特征值为μ=μ(z),其中I-zB非奇异;对于大多数IRK矩阵A来说,满足下列条件的对角及下三角阵B存在:当Re(z)≤0时矩阵z(z)的特征值μ(z)在单位圆里.

如果矩阵B拥有上面的特性,定义矩阵集B(A)，与矩阵A有关.

定义 1 设

z(z):=z(I-zB)-1(A-B).

(12)

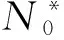
(13)

成立,其中j=1,…,m.更进一步地,记

H(Δ):=-(A⊗I)[Φ(qn+Δ)-Φ(qn)]+

(14)

综合(8)、(13)和(14)式,可以得到误差递推式

由IRK数值离散张量形式(6)可得迭代差推导式

当稳态函数R(∞)满足‖R(∞)‖≤1时,IRK张量式(6)是A-stable.类似地有下面结论.

4 数值算例分析

通过一非线性微分-代数方程算例验证上述的系列离散并行迭代算法.设非线性微分-代数方程的形式如下

(15)

方程的波形松弛迭代形式如下

其中常数满足A=A1+A2,B=B1+B2,D=D1+D2.对方程的波形松弛迭代式(15)利用四阶LobattoIIIARK法进行离散,并分别用波形松弛迭代并行算法(5)和内外步迭代并行算法(7)在网格实验室4个节点并行机上完成该数值算例的运算.设步长h,并行算法(5)的迭代次数k和内外步迭代次数r、m是固定的.

定义记号εzG,εzI,εqG,εqI具体如下:

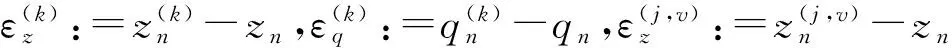
通过比较表1(εzG波动松弛/εzI内外部迭代)和表2(εqG波动松弛/εqI内外部迭代)中并行迭代算法运算误差结果可以看到:内外步迭代并行算法(7)的并行迭代模式效能是优于波形松弛迭代并行算法(5).

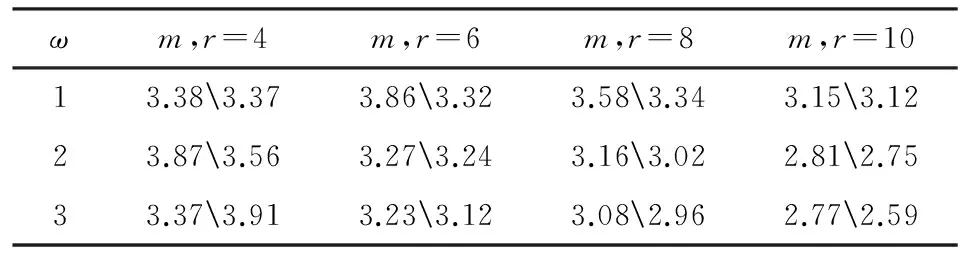
表 1 z值运算误差

表 2 q值运算误差

5 结语

对于完整约束下的柔性多体运动系统动力学模型，提出了隐式Runge-Kutta数值离散张量形式,实现了基于波形松弛迭代技术、修正Newton法内外步并行迭代进程，这些迭代算法具有在并行机上运行的适用性，可以实时模拟和求解复杂的机械系统问题，并适用于现有的多体系统动力学仿真软件的实现.

对系统使用波形松弛迭代法时也存在着效率较低、收敛慢的主要缺点,为了改善迭代算法的收敛性能,采用Krylov子空间预处理技术来改进并行迭代算法的收敛速度,并使用当前并行算法设计主流的粗粒度构造并行算法,以增强软件的维护性和可移植性.最后针对一个非线性微分-代数算例具体地测试这些迭代算法的实用有效性,在多粒度的并行程序设计和实现时有多种平台支持,本算例选择性能较好的MPI+OpenMP应用编程接口作为并行计算平台.

[1] ARCZEWSKI K, BLAJER W, FRACZEK J, et al. Multibody Dynamics: Computational Methods and Applications[M]. New York:Springer-Verlag,2012:135-148.

[2] 王琪,庄方方,郭易圆,等. 非光滑多体系统动力学数值算法的研究进展[J]. 力学进展,2013,43(1):101-111.

[3] 李伟东,胡永明,韩小强,等. 基于多体动力学递推算法的电动汽车建模与仿真分析[J]. 计算力学学报,2012,29(3):357-362.

[4] 戎保,芮筱亭,王国平,等. 多体系统动力学研究进展[J]. 振动与冲击,2011,30(7):178-187.

[5] SHABANA A A. Dynamics of Multibody Systems[M]. 3rd Rev. Cambridge:Cambridge University Press,2010:112-130.

[6] BAUCHAU O A. Flexible Multibody Dynamics[M]. New York:Springer-Verlag,2011:146-186.

[7] 丁洁玉,潘振宽. 多体系统动力学微分-代数方程广义:α投影法[J]. 工程力学,2013,30(4):380-384.

[8] 徐自然,吴明儿. 弹性杆刚性体系统动力学分析的广义逆矩阵方法[J]. 计算力学学报,2013,30(S):74-78.

[9] 吴锋,高强,钟万勰. 刚-柔体动力学方程的保辛摄动迭代法[J]. 应用数学和力学,2014,35(4):341-352.

[10] NIELSEN M B, KRENK S. Conservative integration of rigid body motion by quaternion parameters with implicit constraints[J]. International Journal for Numerical Methods in Engineering,2012,92(8):734-752.

[11] POURSINA M, ANDERSON K S. An extended divide-and-conquer algorithm for a generalized class of multibody constraints[J]. Multibody System Dynamics,2013,29(3):235-254.

[12] CRITCHLEY J H, ANDERSON K S. A parallel logarithmic order algorithm for general multibody system dynamics[J]. Multibody System Dynamics,2004,12(1):75-93.

[13] 崔蔚,曾宪雯,赵国伟. 线性方程组正交化行处理法并行算法[J]. 四川师范大学学报(自然科学版),2004,27(5):492-496.

[14] 贡玉军,何中全,牛森. 一类广义非线性多值变分包含的迭代算法[J]. 广西师范学院学报(自然科学版),2008,70(2):16-20.

[15] YOO W S, KIM K N, KIM H W, et al. Development of multibody system dynamics: computer simulations and experiments[J]. Multibody System Dynamics,2007,18:35-58.

[16] TIAN Q, ZHANG Y Q, CHEN L P, et al. Dynamics of spatial flexible multibody systems with clearance and lubricated spherical joints[J]. Computers & Structures,2009,87(13/14):913-929.

[17] ZHANG C J, DU S Y, LIU J, et al. Robust iterative closest point algorithm with bounded rotation angle for 2D registration[J]. Neurocomputing,2016,195:172-180.

[18] XU J H. An iterative algorithm for computing mean first passage times of Markov chains[J]. Applied Mathematics and Computation,2015,250(2):372-389.

[19] POPOVICIU L. Parallel iterative algotitjm for solving poisson’s equation[C]//Proceedings of the Scientific Conference. AFASES,2013:371-374.

[20] MARTIN G, LUKAS K, JONAS T, et al. On the parallel iterative solution of linear systems arising in the FEAST algorithm for computing inner eigenvalues[J]. Parallel Computing,2015,49:153-163.

[21] 阚子云,彭海军,陈飙松,等. 开放式多体系统动力学仿真算法软件研发(II)DAEs求解算法对比[J]. 计算力学学报,2015,32(6):707-715,721.

[22] 李安志,任继念,崔蔚. 三对角方程组通用性迭代解法[J]. 四川师范大学学报(自然科学版),2013,36(1):57-60.

[23] 马秀腾,翟彦博,罗书强. 多体系统动力学仿真向后微分公式算法[J]. 计算机集成制造系统,2013,19(1):119-126.

[24] 万波,江晓涛. 求解多值广义混合隐似平衡问题的迭代算法[J]. 四川师范大学学报(自然科学版),2011,34(2):197-200.

2010 MSC：65L05

(编辑 周 俊)

Parallel Iterative Algorithm Studies of Flexible Multibody System Dynamics

SUN Wei1, ZHOU Xiaoping2

( 1. Department of Applied Statistics and Science, Xijing College, Xi’an 710123, Shaanxi; 2. College of Mathematics and Software Science, Sichuan Normal University, Chengdu 610066, Sichuan

In order to improve the stability and accuracy of multibody system dynamics calculation, the paper focuses on the modeling and algorithm for flexible multibody system dynamics. By using classification algorithm and iterative algorithm, the flexible multibody system dynamics model is solved. The parallel iterative algorithm is accomplished by the waveform relaxation technique and the Runge-Kutta method. In order to reduce the complexity of the calculation and improve the convergence speed of the iterative algorithm, the inner-outer step parallel iterative process has been proposed, and the convergence of the iterative algorithm is further proved, and the error estimate has been accomplished as well.

flexible; multibody system; waveform relaxation; parallel process; optimization

2015-12-13

国家自然科学基金(11371289)和陕西省自然科学基础研究计划项目(2016JM1032)

孙 卫(1964—),副教授,主要从事非线性系统算法的研究,E-mail:smsunwei@163.com

O193

A

1001-8395(2016)06-0869-06

10.3969/j.issn.1001-8395.2016.06.018