具有奇异振动外力项的非自治修正Swift-Hohenberg方程一致吸引子的一致有界性和收敛性

刘世芳, 马巧珍

(西北师范大学 数学与统计学院, 甘肃 兰州 730070)

具有奇异振动外力项的非自治修正Swift-Hohenberg方程一致吸引子的一致有界性和收敛性

刘世芳, 马巧珍*

(西北师范大学 数学与统计学院, 甘肃 兰州 730070)

考虑当ρ∈[0,1)和ε>0时,具有奇异振动外力项的非自治修正Swift-Hohenberg(S-H)方程

ut+△2u+2△u+au+b|u|2+u3=g(x,t)+ε-ρh(t/ε),

和相应的ε=0时的S-H方程

ut+△2u+2△u+au+b|u|2+u3=g(x,t),

修正的Swift-Hohenberg方程; 一致吸引子; 奇异振动外力项; 一致有界

令ρ∈[0,1)和ε>0,考虑如下具有奇异振动外力项的非自治修正Swift-Hohenberg方程

ut+△2u+2△u+au+b|u|2+u3=

g(x,t)+ε-ρh(t/ε), (x,t)∈Ω×[τ,∞),

u(x,τ)=uτ(x),x∈Ω,

(1)

在方程(1)中,若ε=0,则方程变为

ut+△2u+2△u+au+b|u|2+u3=

g(x,t), (x,t)∈Ω×[τ,∞),

u(x,τ)=uτ(x),x∈Ω.

(2)

Swift-Hohenberg方程是文献[1]在研究对流流体动力学、环形等离子体约束装置和粘性流时提出来的,在文献[2-4]中也有相关介绍.近年来,动力系统的长时间行为吸引了许多学者和专家的关注.文献[5]研究了系统(2)当g≡0时全局吸引子的存在性.文献[6]进一步给出了K次可微函数空间HK(Ω)中全局吸引子的存在性.最近,文献[7]研究了系统(2)拉回吸引子的存在性;文献[8]研究了系统(2)一致吸引子的存在性.

本文主要研究带有奇异振动外力项系统(1)的一致吸引子的一致有界性和当ε→0+时方程(1)的吸引子与系统(2)的吸引子之间的关系.运用文献[9]中的方法,证明方程(1)的一致吸引子Aε如下的一些性质:

‖

1 预备知识

(3)

(4)

关于φ∈Hω(φ0)一致.

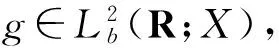
K={u(·)|U(t,τ)u(τ)=u(t),

dist(u(t),u(τ))≤Cu,∀t≥τ,τ∈R}.

集合K(s)={u(s)|u(·)∈K}被称作是在时刻t=s(s∈R)的核截片.

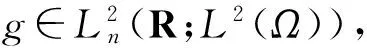
AΣ=ω0,Σ(B0)=ωτ,Σ(B0), ∀τ∈R.

进一步,可得由方程(2)生成的过程族{Uσ(t,τ)}σ∈Hω(g)是弱连续的.

⇀Uσ0(t,τ)uτ, ∀t≥τ.

∀S∈R.

(5)

2 主要结果及证明

vt+△2v+2△v+av=

h(t/ε),v|t=τ=0

(6)

的解,其中ε∈(0,1],且满足不等式

‖△v(t)‖2≤Cε.

(7)

证明 用△2v与(6)式在L2(Ω)上作内积可得

(h(t/ε),△2v(t))-(2△v(t),△2v(t)).

结合Hölder和Young不等式得

‖△v(t)‖2+α1‖△v(t)‖2≤‖(h(t/ε)‖2,

其中α1=2a-4>0.根据Gronwall引理可知

事实上,v(τ)=0.

vt+△2v+2△v+av=

ε-ρh(t/ε),v|t=τ=0.

(8)

类似定理2.1有

‖△v(t)‖2≤Cε1-ρ, ∀t≥τ.

(9)

令w(t)=u(t)-v(t),则w(t)满足方程

wt+△2w+2△w+aw+b|u|2+u3=

g(x,t),w|t=τ=uτ.

(10)

用w与(10)式作内积可得

‖w(t)‖2+‖△w(t)‖2=

-(b|(w(t)+v(t))|2,w(t))-

((w(t)+v(t))3,w(t))+(g(x,t),w(t))+

由(a+b)2≤2(a2+b2)与(a+b)3≤4(a3+b3)得

‖w(t)‖2+2‖△w(t)‖2≤

4|b|(|w(t)|2+|v(t)|2,w(t))+

8(w(t)3+v(t)3,w(t))+2(g(x,t),w(t))+

(11)

在Gagliardo-Nirenberg不等式[7]中,取k=1,n=p=r=m=q=2,θ=1/2可得

4‖w(t)‖2≤c‖△w(t)‖‖w(t)‖≤

其中,c是任意的正常数.

在Gagliardo-Nirenberg不等式中,取k=1,n=2,p=4,r=4,m=q=2,0<θ<1/2,结合Hölder和Young不等式有

(4|b||w(t)|2,w(t))≤

4|b|‖‖w(t)‖≤

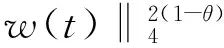
将上述估计代入(11)式,结合Hölder、Young和Poincaré不等式可得

在Gagliardo-Nirenberg不等式中,取k=1,p=4,n=m=q=r=2,θ=1/4,结合Young不等式可得

16|b|2‖‖v(t)‖3‖△v(t)‖≤

在Gagliardo-Nirenberg不等式中,取k=0,p=6,n=m=q=r=2,θ=1/6,结合Young不等式可得

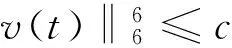
再结合Poincaré不等式得

其中β=λ/2.结合(9)式有

‖w(t)‖2+β‖w(t)‖2≤

其中Cλ是关于λ的常数.根据Gronwall引理可知

‖w(t)‖2≤Ce-β(t-τ)‖uτ‖2+

(12)

用△2w与(10)式作内积,结合Young不等式可得

-2a‖△w(t)‖2+16‖△w(t)‖2+

16|b|2‖‖

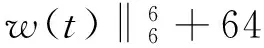
类似前面的讨论得

‖△w(t)‖2+γ‖△w(t)‖2≤

c‖w(t)‖6+c‖w(t)‖10+‖△v(t)‖2+

c‖v(t)‖6+c‖v(t)‖10+4‖g(t)‖2,

进一步,由(9)和(12)式有

‖△w(t)‖2+γ‖△w(t)‖2≤

cR3+cR5+Cε1-ρ+Cλ(ε3(1-ρ)+ε5(1-ρ))+

其中

根据Gronwall引理可知

‖△w(t)‖2≤Ce-γ(t-τ)‖△uτ‖2+

由u=w+v和(9)式可得

‖△u(t)‖2≤Ce-γ(t-τ)‖△uτ‖2+

(13)

因此,过程族Uε(t,τ)有一个不依赖于ε的吸收集B*.由于Aε⊂B*,则定理得证.

为了证明定理2.3,首先需要比较当初始值相同时,分别取ε>0和ε=0时,相应的方程(1)的解.记

uε(t)=U(t,τ)uτ,

其中uτ属于吸收集B*.由(13)式可得一致估计

(14)

特别地,当ε=0时,由于uτ∈B*,则有

(15)

其中R0=R0(ρ),因为B*的大小依赖于ρ.

引理 2.4 对∀ε∈(0,1],τ∈R和∀uτ∈B*,误差

w(t)=uε(t)-u0(t),

其中uε(0)=u0(0)=uτ,对任意的不依赖于ε的常数C,满足估计

证明 由于误差w(t)是方程

wt+△2w+2△w+aw+b|uε|2+

(uε)3-b|u0|2-(u0)3=

ε-ρh(t/ε),w|t=τ=0, ∀t≥τ

(16)

的解.

令q(t)=w(t)-v(t),其中v(t)是方程(6)的解,则q(t)满足Cauchy问题

qt+△2q+2△q+aq+b|uε|2+

(uε)3-b|u0|2-(u0)3=0,

q|t=τ=0.

(17)

用△2q与(17)式在L2(Ω)上作内积可得

‖△q(t)‖2+2‖△2q(t)‖2≤

-2a‖△q(t)‖2+(4△q(t),△2q(t))+

2(|b||u0(t)|2,△2q(t))+

2((u0(t))3,△2q(t))+

2(|b||uε(t)|2,△2q(t))+

2((uε(t))3,△2q(t)).

由Hölder和Young不等式得

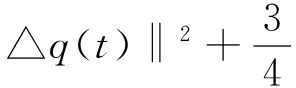
(2a-16)‖△q(t)‖2≤

4|b|2‖‖

4|b|2‖‖

‖△q(t)‖2+R2‖△q(t)‖2≤C(‖△u0(t)‖2+‖△u0(t)‖6+‖△u0(t)‖10+

‖△uε(t)‖2+‖△uε(t)‖6+‖△uε(t)‖10),

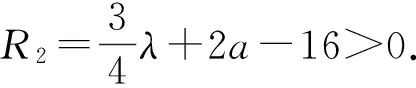
由(14)和(15)式,根据Gronwall引理可知

由w(t)=q(t)+v(t)和(9)式可得

为了研究一致吸引子的收敛性,需要引理2.4更一般的形式,其对应的方程为

(18)

对任意的ε∈[0,1],令

引理 2.5 如下不等式成立

其中,C、R0、R1和R2是引理2.4中所提到的.

且

当t=0和τ=-L时,结合引理2.5可得

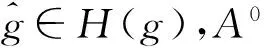
令L=T,结合上述2个不等式,可得

因此,由于uε∈Aε是任意的,则有

其中δ>0是任意的常数,证毕.

[1] SWIFT J B, HOHENBERG P C. Hydrodynamic fluctuations at the convective instability[J]. Phys Rev,1977,A15(1):319-328.

[2] PELETIER L A, ROTTSCHFER V. Large time behaviour of solutions of the Swift-Hohenberg equation[J]. CR Acad Sci Paris Serl,2003,336:225-230.

[3] PELETIER L A, ROTTSCHFER V. Pattern selection of solutions of the Swift-Hohenberg equation[J]. Physica,2004,D194(1):95-126.

[4] PELETIER L A, WILLIAMS J F. Some canonical bifurcations in the Swift-Hohenberg equation[J]. SIAM J Appl Dyn Syst,2007,6(1):208-235.

[5] POLAT M. Global attractor for a modified Swift-Hohenberg equation[J]. Comput Math Appl,2009,57(1):62-66.

[6] SONG L, ZHANG Y, MA T. Global attractor of a modified Swift-Hohenberg equation inHkspaces[J]. Nonlinear Anal:TMA,2010,72(1):183-191.

[7] PARK S H, PARK J Y. Pullback attractor for a non-autonomous modified Swift-Hohenberg equation[J]. Comput Math Appl,2014,67(3):542-548.

[8] XU L, MA Q Z. Existence of the uniform attractors for a nonautonomous modified Swift-Hohenberg equation[J]. Adv Diff Eqns,2015,2015(1).DOI:10.1186/s13662-015-0492-9.

[9] ANHA C T, TOANB N D. Nonclassical diffusion equations on RNwith singularly oscillating external forces[J]. Appl Math Lett,2014,38:20-26.

[10] LU S S, WU H Q, ZHONG C K. Attractors for nonautonomous 2D Navier-Stokes equations with normal external forces[J]. Discr Cont Dyn Syst,2005,13(3):701-719.

[11] CHEPYZHOV V V, VISHIK M I. Attractors for Equations of Mathematical Physics[M]. Providence:Am Math Soc,2002.

[12] 周彪. 非线性时滞系统的一致有界性[J]. 四川师范大学学报(自然科学版),2000,23(1):33-35.

[13] 李惠,蒲志林,陈光淦. 非自治吊桥方程的一致吸引子及其维数估计[J]. 四川师范大学学报(自然科学版),2009,32(5):557-563.

[14] VISHIK M I, PATA V, CHEPYZHOV V V. Time averaging of global attractors of nonautonomous wave equations with singularly oscillating external forces[J]. Dokl Akad Nauk,2008,78(2):689-692.

[15] 张元元,陈光淦. 带Robin边界条件的2维随机Ginzburg-Landau方程的吸引子[J]. 四川师范大学学报(自然科学版),2015,38(1):20-26.

2010 MSC：35B41; 35Q35

(编辑 李德华)

The Uniform Boundedness and Convergence of Uniform Attractors for the Non-autonomous Modified Swift-Hohenberg Equations with Singularly Oscillating External Force

LIU Shifang, MA Qiaozhen

(College of Mathematics and Statistics, Northwest Normal University, Lanzhou 730070, Gansu)

In this paper, we consider the non-autonomous modified Swift-Hohenberg equations with singularly oscillating external forceut+△2u+2△u+au+b|u|2+u3=g(x,t)+ε-ρh(t/ε),forρ∈[0,1) andε>0, and the corresponding S-H equationut+△2u+2△u+au+b|u|2+u3=g(x,t),(w.r.t.ε)boundednessoftherelateduniformattractorsAε.Furthermore,theconvergenceoftheattractorsAεofthefirstequationtotheattractorA0ofthesecondoneisprovedasε→0+.

modified Swift-Hohenberg equations; uniform attractor; singularly oscillating external forces; uniform boundedness

2015-03-31

国家自然科学基金(11101334)和甘肃省自然科学基金(1107RJZA223)

O175.29

A

1001-8395(2016)06-0838-05

10.3969/j.issn.1001-8395.2016.06.011

*通信作者简介：马巧珍(1972—),女,教授,主要从事应用微分方程与无穷维动力系统的研究,E-mail:maqzh@nwnu.edu.cn