基于前景理论的应急交通疏散路径选择模型
2016-05-22任其亮
任其亮,曾 柯,王 坤
(重庆交通大学 交通运输学院,重庆 400074)
基于前景理论的应急交通疏散路径选择模型
任其亮,曾 柯,王 坤
(重庆交通大学 交通运输学院,重庆 400074)
为了能够更好地反应在应急交通疏散过程中被疏散者的行为决策反应,引用前景理论中的“有限理性”来描述不确定风险下的应急疏散行为。通过重新定义疏散中的“有效备选路径”这一概念,计算了各“有效备选路径”的前景值,从而确定前景理论值最大的有效备选路径作为应急疏散路径。算例证明了该路径选择结果更符合应急交通疏散下不确定情况的真实路网中的路径选择行为。研究结果对决策者在紧急环境下做出科学、有效的疏散决策具有一定的参考价值。
交通运输工程;应急交通;疏散路径;选择模型;前景理论;有效路径;有限理性
台风、地震等突发事件发生后,需要快速开放受灾区域的相关疏散避难点并对受灾区域的民众进行疏散。随着我国汽车产业蓬勃发展,小汽车在普通家庭普及程度越来越高,一般而言拥有小汽车的家庭在应急疏散中更加倾向于驾驶自家车辆。由于外界环境、个人心理特征等影响因素,被疏散者具有不同的出行决策行为,如果没有充分考虑到疏散民众的出行决策行为的异同,可能会导致疏散过程中发生供需不均衡的情况,使某些疏散道路发生堵塞。目前对于交通疏散路径选择行为大多是在一般的交通状态下进行研究的,主要采用的方法为期望效用理论以及随机效用理论,针对应急状态下的疏散路径选择的研究也为数尚少。现有研究主要有:陈林[1]运用改善后的SP (stated preference)调查与Logit模型对成渝通道交通选择的行为进行了研究;刘海洋[2]在调查问卷收集的数据的基础上采用多项Logit模型和Nested Logit模型通过建模分析了出行者的出行选择行为;武小康等[3]对应急交通疏散中被疏散者的疏散终点选择行为与疏散路径选择行为进行了综合分析与研究,分别建立了树状组对Logit、二项Logit模型用来描述应急交通疏散中被疏散者的疏散行为。
以上研究均假定所有决策者都是“完全理性人”,并且决策者总是追求效用最大化。但是在应急交通状态下,交通环境复杂,出行者的心理也会因此产生恐慌等不利的情绪。继续运用期望效用等理论预测出来的结论与紧急疏散中人们的实际表现行为肯定有较大差异。因此,应急交通疏散下的路径选择问题就是一种不确定风险下的路径选择。笔者拟运用前景理论对应急状态下出行者的驾驶路径选择行为进行分析,最终得到基于前景理论的应急交通疏散路径选择模型。
1 应急状态下路径选择行为分析
应急交通疏散中,被疏散者的路径选择行为及疏散者的路径决策均受到诸如年龄组成、性别组成、文化程度、职业、兴趣爱好、性格以及过往经历等多因素的影响。结合以往学者的研究,在应急交通状态中,最容易产生的是心理恐慌状态,在恐慌状态下,不同的人有不同的反应。比如有的人员经历过类似场景或者具备良好的心理素质等等,往往表现为适应性的行为;相反,有的出行者会由于恐慌产生一些非适应性的行为。何健飞[4],林姚宇等[5]在其研究中认为,恐慌将会导致出行者的判断力下降,因此会导致盲目地从众行为是恐慌状态下最主要的行为表现。考虑到应急状态下人员心理行为的复杂性,同时为保障研究结果对于应急交通疏散具有一定的参考意义。笔者定义被疏散者既不是“完全理性”也不是“完全非理性”,而属于“有限理性”的人群。
应急疏散中,最快的离开危险源并到达安全的避难场所是疏散人群选择应急疏散路径的最主要依据[6]。由于在应急交通状态下的路径选择属于多种不确定因素共存的路径选择状态,因此笔者借鉴前景理论来分析这种应急状态下的路径选择行为。首先建立以车辆应急交通疏散的预测时间为参照点作为被疏散者选择疏散路径的基础。然后通过以参照点为基础的价值函数确定每条备选路径的价值以及选择概率。最后通过前景值计算模型计算出每条备选路径的前景值,从而选取前景值最大的路径作为应急交通疏散路径。
2 应急交通疏散路径选择模型
2.1 变量定义
变量定义如下:

2.2 备选路径的选择
为解决实际路网中路径全集计算复杂的问题,引进改进后的“有效备选路径”[7]来定义备选路径,备选路径应满足以下3个条件:
1)路径k为无环的简单路径[8];

3)路径k的路段(i,j)必须满足s(i)>s(j),s(i)为节点i至终点s的最小阻抗值。根据此定义,备选路径的具体求解步骤如下:
步骤1:计算从疏散点r到达其它所有节点的最小时间,即确定 r(i),计算从避难点s到达其它所有节点的最小时间,即确定 s(j);找出疏散点到避难点的所有无环简单路径,同时算出其阻抗。
步骤2:判断步骤1得到的路径k是否满足阻抗处在最短路径阻抗的(1+Hr,s)倍之内。
步骤3:判断路径k是否属于备选路径,即判断路径k中路段(i,j)是否满足s(i)>s(j),若满足则该路段属于备选路径,否则不属于备选路径。
2.3 参照点设定
前景理论应用过程中,参照点的设定是衡量用户得失的重要标准,在出行者路径选择模型也不例外。一般情况下,出行者在出发之前,为了能够按时到达目的地,会预留一定的出行时间。在应急交通疏散中,被疏散者在高度紧张的状态下,希望用最短的出行时间离开危险区,其疏散时间受出行目的以及OD(origin-destination)对之间交通状况的影响。传统的参照点设定方法采用所有备选路径自由流时间的加权平均并考虑出行目的来确定参照点:
(1)
针对应急交通疏散的特点,笔者选择预测疏散时间代替自由流时间来设置参照点。于德新等[10]在其研究中描述了车辆应急交通疏散时间的预测模型,假设ρ为疏散时间可靠性,那么应急交通疏散出行者的疏散时间预测模型为
(2)

(3)
式中:p为w中备选路径的总数;β为与出行目的相关的时间价值系数,β∈(0,1),β值越小,表示时间价值越高,β值越大,表示时间价值越低。
2.4 价值函数和决策函数的确定
2.4.1 价值函数

(4)
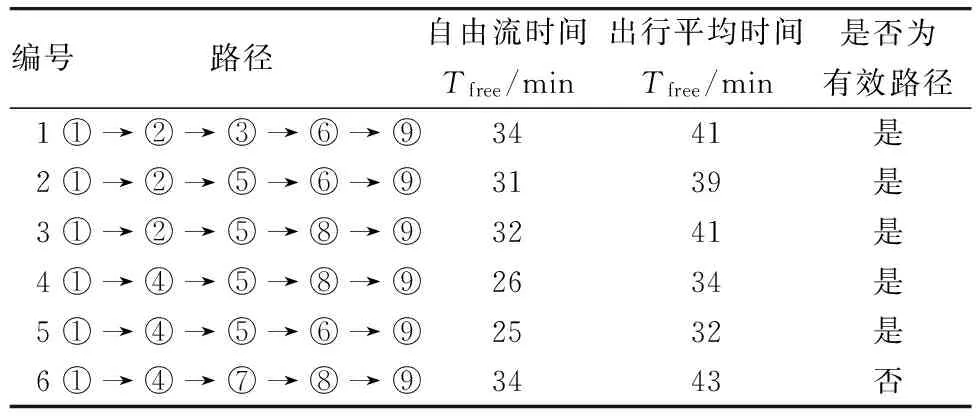
式中:γ为敏感性递减系数,越接近参照点,被疏散者对价值更为敏感;A为收益追求系数;B为损失厌恶系数,0 D.KAHNEMAN等[11]通过实验标定,取γ=0.88,A=1,B=2.25。 2.4.2 决策权重函数 D.KAHNEMAN等[11]认为,概率权重是决策者根据事件结果出现的概率P做出的某种主观判断,是概率发生的一个权重。他们认为概率权重函数π(P)一般应具有以下性质:首先,π(P)是关于概率 P 的单调递增函数,而且在0和1处均不连续。其次,它始终对小概率赋予过大的权重值,即π(P )>P;而对大概率赋予过小权重值,即π(P ) 图1 “前景理论”概率权重函数曲线Fig.1 “Prospect theory” probability weighting function curve 为消除某些技术的不一致性, A.TVERSKY等[12]做了微小的调整:首先,假设使用累积分布函数作为权重的基础;其次,提出一个修正的权重函数为 (5) (6) 假设在应急疏散过程中,疏散路网中的路段互不干扰,相互独立,则可以认为路段的行程时间也是相互独立的。因而从疏散点到避难点的每一条路径包含的路段行程时间就构成了一个独立的随机变量序列。根据中心极限定理可知,路径的行程时间将近似符合正态分布,即 (7) (8) (9) 2.5 计算备选路径前景值 (10) 2.6 路径选择模型 由2.2小节假设可知,w中的应急交通备选路径总数为p,选取的路径k必为这p备选条路径中前景值最大的路径,即路径k应该满足 (11) 图中节点1为应急疏散点,节点9为应急避难点,设定θ=0.3。根据2.3小节分析,在应急交通疏散中,由于出行者心理因素的影响,其可靠性需求ρ取值应该大于0.5,笔者取ρ=0.6,β=0.4。 图2 测试路网Fig.2 Test road network 根据2.2小节备选路径的选取原则,选取“有效备选路径”如表1。 表1 有效路径选择表 根据式(2)~式(10)及相关参数的设定,可分别计算从疏散点1到避难点9之间5条备选路径前景值。计算情况如表2。 表2 前景值计算表 由表2可知,有效路径为路径5(①→④→⑤→ ⑥→⑨),其前景值为 因此,路径5(①→④→⑤→⑥→⑨)即为该路网从应急疏散点①出发到达应急避难点 ⑨的最佳可选路径,即出行者将选择路径5 出行。 将该结果放回到测试网络中可以看出,路径 5 经过的路段具有较小的自由流时间和路段出行时间均值。更重要的是,与其他几条“有效路径”相比,路径5路段的出行平均时间值与自由流时间的差值均较小,说明这些路段的路况较其他路段更为稳定,即通过路径5进行应急疏散时,在预期疏散时间内到达疏散点的可能性更大。 借用不确定风险下的行为决策理论“前景理论”对应急交通疏散的出行者的路径选择决策行为进行了分析,以疏散预测时间为参照点代替了传统的前景理论的参照点,建立了相应的应急交通疏散路径选择模型。通过算例计算得出前景理论提出的心理账户及主观概率,以人们的“有限理性”为前提,更符合出行者路径选择行为的描述。 笔者研究仍存在如下需要进一步考虑和研究的问题: 1)假设在应急交通疏散中出行者均为“有限理性”,但是不排除有小部分的“非理性”行为,下一步应考虑将这一部分群体考虑到路径的选择决策模型中。 2)假设的应急交通疏散路径的选择是在应急疏散前就做好选择,并没有考虑到由于出行者以及外界环境的影响下中途决策的改变,今后应继续探讨在应急交通疏散中的变参照点的问题。 3)笔者运用的前景理论中的相关参数值均采用的原始理论中标定的参数值。对于应急交通的特殊状态,下一步可以采取问卷调查的方式,针对应急交通疏散的特点,重新对前景理论中的公式进行标定,并用重新标定的路径选择模型来进行实例验证。 [1] 陈林.基于Logit模型的成渝通道交通选择行为研究[D].成都:西南交通大学,2013. CHEN Lin.AnalysistheCorridorTrafficChoiceBehaviorBetweenChengduandChongqingBasedonLogitModel[D].Chengdu: Southwest Jiaotong University,2013. [2] 刘海洋.基于Multi-Agent的交通应急疏散终点与路径选择行为仿真研究[D].哈尔滨:哈尔滨工业大学,2011. LIU Haiyang.DestinationandRouteChoiceofTrafficEmergencyEvacuationBasedonMulti-AgentSimulation[D].Harbin: Harbin Institute of Technology,2011. [3] 武小康,周利锋.行人仿真在轻轨车站应急疏散领域的应用[J]. 重庆交通大学学报(自然科学版),2012,31(4):772-776. WU Xiaokang,ZHOU Lifeng. Application of pedestrian simulation software on the emergency evacuation at light rail station[J].JournalofChongqingJiaotongUniversity(NaturalScience),2012,31(4):772-776. [4] 何健飞.基于行为的应急疏散路径优化与仿真[D].上海:上海交通大学,2013. HE Jianfei.AnEmergencyEvacuationRoutingOptimizationandSimulationBasedonBehavior[D].Shanghai:Shanghai Jiaotong University,2013. [5] 林姚宇,丁川,吴昌广,等.城市高密度住区居民应急疏散行为研究[J].规划师,2013,29(7):105-109. LIN Yaoyu, DING Chuan,WU Changguang,et al. Analysis on high density community emergency evacuation behavior[J].Planners,2013,29(7):105-109. [6] 任其亮,乔丹.灾后应急救援运输路径优化模型研究[J]. 重庆交通大学学报(自然科学版),2010,29(6):951-954. REN Qiliang,QIAO Dan. Emergency rescue traffic route optimization model after disaster[J].JournalofChongqingJiaotongUniversity(NaturalScience),2010,29(6):951-954. [7] 秦民,姜培.基于有效路径的多路径交通流分配[J].交通标准化,2010,34(9):30-33. QIN Min,JIANG Pei.Multi-path traffic assignment based on effective paths[J].TransportStandardization,2010,34(9):30-33. [8] 李志纯,黄海军.随机交通分配中有效路径的确定方法[J]. 交通运输系统工程与信息,2003,3(1) :28-32. LI Zhichun,HUANG Haijun. Determining the efficient paths in stochastic traffic assignment [J].JournalofTrafficSystemsEngineeringandInformationTechnology,2003,3(1):28-32. [9] LEURENT F M. Curbing the computational difficulty of the logit equilibrium assignment model [J].TrafficResearchB,1997,31(4):315-326. [10] 于德新,仝倩,杨兆升,等.重大灾害条件应急交通疏散时间预测模型[J].吉林大学学报(工学版),2013,43(3):654-658. YU Dexin,TONG Qian,YANG Zhaosheng, et al. Forecast model of emergency traffic evacuation time under major disaster[J].JournalofJilinUniversity(EngineeringandTechnologyEdition),2013,43(3):654-658. [11] KAHNEMAN D,TVERSKY A. Prospect theory:an analysis of decisions under risk[J].Econometric,1979,47(2):313-327. [12] TVERSKY A,KAHNEMAN D. Advances in prospect theory:cumulative representation of uncertainty[J].JournalofRiskandUncertainty,1992,5(4):297-323. [13] 王任映.基于前景理论的出行路径选择模型[D].长沙:长沙理工大学,2009. WANG Renying.StudyofRouteChoiceModelBasedonProspectTheory[D].Changsha:Changsha University of Science and Technology,2009. Model of Evacuation Route Choice in Emergency Traffic Based on Prospect Theory REN Qiliang, ZENG Ke, WANG Kun (School of Traffic & Transportation, Chongqing Jiaotong University, Chongqing 400074, P.R.China) In order to better reflect the true response of evacuees’ decision in emergency evacuation, “bounded rationality” in prospect theory was used to describe the evacuation behavior of the person under uncertain risk. The emergency evacuation routing which had the maximum prospect value was determined by redefining the concept of “effective alternative path” and calculating the prospect values of various effective alternative paths. Through an example of emergency evacuation, it is indicated that the result of the above route choice is more in line with the route choice behavior in the real road network under the uncertain conditions of emergency traffic evacuation. The research result is of certain referential value for the decision makers under emergency circumstances to make scientific and effective evacuation decision. traffic and transportation engineering; emergency traffic; evacuation route; choice model; prospect theory; effective path; bounded rationality 10.3969/j.issn.1674-0696.2016.03.21 2014-07-21; 2015-01-12 重庆市科委基础与前沿研究项目(cstc2014jcyJA70028);重庆市教委自然科学研究项目(KJ130422) 任其亮(1978—), 男,山东莱芜人,教授,博士后,主要从事交通规划、交通安全及智能交通方面的研究。E-mail:cqrql@126.com。 曾 柯(1991—),男,湖北黄冈人,硕士研究生,主要从事交通规划、交通安全及智能交通方面的研究。E-mail:Zengwuji2010@sina.com。 U491 A 1674-0696(2016)03-100-05






3 算例分析



4 结 语
