计及计划内偏差和风速分布的风电场商日前市场竞标研究

江岳文, 林小雨

(福州大学电气工程与自动化学院， 福建 福州 350116)

计及计划内偏差和风速分布的风电场商日前市场竞标研究

江岳文, 林小雨

(福州大学电气工程与自动化学院， 福建 福州 350116)

随着大规模风电并网和电力市场的发展，风电场商被要求参与到电力市场中。由于风电的波动性和不可准确预测性，风电场商在竞标出力获取收益的同时，需要承担无法准确申报出力而导致的不平衡费用。本文遵循风电本身的客观规律，提出不平衡费用的收取需要考虑功率计划内偏差，详细推导在风电场风速满足威布尔分布情况下的风电场商日前市场竞标模型，该模型以风电场商期望收益最大化为目标，在日前市场风电场商获得竞标出力收入，在不平衡市场风电场商收取超过计划内偏差功率部分的不平衡费用。算例详细分析不平衡市场的报价、计划内偏差比例和不同风速分布参数对风电场商日前市场竞标出力的影响。

风电场商； 日前市场； 投标策略； 计划内偏差

1 引言

截止到2013年底，全球风电装机容量累计达到 31813.7万kW，从2009～2013 年的五年中，全球风电市场的规模几乎增长了 2 亿kW[1]。2013年，中国新增风电机组 9356 台， 新增装机容量16088.7MW，同比增长24.1%；累计安装风电机组达到 63120台，装机容量为91412.89MW，同比增长21.4%。新增和累计装机容量均为世界第一[2]。目前，为了鼓励风电的继续发展，电网采取全额收购风电的有效出力。但随着风电水平的增加，由于风电的波动性、不可准确预测性及间歇性等特点，电网为了全额接纳风电需要付出较大的经济代价，需要更多的旋转备用、调峰成本和AGC成本[3,4]。这些加重了电网和常规电源辅助服务的负担。因此，电力系统在鼓励风电发展的同时，也提出让风电场商与常规能源投资商一样参与市场，让风电承担一定的功率不平衡费用[5-7]。

由于风电场商需要承担一定的不平衡费用，使得风电场商的收益有所损失。根据英国、西班牙等国风电市场统计，其损失的收益达到总收益的10%[8]。风电场商为了获取最大利益，需要在日前市场上申报出力时进行策略决策，使得其在日前市场和不平衡市场上的收益之和最大化。为了确定风电场商在日前市场上申报出力的策略，文献[9,10]考虑风电预测精度随时间尺度的缩短而提高的特点，设计了风电日内市场，并在日内市场更新一次日前市场申报的出力，以提高风电场商的收益，减少由于预测不准确所带来的功率不平衡损失费用。风电场商在电力市场上追求自身收益最大化的同时必然也承担着由于风电的不确定性而带来的风险，如何把参与者愿意承担的风险和收益结合起来进行评估，是风电场商策略申报出力所关注的一个内容[11-13]。为了进一步减少风功率偏差，文献[14,15]将风能和适当容量的储能设施结合起来进行市场投标，以获取更高的利益。由于日前市场和不平衡市场中的价格直接影响到风电场商的收益，因此，文献[16]详细分析了不平衡市场中买入和卖出价格的变化对收益的影响。

文献[9-16]都考虑了风电难以准确预测引起的风电偏差成本，但都未考虑由于风速的特性而使得偏差是客观存在，需要接纳一定的计划内偏差。电网应该接受计划内偏差，即通过不断改进预测手段等措施仍然无法减小的那部分偏差。当日前市场申报的出力和风电场实际出力的偏差在允许范围内时应该不计及风电场商的不平衡费用；只有超过了该允许范畴的功率偏差才收取不平衡费用。本文基于此理念，研究风电场商在日前市场上的竞标策略。

2 风功率与电力市场

2.1 风电场出力研究

风速是一个随机变量，对大量实测数据的长期统计表明，风速的随机分布近似服从 Weibull 函数。其概率密度函数为：

(1)

式中,k为形状系数；c为所描述地区的平均风速;v为风电场的风速(m/s)。设风电场的出力可以用式(2)获得[17]：

(2)

式中,pW、PWN、v、vin、vr、vout分别为风电场的出力、额定出力、实际风速、切入风速、额定风速和切出风速。

根据式(1)和式(2)可得风电场风电出力的概率密度函数为：

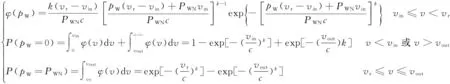
(3)

2.2 风电场商参与市场描述

日前市场制定次日的机组组合方案和功率分配计划，由于天气、网架故障和负荷突变等因素，当日前市场的计划与实际负荷出现较大的偏差时产生不平衡市场。在日前市场，风电场商根据短期风电预测结果或其它竞标策略申报出力与价格。目前，为了节能减排，电网公司全额收购风电，因此可以假设风电场商在日前市场上的报价为零，即风电场商是日前市场出清价的接受者，电网公司在日前市场上采用统一的出清价与发电商和风电场商结算。

由于风电的不能准确预测性，风电场商在日前市场申报的出力与交易日风电场的实际出力肯定是不一致的，由此产生了功率的不平衡。由于风电出力加大了不平衡市场功率的不平衡，系统运行员需要付出更多的经济成本和可靠性成本维持系统的平衡，更多的AGC和旋转备用被调用，这部分新增的辅助服务费用需要风电场商支出。但由于风电出力的客观属性，把所有不平衡的风电功率放在不平衡市场中接受惩罚对风电场商是不公平的。客观来讲，风电出力的偏差可以缩小，但无法消除。鉴于此，本文考虑放宽对不平衡功率的定义，允许适度的功率偏差存在，将其作为不惩罚的不平衡功率。系统运行员可以根据本电网风电场运行特性、风功率预测水平和系统辅助服务提供情况确定一个计划内偏差比例，当然这个比例随着风电预测技术的提高可以逐渐缩小。现在由于风电出力短期预测精度只能达到80%左右[18]，该计划内偏差比例可以设置在10%～15%左右。一方面促进风电场商努力提高出力预测技术，尽量减小出力偏差；另一方面，也体现了电力市场对自然规律的尊重。

在不平衡市场中，当风电场商申报出力比实际出力小，则会产生多余风功率，风电场商可以在不平衡市场上卖出多余功率；当风电场商申报的出力较大时，风电场商需要在不平衡市场购买不足的功率。

为了促进风电场商尽量准确地在日前市场上提供功率，一般来讲市场的价格满足ρbuy,t≥ρt≥ρsell,t≥0，其中，ρsell,t为t时段不平衡市场上风电场商出售多余功率的价格；ρbuy,t为t时段不平衡市场上风电场商购买不足功率的价格；ρt为日前市场t时段市场清算价。

3 风电场商日前市场竞标策略

日前市场上风电场的出力按照风电场商申报出力进行结算，其他超过计划内偏差的不平衡功率则在不平衡市场中进行结算。由于含有风电出力这一随机变量，因此，风电场商收益的目标函数为一期望值：

(4)

式中，E(R)为风电场商期望的收益；N表示日前市场的时段数，一般为24h，故公式中省略了时间分量；NBup,t表示由于日前市场申报出力较少，超过了计划内偏差，多余出力在不平衡市场上出售而获得的收益；NBunder,t表示由于日前市场申报出力较多，超过了计划内偏差，在不平衡市场上购买欠缺功率而失去的收益；Pw,t为风电场商在日前市场t时段申报的出力，为决策变量。

式(4)中第二部分NBup,t代表多余出力在不平衡市场上出卖而获得的收益，即：

(5)

式中，α为计划内的风电出力偏差比例。

式(5)可以进一步转化为：

(6)

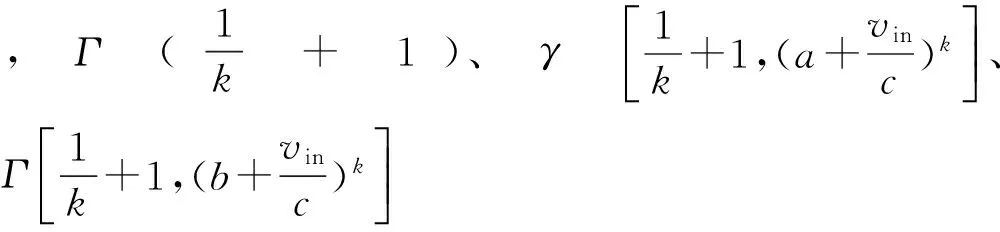
式(4)中第三部分NBunder,t代表风电场商在不平衡市场上购买欠缺功率而失去的收益，即：

(7)

式(7)可以进一步转化为:

(8)

式中

由于电价的分布很难用一个具体的分布函数来描述，网架结构和负荷水平不同，分布规律都有差异，因此文中直接采用确定的日前市场电价结果作为风电场商申报出力的决策依据。

该模型虽然涉及到多个时段，但由于风电场商收益的最大化主要依赖该时段风电场出力，而风电场各时段出力可以认为是彼此独立的量，因此问题的求解可以解耦到每个小时，即一天收益的最大化必然由每个小时收益的最大化得到[19]。

4 算例研究

某风电场参数：PWN=50MW，vin=3m/s，vr=15m/s，vout=25m/s。该风电场风能预测数据满足Weibull分布，利用极大似然法得出Weibull分布参数k=1.7627，c=6.2609。以0时段为例，短期预测出力值为10.25MW，日前市场出清电价ρt为S | 44.59/(MW·h)。采用粒子群优化算法进行求解分析。

(1)计划内偏差比例、不平衡市场报价对日前市场竞标出力和收益的影响

算例分析了四种不平衡市场的报价模式：①满足本文设定ρbuy,t≥ρt≥ρsell,t≥0的第1种报价模式，假设ρsell,t=0.6ρt，ρbuy,t=1.4ρt；②第2种报价模式，不平衡市场出售多余功率的价格为0，购买不平衡功率的价格大于日前市场的清算价，假设ρsell,t=0，ρbuy,t=1.4ρt；③第3种报价模式，不平衡市场上购买欠缺功率的价格为0，出售多余功率的价格小于日前市场清算价，假设ρsell,t=0.6ρt，ρbuy,t=0；④第4种报价模式，不平衡市场上出售多余功率的价格大于日前市场清算价，购买欠缺功率的价格小于日前市场清算价，假设ρsell,t=1.4ρt，ρbuy,t=0.6ρt。

不同计划内偏差和报价模式的竞标出力、风电场商收益分别如图1和图2所示。从图1可以看出，当不平衡市场上为第3种和第4种报价模式，即出售不平衡功率的价格比购买不平衡功率的价格高，风电场的竞标出力始终为风电场的额定出力(50MW)，这是因为此时风电场商不需要承担在不平衡市场上买进缺额功率的义务。可见，这两种不平衡市场定价模式不利于系统功率的平衡，无法为风电场商竞标出力提供合理的价格机制。在相同计划内偏差下，与第2种报价模式相比，第1种报价模式即出售不平衡功率价格低于购买不平衡功率的价格，有着更低的竞标出力和更高的收益。第1种报价模式使得风电场商尽量考虑竞标出力与实际出力接近或略低于实际出力，这样一方面可以减少在不平衡市场上购买出力，另一方面还可以在不平衡市场上适当出售剩余出力而获利；第2种报价模式因为在不平衡市场上出售多余出力无法受益，风电场商必然会适当提高出力竞标，减少弃风电量发生的概率，该竞标策略会增加风电不足概率，需要在不平衡市场上购买缺额功率，从而使得期望收益下降。上述分析也进一步证实了本文设定的报价模式(ρbuy,t≥ρt≥ρsell,t≥0)的合理性。

图1 不同计划内偏差和报价模式的竞标出力Fig.1 Changing of bidding power with allowable deviation and quoted price of imbalance market

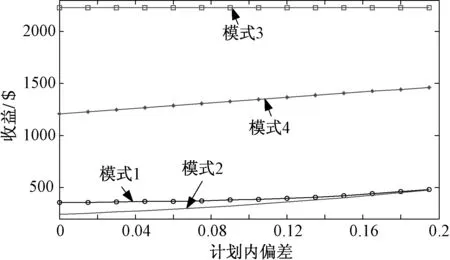
图2 不同计划内偏差和报价模式的风电场商收益Fig.2 Changing of bidding revenue with allowable deviation and quoted price of imbalance market

随着计划内偏差α的增加，由于在不平衡市场上风电场商出卖或购买功率减少，在日前市场上风电场商收益增加。如图1和图2所示，在不平衡市场不同的定价水平下，当ρbuy,t不为0时，随着计划内偏差α的增大，风电场商竞标出力逐渐增加，风电场收益也随之逐渐增加。以第1种报价模式为例，在同样的风资源下，α=0时的最佳竞标出力为8.6893MW，而α=0.2时，则最佳竞标出力达到32.3574MW，收益从S|355.9038增加到S|482.9602。可见，计划内偏差比例的变化对风电场商收益产生了直接的影响。图3表示第1种报价模式下最佳竞标出力和不平衡市场上的偏差出力随计划内偏差的变化趋势。

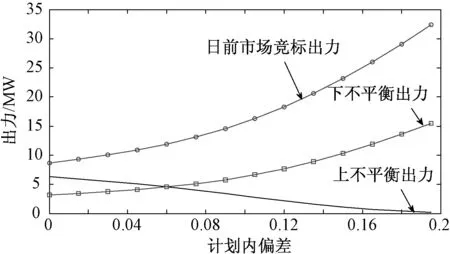
图3 不同计划内偏差的竞标出力及不平衡功率Fig.3 Changing of bidding power and imbalance power with allowable deviation

(2)计划内偏差比例和风资源对日前市场申报出力和收益的影响

图4和图5分别表示竞标出力和竞标收益与计划内偏差比例α、风速Weibull分布形状参数k的关系。同样的k值水平下，计划内偏差α越大，则风电场商竞标出力越大，且收益也越大。

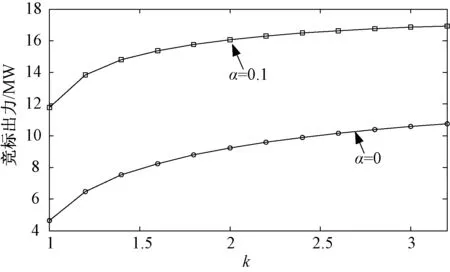
图4 k和α值变化对竞标出力的影响Fig.4 Changing of bidding power with k and α

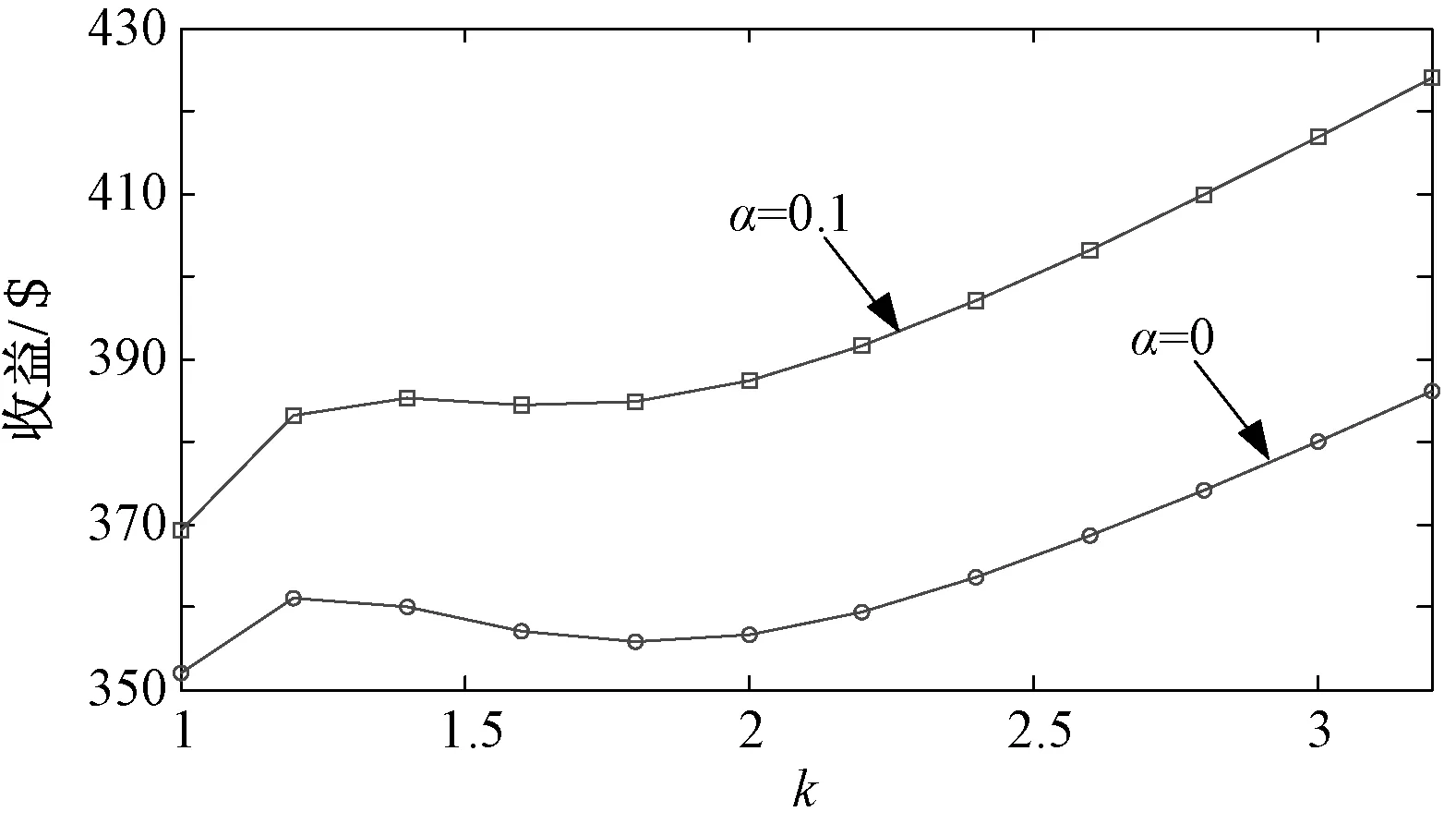
图5 k和α值变化对竞标收益的影响Fig.5 Changing of bidding revenue with k and α

同样的计划内偏差α下，随着k的增加，竞标出力逐渐增大。当c=6.2609m/s时，随着形状系数k的增大，风速的Weibull概率分布密度曲线趋势逐渐变陡，概率最大时风速增加，概率分布密度曲线峰值变大。当风速为6.2606m/s，不管k取图中何值，分布函数的概率均为0.6321。在这一风速前，同样的风速，k越小，分布函数的值越大；在这一风速后，同样的风速，k越大，分布函数的值越大。因此，随着k的增加，大风速出现的概率会增加，小风速出现的概率将减少，从而使得风电出力期望值增加，竞标出力也随之增大，收益总体趋势是随着k的增加而增加。

图6和图7分别表示竞标出力和竞标收益与计划内偏差比例α、风速Weibull分布尺度参数c的关系。同样的c值水平下，计划内偏差α越大，则风电场商竞标出力越大，且收益也越大。

图6 c和α值变化对竞标出力的影响Fig.6 Changing of bidding power with c and α

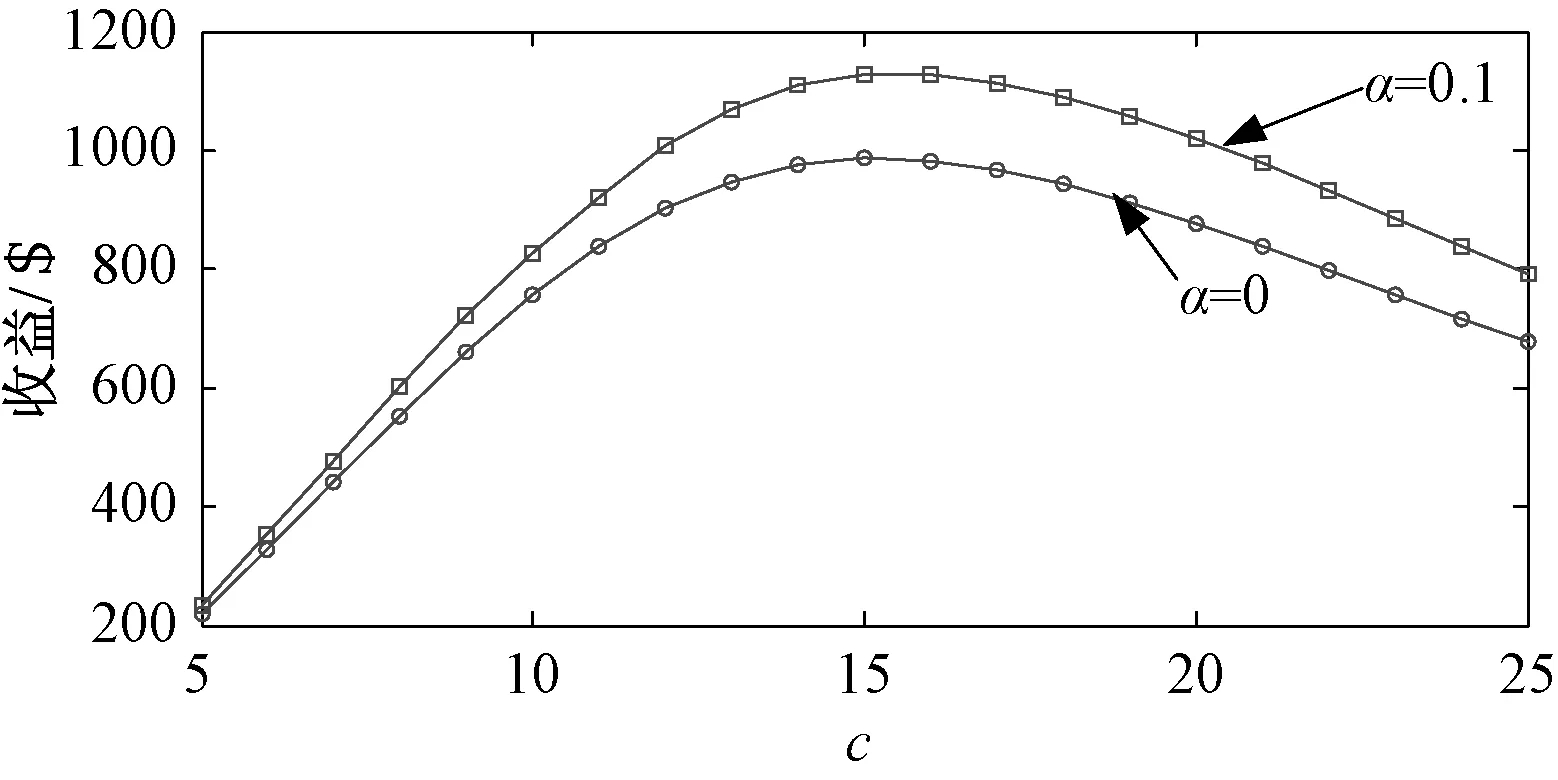
图7 c和α值变化对竞标收益的影响Fig.7 Changing of bidding revenue with c and α

在计划内偏差α=0时，随着c的增加，竞标出力逐渐增大。当k=1.7627，随着尺度系数c的增大，风电的竞标出力和收益都逐渐下降。随着c的增加，风速的概率分布密度曲线趋势逐渐变缓，概率最大时出现的风速变大，密度曲线峰值减小。大风速出现的概率逐渐增大，小风速出现的概率逐渐减少。概率分布曲线随着c的增加，也逐渐变平稳。因此，随着c的增加，风电场期望出力将增大，故竞标出力增大。但当c大于17m/s时，此时切除风速(大于25m/s)概率增加，发电出力期望值反而减少，所有竞标出力和收益会下降。

当α=0.1时，随着c的增加，竞标出力逐渐增大，直至11m/s时风电竞标出力达到50MW；在c=16m/s时，由于切除风速概率增加，期望出力减小，收益水平开始下降。

5 结论

随着风电大规模的发展，风电参与市场交易是必然的趋势。由于风电的波动性及不可准确预测性，风电不可能完全像常规能源市场一样参与竞争。本文提出了考虑风电波动的计划内偏差竞标策略模型，并对算例进行详细分析，具体结论如下。

(1)风电参与市场竞标，需要适当放宽其申报出力的准确度，即计划内偏差，该偏差水平可以根据风速预测精度等因素适当调整。

(2)当日前市场申报的出力与实际风电出力偏差超过计划内偏差时，才会产生不平衡功率。风电场商需要在不平衡市场卖出或买入不平衡功率，产生的不平衡费用降低了风电场商的收益。因此，风电场商会尽量提高风电预测技术，提高出力申报的准确性，增加自身收益。

(3)随着计划内偏差比例水平的增加，不论不平衡市场的报价如何，风电场商的竞标出力和收益都不会减少。

(4)反映风资源分布的形状参数k和尺度参数c的变化将引起风电竞标出力和竞标收益的变化。随着k增加以及计划内偏差比例的增大，竞标出力和收益都有上升的趋势；随着c增加以及计划内偏差比例的增大，竞标出力先随着c的增大而增大并达到峰值(α较大，则稳定在风电场额定出力处)后减小，竞标收益也存在同样的规律。

附录

式(5)至式(6)的推导过程如下：

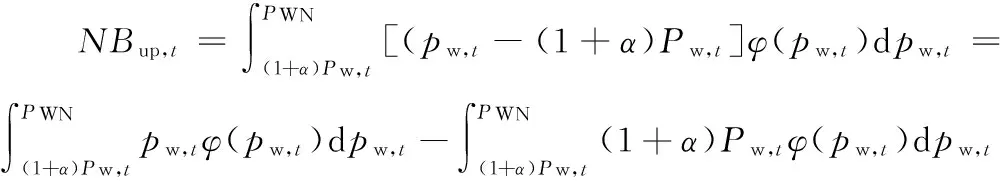
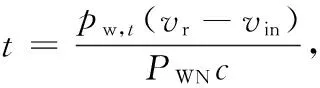
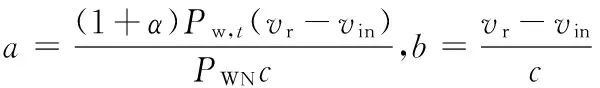
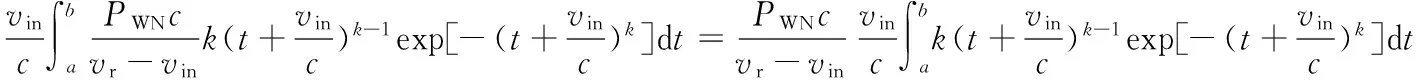
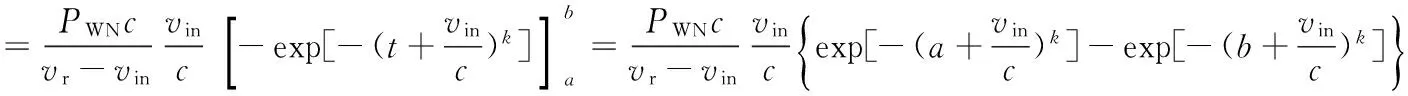
所以

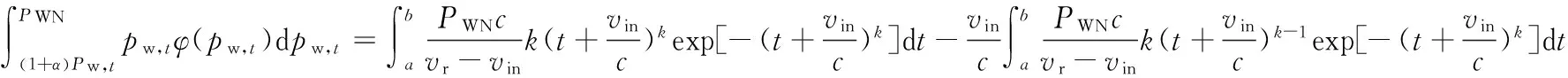
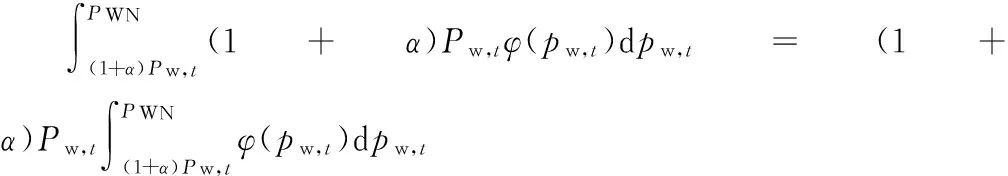
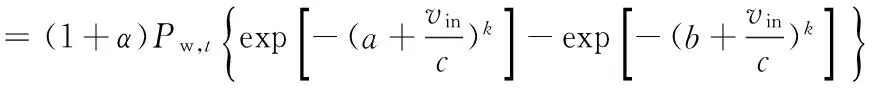
在额定功率上的概率为：

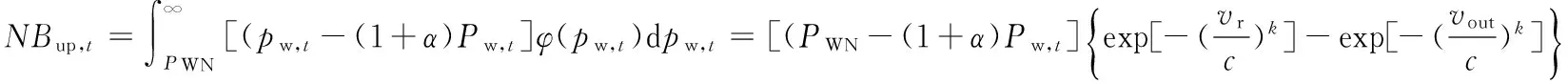
所以

式(7)至式(8)的推导过程与以上部分类似，不再赘述。

[1] 全球风能理事会 (Global Wind Energy Council). 2013全球风电统计 (The 2013 global wind power statistics) [J]. 风能 (Wind Energy)，2014, (2): 60-63.

[2] 中国风能协会 (Wind Energy Association of China). 2013年中国风电装机容量统计 (Chinese wind power installed capacity in 2013) [J]. 风能 (Wind Energy)，2014, (2): 44-55.

[3] 吴政球, 王韬 (Wu Zhengqiu, Wang Tao). 风电功率预测偏差管理与申报出力决策 (Deviation management of wind power prediction and decision-making of wind power bidding) [J]. 电网技术 (Power System Technology)，2011, 35(12)：160-163.

[4] 张宁宇, 高山, 赵欣 (Zhang Ningyu, Gao Shan, Zhao Xin). 一种考虑风电随机性的机组组合模型及其算法(An unit commitment model and algorithm with randomness of wind power) [J].电工技术学报 (Transactions of China Electrotechnical Society)，2013, 28(5)：22-29.

[5] Jiaqi Liang, Grijalva S, Harley R G. Increased wind revenue and system security by trading wind power in energy and regulation reserve markets [J]. IEEE Transactions on Sustainable Energy, 2011, 2(3): 340-347.

[6] A Botterud, Zhi Zhou, Jianhui Wang, et al. Wind power trading under uncertainty in LMP markets [J]. IEEE Transactions on Power Systems, 2012, 27(2): 894-903.

[7] 曾鸣，李晨，王致杰, 等 (Zeng Ming, Li Chen, Wang Zhijie, et al.). 基于 CVaR 报童模型的风力发电商最优投标策略 (The optimal bid strategy of wind power producer based on CVaR newsboy model) [J]. 电力系统保护与控制 (Power System Protection and Control), 2012, 40(24): 14-20.

[8] Angarita J L, Hernandez C A, Usaola J. Analysis of a wind farm’s revenue in the British and Spanish markets [J]. Energy Policy, 2007, 35, (10): 5051-5059.

[9] Usaola J, Moreno M A. Optimal bidding of wind energy in intraday markets [A]. 6th International Conference on the European Energy Market, EEM 2009 [C]. 2009.1-7.

[11] 张海峰, 吴江, 高峰, 等 (Zhang Haifeng, Wu Jiang, Gao Feng, et al.). 基于机会约束规划的风电商日前市场竞标策略 (Bidding strategy based on chance-constrained programming for wind power producers) [J]. 电力系统自动化 (Automation of Electric Power Systems)，2012, 36(13): 67-71.

[12] Pousinho H M I, Mendes V M F, Catalao J P S. A risk-averse optimization model for trading wind energy in a market environment under uncertainty [J]. Energy, 2011, 36 (8): 4935-4942.

[13] Dukpa A, Duggal I, Venkatesh B, et al. Optimal participation and risk mitigation of wind generators in an electricity market [J]. IET Renewable Power Generation, 2010, 4 (2): 165-175.

[14] Thatte A A, Viassolo D E, Le Xie. Robust bidding strategy for wind power plants and energy storage in electricity markets [A]. 2012 IEEE Power and Energy Society General Meeting [C]. 2012. 1-7.

[15] Thakur T, Goyal S, Gambhir J. Optimisation of imbalance cost for wind power marketibility using hydrogen storage [A]. Joint International Conference on Power System Technology and IEEE Power India Conference [C]. 2008. 1-5.

[16] Bueno M, Moreno M A, Usaola J. Strategic wind energy bidding in adjustment markets [A]. 45th International Universities Power Engineering Conference (UPEC) [C]. 2010. 1-6.

[17] 任博强, 彭鸣鸿,蒋传文,等(Ren Boqiang, Peng Minghong, Jiang Chuanwen，et al.). 计及风电成本的电力系统短期经济调度建模(Short-term economic dispatch of power system modeling considering the cost of wind power) [J].电力系统保护与控制 (Power System Protection and Control), 2010, 38(14): 67-72.

[18] 刘瑞叶，黄磊 (Liu Ruiye, Huang Lei). 基于动态神经网络的风电场输出功率预测 (Wind power forecasting based on dynamic neural networks) [J]. 电力系统自动化 (Automation of Electric Power Systems)，2012, 36(11)：19-22.

[19] E Y Bitar, R Rajagopal, P P Khargonekar, et al. Bringing wind energy to market [J]. IEEE Transactions on Power Systems, 2012, 27(3): 1225-1235.

Bidding strategy based on allowable deviation and speed distribution for wind farm owners

JIANG Yue-wen, LIN Xiao-yu

(College of Electrical Engineering and Automation, Fuzhou University, Fuzhou 350116, China)

With the large-scale development of wind power integrated systems and electricity market, wind farm owners are required to participate in the market. The owners will obtain revenue by bidding in the day-ahead market and bear the cost, which comes from the wind power deviation because of its randomness and forecasting error. Now that the deviation is always existent for wind speed forecast， this paper comes up with the bidding optimization model which allows definite deviation. Based on Weibull distribution for wind speed, this paper deduces the bidding model in detail. The aim of bidding strategy is to maximize the owners’ prot while minimizing the punishment cost. The owners obtain revenue from the day-ahead market by bidding power and will be punished in the imbalance market when the deviation accesses the permit. For different quoted price of imbalance market, allowable deviation and parameters of speed distribution, and bidding strategy are discussed by an example.

wind farm owner; day-ahead market; bidding strategy; allowable deviation

2015-04-18

福建省自然科学基金资助项目 (2013J01176)

江岳文(1977-)， 女， 湖南籍， 副教授， 博士， 研究方向为电力系统优化运行、 电力市场和风电并网运行; 林小雨(1991-)， 女， 福建籍， 硕士研究生， 研究方向为风电并网运行。

TK89

A

1003-3076(2016)04-0035-08